“强基计划”中关于带电体系静电能的计算及其拓展

王 军 邓靖武

(1.北京四中 2.北京教育学院)

静电能,又称为静电势能.带电体系静电能的计算,在“强基计划”中有过考查.分析这一问题前,我们应该先思考:带电体为什么具有静电能? 静电能“储存”(定域)于何处?

对带电体的形成过程,我们可以这样去想象:首先,设想带电体的电荷是由无限多的无穷小部分(dq),按照一定的分布“摆成”的,每一个dq都有自己的位置.在这个带电体形成之前,这些无穷多的、无限小的dq相距无穷远,需要将这些无穷多个dq一个接一个地“放到”带电体上相应的位置处,直至最终形成这个带电体.

有了这个想象过程,我们就能理解,带电体应该具有“静电能”.因为,在按照上述方式形成这个带电体的过程中,必定要克服静电力做功.在这个过程中,克服静电力做的总功,就称为带电体的静电能(或静电势能).同时,也就有了求解带电体静电能的思路.

人们曾经认为带电体的“能量”是储存在“电荷”上的.但是后来研究发现,电磁波(变化的电磁场)可以脱离电荷单独存在,并且电磁波可以携带能量.现在认为,所谓静电能是储存在静电场中的.这种能量和电磁波一样,统称为电磁场能.当然,静电场无法脱离产生它的电荷而单独存在,因此,在处理静电场的电场能时,可以不必在意能量定域于何处.计算带电体能量时,用“电势能”和“电场能”两种观点来计算,结果一致.限于篇幅,本文只从电势能角度分析.

1 点电荷体系的静电能

例1(2018年北大博雅计划)如图1所示,正六边形的边长为R,各个顶点固定有正的点电荷q,中心有负的点电荷2q.求该体系的静电能.

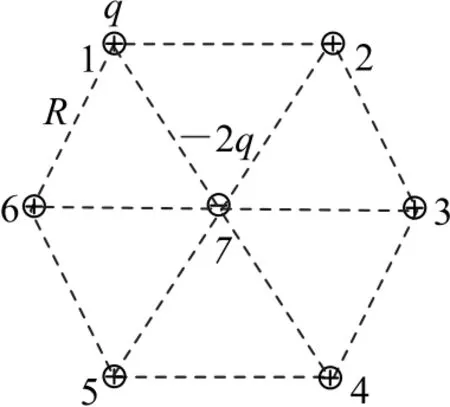
图1

讨论我们用两种观点来计算.

观点1我们设想从无穷远处,按一定的顺序,依次将这7个点电荷放入它们最终的位置.再计算这个过程中,放入每一个点电荷时,需要克服其他已经放置到规定位置的点电荷产生的电场力所做的功,还没有放置于最终位置的点电荷就不用考虑了,这样越到最后放置的点电荷需要克服的静电力做的功就越多.至于按照什么样的次序,依次移入这7个点电荷,是不影响最终结果的,因为“静电势能”只与位置有关.我们选取这样的一种“移入”次序:先移入1号,再移入2号,再依次移入3号、4号、5号、6号、7号.

观点2我们不再去设想移入的次序,而是这样设想:从无穷远将1号移入它的最终位置时,认为其他的所有电荷(2～7号)都已经“就位”,这样移入1号时,需要计算其他所有电荷对1号做的负功.同样的,移入2号时,设想其他所有电荷(1号和3～7号)早已“就位”……对所有7个电荷都进行同样操作.大家可想而知,这样计算的总功一定比“观点1”大了.但是大多少呢? 刚好是“观点1”的2倍.因此,只需要再除以2,就是最终答案了.

“2倍”从何而来呢? 举一个只有三个点电荷的例子来说明.推广到任意个数的点电荷体系也是成立的.

1号移入到最终位置时,根据观点1无电场力做功,将2号移入它的最终位置时,1号的电场力对2号做的功记为－E12,导致体系增加的电势能为E12.依据观点1,则体系总的能量为E＝E12＋E13＋E23.依据“观点2”计算的结果将是E＝E21＋E31＋E12＋E32＋E13＋E23,项数上是前者的2倍,可这还不足以说明后者就是前者的2倍了.还需要证明E12＝E21.两个点电荷间的电势能公式是,自然有E12＝E21.

分析 观点1将1号从无穷远处移入它最终位置的过程中,不需要克服任何电场力做功;将2号移入时,需要克服1号电荷电场力做功,使体系增加的电势能为;将3号移入时,需要克服1号、2号电荷电场力做功,使体系增加的电势能为E13＋;同样的道理,将4号、5号、6号、7号移入时,体系增加的电势能分别如下:

观点2将1号移入时,其他所有电荷已经就位,如图2所示,其他所有电荷在1号位置产生的电势

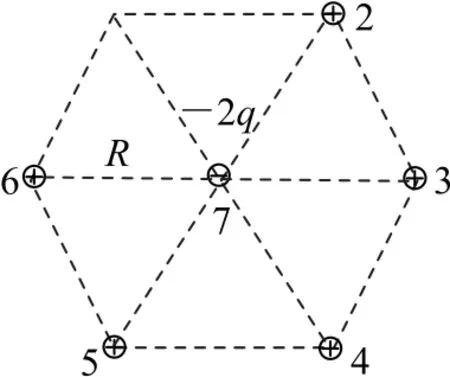
图2

移入1号,体系增加的电势能

考虑对称性,移入2～6号时,体系增加的电势能大小等于E1,移入7 号,体系增加的电势能E7＝,因此,体系总的静电能

2 一个连续带电体的静电能

例2(2021年清华强基计划)如图3所示,半径为R的孤立、均匀带电球体的总电量为Q,求该带电球体的静电能.

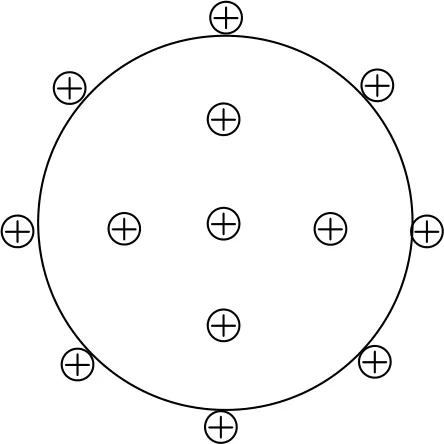
图3

分析 观点1我们设想这样一个过程:如图4 所 示,dq均匀分布在无穷远处的一个“球面”上,然后像肥皂泡收缩一样,汇聚到半径为r的均匀带电球体表面上,使之增加了一个dr的球壳.计算这个过程克服半径为r的均匀带电球体的电场力做的功,就得到了这个过程增加的电势能.对这个过程从0积分至R,就得到了这个均匀带电球体的静电能.半径为r的均匀带电球体的总电量为,其中该球体表面处的电势.

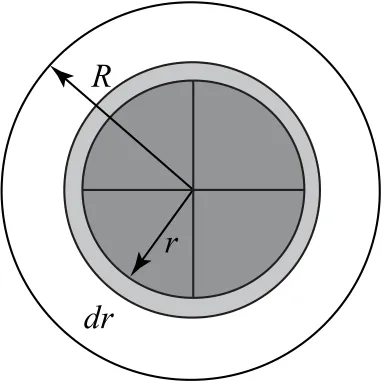
图4

将dq从无穷远处汇聚到该球体表面上的过程中,增加的静电能dE＝φrdq.总的静电能通过对该式积分即可得,过程如下:

观点2从无穷远将电量dq移入它最终位置前,导体上其他所有电荷(Q－dq)均已经就位,因此计算移入dq所增加的静电能时,要解决两个问题:

(1)移入的dq放置在何处?

(2)放置dq的位置的电势是多少?

对于(1),我们仍然想象将dq均匀分布在无穷远处的一个“球面”上,然后像肥皂泡收缩一样,汇聚到半径为r的均匀带电球体表面上.

对于(2),φr将不同于观点1中的结果,因为此时r到R之间,存在早已“就位”的电荷.下面计算φr.

根据高斯定理,可以求出均匀带电球体的场强表达式:

积分计算

因此静电能为

3 拓展:一个带电体和一个点电荷组成系统的静电能

例3如图5所示,一个半径为R的金属球,带电荷量为Q,在距离其球心为d的地方放一个点电荷q,求这个体系的总静电能.

分析本题采用观点2计算较为迅速.下面先用观点2计算,再用观点1计算,通过对比,帮助大家加深理解.

观点2根据观点2,带电导体和点电荷组成的体系的总静电能,其中的φ体 表示带电体的电势,φq表示q所在处的电势.金属球的电势.由于金属球上的电荷分布不均,它在球外点电荷q所在处的电势和场强等于它的镜像电荷所产生的电势和场强.球面上感应电荷的镜像电荷如图6所示.

因此,球面上的感应电荷在球外点电荷q所在处的电势和场强为

方向向右.所以体系总静电能

观点1设想这个带电体系按如下过程形成:先是从无穷远汇聚电荷Q至导体球上,形成一个孤立的均匀带电球体,求出这个过程中增加的能量,这个能量也就是带电量为Q的孤立导体球静电能,记为E1.然后再将q从无穷远处移至距球心为d处,体系又增加了一部分能量,记为E2.

最终形成了题中所述带电体系的总静电能,即有

1)先求孤立导体球静电能E1.

如图7所示,半径为R的孤立导体带电量为Q.

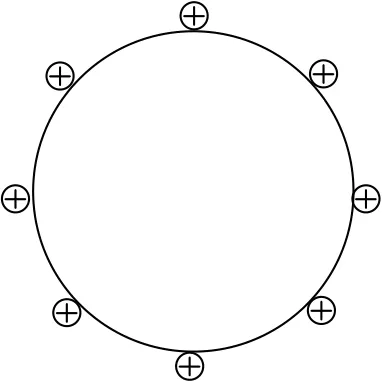
图7

将导体上均匀分布的面电荷分成无数小块的面电荷,电量记为dq.在将dq移入前,导体上均匀分布的面电荷总量为q,在导体球表面产生的电势为φq＝.因此,从无穷远移入dq至导体球表面,使体系增加的能量.积分可得静电能

2)再求将q从无穷远处移至距球心为d处,体系又增加了能量E2.

当点电荷q距离球心为r时,金属球上分布的电荷在r处的电场强度(已经在前面由镜像电荷求出)

方向向右.

将点电荷q沿球的半径－^r方向移动dr,电场力做功

因此从无穷远移动至距离球心为d的过程中,有

因此,将q从无穷远处移至距球心为d处,体系增加的能量

需要注意,在计算E2时,在将q从无穷远处移至距球心为d处的这个过程中,带电金属球上的电荷分布会发生变化,不能认为其上的感应电荷分布一直是最终的那个状态,因此相应的镜像电荷的电量和位置一直是变化的.所以,必须将镜像电荷在距球心为d处产生的电场表达式中的d看成一个变量r.

3)体系总的静电能

这个结果与前面观点2计算出的结果一致.

(完)