声速剖面测量误差对水下定位的影响

李景森, 薛树强, 徐莹, 李保金, 卞加超

(1.中国测绘科学研究院 大地测量与导航定位研究所, 北京 100830; 2.山东科技大学 测绘与空间信息学院, 山东 青岛 266510)

地面和近地空间目标点的位置可由全球导航卫星系统(global navigation satellite system, GNSS)定位技术或北斗定位技术提供,但因为电磁波在海水中衰减严重,因而不能直接用于水下目标点的定位。由于声波可在海水中实现长距离传播的特性,水下目标点的定位通常采用全球导航卫星系统/声学测距组合观测技术(global navigation satellite system-acoustic ranging combination technique, GNSS/A)[1-2]。由GNSS天线确定测量船坐标,再经姿态角和臂长参数通过坐标转换确定换能器坐标,然后测量声信号在换能器与水下目标点的传播时间,最后根据距离交会方法确定水下目标点位置[2]。但由于海水的不均匀特性,导致声线在传播过程中发生弯曲,声速也会随之变化,且声速变化越大,声线弯曲越明显[3-4]。

声速的测量一般分为直接法和间接法。直接法是使用声速测量设备直接测量声速值,如声速剖面仪(sound speed profile, SVP)。由于海水声速主要与海水温度、盐度、深度相关[4-5],其中温度是主要影响因素,深度和盐度次之[6]。通过测量不同深度处的温度、盐度、深度,利用声速经验公式计算声速。测量温盐深的仪器有温盐深测量仪(conductivity-temperature-depth profiler, CTD)、抛弃式温盐深测量仪(expendable conductivity-temperature-depth profiler,XCTD)等设备[7]。周丰年等[8]、陈红霞等[9]、李佳璐等[10]皆对目前的声速经验公式适用范围、精度进行了研究。

受海洋环境的复杂时空变化和声速测量多来源误差影响,声速剖面必然存在测量误差,导致声速测量的不准确。声速误差是影响水下目标点定位的主要因素,其影响大小与声线入射角和传播时间相关[11]。王薪普等[12]、刘以旭等[13]均对顾及声线入射角的水下定位随机模型进行改进和优化。声速误差可细分为2类:一类是声线折射作用引起的误差,目前通常采用等梯度声线跟踪方法予以消除[14-15],即在作业区域内,假设海水介质垂向分层,水平方向无介质变化,且层间声速等梯度变化,根据Snell定律进行逐层解算并累加,但前提是认为整个或局部观测时间窗口内声速结构(sound speed structure, SSS)不发生变化[16];另一类是沿声学信号传播路径的海洋SSS的时空变化[7,17],即由于未实时实地测量声速剖面引起的声速剖面时空代表性误差。其在空间上主要表现为垂向分层结构[4,18],但由于海洋环境的动态变化特性,SSS会随时间发生连续变化,水平方向也会表现为空间异质性[16],且主要体现在海水的浅层;时间上由于受内波、潮汐等影响表现为周期性变化[19-20]。受制于现有声速测量手段,在一定范围内难以实现声速的时空连续监测[21-23]。为了削弱声速剖面代表性误差对定位的影响,现有研究主要通过构建更加精细的三维声速场获得声速分布信息、优化定位模型或增加观测约束等方式削弱误差的影响[17,23]。声速误差的精细化处理是采用GNSS-A方法对海底应答器高精度定位的主要步骤[24]。海底大地基准网的建设同样需要削弱声速误差对海底应答器定位的影响[25-26]。

GNSS-A技术可分为2种实施模式:静态测量[27]和动态测量[28]。在仅考虑声速垂向分层假设的前提下,国外的研究成果主要采用静态测量模式(即测量船位于海底应答器阵列中心的正上方)对海底应答器进行定位,通过优化几何结构,即满足对称的方法,削弱声速误差水平方向分量对定位结果的影响[24];当采用动态测量模式(即测量船沿预设航迹采集声呐观测数据)对海底应答器进行定位,且海面航迹也呈对称结构时,声速误差对海底应答器定位结果的影响为本文的研究内容。

由于声速场是随时空变化的,本文研究仅考虑声速垂向分层假设的前提下,声速剖面观测中产生的误差对海底应答器坐标的影响,包括测量仪器等产生的系统误差及观测偶然误差。

1 声速误差对定位的影响

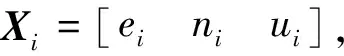
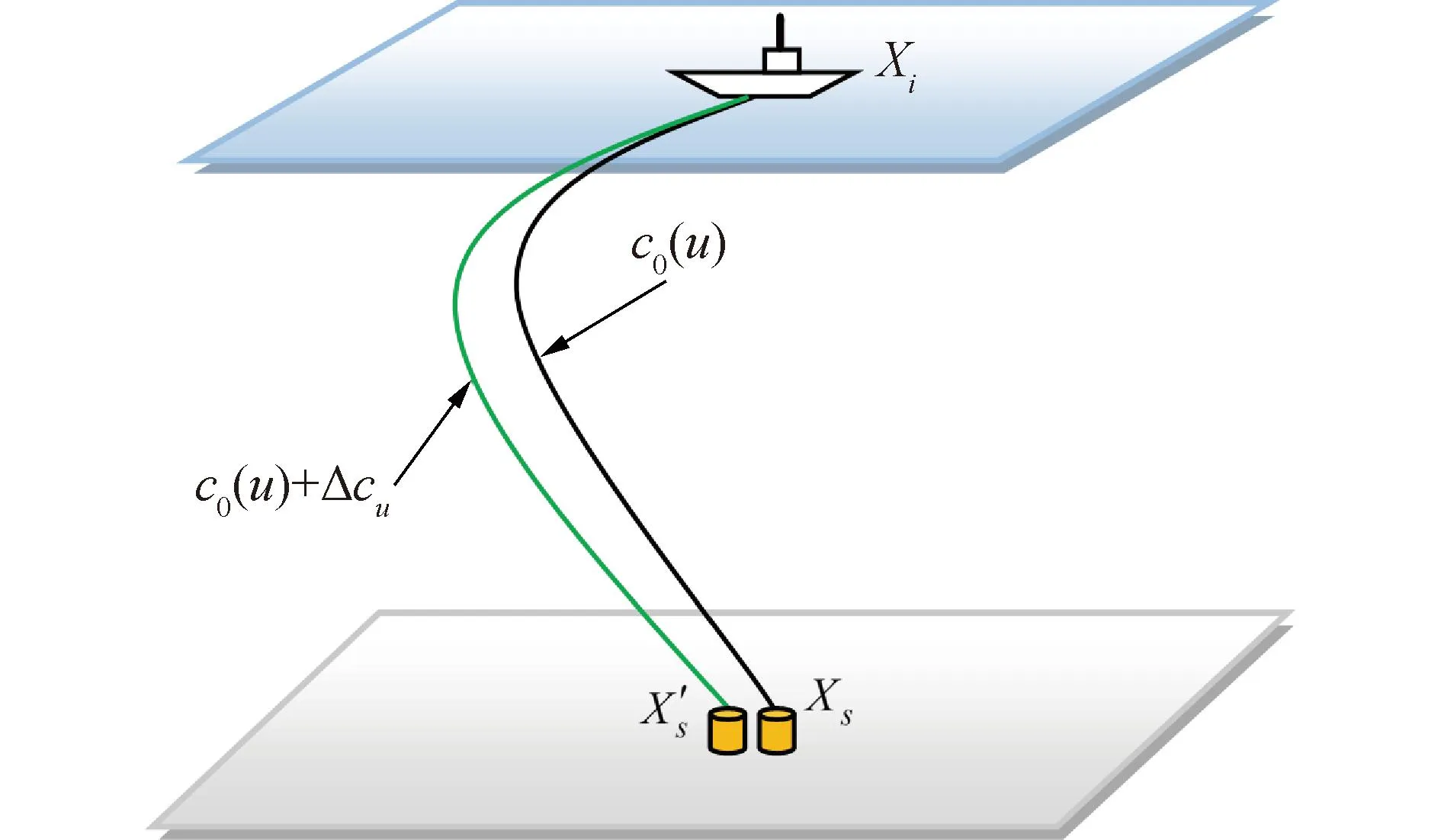
图1 含声速扰动的声速剖面Fig.1 Sound speed profile with sound speed disturbance

针对声速剖面存在声速测量误差的情况,可构建含有声速测量误差的声线跟踪定位模型,即:

(1)

式中:τt为应答器声信号转发的硬件延迟误差,可预先标定,因此在下面的讨论中不考虑此误差;Ti=Tg+Tb为计算得到的往返传播时间;

c(u,Δcu)=c0(u)+Δcu

(2)

式中:c(u,Δcu)为含声速误差影响的声速剖面;c0(u)表示参考声速剖面;Δcu表示在深度为u处引起的声速扰动量。

由于海水存在明显的分层现象,且海水的折射并不会改变声射线的垂直方向,根据Snell定律,单程时间t的计算可通过对每一层积分累加得到[29]:

(3)

式中:α(u)为深度u处的入射角;t=Tg=Tb为往返传播时间Ti的一半[30]。

由式(3)可知,声信号传播时间t随声速c的变化而变化。因而,声速误差通过影响声信号传播时间进而对定位产生影响。

根据泰勒级数展开,保留一阶展开项,可对c-1(u,Δcu)作以下近似:

(4)

则时间t可表示为:

(5)

式中:

(6)

即为声速测量误差对总的传播时间产生的影响。

本文拟采用水下声线跟踪定位算法[31-32](模型1)以及顾及声速剖面时空代表性误差的海底精密定位模型(模型2)对声速误差引起的海底应答器定位精度进行研究。这2种方法的区别在于是否考虑声速剖面的时空变化,前者未考虑,通过射线交会解算海底目标点的三维坐标;而后者将声速剖面的时空变化考虑在内,以3个天顶声学延迟分量作为待估参数来补偿声速的时空变化,通过分段声学延迟估计模型表征其随时间变化的性质。

2 声速误差对定位影响的实验分析

2.1 仿真实验

本文采用仿真程序生成GNSS/声呐观测数据[33],包括声速剖面、发射接收时刻的姿态信息、海面船的发射位置以及接收位置、传播时间信息等。仿真程序初始设置为:海底应答器深度3 000 m,海面正方形边长3 000 m,海底应答器正方形边长1 500 m,观测总时间89.47 h,GNSS天线坐标添加服从正态分布的随机误差(水平方向标准差为0.05 m、高程方向标准差为0.10 m),声速剖面采用经验正交函数(empirical orthogonal function, EOF)内插生成。

海面测量船航迹如图2所示。

图2 仿真海面航迹及海底点分布Fig.2 Simulation of sea track and seafloor point distribution

在上述仿真数据的基础上,分别用模型1和模型2研究声速误差对定位的影响:

方案1:仅对声速剖面添加系统误差,即每一层均加一相同定值,范围为0.1～1 m/s,间隔0.1 m/s。分别用2种模型进行实验,与真值作差,分析其定位结果。

方案2:在仿真数据已生成的基础上,仅对声速剖面的每一层添加均值为零、标准差相同的服从正态分布的随机数,然后通过蒙特卡罗方法对2种模型均实验100次,统计各方向的标准差,分析其定位结果。标准差从0.05 m/s逐渐增加至1 m/s,间隔为0.05 m/s。

2.1.1 方案1:仅对声速剖面添加系统误差

如图3(a)和(b)所示,当海底应答器位于海面航迹的对称轴上,即轴对称时,模型1对海底应答器的定位结果在水平方向上出现了差别,对称轴所对应水平方向上的误差比另一水平方向的误差小2个数量级。如图2和图3(a)所示,当海底应答器M11点位于对称轴(海面航迹关于直线N=0对称)时,M11点的N方向误差比E方向误差小2个数量级;反之,如图2和图3(b)所示,当海底应答器M12点位于对称轴(海面航迹关于直线E=0对称)时,M12点的E方向误差比N方向误差小2个数量级。从这可体现出,海面航迹对称可有效削弱声速剖面系统误差对定位结果的影响。

图3 海底应答器M11、M12以及阵列虚拟中心点与真值的误差Fig.3 Error between the seafloor transponder M11,M12 and the virtual center point of the array and the true value

当采用模型2时,如图3(a)和(b)所示,相对于模型1,模型2的定位误差非常小,水平方向在8 cm以内,甚至在4 mm,高程方向在4 cm以内,能够对声速剖面的系统误差有较大改正。

当对海底基准阵列虚拟中心点定位时,如图2和图3(c)所示,水平方向上的定位误差基本在一个数量级上,并没有产生很大差别,且2种方法的精度基本相当。这也是对称图形可削弱系统误差对定位结果影响的另一验证。当海底应答器位于海面航迹的对称中心时,声速剖面的系统误差对水平方向上影响很小,约厘米级,主要集中在垂直方向。垂直方向的定位误差可通过对定位模型的改进削弱其对定位结果的影响。

2.1.2 方案2:仅对声速剖面添加随机误差

如图4所示,在仅对声速剖面添加服从正态分布的随机数情况下,用蒙特卡罗方法实验100次,并统计各方向的标准差(standard deviation, STD),可以看到,当用模型1定位时,得到的规律与仅对声速剖面加系统误差是一致的,即当海底应答器位于海面航迹的对称轴时,对称轴所对应的水平方向上的误差比另一水平方向的误差小一个数量级,且误差主要集中在垂直方向以及另一水平方向;模型2的规律与2.1.1节的规律是一致的。

图4 海底应答器M11、M12以及阵列虚拟中心点的STDFig.4 The STD of the seafloor transponder M11,M12 and the virtual center point of the array

同样,当海底应答器位于海面航迹对称中心时,水平方向上的定位误差基本在一个数量级上,且2种方法的精度相当。倘若海面航迹图形(航迹点)严格成中心对称且海底点严格位于海面航迹中心位置处,2种方法解算结果在水平方向上会更接近,其对海底应答器水平定位结果的影响也将会更小。不同的是,U方向产生的误差可以通过模型2得到较大改善。

对声速剖面仅添加系统误差以及仅添加随机误差其规律一致,主要是因为在进行计算时,通常采用参考声速剖面代替真实声速剖面,即以参考声速剖面表示这一测量区域的声速剖面,这就导致在进行海底应答器定位时,声速剖面都是相同的,产生的随机误差也会被固定。所以,无论是在声速剖面上仅添加系统误差、仅添加随机误差或者同时添加系统误差和随机误差,其对定位结果的影响都是系统性,对海底应答器定位结果的影响规律也是相同的,且均可由模型2予以削弱。

2.2 实测实验

本文使用的实测数据是来自日本在2020年6月采集的FUKU站的GNSS-A观测数据[34]。海底应答器及航迹如图5所示。

图5 实测测量船航迹及海底点分布Fig.5 Distribution of track and seafloor points of the measured ship

将模型2解算的传播时间作为时间参考值,主要目的是为了便于后续比较。模型1和模型2在不添加声速误差的情况下,二者的定位结果差值如表1所示。

表1 2种方法解算结果差值

由表1可知,2种方法的定位结果几乎一致,因此,将模型2确定的海底应答器坐标用于确定后续数值实验的参考值,供后续比较。

在上述数据的基础上,实验分为2个方案,具体同仿真实验。

2.2.1 方案1:仅对声速剖面添加系统误差

当仅对声速剖面的每一层均添加一固定声速扰动值时,其定位结果如图6所示。当海底应答器位于对称轴上(即海面航迹关于海底应答器成轴对称)时,与仿真数据不同的是,模型1中M11点的E方向定位误差比N方向小2个数量级,而M12点则相反,主要是由于海底应答器所处对称轴的不同,如图5所示。其中,较差的水平分量和垂直分量的定位误差优于仿真数据,这是因为在仿真数据中添加了GNSS天线误差所导致;从模型2的定位结果可得,当定位模型考虑声速剖面的时空变化时,其较差的水平分量和垂直分量可得到较大改善。当海底应答器位于海面航迹中心(即海面航迹关于海底应答器成中心对称)时,2个模型在水平方向的定位精度基本相当,优于厘米级,不同的是对垂直分量的改善程度。从图6可以看出,模型2有很好的改善效果。

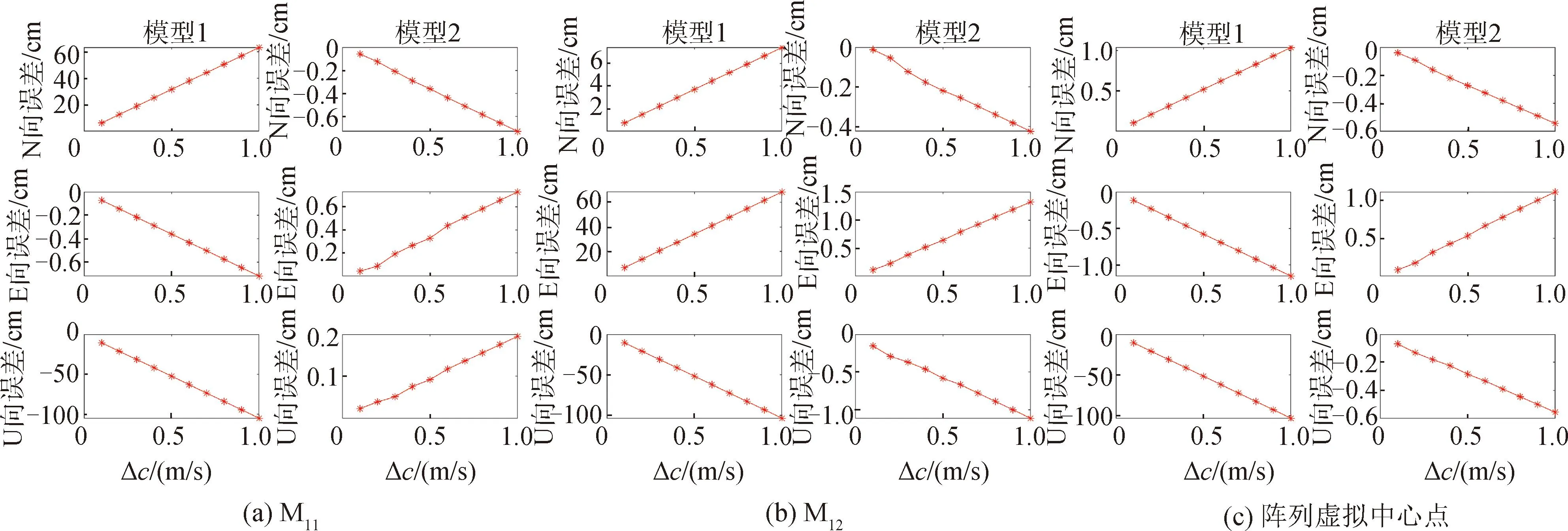
图6 海底应答器M11、M12以及阵列虚拟中心点与真值的误差Fig.6 Error between the seafloor transponder M11,M12 and the virtual center point of the array and the true value

2.2.2 方案2:仅对声速剖面添加随机误差

当仅对声速剖面的每一层添加服从正态分布的随机数(均值为零,每一层的标准差都相同)时,2个模型的定位结果如图7所示。当海面航迹关于海底应答器呈轴对称或中心对称时,其规律依然与仅对声速剖面添加系统误差一致,这是因为虽然声速剖面每一层存在随机误差,但在定位解算时,每个历元均使用的是同一个含相同声速误差的声速剖面,并不是每个历元使用各自历元所测量的声速剖面。因此,声速剖面随机误差对定位结果的影响呈系统性。并且,可由顾及声速剖面时空代表性误差的海底精密定位模型予以削弱。

图7 海底应答器M11、M12以及阵列虚拟中心点的STDFig.7 The STD of the seafloor transponder M11,M12 and the virtual center point of the array

以服从正态分布的随机误差(均值为0,标准差为0.5 m/s)和系统误差(每一层均添加0.5 m/s的声速扰动)为例,给出声速扰动对传播时间的影响,如图8所示。由图8可知,除数值不同外,随机误差对传播时间造成的影响趋势与系统误差基本一致,也可得出声速剖面随机误差对定位结果的影响与整体系统偏差规律一致。

图8 声速扰动对传播时间的影响Fig.8 The influence of sound speed perturbation on travel time

从距离残差来看,如图9所示。模型2的距离残差优于模型1的距离残差,且距离残差优于厘米级。因此,顾及声速剖面时空代表性误差的海底精密定位模型可将系统性的误差予以削弱。

图9 声速扰动导致的距离残差Fig.9 Distance residual caused by sound speed disturbance

3 结论

1)当海底应答器位于海面航迹的对称中心,即中心对称时,海底应答器水平方向的分量几乎不受声速剖面系统误差或者偶然误差的影响,声速误差主要反映在垂直方向。

2)当海底应答器位于海面航迹的对称轴,即轴对称时,对称轴所对应的水平方向上的分量误差比另一水平分量误差小1～2个数量级,声速误差主要反映在另一水平分量以及垂直方向。

3)无论是在声速剖面上仅添加系统误差、仅添加随机误差或者同时添加系统误差和随机误差,其对定位结果的影响都是系统性,对海底应答器定位结果的影响规律也是相同的,且均可由顾及声速剖面时空代表性误差的海底精密定位模型予以削弱。