海洋内波对海底精密定位的影响

王凯明, 薛树强, 韩保民, 肖圳, 周杰, 李保金

(1.中国测绘科学研究院, 北京 100830; 2.山东理工大学 建筑工程与空间信息学院, 山东 淄博 255049; 3.山东科技大学 测绘与空间信息学院, 山东 青岛 266510)

为实现高精度海底定位,通常采用GNSS-声呐组合观测系统(the global navigation satellite system-acoustic,GNSS-A),制约GNSS-A技术的首要因素为声速扰动引起的时空声速场系统误差[1],这种声速变化主要是由复杂的海洋温度、盐度和压力变化导致的[2],由此导致的海水密度垂向分层给海洋内波的产生提供了条件[3]。内波即产生于外力作用或者某一激发源持续波动的一种波,对水下潜器的安全性和稳定性能够产生很大的影响[4],同时内波的研究又对于海洋物理学、海洋动力学以及海底精密定位有重要意义[5],所以研究海洋环境中内波的时空变化特性变得极为重要。

由于声速场环境复杂,为了研究其特性和规律,通常可以使用波动理论、简正波理论、射线理论以及抛物方程理论等方法对声场进行建模研究,抛物线方程能够分层计算声场,有利于计算由内波导致的水平梯度变化对声场产生的影响[6],随着对内波的研究不断深入,国外学者的研究兴趣从二维层面扩展到四维时空层面[7],国内学者对于内波的研究主要集中于中国的南海海域[8],陈守虎[9]对这片区域的内波特点及内波的时空相关性进行了深入研究,刘进忠等[10]利用声学手段在声层析理论与技术研究的基础上进行反演内波特征,并计算声场的传播损失和声速剖面变化,这种方法后续可能使用在内波检测的研究技术中,秦继兴[11]研究了浅海中孤立子内波引起的声能量起伏规律,给出声场起伏的耦合简正波表达式并仿真。

由于我国处于临海国家,内波多存在于沿海城市附近,随着我国海洋声学的发展,在海洋环境资源利用方面和国家海洋发展战略的统筹下[12-13],内波的影响逐渐变得不可忽略,海水声速的时空变化会使声波沿传播方向发生折射,使得声波的实际传播路径为连续弯曲的曲线,有效消除声波的折射效应对提高GNSS-A水下定位精度至关重要,由于内波造成的这种误差会对海底应答器的定位产生影响,所以仿真海洋环境进行海底精密定位为水下导航定位和信号传输提供了一种有效便捷的方法[14],而不同海洋环境下的内波又对海底定位产生多大的影响或者是否符合一种规律变化,也是我们所关心的,因此建立一种附有内波仿真模型的时变声速场模型,研究其对精密海底定位的影响有重要意义。

1 GNSS-声呐组合定位模型与内波仿真模型

基于海面测量船装载GNSS-声呐组合系统对海底控制网进行观测可以实现海底扩展等较高时效监测、大尺度海底板块运动监测以及地震活动监测[15]。

海面测量船对海底应答器(PXP)进行主动式声呐观测如图1,D1、D2表示层间深度,ρ1、ρ2表示层间密度。声呐换能器于X1(n1,e1,u1)位置在T1时刻发出声信号,海底应答器X(n,e,u)在收到信号再返回换能器,此时位于X2(n2,e2,u2),接收时刻T2,即声信号往返传播时间为T=T2-T1,因此构建GNSS-声呐组合观测模型[17]:

图1 GNSS-声呐组合定位模型Fig.1 GNSS-Sonar combined localization model

T=Tstr[X1,X,C(n,e,u,t)]+

Tres[X2,X,C(n,e,u,t)]+δT+δdplr+εT

(1)

式中:Tstr、Tres为信号往返传播时间函数;δT为声信号硬件延迟;δdplr为多普勒误差;εT为随机误差;Tstr为信号的单程传播时间:

(2)

式中:L表示换能器与应答器之间的声线轨迹;c(L)表示声速剖面,传统的声线跟踪算法通过声速剖面分层计算深度方向的梯度然后计算声线的传播时间和位移等参量。

在实际中,时空四维声速场观测信息难以获取,往往只能获取声速剖面观测,因此时空声速场C(n,e,u,t)一般可以表示为只在深度方向的确定性声速C(u)和时空扰动声速δc(n,e,u,t)[18],即:

C(n,e,u,t)=C(u)+δc(n,e,u,t)

(3)

用于替代时空声速场进行水下定位,C(u)表示参考声速剖面,本文使用的是控制网的几何中心和开始时刻的声速剖面。因此,当使用参考声速剖面进行高精度定位时,必须考虑时空代表性误差影响,因此GNSS/声呐组合观测模型改写为:

T=Tstr[X1,X,C(u)]+Tres[X2,X,C(u)]+

δc+δT+δdplr+εT

(4)

式中δc表示使用参考声速剖面近似声速场引入的模型误差,在短时间尺度,海洋温度和盐度的整体变化可忽略不计,可假设声速时空扰动项δc(n,e,u,t)的变化主要由海洋中的内波导致的,而随着时空变化,密度垂向分层导致声速场在空间上存在显著的水平梯度,因此仅考虑声速内波扰动时,存在[20]:

δc(n,e,u,t)=Δ[z2-(z1+η(n,e,u,t))]

(5)

式中:z1、z2为上下两层的深度;Δ=(c1-c2)/(z1-z2)为声速垂向梯度;η(n,e,u,t)表示内波的时空位移解。在海洋中我们所能观测到的是一系列的周期性的振动波在移动,内波仿真模型是KDV方程的一种非线性的周期解,即Cnoidal波(椭圆余弦波)[22-23]:

η(n,e,u,t)=-Ht+(Ht+Hc)×

(6)

式中:Ht表示波谷;Hc表示波峰;k0表示波数;r(n,e)表示空间位置;s2表示参数,通常在0～1,决定非线性程度;cn2表示Jacobian椭圆余弦函数cn的平方,用于计算波面高度,这种椭圆余弦波常常表现为波面在波峰附近变得很陡,而两波峰之间间隔一段很长但又平坦的水面,即浅层区域下的有限振幅、长周期波,如图2(b)所示,Cnoidal波的具体形式需要以椭圆函数为理论基础进行展开,Jacobian椭圆函数在积分形式上表示为:

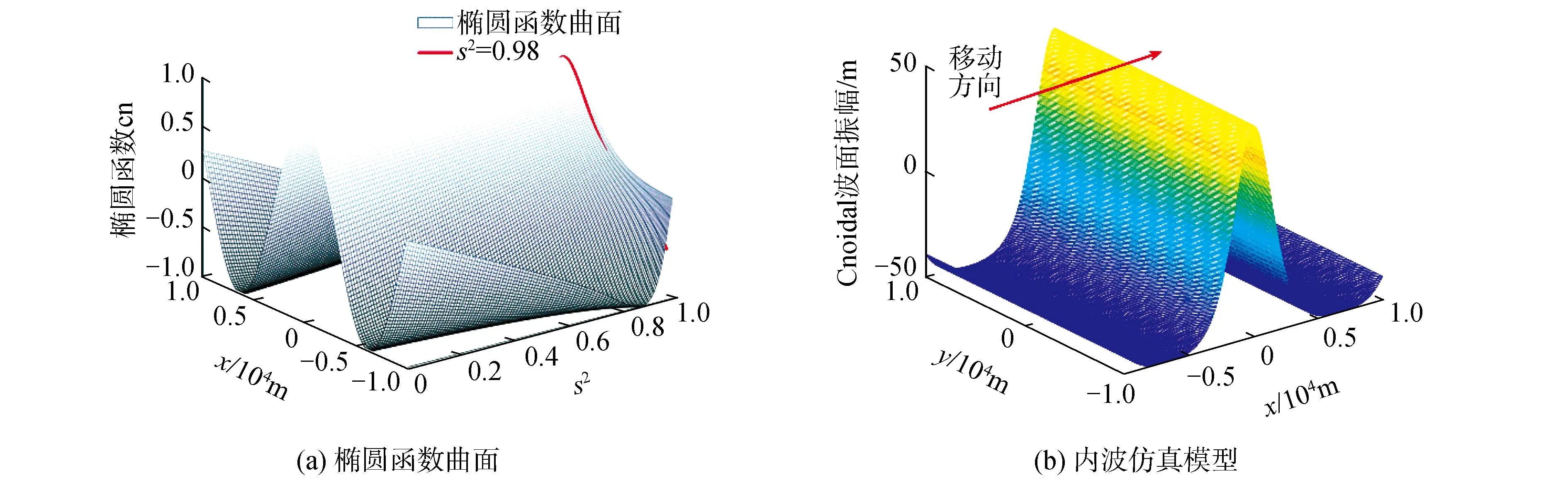
图2 椭圆函数曲面与内波仿真模型Fig.2 Elliptic function surface and internal wave simulation model

(7)

基本周期为:

(8)

cn(u)=cosφ

(9)

(10)

椭圆函数曲面如下图2(a)所示,自由参数s2通常取0.98,即图中曲线,确定椭圆余弦函数cn曲线建立三维Cnoidal波曲面,等价于三维空间上的所有质点组成的曲面运动,椭圆余弦波又为一种浅水波,波的形状在传播过程中保持不变,当波长趋于无穷时为孤立波。

2 海洋内波对海底定位精度的影响试验分析

2.1 时空声速场仿真与GNSS-声呐组合观测模型建立

本文参考声速剖面为零时刻声速剖面,在固定声速场中加入随时间变化的内波,声速剖面时序变化如图3所示,第1个波峰和波谷的时间点为0时刻和700 s时刻,浅海层声速扰动0～15 m/s,深层本文暂不考虑,时空声速场时间-深度-声速切片如图4,截取深度为浅海50 m处,不同时刻内波运动位置不同,声速值变化不同,海洋内波仿真达到有效性与真实性,为后续进行定位研究提供模型基础。

图3 零点处声速剖面时序变化Fig.3 Time series variation of sound velocity profile at zero point

图4 不同时刻时间-深度-声速切片Fig.4 Time depth sound velocity slices at different times

通过GNSS-声呐组合仿真观测,生成观测数据[19],海面观测图形与海底点布设如图5,当仅存在一个海底控制点时,或者为固定声速结构声速剖面定位时,采用图5(a)(海底点位于几何中心[0,0,-700 m])和图5(b)(海底点位于[±300 m,±300 m,-700 m])使用声线跟踪定位算法(模型1)[20-21],固定声速结构表示在固定时刻声速场固定,内波的方向与大小固定,对声速场的影响为此瞬时时刻受的内波影响,在航迹完成过程中内波保持静止。模型1表示在初始入射角和传播时间已知的前提下对声线的传播路径进行计算,而入射角计算是该算法的关键,该模型简单,计算精度较差,但是在数量级上可以明显观测内波的位置和方向信息。

图5 GNSS-声呐组合观测海面航迹与海底应答器位置Fig.5 GNSS-Sonar combined observation of sea surface trajectories and location of submarine responders

当存在多个海底控制点或者时空变化声速场动态定位采用图5(b),本文使用估计海洋声速梯度的水下定位模型(模型2)[25-26],时空动态声速场表示航迹完成过程中内波始终是随时间变化的,声速场也不断变化。模型2表示通过时空声速场的偏导数信息表征梯度信息建立声速场时空梯度影响补偿模型,主要是通过对时间或距离观测值施加时空梯度影响改正,以提高定位精度,这个模型可以进行海洋时空声速变化参数估计,通过这种方法可以有效提取海洋内波的影响,进行估计声速场的水平梯度参数并与仿真梯度进行对比,理论假设少,但是无法分离硬件延迟影响与声速时间代表性误差影响。

2.2 固定声速结构的静态声速剖面定位实验结果分析

海洋环境仿真设置一个N方向速度为1 m/s的内波,波峰波谷均为50 m,波数为1∶1 000,波数为波长的倒数。海底点位于几何中心,此时内波在固定时刻的位置导致声速场具有固定声速结构,航迹完成过程中声速场保持不变,从表1可知,对海底中心点进行定位时,定位误差与内波的方向和运动位置有关,位于波峰位置时,EN方向定位误差均小于10-3m,U方向定位误差-1.24 m,由波峰运动到波谷时,N方向定位误差先增大后减小,因此水平梯度变化也为先增大后减小再增大,U方向定位误差减小,E方向定位误差可忽略不计。

表1 固定时刻静态声速剖面中心点定位结果

由表2结果可知,对多海底点进行定位时,3个方向定位误差都会变化,且与内波运动位置具有直接关系,如图6所示,N方向误差由于水平梯度变化导致定位误差也变化显著,当位于波峰与波谷处时,EN方向定位误差都偏小,U方向误差偏大,波峰到波谷的过程时刻,水平梯度变化明显,定位结果也相应产生变化,中心点定位误差仍能反应内波方向。

表2 固定时刻静态声速剖面多海底点定位结果Table 2 Fixed time static sound velocity profile multiple seabed point positioning results m

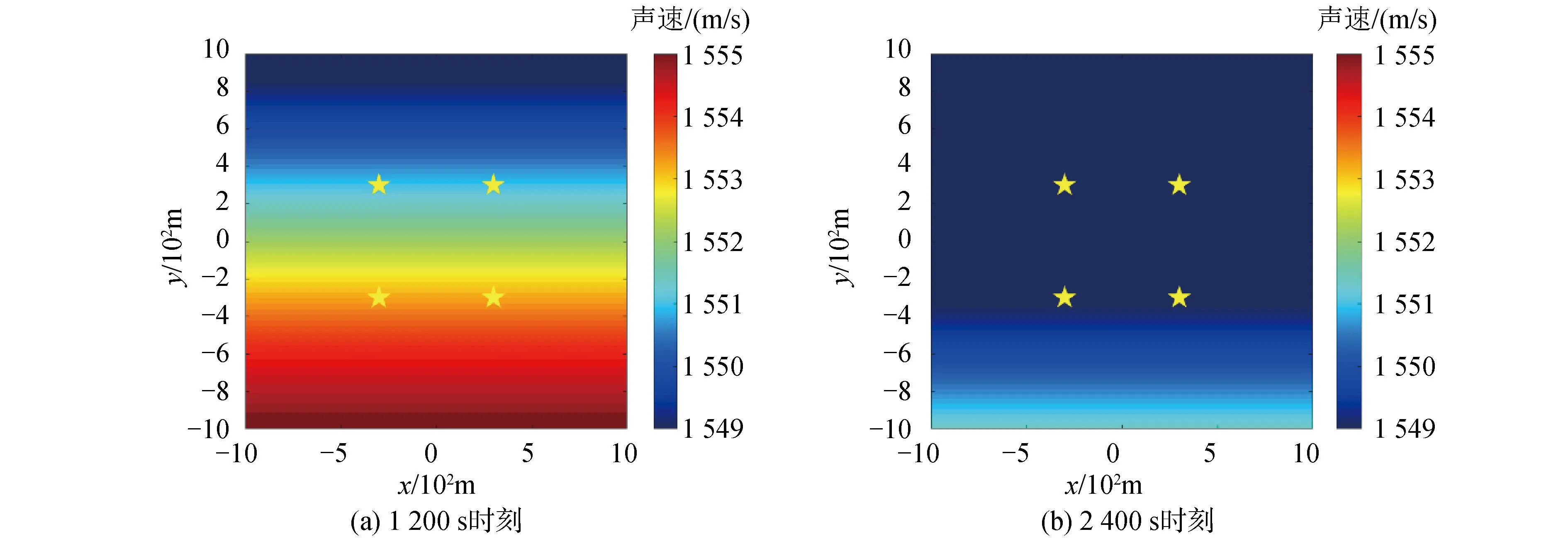
图6 海底应答器位置与内波运动位置Fig.6 Position of submarine responder and internal wave motion position

综上固定声速结构的静态声速剖面定位实验能够得到理想化的结论,海洋内波的方向与运动位置能够影响海底应答器的定位精度,且满足一定的规律变化,但考虑海洋是一个复杂的四维声速场,因此需要进行动态声速场仿真研究其复杂性与随机性,并进一步探讨海洋内波引起的时空声速场变化对定位的影响并进行水平梯度参数估计。

2.3 时空变化声速场动态定位结果比较分析

海洋环境设置为一个与2.2节相同的内波,但波数改为1∶10 000,海面图形与海底应答器布设如图5(b),通过仿真随时间变化的内波进行声速场动态定位,表3结果表明,模型1解算效果较差,EN方向定位误差在0.69 m左右,U方向误差在0.84 m左右,由此可见大尺度低频内波对定位的影响不可忽视,而模型2解算结果能够修正EN方向定位精度达到1 cm以内。

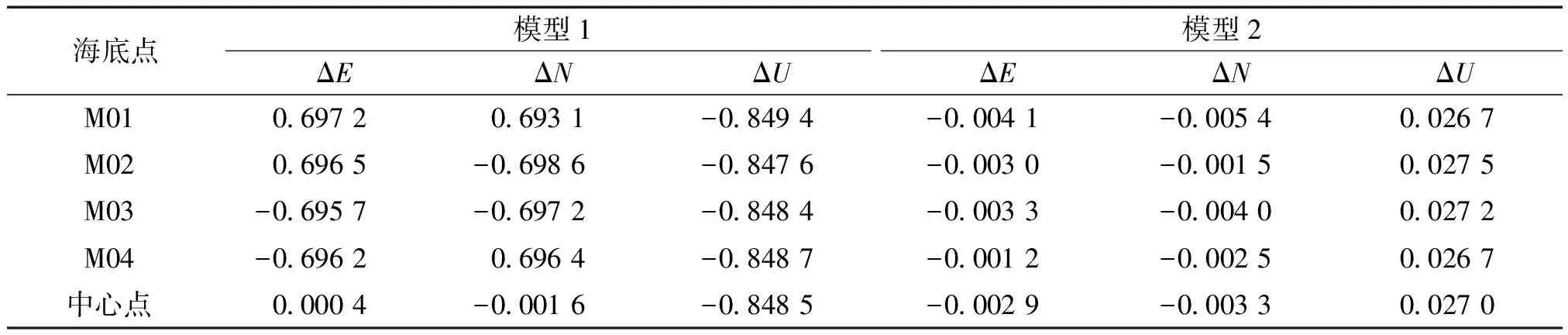
表3 2种模型解算对比结果Table 3 Comparison results of two model solutions m

本文只设置了一个移速非常慢的低频大振幅的内波,相当于海洋环境存在一个系统误差,而这个系统误差的来源于内波的频率与振幅导致,频率越快定位结果越差,振幅越大定位误差越大,海洋中还存在很多高频小振幅的内波,而在GNSS-声呐组合观测中有时难以监测到,具有随机性,所以为接近真实的海洋环境观测,增加一系列小尺度内波进行实验,参数配置如表4。

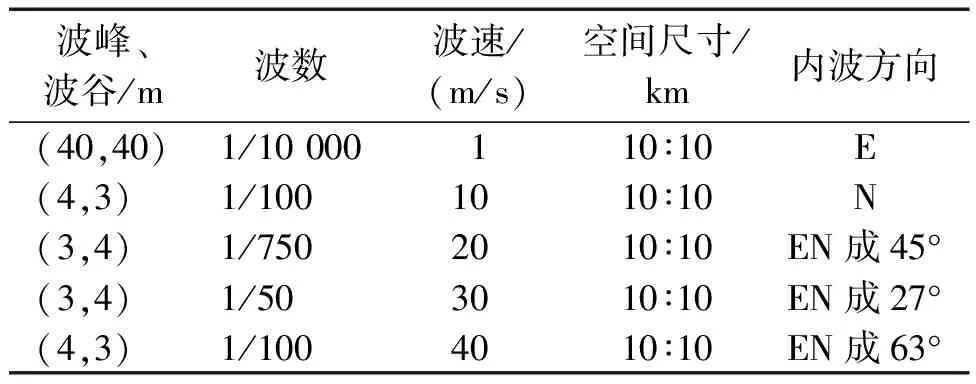
表4 参数配置3Table 4 Parameter configuration 3

如表5所示:模型1解算EN方向定位误差在0.64 m左右,U方向0.77 m左右,模型2的EN方向大部分都在1 cm以内,有的海底点定位误差在1～2 cm,U方向也是12～16 cm左右,由于多个内波的存在,可能某一时刻会多个内波交会的情况产生,所以U方向要相较于单个内波定位精度会变差,2种定位模型残差结果如图7所示,实验结果表明海洋环境具有随机性,小振幅高频内波会产生偶然误差对定位结果产生影响,但影响量级不大,主要定位误差来源还是大尺度低频内波导致。

表5 定位解算比较Table 5 Comparison of positioning solutions

图7 模型1和模型2的解算残差Fig.7 Model 1 residual and model 2 residual

2.4 时空声速场水平梯度估计实验与分析

内波仿真参数配置与实验方案设计如下:

方案1:海面航迹与海底控制点如图5(b)所示,仿真观测总时长4 h为一周期,设置一个10 000 m长尺度波包长方向为N的内波,内波移动速度为1 m/s。

方案2:海面航迹不变,仿真观测总时长4 h分为九个周期,海面船载观测一个周期大约26 min,内波设置与方案1相同。

方案3:海面航迹不变,仿真观测总时长与方案2相同,内波波长包改为1 000 m。

方案1结果(如图8)表明,在进行梯度估计的时候,船速与内波的移速都很慢,船与内波会形成相对运动趋势,并且4 h内船载只运动1个周期,内波运动会损失很多的信息,并且在进行梯度估计的时候正负梯度会进行平均化,估计不准确。

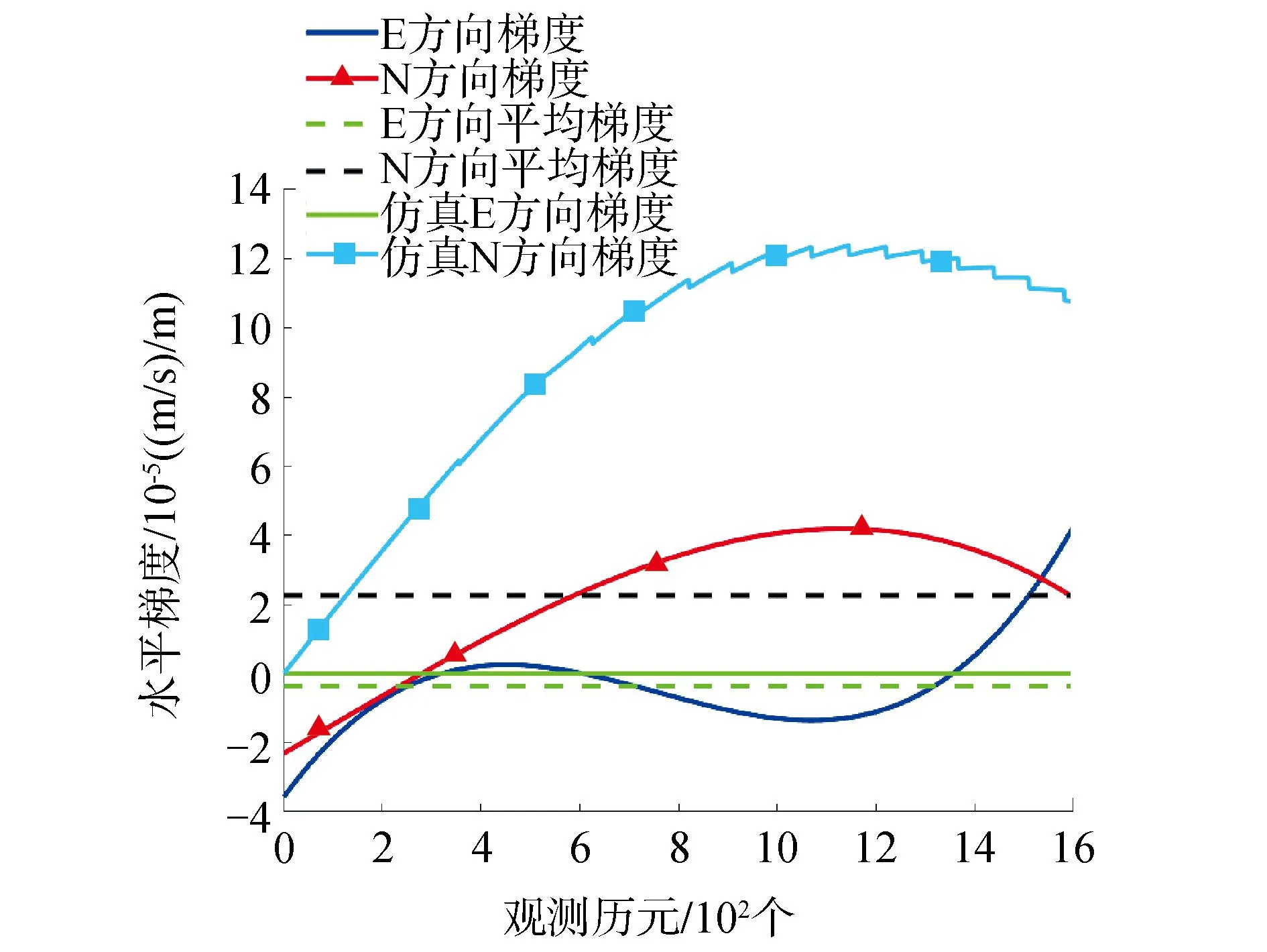
图8 方案1梯度分析结果Fig.8 Solution 1 gradient analysis results

方案2结果(如图9)表明,船速快,内波移速慢可看作相对静止,EN方向梯度估计差异明显,能够反映出内波的方向,但是与仿真的梯度还有一定的差距,因此海洋环境的水平梯度能否估计需要进一步通过方案3验证。

图9 方案2梯度分析结果Fig.9 Solution 2 gradient analysis results

方案3结果(如图10)表明,海洋环境的水平梯度可以进行估计,但是限制条件比较多,能够反演大致的内波的形状,但是在波峰位置反演并不准确,并且只适用于移动速度特别慢的内波运动,当波速快时,船速与波速的相对速度就产生不确定性,因此由于海洋环境的复杂性,声速场水平梯度很难刻画,而且与海面航迹尺寸,内波移速振幅等相关,而单海面船载测量与内波移动都会导致变量不唯一性,而真实海洋环境无法进行控制变量测量,因此刻画真实的海洋环境梯度需要进行多载体联合观测。

图10 方案3梯度分析结果Fig.10 Solution 3 gradient analysis results

3 结论

1)静态声速场环境下,不同时刻海底中心点定位结果与内波的移动方向有关,随着内波的移动,对海底定位误差的影响也反映出明显的变化规律,而定位误差的大小也与内波的振幅,移速,波长等因素相关,振幅越大定位误差越大,波速越快定位误差随机性越高。

2)航迹固定,海底点位置变化,EN方向定位误差会随之发生变化,影响量级与内波移动的位置有关,当位于波峰波谷时,定位误差较小,由波峰运动到波谷的过程中,误差变化具有一定规律性,声速扰动也存在正负梯度变化规律。

3)动态声速场仿真能够更加真实地反应海洋环境变化规律,由于海洋中大振幅低频内波的存在,这是导致定位误差的关键,即系统性的误差,而真实的海洋环境不止存在低频内波,还存在随机性的高频小振幅内波,这就导致在定位结果上出现随机性,对于低频内波而言,定位误差的大小与波速和振幅等有关,振幅越大定位误差越大,波速越慢定位精度越好,而高频小振幅内波的存在,也能够影响定位精度,但影响量级不大。

4)内波可引起超过1 dm的定位误差影响,考虑水平梯度参数估计,是确保厘米级精度水下定位的关键,当存在一个移速特别慢的内波时,通过改变船速可以将水平梯度大致反演出来,但是由波峰到波谷过程中,声速变化剧烈,反演并不完全准确,由于海洋环境复杂性,水平梯度大小与海面图形尺寸、船载航迹、内波方向、振幅、频率有关,单船载测量对实现水平梯度的刻画尤为困难,因此需要进行多载体联合观测才能实现有效反演。