联合匹配场和神经网络的声速时间场构建方法

李林洋, 徐天河, 王君婷, 黄威, 高凡, 舒建旭

(1.长安大学 地质工程与测绘学院, 陕西 西安 710054; 2.山东大学 空间科学与物理学院, 山东 威海 264209; 3.中国海洋大学 信息科学与工程学部, 山东 青岛 266100)

21世纪海洋经济的重心下移,近年来全球重大油气发现有70%来自水深超过1 000 m的水域,并且呈现逐年升高的趋势[1]。对于固定资源的深海采集工作高精度的水下导航、定位必不可少,而声速误差作为高精度水下导航、定位的主要误差源之一,构建高精度的声速场有着重要意义。水下声速剖面可以由声速剖面仪(sound velocity profiler, SVP)直接测量得到,或是通过温盐深剖面仪(temperature, conductivity, depth profiler, CTD)以及抛弃式温盐深剖面仪(expendable CTD, XCTD)经过声速经验公式获得。直接测量法获得声速剖面的优势是结果准确,但是采集效率低、成本高,无法进行大规模的声速剖面测量。

利用历史数据反演得到的声速剖面是海区历史或者平均声速剖面,不能据此准确地预测实际的声速剖面[2-3]。据此,周士弘等[4]有提出了至少利用5阶经验正交函数描述声速场,进而建立模型描述海区声速剖面,探讨了海面温度卫星遥感或航空遥感技术、海水温跃层水温预报技术同声速场经验正交函数描述方法结合在一起来预报海表以下深度的声速剖面。艾锐峰[5]利用后向传播(back propagation, BP)神经网络的自适应能力和自学习能力,以历史数据为样本对模型进行训练,得到反演预测模型进行声速剖面反演预测。禹小康[2]利用遥感数据提供的表面温度和神经网络进行声速剖面反演预测。但是使用神经网络模型构建需要大量的历史经验声速剖面作为参考样本,而对于局部海域经常面临参考样本稀少,容易导致模型过拟合而精度性能降低。

海洋声层析最初是由Munk和Wunsch提出的,在射线理论的基础上,通过匹配声场观测估计海洋环境参数[6-8]。Tolstoy[9]提出用匹配场方法(match field process,MFP)反演声速剖面。为了加快匹配场的反演过程,引入启发式算法,如粒子群算法(particle swarm optimization,PSO)[10-11]、模拟退火算法(simulated annealing, SA)[12]、遗传算法(genetic algorithm,GA)[3,13]。匹配场处理方法回避了建立声场信息到声速分布的反向映射关系的难题,为声速场构建提供了有效实现途径[14]。

针对上述方法所存在的问题,本文提出了联合匹配场处理和神经网络的声速时间场构建方法。母船走航或浮标采集的通信数据相较于直接测量声速剖面是便捷、经济的,而且其采集的通信数据较为完整且连续。首先该算法通过通信数据依照匹配场反演算法进行声速剖面仿真,加密参考样本。然后通过对非线性函数有较好拟合效果的BP神经网络进行EOF重构系数的拟合,形成时间(本文所使用的时间是距离2023年3月的秒计时)到EOF重构系数的非线性映射关系。最后根据BP神经网络构建出的模型输入XCTD时间生成声速剖面与实测XCTD结果进行对比。

1 MFPBP声速时间场构建

1.1 实验原理

1)EOF分解。

由于经验正交函数分解(orthogonal empirical function, EOF)能够显著降低反演参数数量,这对于匹配场处理有极其重要的作用,使用CTD与SVP的14条全水深声速剖面当作参考样本进行EOF分解,将分解得到的特征向量当作这片海区的基函数。通过反演EOF重构系数来生成声速剖面,经验正交函数求解过程如下。

将实测CTD与SVP的14条全水深声速剖面组合成矩阵的形式:

(1)

(2)

计算协方差矩阵R的特征向量VN×N和特征根λ(1,…,n),两者满足:

RN×N×VN×N=VN×N×ΛN×N

(3)

其中ΛN×N为:

(4)

对角线元素为特征根,将特征根从大到小排列,每一个特征根对应一个特征向量,也称EOF函数。取前k阶的正交函数,则任意声速剖面可以表示为:

(5)

式中:ai称为EOF重构系数;fi(z)为经验正交函数。将EOF投影到原始声速剖面数据上,即可利用最小二乘原理计算各声速剖面对应的EOF重构系数:

A=(VTV)-1V·ΔC

(6)

式中:A为EOF重构系数;ΔC为实际与均值的偏差矩阵。

2)匹配场处理。

由于经过EOF分解,任意声速剖面可以表示为:

匹配场算法实质是利用启发式算法拟合EOF重构系数,利用射线追踪原理模拟计算理论声场信息,通过理论声场信息与实测声场信息进行匹配用于指导启发式算法。

射线追踪理论在分层线性声速剖面近似模型下能够建立声速剖面分布到声场信息的映射关系,对于某一给定的声速剖面c(z),文献[15]给出了线性梯度声速层中信号传播时间、水平传播距离关于掠射角的计算公式:

(7)

(8)

式中:Δtj,i表示由信号源向第j个接收节点发送的信号在第i个深度层的传播时间;Δhj,i是相应水平传播距离;gi是第i个深度层的声速梯度;θj,i是由信号源向第j个接收节点发送的信号在第i个声速层的信号掠射角。当i=0时,θj,0是信号的初始掠射角,而c0是声速剖面的初始声速值。分层线性声速剖面近似模型中相邻声速剖面采样点之间声速变化是线性的,即:

ci=ci-1+giΔdi,i=1,2,…,I

式中Δdi是第i个声速采样点和第i+1个声速采样点之间的深度差。

上式信号传播时间和水平传播距离可以通过斯涅尔折射定律推导成与初始掠射角的关系。掠射角斯涅尔定律为:

c0cosθj,i=cicosθj,0,i=1,2,…,I

(9)

式中:ci为声速;θj,i为第j组收发节点的时延信息。在第i个深度层的掠射角,通过三角函数关系可得:

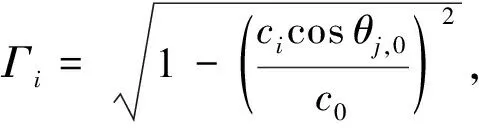
(10)

(11)

(12)

当使用启发式算法生成声速剖面时,可以通过对初始掠射角设定45°通过二分法由式(11)计算直达声所对应的h,再通过计算h和实际测量设置阈值来求得初始掠射角。通过初始掠射角求得时延t,通过式(12)计算损失函数来指导启发式算法,式中tcal为通信数据的测量值,即时延信息;tj为匹配场生成的时延;N为单个时段内通信数据的个数。

本文匹配场算法使用的启发式算法为遗传算法(genetic algorithm,GA)。遗传算法是借鉴生物的自然选择和遗传进化机制而开发出的一种全局优化自适应概率搜索算法[16]。能够提高匹配场收敛速度,提高计算效率。

其运算过程如下。

①初始化。采用二进制编码将EOF重构系数编码为基因型X,个体的表现型x和基因型X之间可以通过编码解码相互转化,设置进化代数计数器t←0;设置最大进化代数T;随机生成M个个体作为初始群体P(0)。

②个体评价。计算群体P(t)中各个个体的适应度,以式(12)作为适应度函数。

③选择运算。先计算出群体中所有个体的适应度综合∑fi;其次计算出每个个体的相对适应度大小fi/∑fi;最后产生0到1之间的随机数,通过随机数出现在哪一个概率区域来确定各个个体被选中的次数。

④交叉运算。先对群体进行随机配对;其次随机设置交叉点位置;最后相互交换配对染色体的部分基因。

⑤变异运算。首先确定各个个体的基因编译位置;然后依照某一概率将变异点原有基因值取反。群体P(t)经过选择、交叉、变异运算后得到下一代群体P(t+1)。

⑥终止条件判断。若t≤T,则:t←t+1,转到②;若t>T,则以进化过程中所得到的足有最大适应度的个体作为最优解输出,终止计算。

3)神经网络。

BP神经网络具有高度非线性映射能力,对于海洋复杂多变的环境引起的声速剖面的变化具有很强的适应性。图1为一个3层BP神经网络结构示意。

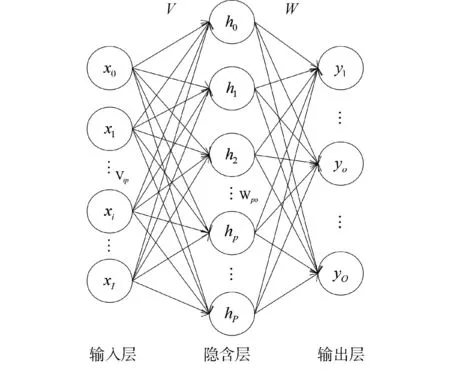
图1 神经网络示意Fig.1 Schematic of neural network

其中,输入层向量为X=[x1x2…xI]T,共计I个输入分量。隐藏层包括P个神经元。输出层向量为Y=[y1y2…yO]T,共计O个输出分量。输入层到隐藏层的权重向量为V=[vip],i=1,2,…,I,p=1,2,…,P,阀值为A=[a1a2…ap]T,其中ap=x0vop;激活函数为f1。隐藏层到输出层的权重向量为W=[wpo],p=1,2,…,P,o=1,2,…,O,阀值为B=[b1b2…bO]T,其中bo=h0w0o;激活函数为f2。于是:

(13)

(14)

1.2 MFPBP声速时间场构建确定步骤

本文给出了MFPBP声速时间场构建确定方法。算法流程见图2,详细流程如下。

图2 MFPBP声速时间场构建确定流程Fig.2 MFPBP sound velocity time field construction determination process

根据实测的数据进行声速剖面预处理,得到参考样本CTD与SVP的声速剖面14条和验证样本XCTD的声速剖面9条。

在通信数据预处理环节,通过母船换能器与海底应答器的距离除以大致声速1 500 m/s与实际测量的时延数据作对比,进行通信数据的选取。

对参考样本进行EOF分解得到参考样本的特征向量和EOF重构系数,取前5阶特征向量当作这片海区的基函数。

本文所使用的匹配场算法主要包含4个部分,通过EOF分解获得参考样本的特征向量;搜索主成分系数(EOF重构系数)并生成模拟声速剖面;根据射线追踪理论模拟计算理论声场信息;理论声场信息与实测声场信息匹配并将匹配时的模拟声速剖面确立为声速剖面反演结果。

匹配场反演出的EOF重构系数和参考样本的EOF重构系数作为神经网络的训练样本。以反演声速剖面所处时间(本文所使用的时间是距离2023年3月的秒计时)作为输入,EOF重构系数作为输出。隐含层节点数采用经验公式与试凑法确定:

式中:P为隐藏层节点个数;I为输入层节点个数;O为输出层节点个数a=[0,10]。

根据匹配场与参考样本的EOF重构系数的统计特性划定区间范围,以及相邻2个深度层之间声速差异是否满足阈值,进行神经网络训练。

将XCTD的测量时间换算距离2023年3月的秒计时输入到训练好的神经网络中反演出XCTD的声速剖面,与实际测量的XCTD声速剖面求解其RMSE值作为精度指标。

由于神经网络拟合具有随机性,这里使用拟合100次的EOF重构系数求平均来作为最终反演的声速剖面结果。

2 实验结果与分析

2.1 数据来源

本文所使用的数据是2023年南海海试数据,经处理后包括7条全水深(3 500 m)CTD数据、7条全水深(3 500 m)SVP数据和9条部分水深(2 200 m)XCTD数据,如图3所示。用于匹配场算法的数据有14条全水深(3 500 m)CTD与SVP数据、母船走航时的时延数据,以及在4个应答器上方和其中心静止时的时延数据。

图3 预处理后声速剖面数据Fig.3 Preprocessed sound velocity profile data

图4为实测声速剖面与其均值偏差剖面图,可以看到,其在1 500 m以后趋于稳定,并且相同仪器在深海与自身平均值的偏差趋向于0。图3末尾的分叉是由于SVP是直接测量,而CTD是通过经验公式间接测量,测量机理不同导致的系统偏差和数据预处理对深度不够的声速剖面进行线性延拓导致。

2.2 实验分析

声速剖面采用的是W.D.Wilson简化公式:

C=1 449.2+4.6T-0.055T2+0.000 29T3+

(1.34-0.01T)(S-35)+0.016D

经过声速剖面预处理插值为1 m为间隔的标准声速剖面层。对于某些声速剖面深度不够的采用线性延拓。

使用匹配场处理需要参考声速剖面样本的特征向量,以及应答器、换能器的位置和时延信息。图5为母船走航时的位置信息构成的轨迹图。采用每10 min为一组进行声速剖面反演,其代表时间为中间时刻。

图5 匹配场(MFP)使用的时延数据轨迹Fig.5 Time-delayed data traces used by matched field (MFP)

图6为通信数据预处理,由于通信数据的质量影响匹配场反演,需要对通信数据进行质量控制。采用母船换能器与海底应答器的坐标距离除以1 500 m/s简略计算时延,用计算的时延与真实测量的时延信息进行对比,观测其变化趋势。设定阈值从而进行数据的质量控制。

图6 时延数据预处理Fig.6 Preprocessing of time delayed data

本文使用平均声速剖面(AVG)、仅使用实测数据的BP神经网络和参考通信数据的MFPBP。3种算法进行对比。AVG计算公式为:

式中:CAVG,j为平均声速剖面(AVG)第j层的声速值;Cref,j为参考声速剖面第j层的声速值,本文指代CTD与SVP的14条声速剖面;n为参考声速剖面的个数。

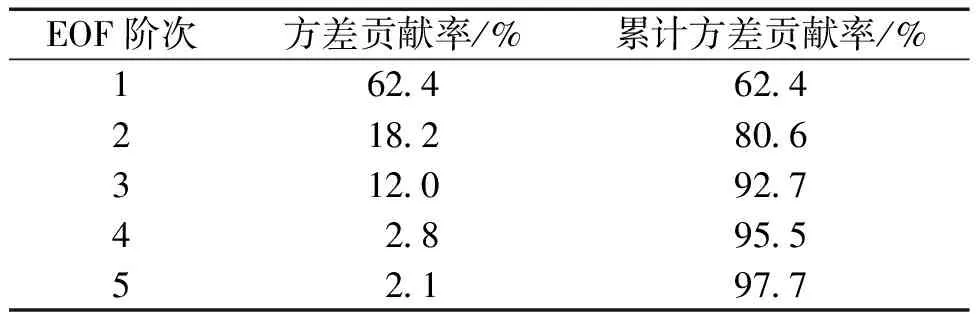
表1 EOF重构前5个阶次的方差贡献率

表2 结果精度RMSETable 2 Results accuracy RMSE

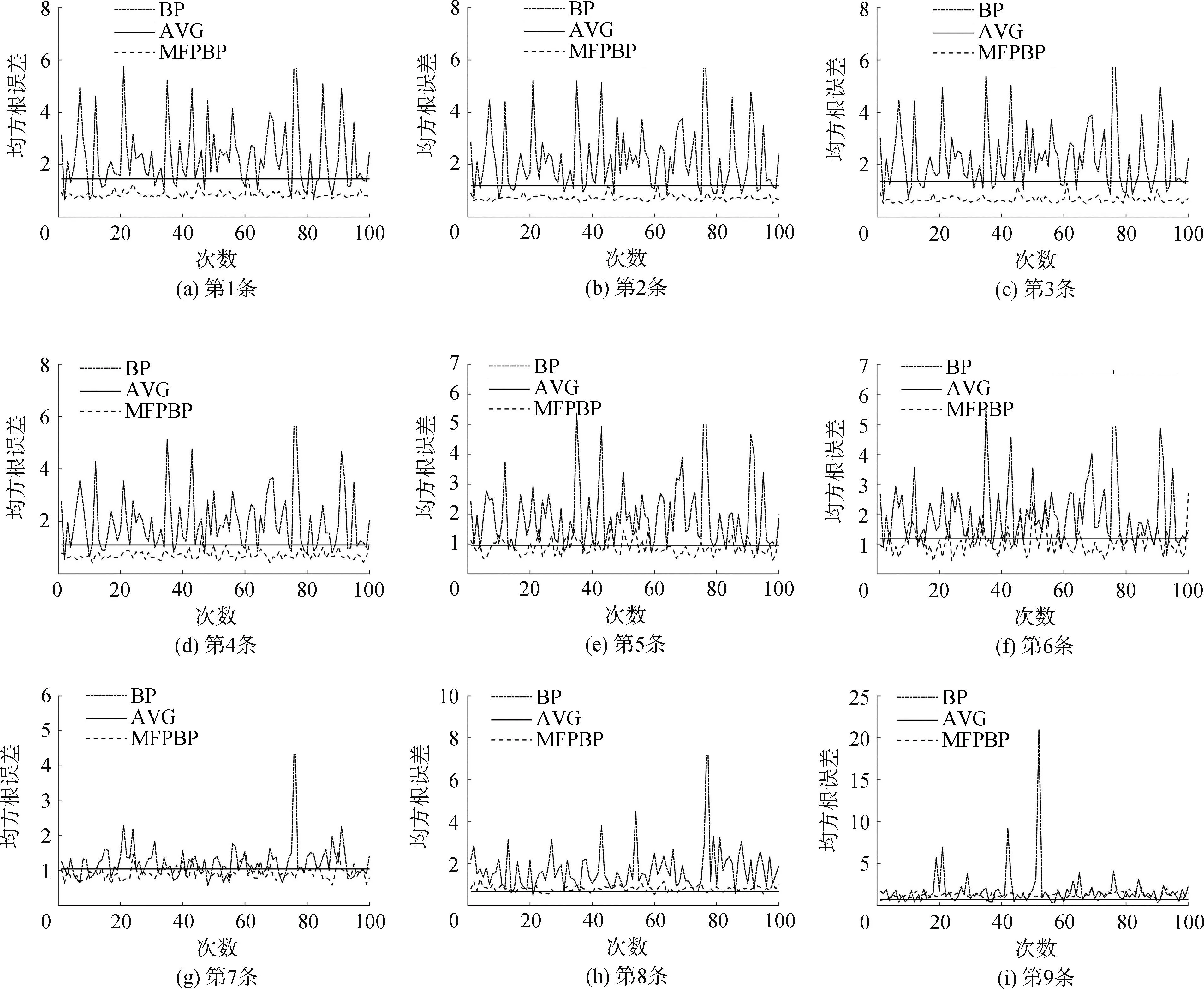
图7 AVG、BP、MFPBP反演声速剖面与XCTD实测声速剖面RMSEFig.7 AVG, BP, MFPBP inverted sound velocity profiles and XCTD measured sound velocity profile RMSE

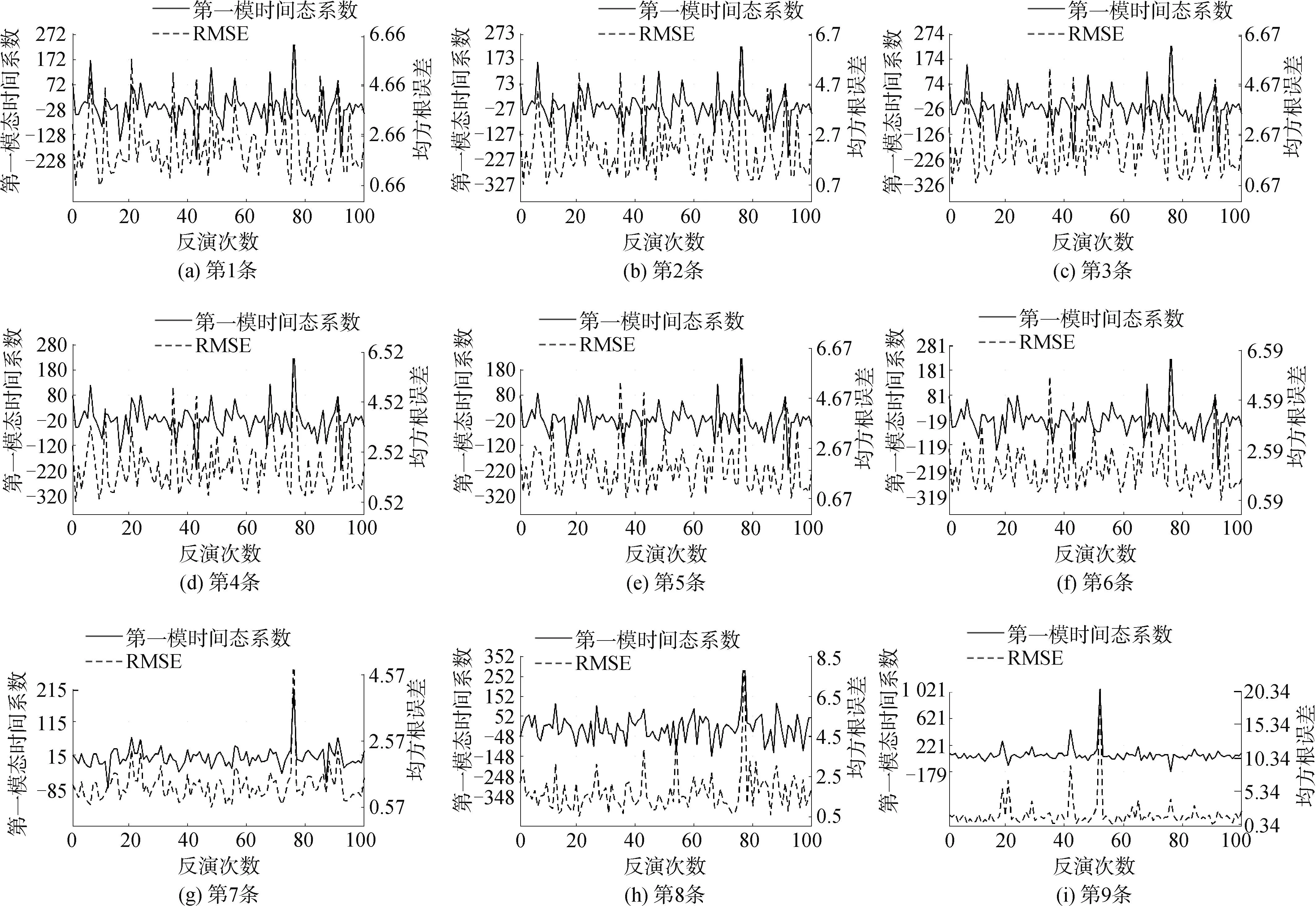
图8 BP反演EOF第一模态系数与XCTD实测声速剖面RMSEFig.8 BP inversion EOF first mode coefficient and XCTD measured sound velocity profile RMSE

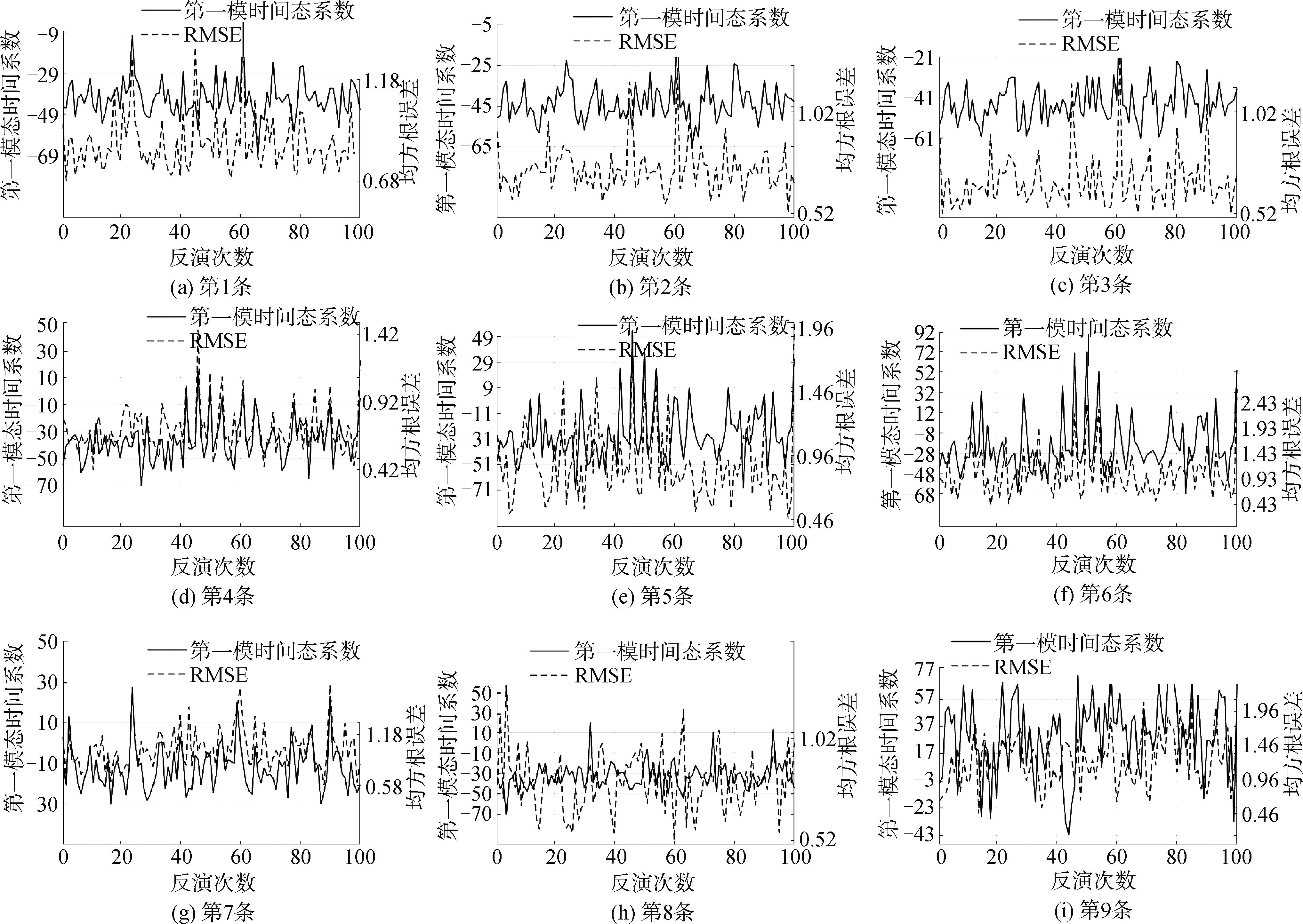
图9 MFPBP反演EOF第一模态系数与XCTD实测声速剖面RMSEFig.9 MFPBP inversion EOF first mode coefficient and XCTD measured sound velocity profile RMSE

从图10拟合声速剖面图可以得到,MFPBP反演的声速剖面与实测XCTD最为接近。BP反演的声速剖面在前5条验证数据在1 000～1 500 m处有较大突起。

图10 AVG、BP、MFPBP拟合声速剖面和XCTD实测声速剖面示意Fig.10 Schematic diagram of AVG, BP, MFPBP fitted sound velocity profiles and XCTD measured sound velocity profile

图11为通信数据与实测声速剖面数据的分布,其x轴为走航时的时间,是距离2023年3月的秒计时,y轴为由通信数据经过匹配场反演得到的声速剖面个数累加。从表2可以看出AVG的精度在7、8、9的精度较高,这是由于参考样本的区间范围在其附近,其平均值更能代表这附近的声速剖面。而使用了母船走航时的时延数据从图11可以看出其分布比较均匀和连续,其中出现时延数据间断可能是因为天气等其他原因避险所致。相较于AVG使用了匹配场反演的声速剖面MFPBP方法前6个验证数据精度提升幅度分别为0.693、0.569、0.789、0.560、0.348、0.477,这是由于前6个验证数据范围内没有实测参考数据,AVG算法精度不高,而MFPBP算法能够有效利用通信数据增加参考样本。第7个验证数据其精度相较于前6个提升有明显下降,提升幅度分别为0.187。而第8条验证数据和AVG精度相当。这可能是由于CTD的测量时段在其附近CTD平均值更能体现这片时间范围内的声速剖面。第9条验证数据从图9单次反演可以看出第一模态波动范围-20～50,波动幅度达到70,其精度RMSE也在0.5～1.9范围波动,可以看出单次反演其精度和第一模态波动相较于有匹配场反演数据的前8条验证数据波动巨大,稳定性差。从整体来看传统AVG的整体RMSE为1.079 m/s,而MFPBP反演的整体RMSE能够达到0.665 m/s,提高了38.4%。可以看出对于使用通信信息利用MFP反演的声速剖面对于参考样本过少时有着一定的可用性。

图11 通信数据与声速剖面数据的时间信息Fig.11 Time information for communication data and sound velocity profile data

3 结论

1)声速剖面反演结果表明,单纯用神经网络反演RMSE为1.315 m/s,如果添加匹配场反演的结果RMSE能够达到0.665 m/s,其精度提升了49.4%且稳定性更好。相较于传统AVG的RMSE为1.079 m/s,提高了38.4%。经过MFP进行加密后的BP神经网络拟合出的效果更好且更稳定。

2)通过对比前8条有匹配场反演数据的验证数据和第9条没有匹配场反演数据的验证数据从单次反演EOF第一模态的波动情况,可以看出匹配场对BP神经网络的稳定性有较大影响。

存在的问题:使用匹配场加密样本量时间复杂度过高,需要对其进行优化。使用MFPBP构建声速时间场精度的好坏还需从定位、导航方面进行分析。