考虑声线弯曲和深度约束的海洋大地基准网定位仿真分析

刘焱雄, 刘杨, 李梦昊, 陈冠旭

(1.自然资源部第一海洋研究所 海洋测绘研究中心, 山东 青岛 266061; 2.自然资源部 海洋测绘重点实验室, 山东 青岛 266061; 3.河海大学 地球科学与工程学院, 江苏 南京 211100)

为了贯彻我国海洋强国战略,需要构建综合多平台、多传感器的海洋大地基准网,以满足水面、水下和海底等多场景的声学导航定位应用需求[1-4]。

海洋大地基准网的导航定位性能与基准网网型结构、声信号传播特征、定位方法等密切相关[5-7]。目前基准网网型结构主要以海面浮标、水下潜标、海底基站等同型基站及其组合构型为主,基准网构型简单,且较多使用单频率声信号,无法满足大范围、多场景的导航定位需求[5-6,8-9]。孙文舟等[8]仿真了声信号传播距离与海底基站高度的关系,为了扩大基站的服务范围,需要提高基站高度。在声线弯曲、信号传播损失基础上,张旭等[6]利用直达声信号和海底一次反射声信号,仿真了正四边形基阵的定位效果,张志伟等[9]也进行了基于潜标基站的定位仿真,但基站类型、几何构型单一。为了优化基准网的几何构型,Li等[5]设计了综合声学浮标、潜标和海底基站的海洋大地基准网,采用单频声信号,仿真了不同几何构型的定位性能,并分析了声信号传播特征,但未充分考虑声信号传播路径弯曲对定位的影响。在算法方面,目前主要研究了考虑海洋声速误差的定位方法[7,10-11]。Xu等[12]提出了差分定位方法;Xue等[13]从理论上比较了非差和差分定位算法。为了进一步提高定位精度,赵建虎等[14]利用压力传感器提供的深度信息,提出了附加深度约束的声学定位方法;Chen等[15]综合研究了附加深度约束的差分定位性能;Sun等[16]考虑了附加深度和水平距离约束的差分定位算法。

本文在Li等[5]提出的综合基准网构型基础上,采用双频声信号,并考虑声信号传播路径弯曲,仿真分析附加深度约束的海洋大地基准网定位性能。

1 定位原理

根据目标与第i个声学基站间的声学传播时延观测Ti及目标搭载压力计提供的深度观测Dpress,可以建立声学时延观测方程为[14]:

Ti=t(x,xi)+δti+εi

(1)

Dpress=z

(2)

式中:t为由声线跟踪获取的声学传播时延[17];x、xi分别为目标位置向量、第i个声学基站的位置向量;δt为系统误差,包含声速误差、时延误差等[12];ε是随机误差。

利用多个声学基站的声学传播时延观测,并附加深度观测,分别构建式(1)、(2),并组成方程组(3),基于最小二乘,可以解算得到目标位置x。

y=Ax+ε,D(y)=D(ε)=P-1σ2

(3)

式中:y为声学时延和深度观测向量;A为设计矩阵;ε为观测值的随机误差向量;P为观测值的权矩阵;σ为单位权中误差;D代表方差。

本节讨论设计矩阵A中声学时延观测部分的解法。一种易于编程实现的数值解为[18]:

(4)

式中:(x0,y0,z0)为目标位置初值;Δ为微小的位置增量,如0.001 m。

也有研究给出了设计矩阵的解析解,如李昭[19]、Ramezani等[20]分别推导了基于常梯度声速剖面和等梯度声速剖面的解析解;Honsho等[21]利用角矩和水平距离给出了水平分量的解析解,垂向分量为数值解;Shan等[22]、Zhao等[23]则考虑了水平距离,且与Honsho等[21]在水平分量的解析解形式相似。

利用等效声速V可以将声学时延t表示为几何距离R。由于海洋声速随时间和空间变化,等效声速无法有效表征声速变化,需考虑等效声速误差项bv,有:

(5)

利用几何距离R,线性化的时延观测方程(1)可表示为[24]:

(6)

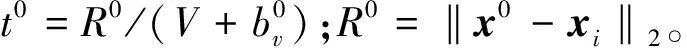
由式(5)对x、y、z、bv各项求偏导。

(7)

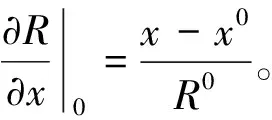
(8)

式中:Gx0为声速变化的水平梯度分量;Δ为x方向的位置增量,如0.001 m。

(9)

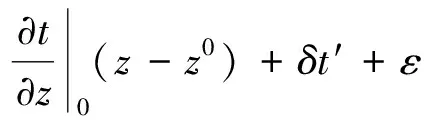
(10)

其中:

本文采用式(2)和式(10)组成观测方程组(3)。

2 海洋大地基准网定位仿真试验

不同基站发射的声信号均存在声线弯曲现象,影响基准网的信号覆盖范围和定位精度,因此本文主要仿真分析考虑声线弯曲的海洋大地基准网定位性能。采用的基准网构型如图1,包含4个海底基站,1个潜标基站及1个海面浮标基站,其中海底站阵形为正方形,浮标和潜标基站位于阵形中心。Li等[5]仿真结果也表明,利用该构型,通过调节海底基站间距、潜标离底深度可以有效扩大基准网的信号覆盖范围,并优化定位精度。为了进一步优化定位性能,本文假设基站搭载换能器均可发射2～4 kHz、8～16 kHz的双频声学信号,其性能及时延精度σT如表1。水下目标如潜航器,可以接收6个基站的声学信号,并搭载了压力计传感器,可以提供深度数据,其等效深度精度σD设置为1 m。参考声速剖面如图2,声道轴深度约1 000 m;等效声速误差σV约为0.2 m。为了简化仿真环境,本文假设基站与目标的时间同步,均具备高精度守时功能。本文不考虑基站的位置标校误差。通过长期的声学观测,目前海底大地基准点可实现分米至厘米级定位精度[25-26],海面浮标可由全球卫星导航系统(global navigation satellite system,GNSS)实现分米至厘米级定位精度[27-28],水下潜标位置受海洋动态环境影响,但保持短期稳定状态,可由水声定位获取[29-30]。

表1 声学信号参数Table 1 Parameters of sound signal

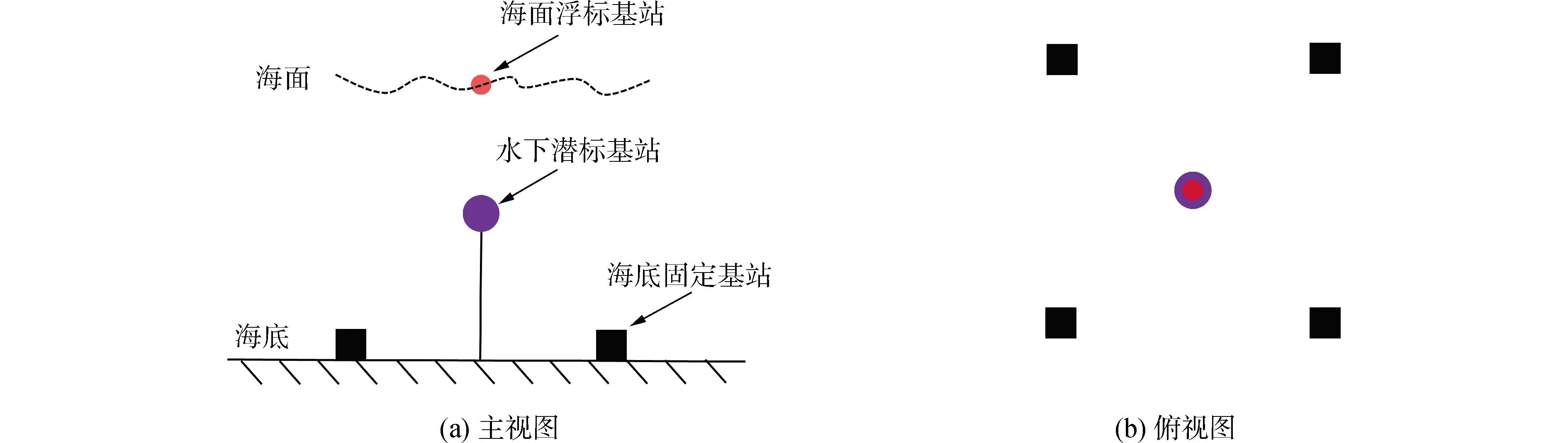
图1 基准网构型示意Fig.1 Schematic of the geodetic network

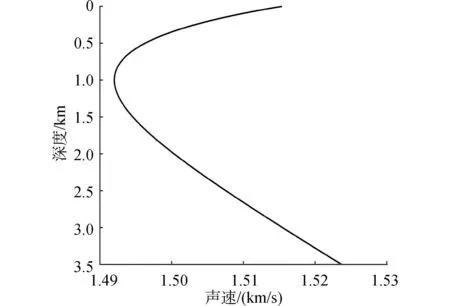
图2 声速剖面示意Fig.2 Schematic of the sound speed profile

本文仿真50 km×50 km×3 km的水下空间,并将空间格网化,水平方向格网间隔为5 km。假设水下目标深度为0.5、300和1 000 m,共仿真363个格网点处的定位结果。仿真的基准网几何构型变化包括相邻海底基站间距范围为1～25 km,潜标深度范围为0.5～3 km,海面浮标深度0.4 m。分析不同构型的定位性能,如基准网信号覆盖范围和定位精度。其中,信号覆盖范围考虑直达声信号可覆盖的格网点数目及每个格网点的有效测站个数;定位精度则比较定位结果与真实位置的偏差,如3个方向位置偏差分量、3D定位偏差等。

3 结果分析

本节分析了不同基准网构型的定位性能,如定位覆盖范围、有效测站个数和定位精度。图3给出了几类基准网构型的直达声信号覆盖范围及有效测站个数。

图3 有效测站个数分布Fig.3 Distribution of the available station number

由图3(a)可知,当相邻海底基站间距为5 km,潜标深度为0.5 km时,目标在0.5 m、300 m深度,基准网信号可基本覆盖50 km×50 km范围,但边缘区域无信号,存在盲区,随着目标深度增加至1 000 m,信号覆盖范围逐渐减少,边缘盲区增大。目标在0.5 m和300 m深度,距海底基站阵形中心20 km平面范围内,有效测站个数为4,随着距离增加,有效测站个数逐渐减少;目标在1 000 m深度,距海底基站阵形中心14 km平面范围内,有效测站个数以4为主,部分格网点的有效测站个数为5,随着距离增加,有效测站个数逐渐减少。

由图3(b)可知,当相邻海底基站间距为5 km,潜标深度增加至2.6 km时,基准网信号覆盖范围与图3(a)相似。目标在0.5 m和300 m深度,距海底基站阵形中心20 km平面范围内,有效测站个数主要为5,随着距离增加,有效测站个数逐渐减少;目标在1 000 m深度,距海底基站阵形中心14 km平面范围内,有效测站个数为4～6,随着距离增加,有效测站个数逐渐减少。

由图3(c)可知,当相邻海底基站间距为15 km,潜标深度为0.5 km时,目标在0.5 m深度,基准网信号可完全覆盖50 km×50 km范围,目标在300 m和1 000 m深度,边缘区域存在部分信号盲区。目标在0.5 m深度,距海底基站阵形中心15 km平面范围内,有效测站个数为4,随着距离增加,有效测站个数主要为1～3;目标在300 m深度,距海底基站阵形中心10 km平面范围内,有效测站个数为4,随着距离增加,有效测站个数为1～3;目标在1 000 m深度,距海底基站阵形中心7 km平面范围内,有效测站个数为4～5,随着距离增加,有效测站个数为1～4。

相比图3(c)、3(d)中潜标深度增加至2.6 km,基准网信号覆盖范围与图3(c)相似。目标在0.5 m深度,距海底基站阵形中心15 km平面范围内,有效测站个数主要为5,随着距离增加,有效测站个数为1～3;目标在300 m深度,距海底基站阵形中心10 km平面范围内,有效测站个数为5,随着距离增加,有效测站个数为1～4;目标在1 000 m深度,距海底基站阵形中心7 km平面范围内,有效测站个数为5～6,随着距离增加,有效测站个数为1～5。

通过比较图3(a)和图3(b),可以发现,海底基站和海面浮标位置相同时,潜标深度主要影响基准网的有效测站个数,增加潜标深度,海底基站阵形中心周围的有效测站个数随之增多;在图3(c)和图3(d)中可以发现相似的结果。通过比较图3(a)和图3(c),可以发现,潜标和海面浮标位置相同时,海底基站间距主要影响基准网信号的覆盖范围,增加基站间距可以扩大基站信号覆盖范围。当相邻基站间距为15 km时,能够实现0.5 m浅水深度、50 km×50 km范围内的信号全覆盖,当目标深度增加时,边缘区域无可用信号。另一方面,远离海底基站阵形中心的有效测站个数随着海底基站间距增加而减少。

图4给出了不同基准网构型对应的3D定位偏差累积分布函数(cumulative distribution function,CDF),其基准网构型、目标深度与图3相同。当格网点的可用测站个数不少于2,本文称之为有效定位格网点。在有效定位格网点总数基础上,本文统计了对应范围内的3D定位偏差CDF,由图中曲线表示,并将3D定位偏差为30 m时的位置标记为虚线。

图4 3D位置偏差统计Fig.4 Statistic of 3D position deviation

由图4(a)可知,当相邻海底基站间距为5 km,潜标深度为0.5 km时,在20 km×20 km平面范围内,格网点总数为25,目标在0.5 m、300 m和1 000 m深度,有效定位格网点总数均为25。相对于不同目标深度的有效定位格网点总数,可以发现,约96%的格网点3D定位偏差小于7.0 m、小于11.7 m和小于25.1 m。在20 km×20 km平面范围外,格网点总数为96,随着目标深度的增加,基准网信号覆盖范围(图3(a)),不同目标深度的有效定位格网点总数也逐渐减少,分别为72(75%)、48(50%)和32(33.3%)。3D定位偏差统计结果为小于41.0 m(68%)、小于34.8 m(68.8%)和小于48.5 m(56.3%)。当基站间距不变,将潜标深度增加至2.6 km时,如图4(b),有效定位格网点总数不变。在20 km×20 km平面范围内,约96%的格网点3D定位偏差小于9.1 m、小于20.1 m和小于37.3 m;在20 km×20 km平面范围外,3D定位偏差表现为小于41.4 m(68%)、小于46.65 m(68.8%)和小于49.5 m(56.3%)。

由图4(c)可知,当相邻海底基站间距为15 km,潜标深度为0.5 km时,在20 km×20 km平面范围内,不同目标深度的有效定位格网点总数均为25(100%)。约96%的格网点3D定位偏差小于18.2 m、小于21.9 m和小于34.1 m。在20 km×20 km平面范围外,不同目标深度的有效定位格网点总数分别为72(75%)、52(54.2%)和36(37.5%)。3D定位偏差统计结果为小于24.2 m(68.1%)、小于16.3 m(69.2%)和小于40.0 m(69.4%)。由图4(d)可知,当基站间距不变,将潜标深度增加至2.6 km时,有效定位格网点总数不变。在20 km×20 km平面范围内,约96%的格网点3D定位偏差小于10.9 m、小于14.8 m和小于27.3 m;在20 km×20 km平面范围外,3D定位偏差表现为小于22.9 m(68.1%)、小于24.4 m(69.2%)和小于54.5 m(69.4%)。

通过比较图4(a)和图4(b),可以发现,海底基站和海面浮标位置相同时,随着潜标深度的增加,不同目标深度的3D定位偏差增加,可能的原因是相邻海底基站距离较近(5 km),且潜标更加靠近海底基站,目标与基准网之间构成了差的几何结构,导致定位偏差未随测站数增加而减少。进一步比较图4(c)和图4(d),将相邻海底基站间距扩大至15 km,目标与基准网之间构成的几何结构得到了改善,随着潜标深度的增加,在20 km×20 km平面范围内,不同目标深度的3D定位偏差均降低,在20 km×20 km平面范围外,0.5 m深度的3D定位偏差降低,300 m和1 000 m深度的3D定位偏差增加。

对于不同构型的基准网,在0.5 m和300 m深度、20 km×20 km平面范围内,附加深度约束的3D定位偏差均小于30 m。受声信号传播、定位精度、基准网构型等因素综合影响,在20 km×20 km平面范围外,不同深度的3D定位偏差均大于30 m。

4 结论

1)潜标深度和海底基站间距均影响基准网的有效测站个数。增加潜标深度,海底基站阵形中心周围的有效测站个数随之增多;增加海底基站间距,远离海底基站阵形中心的有效测站个数随之减少;

2)海底基站间距也影响基准网信号的覆盖范围,增加海底基站间距可以扩大基准网的信号覆盖范围。相邻基站间距为15 km时,能够实现在浅水、50 km×50 km平面范围内的信号全覆盖,在深水的边缘区域则存在信号盲区;

3)潜标深度和海底基站间距综合影响基准网定位精度,适当扩大海底基站距离,基准网定位偏差可随着潜标深度的增加而减小;

4)在0.5 m和300 m深度、20 km×20 km平面范围内,附加深度约束的基准网3D定位偏差小于30 m。受声信号传播、定位精度、基准网构型等因素综合影响,在20 km×20 km平面范围外,3D定位偏差均大于30 m。

本文仿真分析了考虑声线弯曲和附加深度约束的海洋大地基准网定位性能,可为优化海洋大地基准网及其建设应用提供参考,而海洋环境及复杂海洋声速时空变化等对定位的影响仍需进一步研究。