考虑双程声径的走航式水下差分定位方法

王兆喆, 王振杰, 秦学彬, 赵爽

(1.中国石油大学(华东) 海洋与空间信息学院, 山东 青岛 266580; 2.中国石油集团东方地球物理勘探有限责任公司 海洋物探处, 天津 300457; 3.中国测绘科学研究院 大地测量与地球动力学研究所, 北京 100036)

随着我国海洋强国战略的快速推进,海底大地基准的建设广泛开展,需要通过全球导航卫星系统/声学(global navigation satellite system/acoustic,GNSS/A)定位技术[1-2]获取高精度的海底大地基准点三维绝对坐标。由于受到水声仪器硬件延迟以及声速结构时空变化等因素的影响,水下声学观测值中不可避免地包含了系统误差;同时由于走航测量载体持续移动观测的特点,基于单程声径的传统水下定位模型会受到收发时刻位置差的影响,一定程度上降低了定位精度。

海洋环境具有复杂性和多变性,在水下声学定位中,水下目标的定位精度受多种误差源的影响,其中声速相关误差等是制约水下定位精度最显著的因素之一。在声速相关误差处理方面,国内外学者从不同角度开展了大量的研究,尤其在水声定位模型构建方面提出了一些卓有成效的方法。针对传统非差定位函数模型无法消除观测值中系统误差的问题,可以借鉴陆地卫星定位中历元间差分和空间差分的思想,消除或削弱观测值中包含的共性误差。Xu等[3]将差分方法应用于水下声学定位,通过历元间差分消除应答器时延误差的影响,并削弱声速相关误差的影响。赵爽等[4]提出将基于选权迭代的抗差估计与水下差分方法相结合,同时削弱水下声学观测值中存在的粗差和声速相关误差的影响。孙文舟等[5]针对水下差分定位方法垂直方向定位精度低的问题,在水下差分方法的基础上附加水下控制点间水平距离和深度差约束,有效改善了水下目标定位的垂直解精度。

除了差分方法外,Zhao等[6]考虑海面换能器的位置误差,首次提出了考虑海面位置误差的水下联合平差方法,有效减弱了海面换能器位置误差对水下定位的影响。Yang等[7]通过引入分段二阶多项式对残差序列中包含的系统误差进行拟合,提出了考虑周期性系统误差参数的水下弹性定位模型,能够有效补偿声学测距系统误差。对于时变、空变声速误差的处理,国内外学者提出采用拟合、声速剖面修正等方法,削弱声速时空变化对水下定位精度的影响[8-11]。

除了声速相关误差外,海面测量载体收发时刻位置差也是制约水下声学定位精度的重要因素之一[12]。传统水下声学定位方法仅考虑测距声信号的单向传播,忽略了海面测量载体在测距声信号往返过程中发生的位移,进而影响了水下定位精度。针对该问题,一些学者提出改进的考虑双程声径的水下定位模型,并结合声线跟踪、深度约束等方法进一步提高了水下定位的精度[13-14]。

鉴于目前海底大地基准建设等领域大多采用海面测量载体走航式观测的定位方法[15],本文针对走航式水下声学定位中存在的海面测量载体收发时刻位置差以及硬件时延、声速相关系统误差等,提出了考虑双程声径的水下差分定位方法,对考虑双程声径的水下差分定位函数模型和随机模型进行了推导,并通过仿真和实测算例对该算法的有效性进行了验证。

1 传统水下定位模型

在水下定位中,非差定位模型不能很好地消除来自水面、水下的各类系统误差[16],因此国内外专家学者借鉴在陆地卫星定位中已广泛应用的差分定位思想,将水下声学观测值历元间做差,有效削弱或消除硬件时延、声速代表性系统误差等。

1.1 水下差分定位模型

为了削弱GNSS/A观测中硬件时延、声速代表性系统误差等对海底基准点定位的影响,进一步提高水下定位的精度,可参照卫星无线电波定位的差分算法构建水下声学差分定位模型,本文以走航式单差定位为例进行说明。

以ti时刻为例,换能器坐标为xi,由声学观测所得时延乘以平均声速可以得到换能器至应答器之间的斜距ρi。对于连续的观测时刻ti、tj,则有:

ρi=f(xo,xi)+δρdi+δρvi+εi

(1)

ρj=f(xo,xj)+δρdj+δρvj+εj

(2)

式中:f(xo,xi)、f(xo,xj)分别为ti、tj时刻换能器到应答器的真实距离;δρdi、δρdj为ti、tj时刻对应的应答器时间延迟造成的系统误差;δρvi、δρvj为ti、tj时刻对应的由声速结构造成的系统误差,这主要来源于忽视了声速时空变化特性,认为声信号传播过程中声速结构没有发生变化的假设;εi、εj为ti、tj时刻的测距随机误差。将式(1)与式(2)线性化后可以得到:

(3)

(4)

式中:ai、aj为ti、tj时刻f(xo,xi)、f(xo,xj)对应答器位置参数一阶导数的系数;bi、bj为ti、tj时刻f(xo,xi)、f(xo,xj)对换能器位置参数一阶导数的系数。将式(3)和式(4)作差分运算后得到:

Δρij=(aj-ai)xdo+Δρdij+Δρvij+Δεij

(5)

差分运算基本消除因应答器时间延迟和声速结构造成的系统误差,则观测方程可统一表示为:

l=Axdo+εl

(6)

式中:l为观测向量;A为观测方程系数矩阵;εl为随机误差向量。

使用最小二乘原理解算海底应答器坐标改正值:

xdo=(ATPA)-1ATPl

(7)

通过式(7)所得结果对应答器坐标初值进行改正,将得到的坐标作为初值重新迭代解算,直至相邻2次改正数之差小于阈值即可得到所求应答器三维坐标。

1.2 基于单程声径的水下定位模型存在的缺点

在传统基于单程声径的水下定位模型中,由于无法直接获取测距声信号从播发位置至海底应答器的时间延迟,所以对于测距声信号传播时延的处理策略为:将海面测量载体观测得到的测距声信号往返时间的一半作为声信号单程传播时间[17],即:

teq=tobs/2

(8)

式中:tobs为实际观测中得到的声信号总时间延迟,包含下行和上行信号时延、应答器时延误差以及声速结构变化造成的误差,即tobs=tdown+tup,teq即为换算得到的等效单程传播时间。

在实际走航式定位作业中,海面测量载体按预定航迹匀速航行,一般采用圆航迹、多折线航迹或组合航迹开展GNSS/A观测[18]。如图1所示,当采用圆航迹进行GNSS/A观测时,由于航迹上各个位置到海底应答器的斜距都是近似相等的,所以测距声信号下行和上行的时间延迟也是近似相等的(图1(a)),那么采用上述的将测距声信号往返时间的一半作为声信号单程传播时间的处理策略是合适的;当采用多折线航迹或组合航迹进行GNSS/A观测时,则在绝大多数情况下,海面测量载体在测距声信号发射位置、接收位置到海底应答器的斜距不相等,那么测距声信号下行和上行的时间延迟也不能认为是近似相等的(图1(b)),若继续采用上述的处理策略,显然会引入由于海面测量载体收发时刻位置差引起的系统性误差,降低海底大地基准点的定位精度。

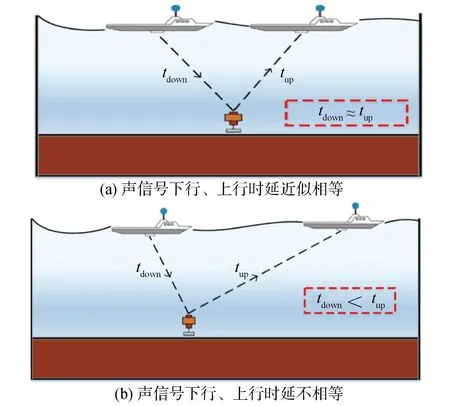
图1 船载换能器收发时刻位置差示意Fig.1 The diagram of coordinate′s deviation error of on-board transducer

2 考虑双程声径的水下差分定位模型

为了进一步削弱系统误差对水下定位精度的影响,结合1.1节中所述的水下差分定位思想,提出了考虑双程声径的水下差分定位模型,通过构建双程声径模型和差分运算削弱或消除海面测量载体收发时刻位置差以及硬件时延、声速代表性系统误差等的影响。

2.1 函数模型

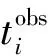
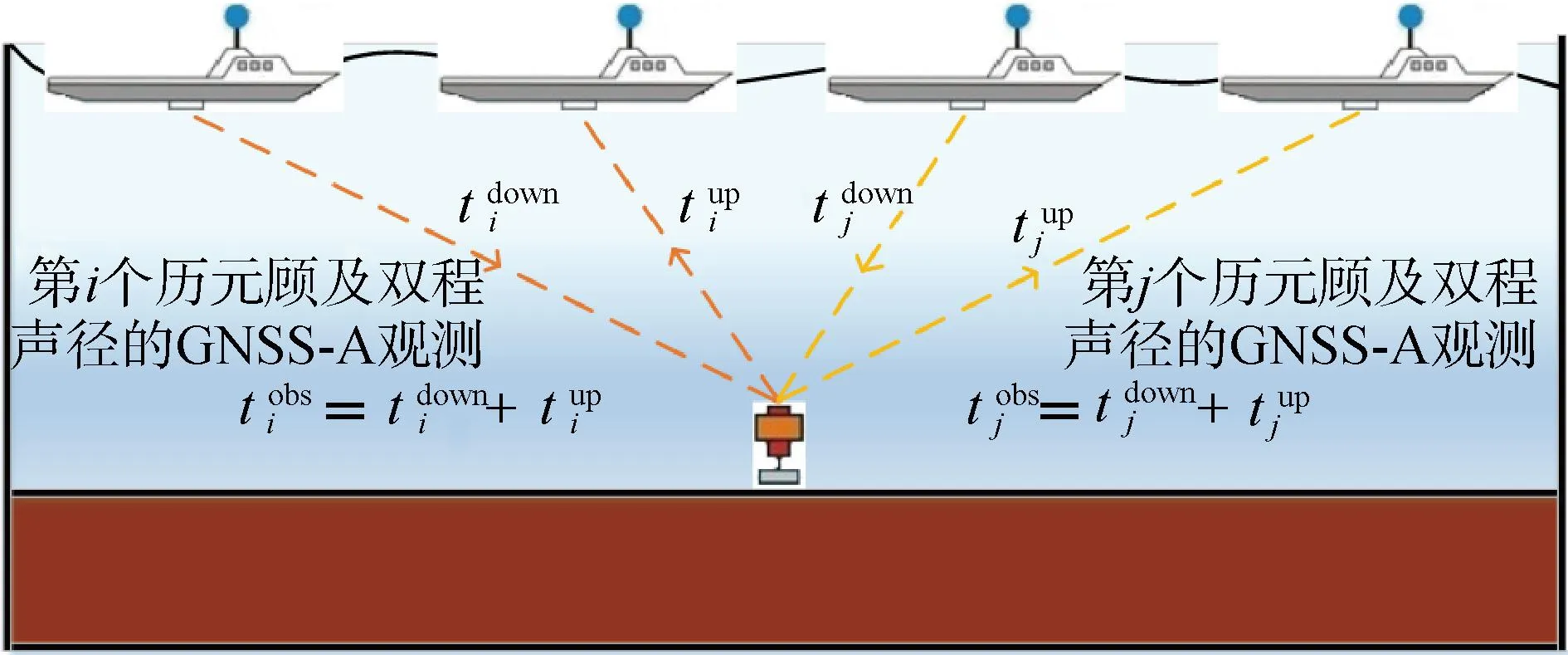
图2 顾及双程声径的水下差分定位示意Fig.2 The diagram of underwater difference positioning considering round-trip acoustic path

根据考虑双程声径的水下定位原理,则有:

(9)

(10)

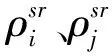
将式(9)和式(10)线性化后可以得到:

(11)

(12)

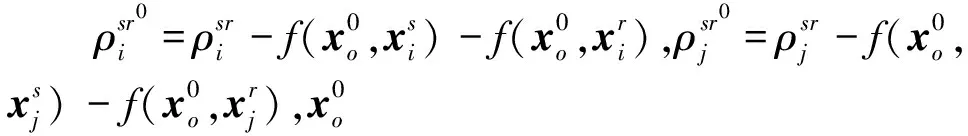
差分历元选择标准包括相邻历元差分、间隔历元差分等,其本质为选择不同的观测历元对相应观测值进行差分运算。本文基于相邻历元测距声信号经过的声速结构近似相同的假设,将式(11)和式(12)作相邻历元差分运算后得到:

(13)

式中:

与基于单程声径水下定位模型对相关系统误差的推论类似,当海面测量载体进行2次连续的考虑双程声径的GNSS/A观测时,由于2次观测针对的是同一个应答器,则差分运算可以消除应答器时间延迟造成的系统误差,即Δρdij=0;若认为2次连续的考虑双程声径的GNSS/A观测在空间和时间上足够接近,那么2次观测的声信号传播经过的声速结构就是相似的,则可以认为声速结构造成的系统误差在差分运算后基本被消除,即Δρvij≈0。则观测方程可以统一表达为:

l=Axdo+Δεl

(14)

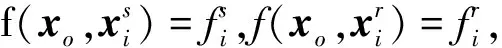
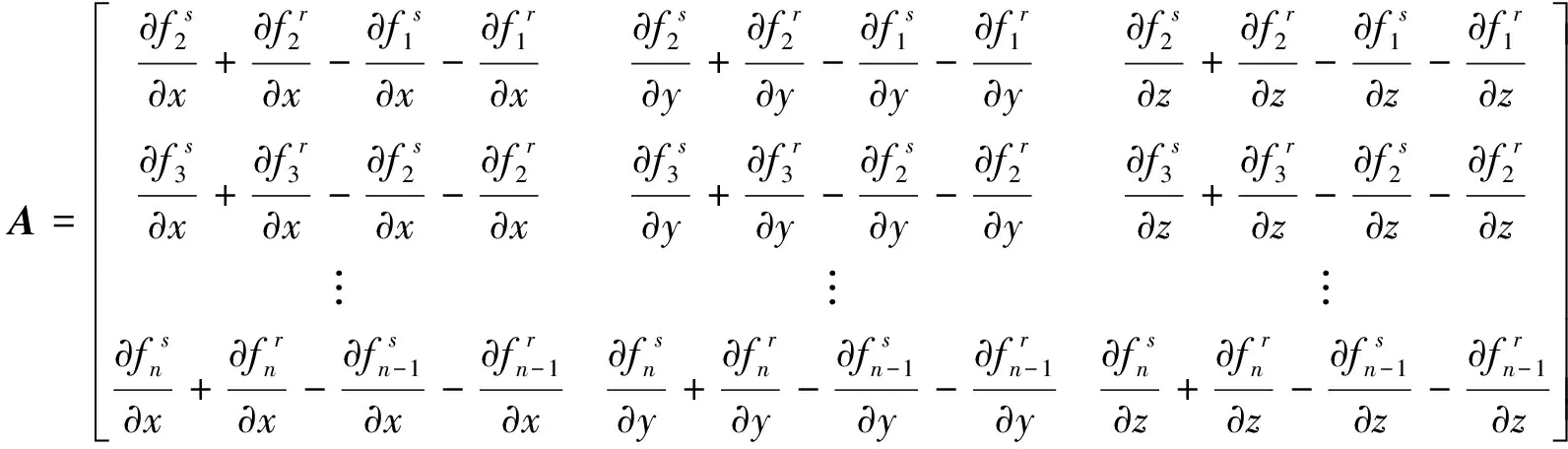
使用最小二乘原理解算海底应答器坐标改正值:

xdo=(ATPA)-1ATPl

(15)

与1.1节中所述相同,需要通过迭代解算得到海底应答器的三维坐标。

观测值改正数为:

V=Axdo-l

(16)

2.2 随机模型

基于最小二乘原理可知,考虑双程声径的水下差分定位模型法方程为:

ATPAxdo-ATPl=0

(17)

式中矩阵P为考虑双程声径的水下定位观测值对应的权矩阵,下面对权矩阵P进行推导。

式(14)中的偶然误差项可表示为:

(18)

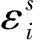
换能器位置误差主要包括动态GNSS定位误差和姿态误差,由于姿态误差相对较小,则可以用动态GNSS的定位误差来代替换能器位置误差。

观测值误差协方差阵为:

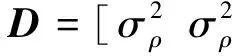
(19)

由式(18)根据协方差传播率:

DD=CDCT

(20)

而

(21)

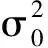
通过最小二乘求解海底应答器坐标以及观测值改正数:

(22)

分别计算单位权中误差和协方差阵:

(23)

式中:r为多余观测数;n为总观测数;t为必要观测数;QXX为平差参数的协因数阵。

3 算例分析

3.1 仿真算例分析

使用自主研发的水下声学定位仿真系统V1.0[19]生成了针对浅海和深海基准点的模拟GNSS/A观测数据。设应答器水深分别为100 m和3 000 m,如图3所示,采用组合航迹模拟海面测量载体进行GNSS/A观测时在海面的运动轨迹,即先进行多折线往返走航,后进行圆走航,模拟船速为2 m/s,采样间隔为8 s和12 s,并模拟海面波浪起伏对海面测量载体的影响,对换能器Z方向坐标加上2 m的余弦波动。

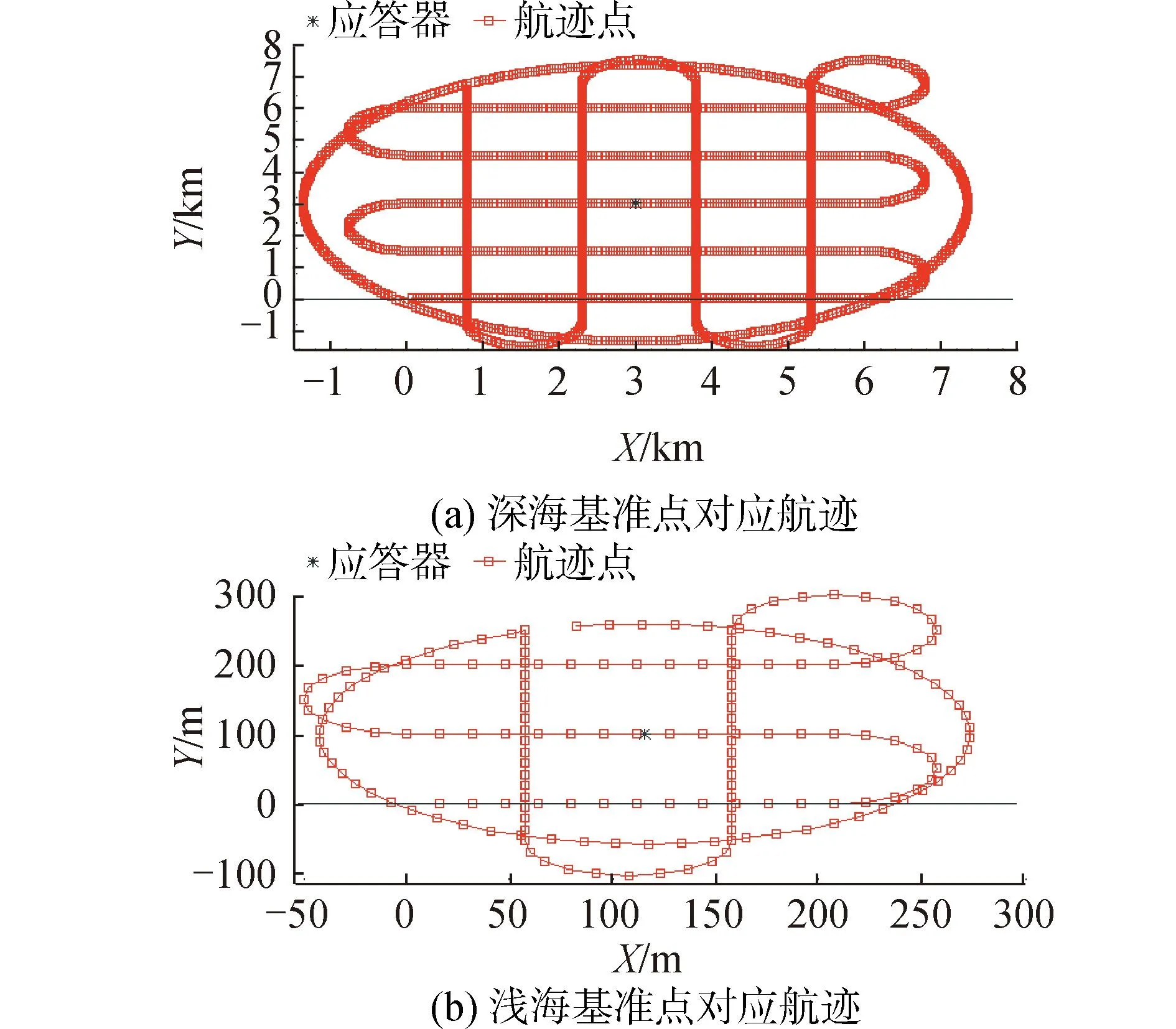
图3 组合航迹与应答器位置示意Fig.3 The diagram of combined surveying track and transponder′s position

浅海、深海对应组合航迹设置参数见表1。如图4所示,声速剖面采用Munk理想声速剖面,表层声速为1 548 m/s,根据声速剖面、换能器深度和应答器深度计算加权平均声速值[20]。2种走航观测各历元的声线入射角如图5所示。采用等梯度声线跟踪方法[21]计算换能器至应答器之间的声学仿真观测时间。

表1 组合航迹参数Table 1 Parameters of combined surveying track

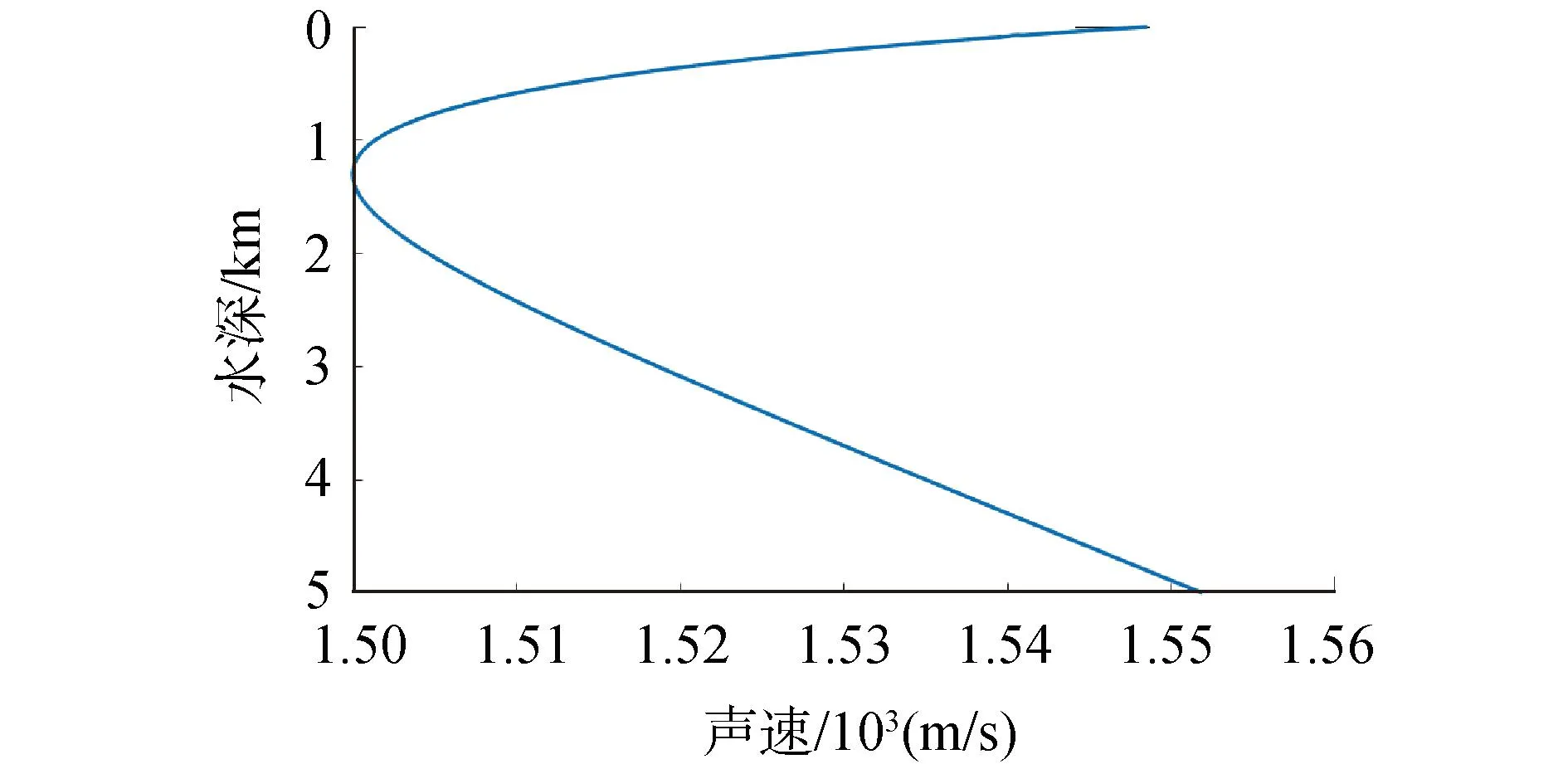
图4 Munk声速剖面Fig.4 Munk sound velocity profile

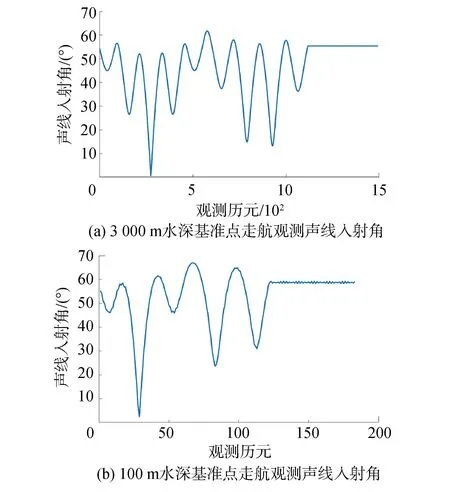
图5 模拟走航声线入射角示意Fig.5 The diagram of acoustic ray incident angles for simulated surveying

系统误差采用经验公式:

δρv=c1δρk+c2δρs+c3δρl+c4δρz

(24)

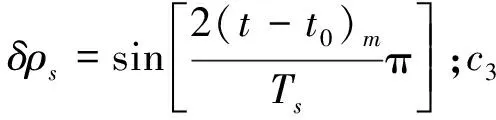
随机误差方面,设声学测距随机误差为5 cm,换能器坐标平面中误差为5 cm,垂向中误差为10 cm。

采用上述的模拟走航观测策略,使用水下声学定位仿真系统V1.0生成仿真声学观测值,仿真次数为500次,使用基于单程声径的水下非差定位方法(单程非差法)、基于单程声径的水下差分定位方法(单程单差法)、基于双程声径的水下非差定位方法(双程非差法)和本文提出的考虑双程声径的水下差分定位方法(双程单差法)分别对3 000 m、100 m水深海底应答器进行定位解算,所得精度结果如图6、图7所示。

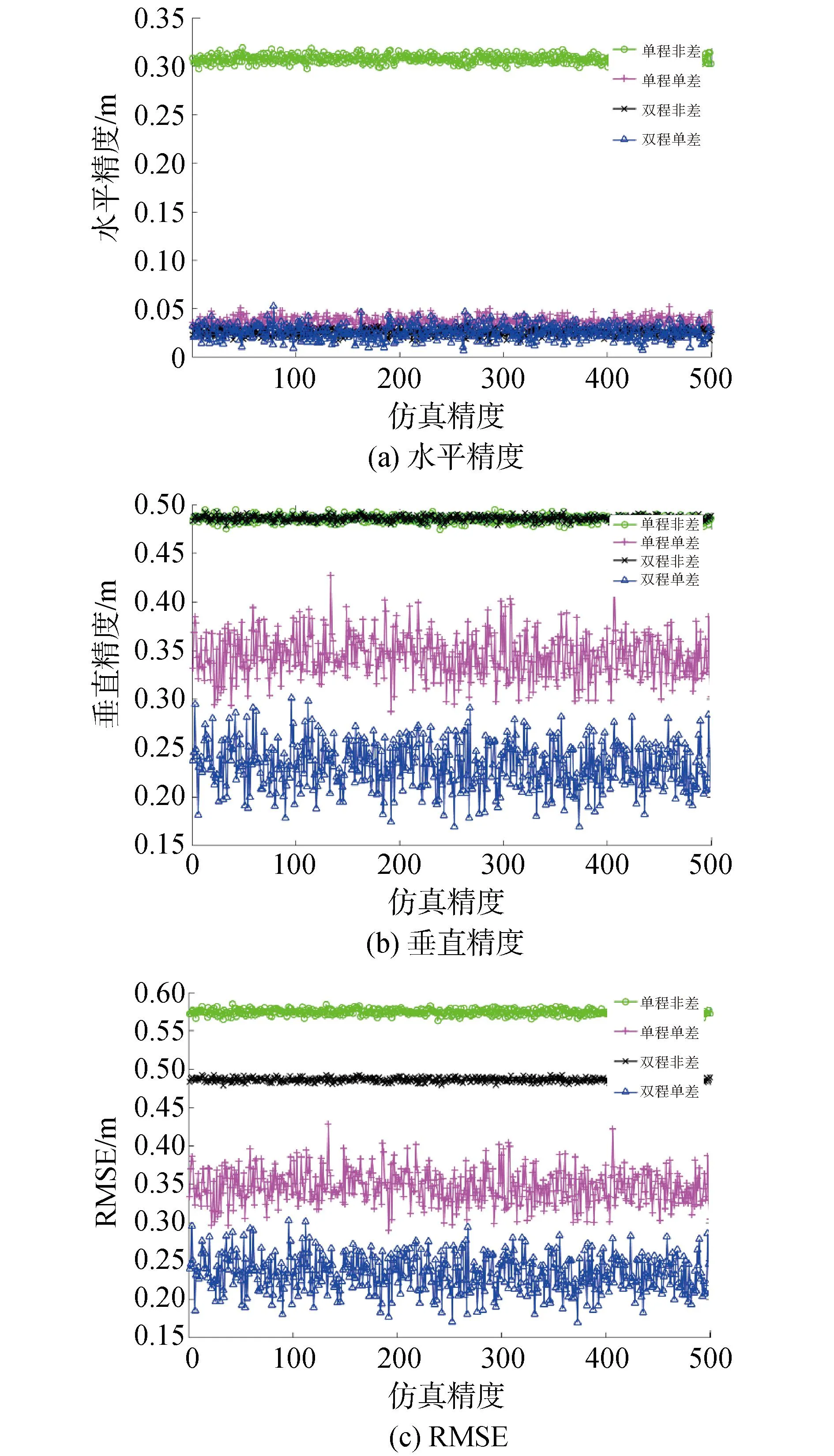
图6 3 000 m水深定位精度对比Fig.6 Comparison of positioning accuracy for 3 000 m depth

图7 100 m水深定位精度对比Fig.7 Comparison of positioning accuracy for 100 m depth

使用单程非差法、单程单差法、双程非差法和本文提出的双程单差法分别对3 000 m、100 m水深应答器进行定位解算,并分别统计其平均定位精度,如表2所示。

表2 传统方法与新方法平均定位解算精度Table 2 Mean positioning accuracy of traditional and new methods m

由以上解算结果可以看出,鉴于走航式GNSS/A观测的特点,即海面测量载体在海平面按预设航迹对海底应答器开展声学观测,只能从应答器上侧而无法从应答器下侧获取观测值,导致垂直方向上观测结构相对较差,系统误差抵偿能力较弱,对比图6或图7水平精度和垂直精度示意图可知,4种水下定位方法得到的水平定位精度均明显优于垂直定位精度。

其次,如表2所示,在解算3 000 m水深应答器坐标时,本文提出的双程单差法水平方向平均定位精度为0.024 m,与单程单差法、双程非差法精度相当,优于单程非差法的0.308 m;垂直方向平均定位精度为0.233 m,优于单程非差法的0.486 m、单程单差法的0.351 m、双程非差法的0.486 m。从海底应答器定位均方根误差(root mean squared error,RMSE)角度来看,本文提出的双程单差法的RMSE为0.234 m,优于单程非差法的0.575 m、单程单差法的0.352 m、双程非差法的0.487 m,分别提高了0.341、0.117、0.252 m。

如图7以及表2可知,由于水深较浅,在解算100 m水深应答器的坐标时,测距声信号传播时间的量级较小,海面测量载体收发时刻位置差对定位的影响比解算深海应答器坐标时相对较小。因此,在浅海情况下,本文提出的双程单差法所能达到的定位精度与传统单程单差法近似相等,略优于2种非差方法,定位精度的提升效果并不显著。

3.2 实测算例分析

实测算例采用2019年7月于我国南海区域开展的“海洋大地测量基准与海洋导航新技术深海综合试验”数据,该试验区域水深为3 000 m左右,试验测量船只配备GNSS接收机、高精度姿态传感器、声速剖面仪以及海面长基线定位系统等仪器设备。本次试验在海底布设了若干应答器作为海底基准站,海面测量船对海底基准站实施连续的GNSS/A观测,采集GNSS数据、姿态数据以及测距声信号传播时延数据等,其中声信号传播时延为往返的双程时延,便于后续开展对基于双程声径定位模型的研究;同时采集了测量区域内若干位置处的声速剖面,在后续的研究中采用观测区域内声速剖面平均值,以减小声速结构时空变化造成的误差。

本算例针对试验中布设的5号海底应答器,海面测量船以多折线往返航迹对其进行了GNSS/A观测,测量船航迹以及应答器概略位置如图8所示,测量船航速约为1.83 m/s,即3.65 kn,共取得5 489个声学观测值,测量船在测距声信号下行-上行过程中平均位移约为11.63 m。

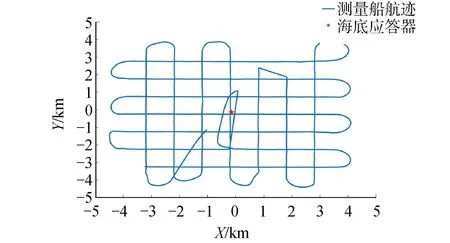
图8 走航观测航迹与应答器位置示意Fig.8 The diagram of surveying track and transponder′s position

如图9所示,本次试验在声学观测的同时进行了声速剖面的测量。走航观测各历元声线入射角如图10所示。

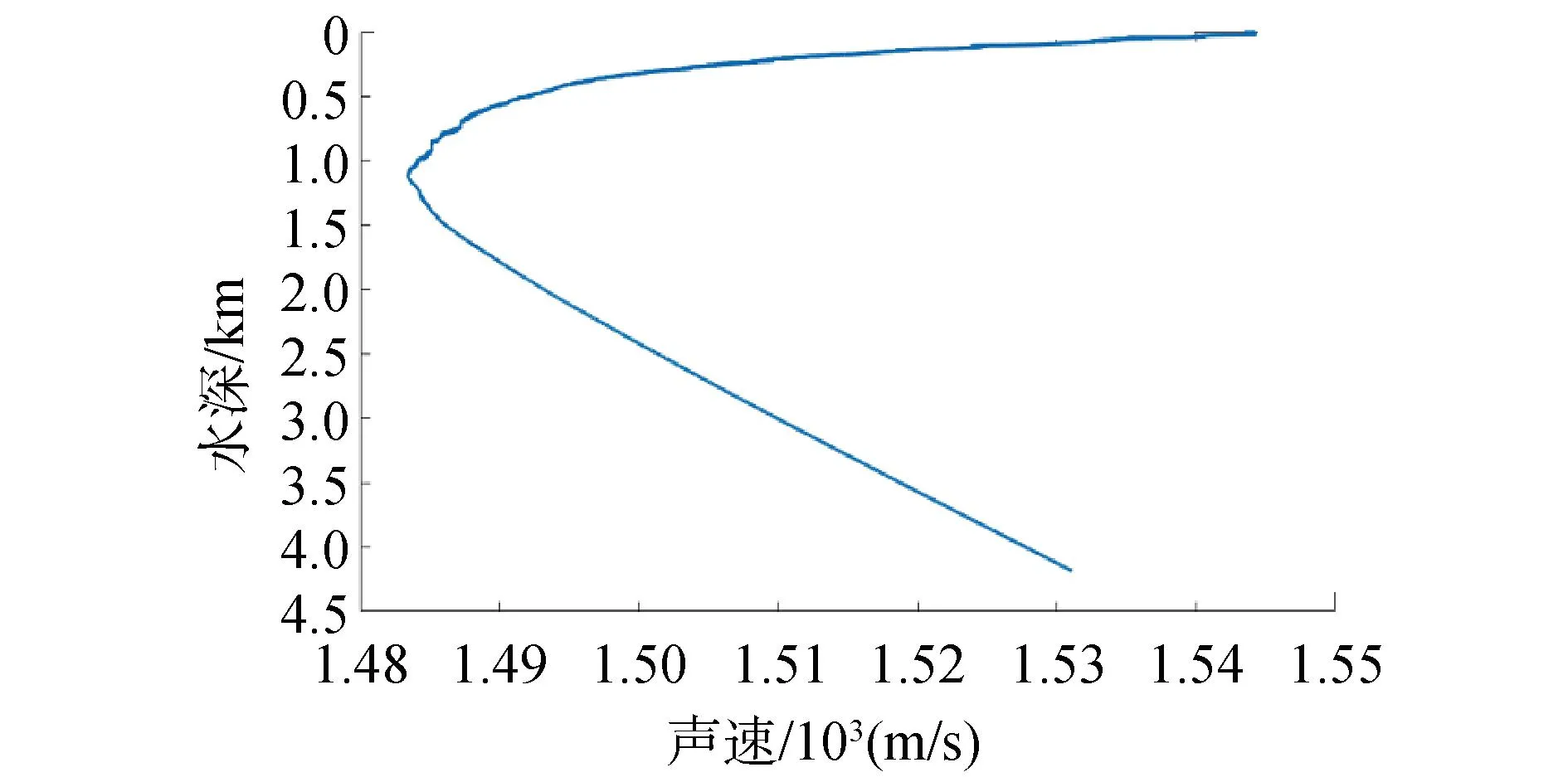
图9 实测声速剖面Fig.9 Measured sound velocity profile

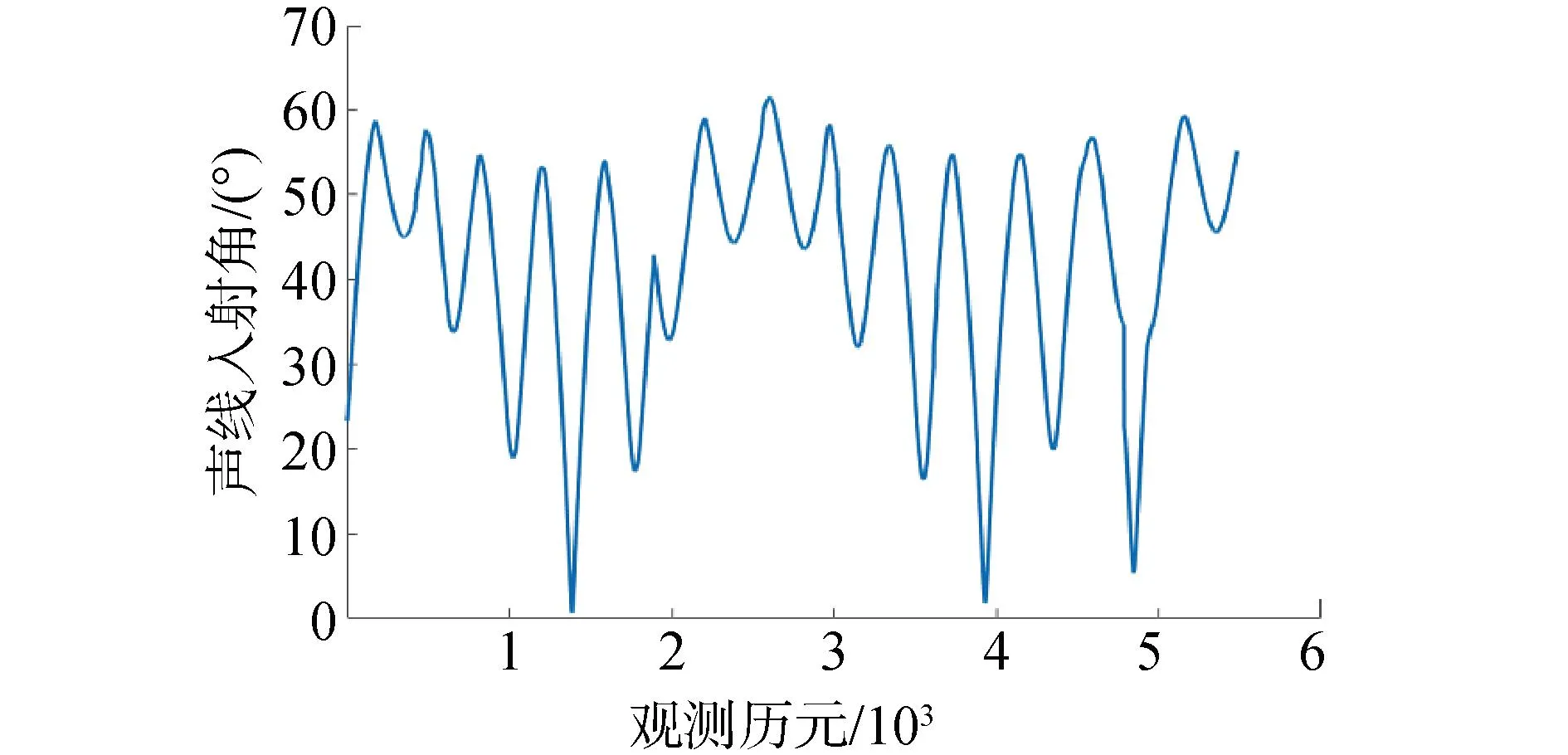
图10 声线入射角Fig.10 Acoustic ray incident angles

对原始观测数据进行换能器坐标转换、粗差剔除等预处理后,采用3.1节中的4种方法解算海底应答器的坐标,解算坐标及精度信息如表3所示,其中内符合精度为式(23)中协方差矩阵DXX对角线上各元素。

表3 定位结果统计Table 3 Statistical of positioning results m

从定位解算精度方面分析,本文提出的双程差分方法在水平方向上的内符合精度均优于其他3种传统定位方法,在垂直方向上,虽然差分方法会弱化观测结构,进一步抵消了观测值中的垂向信息,引起垂直方向定位精度降低,但是双程差分方法垂直方向的内符合精度相较于传统单程单差法提高了0.276 m。结果表明,本文提出的双程差分方法能够有效提高水下定位的精度,尤其适用于声线入射角变化明显的GNSS/A观测。

由式(22)可以得到观测值残差,如图11所示,2种非差方法得到的残差值波动幅度较大,单程非差法残差波动幅度约为-8～7 m,双程非差法残差波动幅度约为-9～5 m,可见非差方法无法消除因声速结构时空变化引起的系统性误差,残差曲线呈明显锯齿状;差分方法可以通过历元间差分运算抵消部分系统误差的影响,从图中可以看出,本文提出的双程单差法残差曲线波动幅度明显小于其他方法,波动范围约为-4～6 m,有效削弱了系统性误差。

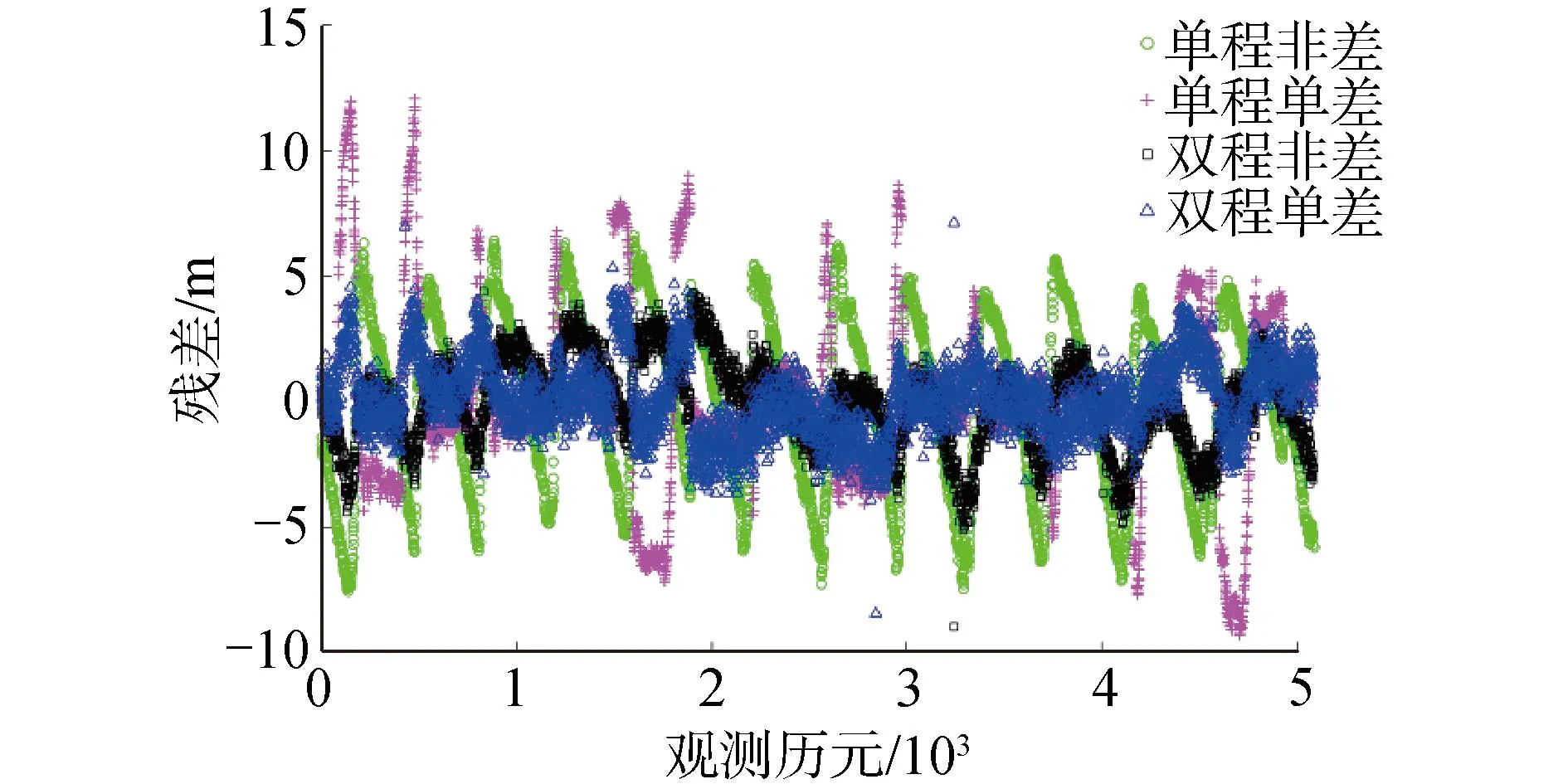
图11 不同方法对应的残差示意Fig.11 The diagram of the calculated residuals with different methods

如表4所示,分别计算4种方法的观测值残差统计特征,包括平均值、最大值、标准差和均方根误差。

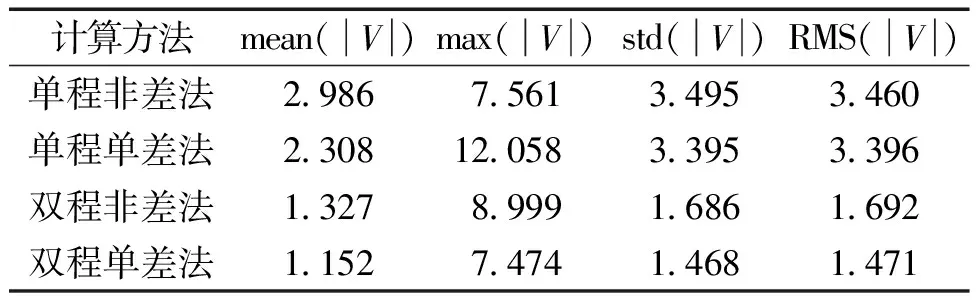
表4 残差统计结果Table 4 Statistical of positioning resultsm

从残差平均值角度看,本文提出的双程单差法残差平均值为1.152 m,比单程非差法提高了1.834 m,比单程单差法提高了1.156 m,比双程非差法提高了0.175 m;从残差均方根误差角度看,本文提出的双程单差法残差均方根误差为1.471 m,比单程非差法提高了1.989 m,比单程单差法提高了1.925 m,比双程非差法提高了0.221 m;本文提出的双程单差法其余的统计特征也均优于传统方法,说明本方法定位效果更优。

4 结论

1)在非圆走航观测中,测距声信号下行、上行路径长度绝大多数情况不相等,海面测量载体收发时刻位置差会对非差定位模型的定位精度产生一定影响,而考虑双程声径的水下定位模型则可以消除该误差的影响。本文提出的考虑双程声径的水下差分定位模型进一步通过历元间差分削弱其他若干系统误差的影响,进一步提高了水下定位的精度。

2)由于深海环境相较于浅海环境测距声信号传播时间的量级更大,更容易受到海面测量载体收发时刻位置差的影响,故本文提出的考虑双程声径的水下差分定位模型尤其适用于深海环境下的海底大地基准建设。

本文所提出的水下定位模型综合考虑了载体收发时刻位置差和系统误差对水下定位精度的影响,一定程度上提高了海底大地基准点的定位精度,具有一定的应用价值。但本文提出的模型未有效处理声线弯曲误差、声速结构时空变化误差等的影响,后续应结合声线跟踪等方法进一步改正声速误差,以获得更高的海底大地基准点定位精度。