基于SCA-VMD和排列熵的轴承故障诊断研究

蔡 俊,蔡士超

(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)

滚动轴承是机械设备中故障常发部件之一。设备运行时,磨损、疲劳、腐蚀、过载等原因都可能造成滚动轴承的局部损伤故障[1]。滚动轴承的故障率也越来越引起重视,不仅影响生产也容易导致重大安全事故。滚动轴承故障诊断的流程分为三部分:信号处理、特征提取和诊断识别,随着科学技术的发展,检测技术也不断的成熟,众多学者对轴承诊断的不断深究,在轴承故障诊断领域起到了很大的推动作用。若在故障的早期提前干预,可以很大程度上减少不必要的损失,在对轴承故障数据采集时得益于现在传感器的高精度,可以准确得到各个轴承运行状态的振动数据,并对振动信号做去噪处理,常见去噪算法有快速傅里叶变换(Fast Fourier Transform,FFT),小波包分解(Wavelet Packet Decomposition,WPD),变分模态分解[2]等,其中VMD在分解中可以很好解决各本征模态函数中出现的混叠现象。

使用经验模态分解(Empirical Modal Decomposition,EMD)用于处理非平稳信号的模态分解法,苏文胜等提出一种EMD降噪和谱峭度法的滚动轴承早期故障诊断新方法,根据互相关系数和峭度准则对采样信号进行EMD降噪[3],但EMD信号在分解信号的过程,本征模态间出现模态混叠、欠包络等问题。为更好的对信号分解降噪,得到能凸显故障信息特征的信号,郑义等人利用原始故障信号经优化变分模态分解后得到k个模态分量,筛选相关峭度最大的模态分量进行包络解调分析,提取故障特征[4]。

鉴于此,经验模态分解不能满足当前振动信号的去噪,对振动信号去噪使用VMD算法去除信号干扰,可以程度上保留振动信号的特征,并结合排列熵算法提取熵值并对各故障状态模态分量选取峭度值最大的四个模态分量,作为轴承故障诊断的特征样本集,最后结合人工蜂群算法优化支持向量积模型对轴承故障进行诊断,以此提高故障诊断的准确率。

1 基本理论

1.1 变分模态分解

VMD分解信号就是求变分最优解的过程,核心是对变分问题的构建与求解,在VMD的求解中需要满足每个模态分量的中心频率的带宽和最小。变分模态分解的参数选取对分解信号起到至关重要的作用,其中以模态个数与惩罚参数影响较大。

1.1.1 构造VMD约束变分模型

信号由k有个限带宽模态分量组成。首先,求各模态分量的单边频谱,调整各本征模态对应基频带;最后,估算各本征模态分量的带宽,构造约束变分模型如式(1)所示。

(1)

式(1)中,模态分量的集合为{uk}={u1,u2,…,uk}。

1.1.2 变分问题求解

对构造的约束变分模型求最优解。首先,引入拉格朗日乘子和二阶惩罚因子,将约束变分模型求解为无约束变分模型,以此求解每个变分模态分量,如式(2)所示。然后,采用交替乘子法不断更新各变量以及中心频率数值。通过计算式(3)-式(5),得到扩展拉格朗日的鞍点;最终求出无约束变分最优解。

(2)

(3)

(4)

(5)

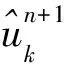
1.2 SCA优化VMD参数

由于VMD在分解信号时能把振动故障信号更好的分解在各个IMF分量上,在一定程度上避免出现模态混叠的现象。但因VMD分解效果受其自身的模态个数k与惩罚因数的选值的影响较大。针对数据本身的特性,使用SCA算法对其参数进行迭代,直至寻找最优组合。SCA算法是Seyedali Mirjalili等于2016年提出的一种新型智能算法正余弦算法[5]。该算法可以同时产生多个初始候选解,以正余弦的数学模型作为基础向不同位置产生波动,寻找并确定最优解的波动方向。通过不断地计算当前解的位置,以及搜索空间中的不同区域范围,并计算当前解的位置来解决局部最优问题,从而使得其解可以收敛于全局最优。算法公式如式(6)所示。

(6)

(7)

式(7)中,r1为当前解与最优解的位置区域范围,a恒等于2;T是最大迭代数;t是当前迭代数。

其参数寻优过程如下:

(1) 初始化参数、位置、迭代群体大小、k和α的取值范围。

(2) 根据公式定义r1,r2和r3的随机值,把最小平均包络熵设置为适应度函数值。

(3)通过公式(6)不断地迭代寻优,将每次迭代的最优值及其对应的参数k和α保存。

(4)迭代至最大次数,终止迭代,保存当前最优值。

1.3 排列熵

排列熵(Permutation Entropy,PE),作为近几年发展起来的一种检测信号突变的新方法[7]。PE与近似熵、样本熵等是对时间序列复杂程度的衡量指标。与近似熵相比,样本熵对数据长度的依赖性减少,抗干扰能力增强,已经广泛应用于脑电波信号和振动信号等研究中[8]。而排列熵在计算子系列的复杂程度时,能够将排列的思想引入到抗噪声处理中,具有较好的表现,并且只需要较短的时间序列就可以得到稳定的系统特征量。排列熵具有良好的鲁棒性以及对信号变化敏感的优点,常用来分析自动化机械设备运行状态[9]。排列熵的公式如式(8)所示。

(8)

式(8)中,πj1,j2,…,jm是重构向量的排列模式,y为时间序列。

2 轴承故障诊断研究

故障诊断模型采用优化VMD参数并结合PE的方法来提高故障诊断的准确度,诊断流程图如图1所示。

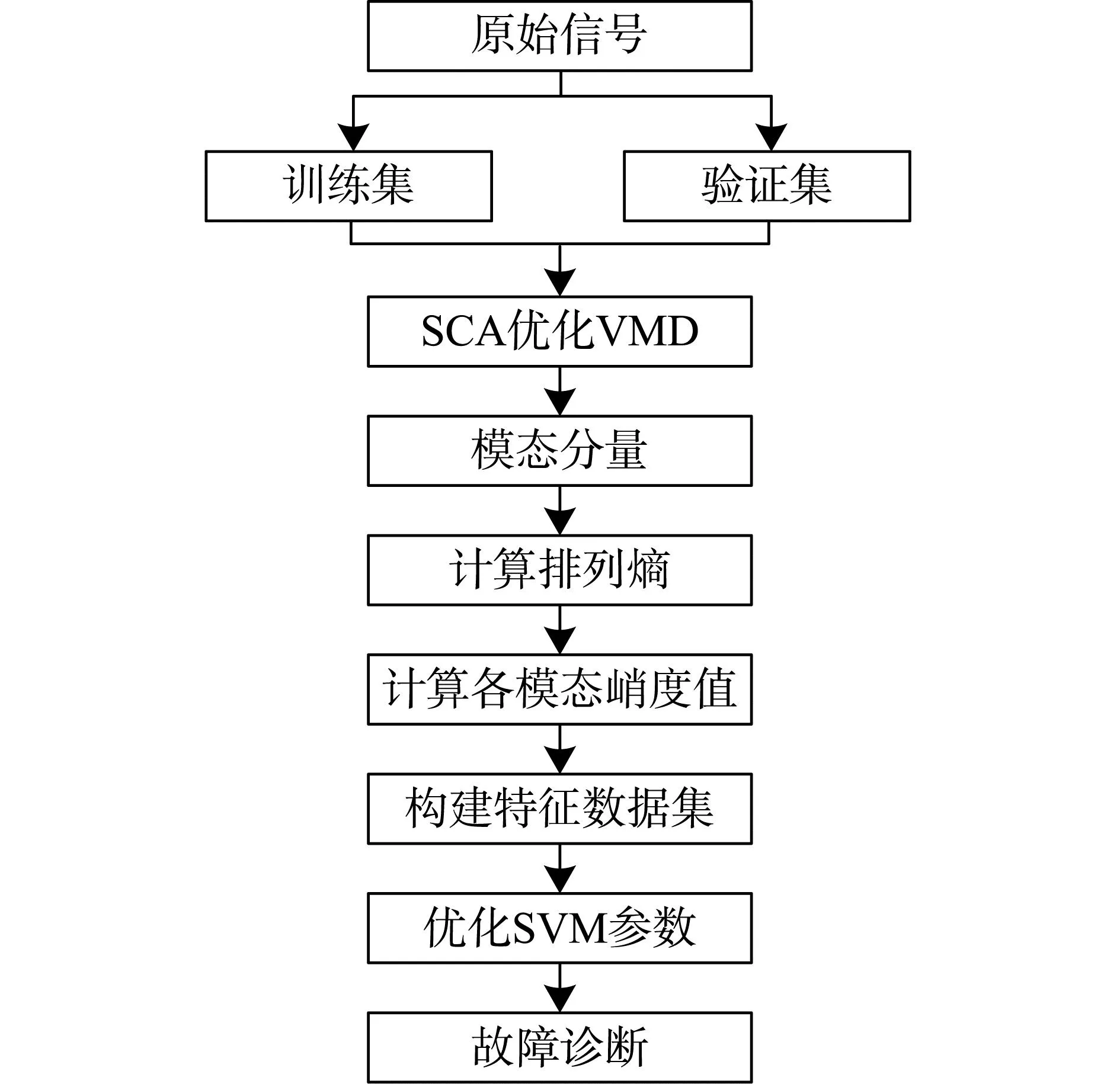
图1 轴承故障诊断模型

根据图1的故障诊断模型,首先,对不同轴承故障类型进行VMD参数优化,得到振动信号特征最优组合的k与α的值,对信号进行分解,对信号中的噪声能很好的消除。然后,构建特征向量矩阵,通过排列熵计算重构后的模态分量并对筛选出峭度值最大的四个模态进行分类;运用该方法降噪后,VMD的分解信号的能力提到提升,实现有效的故障特征提取。最后,故障诊断阶段把计算后特征数据集分为训练集与验证集输入到优化后的支持向量积模型中进行故障识别。

3 实验验证

3.1 实验数据

轴承故障振动数据使用西储大学官方数据库进行实验分析。电机转速为1797r/min,采样频率12kHz,轴承的故障尺寸分别为损伤尺寸a:0.007inch、损伤尺寸b:0.014inch及损伤尺寸c:0021inch三种轴承损伤直径。实验中将轴承故障类型分为滚动体、外圈、内圈故障,正常四种类型。为了提高轴承运行故障诊断的准确率,在数据集构建中,把同一故障不同损伤尺寸构建特征数据集,每类故障选取三种不同损伤程度的样本数据进行数据融合,其中,每一种损伤尺寸40组样本,采样点数为1024。为更好的模拟真实工况的情况,对每类故障中的样本进行打乱。通过对轴承不同故障类型的时域波形图进行对比,分析每类故障的特征,如图2所示。具体实验数据说明见表1。

表1 实验数据集表

图2 轴承状态时域图

将不同轴承故障类型的时域图与正常状态时的信号对比,得出当轴承发生故障时振动信号特征表现不明显,振动幅值变化很大,有效的振动信号被湮没,若是不采用高效的特征提取的方法去除信号中噪声,故障诊断模型的准确率无法提高。

3.1.1 故障特征提取

以轴承内圈故障数据研究为例,对比EMD与VMD的频域图分析,得到不同模态的频谱图,如图3所示,EMD在分解故障信号时各本征模态间出现模态混叠现象,各模态分量中噪声没有去除,而图4中,VMD分解得到各频率部分很好的分布在各本征模态分量中,利用排列熵来定量确定VMD分解后信号的含躁程度[9],得到信噪比较高的信号,利于提高故障分类精度。

图3 EMD频域图

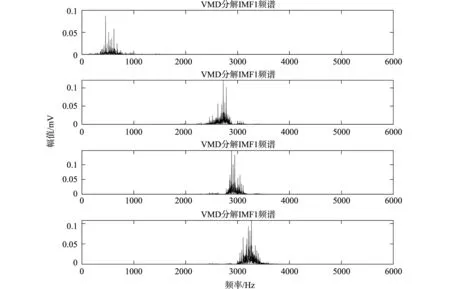
图4 VMD频域图

由图3和图4频域分解图可得VMD算法较EMD算法具有很好的抗模态混叠特征,但VMD在分解信号受参数影响,为此在分解原始信号时,为减少原始信号特征的丢失,α和k的取值决定了该算法分解信号的性能,图4中VMD的参数取α=2000,k=4,若在处理信号前利用寻优算法对VMD参数优化,能达到最佳的分解信号的效果[10]。

经上述的分析,VMD分解能力受参数的影响,将使用SCA算法对VMD参数优化并迭代50次,以此得到最优VMD参数,以内圈故障为例对VMD进行参数优化。如图5所示。

图5 SCA算法参数寻优

SCA算法寻优VMD参数时,适应度函数值越低,代表IMF分量中噪声含量越少,在多次迭代过程中适应度值都未发生变化,表明此时的VMD参数得到最优值。VMD经过寻优算法SCA优化后,可以有效的避免分解信号中出现模态混叠现象。此次实验中得到不同轴承故障SCA-VMD最优参数组合[k,α],在选取适应度函数时,选取迭代中最小的适应度函数,最优参数组合分别为滚动体故障[6,1812.57],内圈故障[7,2143.68],正常状态为[5,1697.72]和外圈故障为[7,1702.36]。

将SCA优化得到的最优参数组合与变分模态分解模型结合后,为更好的提取振动信号中的有效信息,使用排列熵重构本征模态分量并构造低噪声特征矩阵,计算该特征矩阵的峭度值,峭度值越大其包含的振动冲击越明显。表2为计算排列熵后各本征模态的峭度值。根据表2筛选峭度值最大的四个本征模态分量,构建新的特征数据集,再进行故障分类。

表2 本征模态峭度值

*U[1]-U[7]为各故障类型的本征模态分量经过计算峭度得到的值。

3.2 故障分类模型

轴承故障信号具有非平稳特性,故障特征并不明显,在实际工业生产中不能获取大量的故障数据,故本文采用对非线性小样本数据中有很好分类效果的支持向量积(Support Vector Machine,SVM)。SVM是经典的分类算法,而单一的SVM算法难以满足精度要求[11]。实验结果表明,SVM在故障诊断时内核函数中参数g与c对诊断精度影响很大。笔者采用人工蜂群算法(Artificial Bee Colony,ABC)对SVM参数g与c进行优化,通过个体的局部寻优到群体的全局寻优,收敛速度更快。实验中取30%样本集作为测试集,特征数据集使用未经参数优化VMD-PE组合与经过参数优化SCA-VMD-PE组合,分别输入到ABC-SVM诊断模型中对轴承故障进行预测,结果如图6、图7所示。

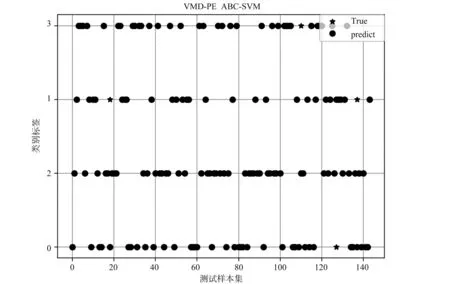
图6 未优化VMD参数诊断结果

图7 优化VMD参数诊断结果

构建测试样本集时,通过选取峭度函数值最大的四组模态分量,将其输入到故障诊断模型中,可以得到更好的故障分类的结果,根据图6、图7实验结果可以得出,对比未优化VMD参数与优化VMD参数。从分类诊断的结果中发现,未优化的测试样本集中,除滚动体标签0外,其他三处中,分别存在预测值有误差,而经过优化的测试样本集,预测值误差只出现一处,进而验证本文提出的SCA算法对VMD的分解信号能力的优化,有利于轴承振动信号在细微故障处的特征提取。本文提出融合不同损伤程度的原始数据集,再经SCA算法优化VMD参数,筛选出峭度值最大的模态分量,构造特征数据集的方法,能在实际生产过程中很好的解决轴承运行状态的故障单一化。

为更充分的验证本文提出的方法对分解信号的优越性能,提出了以下验证方法,将不同诊断模型做分类结果对比,分为四组对照实验,实验一:VMD-PE-SVM,这里的支持向量机经过K折交叉验证;实验二:VMD-PE-ABC-SVM;实验三:SCA-VMD-PE-SVM;实验四:SCA-VMD-PE-ABC-SVM。对比结果如图8所示。

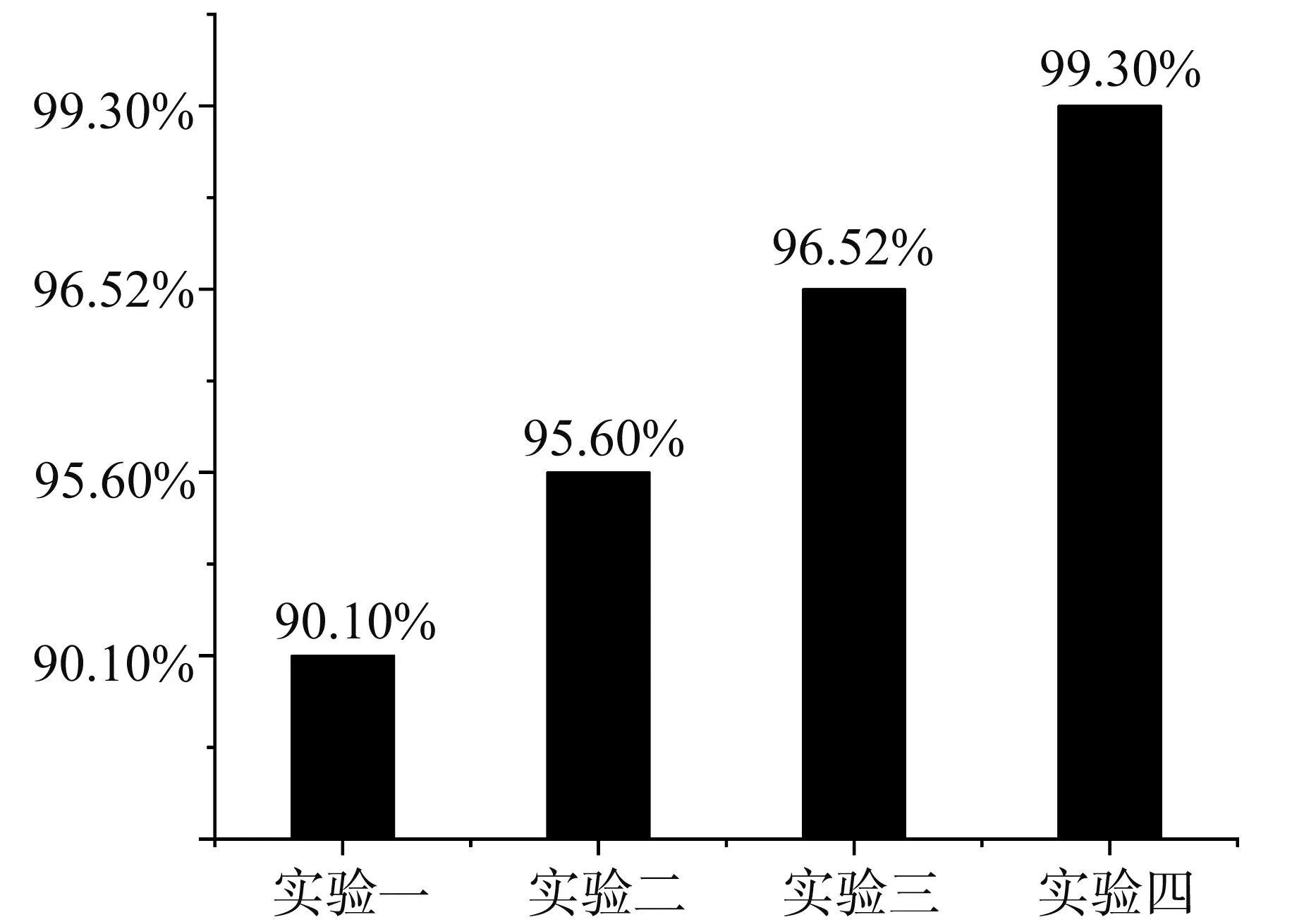
图8 对照实验结果图

实验一与实验二中都未对VMD参数进行优化,但不同在于SVM通过ABC算法优化其参数,准确率提高5.5%;因此在故障分类诊断中,优化分类器对实验准确率会有很好的提升;实验一与实验三进行对比,实验三中优化VMD参数k和α,准确率比实验一提高6.42%,进一步验证了优化VMD参数对故障分类准确率的影响;最后,实验二和实验四进行对比,充分说明本文提出的方法,在对轴承故障的特征提取以及故障分类中效果显著。本文提出的SCA-VMD-PE-ABC-SVM的方法在故障诊断中准确率达到99.3%。

4 结论

在工业生产中早期设备轴承故障信号微弱,针对同种故障可能存在不同损伤尺寸,通过构建同种故障类型中含不同损伤尺寸的特征数据集,提出了基于SCA-VMD和排列熵的轴承故障诊断研究方法。

首先,采用SCA算法对VMD寻找各故障类型最优的参数组合,并计算各故障类型模态分量的PE值和峭度值,筛选包含冲击信息的本征模态分量,构建特征向量样本集;其次,把样本集输入到诊断模型ABC-SVM分类器中,对轴承故障类型进行诊断准确率为99.3%;最后,根据四组对比实验分析,结合VMD-PE与SCA-VMD-PE提取特征构成样本集的诊断结果,分析得出不同特征提取方法影响故障诊断的准确率。