一种抗替换攻击的SM2签名算法

严都力，薛李波，杨龑栋，刘 翼，延照耀

（1.延安大学 数学与计算机科学学院；2.延安大学 石油与环境工程学院，陕西 延安 716000）

SM2椭圆曲线公钥密码算法［1］是中国自主设计的公钥密码算法，具有存储空间小、签名速度快等优势，被广泛用于教育、社保、金融、交通、公共安全、国防工业等重要领域。相关研究成果表明，虽然中国自主设计的国产密码是实现信息系统安全可控的核心保障，但在使用过程中也将遭受一系列不同动机的分析和攻击［2］。

算法替换攻击［3-4］的主要攻击对象是密码算法本身，攻击者在密码算法设计或实现过程中加入一些仅自己可知的秘密信息或陷门信息，即在密码算法中设置陷门，用一个被嵌入陷门信息的算法来替换原诚实算法，攻击者即可在用户不知情的情况下窃取其密钥信息［5-6］。替换攻击最早起源于SIMMONS［7］提出的阈下信道，通信双方借助密码学技术构建隐藏通道，隐藏传输的秘密信息。随后，YOUNG 等［8］对RSA 加密、Diffie-Hellman 密钥交换、ElGamal 签名等算法给出了具体的攻击方法。2015年，BELLARE等［9］给出了替换攻击的形式化定义和安全模型。DEGABRIELE 等［10］克服了BELLARE 安全模型中设置攻击者替换攻击能力限制的局限性，提出了适用范围更广泛的输入触发替换攻击。LIU等［11］研究了可拆分的特殊签名体制的替换攻击，攻击者所持有的秘密后门信息无需嵌入替换算法便可提取签名私钥。JOONSANG 等［12］研究了DSA［13］签名算法的替换攻击，并给出了具体的颠覆方法和抵抗用户利用签名时间分析检测颠覆攻击的对策。BELLARE等［14］提出了参数颠覆的概念，并分析了非交互式零知识证明协议在公共参考串模型下遭受替换攻击的安全性。DODIS 等［15］和DEGABRIELE 等［16］基于参数颠覆研究了伪随机数生成器的替换攻击问题。黄欣沂等［2］以中国商用密码SM2的数字签名算法和公钥加密算法为分析对象，提出两种高效难检测的密钥渗漏攻击。此外，国内外学者围绕对称加密、数字签名、密钥协商协议和零知识证明系统等不同密码算法深入的开展了后门攻击评估［17］。

随着各种替换攻击事件的不断曝光，如何构造抵抗替换攻击的密码算法，已经成为密码学界备受关注的一个热点问题。目前已有相关研究学者提出了一些替换攻击的方法，BELLARE等［18］和ATENIESE等［19］分别设计了唯一密文和唯一签名方案的防御措施来抵制替换攻击。RUSSELL 等［20］基于检测安全思想提出了直接检测并抵制算法替换攻击的看门狗（Watchdog）安全模型。RUSSELL 等［21］基于分割融合技术，提出了一种对随机化密码算法的替换攻击防范方法。MIRONOV等［22］提出了一种功能保留、安全保留、抗泄漏的密码逆向防火墙（Cryptographic reverse firewall，CRF）来抵御颠覆攻击。FISCHLIN等［23］提出了区别于CRF 与Watchdog 防御机制的自防御方法，同时为随机化单钥加密体制和具有同态性质的公钥加密体制设计了相应的安全防护方法。康步荣等［24］提出了抵抗随机数后门攻击的密码算法，并对已有的抗随机数后门攻击密码算法进行了总结和梳理。中国自主设计的国产商用密码是实现信息系统安全可控的核心保障，虽然文献［2］提出了针对SM2 签名算法的秘钥渗透攻击，但尚未给出具体抗替换攻击方案。基于文献［2］，在一般群模型下，本文设计了一种抗替换攻击的SM2 签名算法，主要研究内容如下：

1）刻画了针对签名算法的替换攻击模型，攻击者利用这一攻击方法能够达到秘钥提取和不可检测性两种安全目标；

2）利用哈希函数将签名私钥、签名消息与其随机数的哈希结果作为签名的随机组件，对原始的SM2 签名算法改进，在一般群模型下，构造具备抗替换攻击的SM2 签名方案，即使攻击者替换原始SM2 签名算法某些组件得到有效签名，也无法获得签名私钥的任何信息；

3）将抗替换攻击的SM2 签名算法与原始SM2签名算法进行效率测试，实验结果验证了抗替换攻击的SM2签名算法的可行性。

1 预备知识

1.1 哈希函数

定义1［25］一个安全的密码学哈希函数h：{0，1}*→{0，1}n，满足以下性质：

1）抗碰撞性：找到2 个不同输入M与M′，满足h(M)=h(M′)在计算上是不可行的；

2）抗原像性：给定y=h(M)，对于概率多项式时间敌手找到一个M′，使得h(M′)=y在计算上不可行；

3）抗第二原像性：给定输入M，对于概率多项式时间敌手找到一个M′(M′≠M)，使得h(M′)=h(M)在计算上是不可行的。

1.2 伪随机函数

定义2［26］函数F：{0，1}λ×{0，1}ρ→{0，1}n记作一个有效的带密钥函数，函数表示所有f：{0，1}ρ→{0，1}n函数的集合。如果对所有概率多项式时间区分器D，存在一个可忽略的函数ε(λ)，满足：

则称F是一个伪随机函数（Pseudorandom function，PRF）。区分器D、区分函数F与f优势定义为

1.3 SM2签名算法

SM2 签名算法是基于椭圆曲线的公钥密码算法，SM2 包含加解密算法、数字签名算法和密钥交换协议。定义SM2=(KeyGenSM2，SignSM2，VeyifySM2)为原始的签名方案。选择一个256 位素数域E(Fq)上的椭圆曲线，其参数定义为pp={q，Fq，a，b，G，n，Hv，f，ZA}，其中p为Fp特征，参数a，b∈Fp确定了安全的椭圆曲线E(Fp)：y2=x3+ax+b，任意选取基点G=(xG，yG)，其中G≠O，O表示椭圆曲线上的无穷远点，素数n表示基点G的阶；h：{0，1}*→Zn表示哈希函数，Hv：{0，1}*→{0，1}256表示消息长度为vbit 的哈希函数，在SM2 签名算法中v取值为256；f：→Zn表示将椭圆曲线上的坐标点转化为整数；ZA=Hv(ENTL||ID||a||b||xG||yG||xP||yP)表示签名身份标识与系统参数的哈希值，ENTL由2个字节标识的ID的bit 长度，ID为用户身份标识，xG、yG为基点，xP、yP为用户的公钥。SM2签名算法描述如下：

1）秘钥生成算法（KeyGenSM2）

①签名者任意选取整数d，其中1 ≤d≤n；

② 计算P=dG=(xP，yP)，P表示签名公钥，d表示签名私钥。

2）签名算法（SignSM2）

② 计算e=h()；

③任意选取随机数k∈[1，n-1]，计算kG=(x1，y1)；

④ 计算x1=f(kG)；

⑤ 计算签名r=(e+x1)modn，若r=0 或r+k=n，则重新选择随机数k；

⑥ 计算签名s=(1+d)-1⋅(k-rd)modn，若s=0，则重新选择随机数k；

⑦ 输出消息M的签名σ=(r，s)。

3）验证算法（VerifySM2）

①验证者收到任意消息M的签名σ=(r，s)，利用系统参数和签名公钥对签名σ=(r，s)验证是否有效；

② 验 证r∈[1，n-1]和s∈[1，n-1]是否成立，若不成立，则验证不通过；

④ 计算e=h()；

⑤ 计算t=(r+s)modn，若t=0，则验证不通过；

1.4 一般群模型

一般群模型［27］是一种理想的安全模型。在该模型中，敌手只能访问一个群中经过随机编码后的元素，而非实际的元素，系统外部用户即使知道群中的元素也必须访问群预言机，预言机模拟群运算。预言机以2 个经过随机编码的元素作为输入，输出则是第三个经过随机编码的元素。与随机预言机模型类似，敌手自身不能进行群运算，必须以经过随机编码的元素向预言机查询，以获得经过随机编码的运算结果。

定义3［27］假设存在两个同构群G1、G2，在一般群模型中，设ζ是一个编码函数，一个预言机O 模拟群G1上的运算，即：给定两个元素∈G1和两个整数e1和e2，O计算F3=e1F1+e2F2，并返回

2 替换攻击模型

替换攻击指攻击者在密码算法设计或实现过程中时设置一些仅自己可知的陷门信息，用一个被嵌入陷门信息的算法来替换原始诚实算法，攻击者即可在用户不知情的情况下窃取其密钥信息，替换攻击的形式化定义如下。

定义4［5］SS=(KeyGen，Sign，Verify)记为原始签名方案，攻击者通过某种手段破坏SS，得到替换后的签名方案具体算法描述如下：

替换后的签名方案需满足正确性要求，即

替换签名方案除满足正确性要求外，还需同时满足“密钥提取”和“不可检测性”。其定义如下：

密钥提取（KeyExtract）：正常情况下，攻击者从原始签名中分析获得签名私钥是计算上不可行的。假设存在攻击者A 可通过在签名方案中嵌入陷门信息，提取签名私钥或签名中其他秘密信息，A首先需要对原始签名进行替换获得有效的替换签名，然后利用若干个替换后的签名与替换密钥提取签名私钥，这类攻击是当前最为普遍的替换攻击方式，又被称颠覆攻击。其形式化定义如下：

定义5［5］SS=(KeyGen，Sign，Verify)记为原始签名方案记作被嵌入陷门信息替换后的签名方案，A 为概率多项式时间敌手，C 定义为挑战者，A 提取密钥游戏定义为

1）初始化：C 执行KeyGen(1λ)与算法，生成正常签名密钥对(pk，sk)和替换密钥subk，C将公钥pk发送给A；

2）签名询问：A 任意选择消息mi进行签名询问，C将mi的签名应答给A；

A 成功提取密钥的优势定义为安全参数λ的函数：

不可检测性（detect）：该安全目标从敌手A的视角定义，一般情况下拥有签名私钥的用户对检测替换签名更加感兴趣，即在不可检测性定义中，用户被赋予拥有签名私钥能力的检测者来检测签名。对于没有替换密钥的用户，他们无法检测签名是正常签名算法还是替换后的签名算法生成的签名。用户与挑战者之间刻画检测替换签名的游戏定义为

1）初始化：挑战者C 执行KeyGen(1λ) 和算法生成原始签名密钥对(pk，sk)和替换密钥subk，C将公钥pk发送给D；

2）训练：D询问C关于消息mi的签名，C将对应的签名σi返回给D；

3）挑战：D输入消息mi，C选择b∈{0，1}，若b=0，C执行σi=Sign(sk，mi)，得到签名σi作为应答，否则，C执行将作为应答；

4）猜测：D 输出一个b′，如果b′=b，D 检测替换签名成功。

3 抗替换攻击的SM2签名算法

根据文献［2］对SM2 签名算法的替换攻击，攻击者在攻击前，运行密钥生成算法生成替换密钥subk，然后借助密码杂凑函数Fκ计算随机数ki。被篡改后SM2签名算法与原始SM2签名算法区别在于随机数k的选择，ki为第i次运行被篡改SM2 签名算法所使用的随机数，该攻击方法最终达到秘钥提取和不可检测性安全目标，详细攻击方案及安全性分析见文献［2］。

为了抵抗攻击者对SM2 签名算法的替换攻击，对SM2 签名算法进行改进，借助哈希函数和签名私钥计算签名中辅助随机数α=h(d||M||k)，其中，d是签名私钥，M是签名消息，k为随机数。针对不同签名消息m计算得到不同的α，且α只能被签名者计算，然后将α作为签名组件应用于生成签名。签名中辅助随机数α的计算与签名消息M、签名私钥d绑定目的为了保证α值的唯一性。由于改进后的SM2签名方案中使用的辅助随机数α由特定方法计算，即使攻击者尝试通过替换k达到攻击目的，签名者也可以通过计算和判断α来确定是否继续执行签名算法。若签名者计算α=h(d||M||k)，则继续执行签名算法；否则，终止。此判断过程保证了签名算法中使用的随机数α的正确有效性，抗替换的SM2签名方案描述如下。

1）密钥生成算法（KeyGenSM2）

①签名者任意选取整数d，其中，1 ≤d≤n；

② 计算P=dG，P表示签名公钥，d表示签名私钥。

2）签名算法（SignSM2）

② 计算e=h()；

③ 任意选取随机数k∈[1，n-1]，计算α=h(d||M||k)；

④ 计算αG=(x1，y1)；

⑤ 计算x1=f(αG)；

⑥ 计算签名r=(e+x1)modn，若r=0 或r+k=n，则重新选择随机数k；

⑦ 计算签名s=(1+d)-1⋅(α-rd)modn，若s=0，则重新选择随机数k；

⑧ 输出消息M的签名σ=(r，s)。

3）验证算法（VerifySM2）

①验证者收到任意消息M的签名σ=(r，s)，利用系统参数和签名公钥对签名σ=(r，s)验证是否有效；

② 验 证r∈[1，n-1]和s∈[1，n-1]是否成立，若不成立，则验证不通过；

④ 计算e=h()；

⑤ 计 算t=(r+s)modn，若t=0，则验证不通过；

⑦ 计算x1′=f(sG+tP)；

4 安全性分析

4.1 正确性分析

由s=(1+d)-1⋅(α-rd)modn、t=(r+s)modn和P=dG得

4.2 抗替换攻击性

定理1假设攻击者A 在概率多项式时间qt内，经过qs次签名询问得到两个连续有效的抗替换攻击SM2 签名，A 利用密钥提取的方法提取出私钥d的概率是可忽略的。

证明若攻击者A获得任意两个连续消息Mi-1和Mi的替换攻击SM2签名，分别为和，A按照秘钥提取方法提取签名私钥：

①计算ki=Fκ([ri]G)；

②计算αi=h(d||Mi||ki)；

③依据等式si=(1+d)-1⋅(αi-rid)modn；

⑤ 判断d′=d是否成立。

上述步骤②等式中，因αi=h(d||Mi||ki)中d是签名私钥A 未知，A 无法计算出αi，即使A 已知其他签名组件信息，也无法继续计算得到d′，更无法判断d′=d是否成立，所以A 提取私钥d失败。此外，即使可以替换每个抗替换攻击SM2 签名中使用的随机数ki，当A获取x个有效签名，其中x≤qs：

根据以上方程式，敌手A 已知签名Mi、ri、si和ki，但A 仍然无法在概率多项式时间内计算签名中的αi，x个方程等式中有x+1个未知数，A 无法通过已知签名信息提取出签名私钥d。

综上得证，攻击者A 利用密钥提取的方法提取签名密钥d的概率是可忽略的，证毕。

4.3 存在性不可伪造

定理2若h是均匀一致且抗碰撞的哈希函数，f是几乎可逆的函数，则抗替换攻击的SM2 签名方案在一般群模型下是满足自适应选择消息攻击下存在性不可伪造。

证明假设攻击者A 不能直接访问双线性群的元素，而只能通过与预言机O 交互获得群元素的随机映射的像，群运算由预言机O 执行，攻击者可以通过访问预言机O 获得新的群元素。敌手可以从公钥或者签名预言机查询中获取群元素句柄。实际上，A 可以使用公钥中的句柄和签名作为“基础”来执行进一步的群操作。

令(G，P)是公钥中的群元素句柄是签名查询中创建的群元素句柄，qs表示签名查询询问的次数，根据假设A 想要计算的所有群元素都有一个表单其中，是A 随机选择的已知整数，因此，可以通过以下方式统一群操作查询系数向量(z1，z2，…，例如，将基本元素G乘以整数z可以表示为一个群操作查询(z，0，…，0)。

假设存在一个概率多项式敌手A，存在挑战者C模拟A 的攻击环境，使A 的优势可以忽略不计。为了回答A 的群操作查询，挑战者C 将用一个L来记录群查询操作中生成的信息。挑战者C首先选择基点G，将(1，G，-，-)添加到列表L中，然后随机选择一个整数d∈Zn，计算P=dG，将(d，P，-，-)添加至L列表中，设qs表示敌手A 进行签名询问的次数，qc表示C 与A 交互过程中当前进行签名查询的次数作为将在签名查询中生成的群元素处理。C 与A 交互过程中群操作查询和签名查询的回答如下：

①令j为最大索引且zj≠0；

② 若j>qc+2，返回⊥退出；

③对于每一个i∈{1，2，…，j}，从(αi，Vi，-，-)列表中取αi计算z′=z1+z2d+z3α1+…+zjαjmodn；

④ 如果存在(z′，V′，-，-)在列表L中，挑战者C返回V′给A，否则，分为以下两种情形：

情形1 如果z2=0，任意选择V′，将(z′，V′，(z1，添加至列表L，将V′返回给A；

情形2 如果z2≠0，任意选择Z′∈{0，1}256，M′∈M3，计算h(Z′||M′))，然后将添加至列表L中，然后返回V′给A。

2）对于某些消息M的签名询问，挑战者C任意选取k∈Zn，计算α=h(d||M||k)；然后，进行群操作查询(α，0，…，0)获取V，计算x=f(V)，r=h(Z||M) +xmodn，s=(α-rd)/(1+d)modn，其中，Z为SM2签名算法中已知确定的信息；最后，挑战者C返回签名(r，s)作为A的询问应答。

假设哈希函数h是均匀分布且抗碰撞的，敌手A 通过上述询问，对于任意一个消息伪造出消息M*的签名(r*，s*)的概率是可忽略的，下面进行具体分析：

挑战者C 诚实地生成了公钥和签名，如果C 能够完美地回答群操作查询，那么说明C 几乎能够为敌手A 模拟一个完美的攻击环境。实际上，除了群操作查询的情形2 之外，所有的群元素句柄都是随机统一选择的。现在，假设情形2 中生成的V′=也是均匀分布的，事实上，Z′和M′是随机均匀选择的，且h是均匀哈希函数，则情形2 中f-1的输入是均匀分布的。根据f-1几乎可逆的事实，有V′是均匀分布的。另外，根据Schwartz-Zippel 引理［28］，在列表L中存在两个分量(z′，V′，-，-) 和(z′′，V′′，-，-)，其中，z′≠z″但V′≠V″，其概率是可忽略的，qG表示敌手A执行的群操作查询总数。

为了继续完成上述证明，只需要证明(r*，s*)在M*上有效签名的概率是可以忽略的。令α*=s*+(s*+r*)d，(r*，s*)是消息M*上有效的签名，当且仅当(α*，V*，-，-) 出现在列表L中，其中V*=f-1(r*-h(Z||M*))。若要证明(r*，s*)在M*上的有效签名概率是可以忽略不计的，就等价于证明(α*，V*，-，-)出现在表L中的概率是可忽略的。此处声明，V*∉{G，P}，否则，敌手A 可以通过使用s*≠0和s*+r*≠0确定地从(r*，s*)中计算d，此处与d对敌手A 完全隐藏的事实相矛盾。换句话说，V*只能在群操作查询或签名查询时创建。有以下两种情形：

情形1（V*在签名查询中被创建）：如果V*∈{V1，V2，…}，对于某个i设置V*=Vi，并设置(ri，si)为第i个签名查询消息Mi和辅助信息Zi的签名。换句话说，存在s*+(s*+r*)d=si+(si+ri)d，由于私钥d对敌手是完全隐藏的，所有只有当s*=si和s*+r*=si+ri同时保持一致才成立，这种情况才会发生且概率不可忽略。在这种情况下，(r*，s*)是M*上的有效签名，当且仅当方程h(Zi||Mi)=rf(V*)=h(Z||M*)保持成立。然而M*≠Mi，以上意味着敌手A 必须找到一个碰撞(Zi||Mi，Z||M*)，然而哈希函数h是抗碰撞的，所以以上情况只会以忽略不计的概率发生。

综上，在哈希函数h是抗碰撞的假设下，签名(r*，s*)是M*上有效签名的概率是可以忽略的，证毕。

5 性能分析

5.1 计算复杂度分析

下面针对抗替换攻击的SM2 签名算法的模乘、模逆及点积运算进行分析，一次模逆运算约等于算法执行9 次点积运算。本文采用[mc]、[mn]和[dj]分别表示模乘、模逆与点积运算，设一次模乘运算的数据规模为n，则一次模乘、模逆与点积运算的复杂度分别为O(n2log2n)、O(9n2)和O(n2)，其中[mn]=9[dj]。T1、T2分别表示SM2 签名算法与抗替换攻击的SM2 签名算法的总运算量，两种签名方案的运算量比较如表1所示。

表1 SM2签名算法与抗替换攻击的SM2签名算法运算量比较

表1 中T1=O[(2 log2n+13)n2]，T2=O[(2 log2n+13)n2]，抗替换攻击SM2 签名算法的计算复杂度等于SM2签名算法的计算复杂度。

5.2 算法执行效率分析

下面分别对SM2 签名算法和抗替换攻击的SM2 签名算法的效率进行测试，并对每个算法执行10 000 次，求其效率平均值。实验环境为Inter（R）Core（TM）惠普i5-7400CPU@3.00 GHz 处理器、Ubuntu16.0.4 LTS，64位操作系统，内存容量为6.00 GB的台式机，编译环境采用JetBrains PyCharm 2019.2.3版本，编译语言采用python 3.6.5编译程序。两种签名方案的密钥生成、签名及验证算法执行效率分别作对比如图1所示。

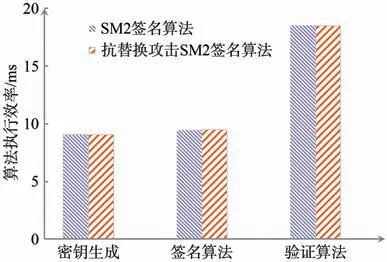
图1 两种签名算法执行效率对比图

根据图1 分析，SM2 签名方案与本文提出的抗替换攻击SM2 签名算法在密钥生成算法、验证算法执行效率相同。由于抗替换攻击SM2 签名方案在计算签名时引入了哈希函数计算辅助随机数耗时的原因，签名算法耗时比原始SM2 签名算法耗时长0.023 ms。综上，在签名长度相同的情况下，抗替换攻击的SM2 签名算法执行效率与原始SM2 签名算法的执行效率基本一致，而且还具备了抗替换攻击性。

6 结论

本文首先简要回顾了SM2 签名算法遭受的替换攻击；然后利用哈希函数将签名私钥、签名消息与其签名选择的随机数的哈希结果作为签名的随机组件，对原始的SM2 签名算法改进，构造了具备抗替换攻击的SM2 签名方案，并在一般群模型下证明了方案的安全性；最后，对提出的抗替换攻击SM2 算法与已有算法进行了效率测试，实验结果证明了提出的算法在计算复杂度与算法执行效率方面与已有算法基本一致。该签名算法的研究不仅有效的抵御了替换攻击带来的安全威胁，而且丰富了国产密码体系。