波纹管有限元建模方法

黄瀚林, 周仕明, 李道奎, 徐亮

(1. 国防科技大学 空天科学学院, 长沙 410000; 2. 空天任务智能规划与仿真湖南省重点实验室, 长沙 410000;3. 中国人民解放军77680部队, 西藏 山南 856000)

0 引 言

波纹管是用于补偿管路因温差或温度波动造成的轴向、横向和角位移的元件,其主要性能指标——轴向刚度、弯曲刚度等是衡量波纹管补偿能力的主要依据。对于单个波纹管性能指标的计算,国内外已制定了较为成熟的标准,其中美国的EJMA[1]标准以较高的计算精度而影响广泛,国内的GB/T 12777和JB/T 6169等标准均对EJMA标准进行引用。

波纹管在航空航天、石化、电力等领域运用越发广泛,对单个波纹管的分析已经很难满足复杂系统的需求。Ansys、Abaqus等有限元软件能将大量元件进行集成,对形成相互作用的系统进行整体分析,极大地提升分析效率。为确保分析结果正确,必须保证模型具有足够高的可信度[2],因此必须确保每个元件的建模方法合适。

一些学者结合自身研究目的,采用不同的有限元建模方法对波纹管进行研究。刘达列等[3]利用Ansys软件的Matrix27单元建立金属波纹管的简化有限元模型,与原波纹管模型进行等效,能极大地提高波纹管的建模效率和轴向刚度计算效率。刘卫鹏[4]通过建立金属波纹管有限元三维壳模型,对等参数金属波纹管在弯曲扭转联合工况下的性质进行研究,得到弯曲作用和扭转作用对等参数金属波纹管弹性性能的影响规律。刘江等[5]通过建立三层金属波纹管的有限元二维轴对称模型,分析波形结构参数中的波距、波高、层厚与轴向刚度的关系,得出轴向刚度随结构参数改变的变化趋势和规律。修筑等[6]将U形波纹管等效为梁模型,修正随厚度变化波纹管的轴向刚度计算公式,并建立波纹管三维壳模型和开展轴向刚度试验,验证修正公式的正确性。目前的研究大多采用一种有限元建模方法研究波纹管的性能参数,但并未有相关文献对波纹管有限元建模方法的适用性和适用范围进行区分。

为验证不同建模方法均适用于波纹管结构力学特性有限元分析,该文以波纹管为例,首先确定波纹管构型和工况环境,使用EJMA方法分别计算波纹管的轴向刚度、弯曲刚度和最大应力的理论值,再分别建立二维轴对称模型、三维壳模型和三维实体模型,用有限元方法求得波纹管的轴向刚度、弯曲刚度和最大应力值,最后将理论值与有限元数值进行对比,验证3种有限元建模方法的适用性。

1 波纹管刚度及应力理论计算

结合大型集成化系统工程背景,波纹管选型见表1。

表 1 波纹管结构参数

波纹管选材为D406A超高强度钢。其在293 K室温时弹性模量为210 GPa,屈服极限为1 620 MPa,在773 K高温时弹性模量为174 GPa,屈服极限为1 000 MPa,泊松比为0.3,密度为7.85×103kg/m3,热导率为434 W/(m·K),热膨胀系数为1.2×10-5K-1,延伸率大于8%,整体性能较好,在进行管路轴向补偿时能确保处于线弹性范围内。

采用EJMA标准计算公式对轴向刚度进行理论计算,该计算公式为:

(1)

式中:Kz为波纹管整体轴向刚度,N/mm;n为波纹管层数;E为设计温度下波纹管材料的弹性模量,MPa;Dm为波纹管平均直径,mm,Dm=Db+h;Db为波纹管内径,mm;h为波高,mm;t为波纹管成型后的单层壁厚,mm;N为波数;Cf为EJMA标准中波纹管的修正系数,在GB/T 12777标准中的表A.3和JB/T 6169标准中的表B.5均可快速查阅。

在EJMA标准计算的轴向刚度基础上,推导弯曲刚度的理论计算公式[7]为:

(2)

式中:Kw为波纹管整体弯曲刚度,N·mm;r0为波纹管的平均半径,mm。

在轴向位移作用下,波纹管的主要应力为轴向力引起的弯曲应力,EJMA标准计算公式为:

(3)

式中:σ6为轴向力引起的弯曲应力,MPa;e为计算单波总当量轴向位移,mm;Cd为EJMA标准中波纹管的修正系数,在GB/T 12777标准中的表A.2和JB/T 6169标准中的表B.6均可快速查阅。

图1为波纹管的部分结构参数,其中:Dw为波纹管外径;q为波距;r为波峰(波谷)曲率半径,单位均为mm;其余参数在上述公式中已作说明。设环境温度为293 K,将表1中的数值分别代入式(1)～(3),可求得波纹管的轴向刚度和弯曲刚度的理论值分别为29.72 N/mm和2 387.40 N·mm。当总的轴向压缩位移为2 mm、单波压缩轴向位移为0.125 mm时,由轴向力引起的弯曲应力为205.66 MPa。

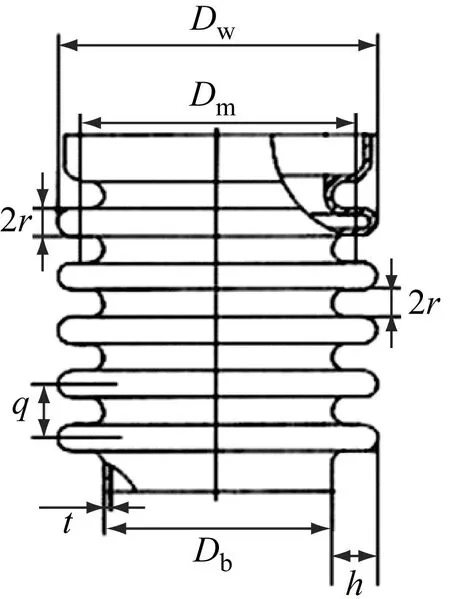
图1 波纹管的部分结构参数

2 有限元数值与理论值的对比

基于Abaqus有限元软件和表1的数值,分别建立波纹管的二维轴对称模型、三维壳模型和三维实体模型,采用相适应的网格划分方法,根据求解问题的不同分别设定相应边界条件,分别求解波纹管的轴向刚度、弯曲刚度和最大应力值,并与理论值对比。

2.1 3种有限元建模方法

建立波纹管二维轴对称模型。模型网格选用CAX4R单元,其具有模拟塑性、大变形、大应变、蠕变和应力强化等能力,当网格存在扭曲变形时,分析精度不会受到大的影响。

根据波纹管厚度,网格尺寸设为0.05 mm,网格总数为16 032个,均为四边形单元;波纹管外侧和内侧面设置自接触,接触面性质为法向作用硬接触,切向作用无摩擦和有限滑移;边界条件为一端固支,一端加载2 mm的轴向压缩位移,波纹管温度设为293 K。

通过有限元仿真得到轴向力-轴向位移曲线,计算波纹管的轴向刚度,并通过von MISES应力云图获得最大应力值。由于轴对称模型必须施加轴对称载荷,因此无法求解弯曲刚度。网格划分和边界条件设置见图2和3。

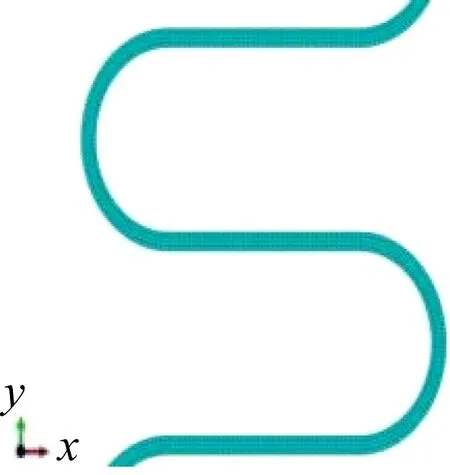
图2 二维轴对称模型有限元网格划分

图3 二维轴对称模型边界条件设置

建立波纹管三维壳模型,采用Standard/Liner中的4节点曲壳(S4R)单元进行网格划分,网格尺寸为0.4 mm,网格总数为100 230个,使用计算效率较高的减缩积分进行后续运算。该类型单元拥有4个节点,每个节点有6个自由度,包括3个平动自由度和3个转动自由度,此类单元可以较好地实现大变形和大应变的精准分析。利用Abaqus前处理模块经由旋转生成的波纹管三维壳模型,通过扫掠方式对变形体进行网格划分,可以获得规则的网格单元,有助于完成运算。

自接触设置与二维轴对称模型相同。边界条件首先设为一端固支,一端加载2 mm的轴向压缩位移,波纹管温度设为293 K。通过有限元仿真得到轴向力-轴向位移曲线,计算波纹管的轴向刚度,并通过von MISES应力云图获得最大应力值。后边界条件改为一端固支不变,另一端加载径向0.05 rad的转角位移,通过有限元仿真得到弯矩-转角曲线,计算波纹管的弯曲刚度。网格划分和边界条件设置见图4～6。

图4 三维壳模型有限元网格划分

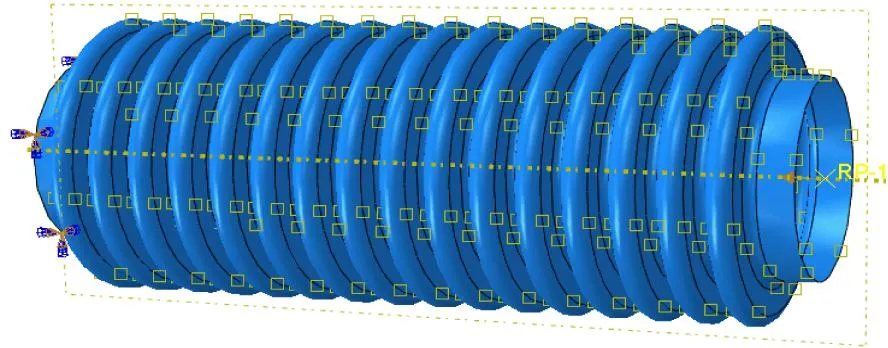
图5 三维壳模型边界条件设置(轴向压缩)

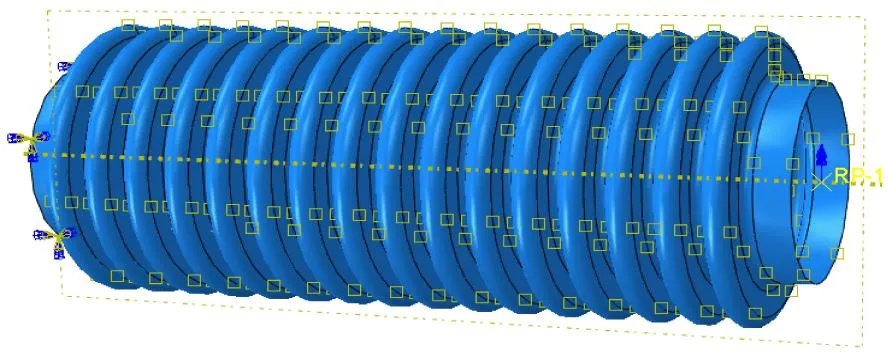
图6 三维壳模型边界条件设置(径向弯曲)

建立波纹管三维实体模型。实体模型的网格类型主要有四面体单元和六面体单元,六面体单元的精度高于四面体单元,绝大多数情况下推荐使用六面体单元进行有限元分析。但是,六面体单元形状过于规则,与实际工程结构的复杂外形不易贴合,在应用上有一定的局限性。四面体单元能适用于任何复杂外形的分析对象,简单四面体单元的形状函数满足完备性和相容性要求,可以用四面体单元分析三维变形问题。但是,四面体单元节点位移函数的阶数和项数较低,局部精度可能会受到影响[8]。

采用四面体单元作为波纹管的网格单元,网格尺寸为0.8 mm,网格总数为148 527个。为保证计算精度,采用Standard/Liner中的4节点实体(C3D10)单元进行网格划分,同样采用计算效率较高的减缩积分进行后续运算。边界条件设定同三维壳模型一致,网格划分和边界条件设置见图7～9。

图7 三维实体模型有限元网格划分

图8 三维实体模型边界条件设置(轴向压缩)

图9 三维实体模型边界条件设置(径向弯曲)

2.2 理论值与有限元数值对比

分别对比3种有限元模型和EJMA标准计算的轴向刚度和轴向压缩下的最大应力值,以及三维壳模型、三维实体模型和EJMA标准计算的弯曲刚度值的关系,结果见表2～4。

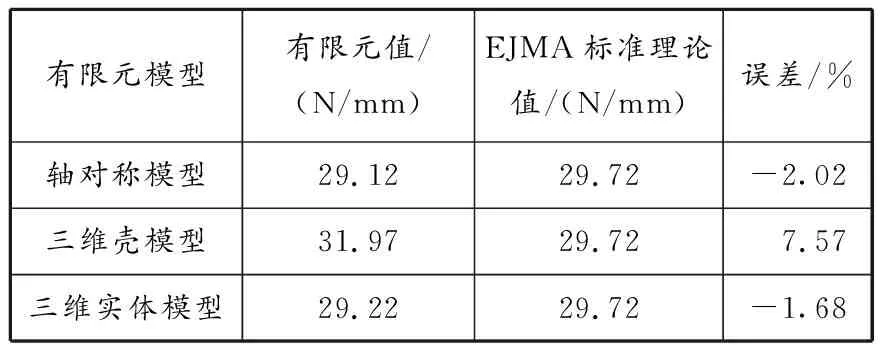
表 2 波纹管轴向刚度有限元数值与理论值对比

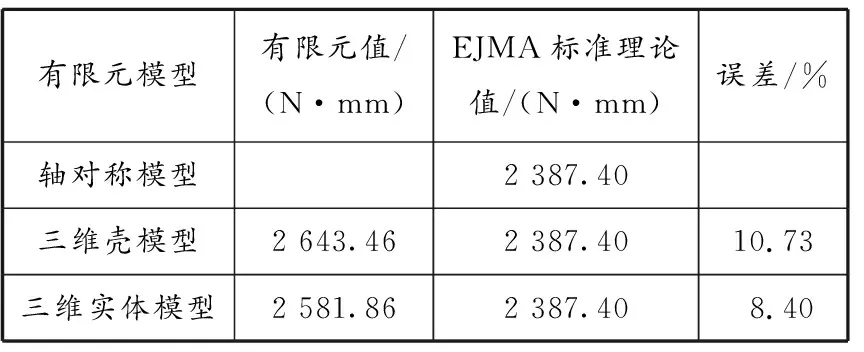
表 3 波纹管弯曲刚度有限元数值与理论值对比

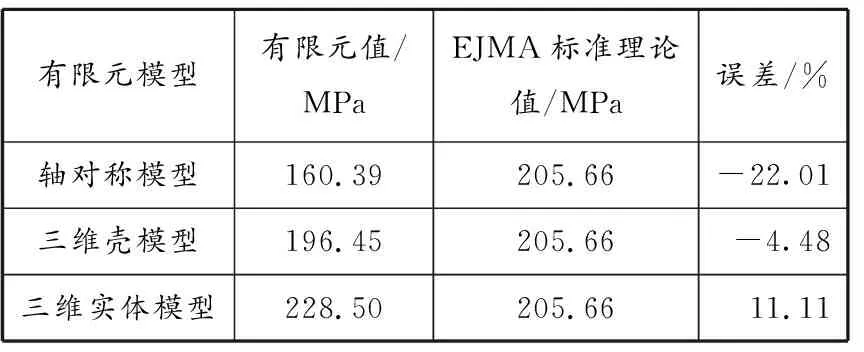
表 4 波纹管最大von MISES应力有限元数值与理论值对比

由表2～4可知,3种有限元模型计算轴向刚度有限元值与EJMA标准计算理论值最大误差为7.57%,三维壳模型和三维实体模型计算弯曲刚度有限元值与理论值最大误差为10.73%。3种有限元模型对波纹管轴向刚度和弯曲刚度的计算精度较高,其原因在于轴向刚度和弯曲刚度为波纹管的整体性能参数,在确保波纹管几何尺寸、材料参数和边界条件相同的前提下,能保证较高的计算精度。

在轴向压缩状态下,3种有限元模型的最大von MISES应力位置均位于波谷,而二维轴对称模型最大von MISES应力与EJMA标准计算理论值误差为-22.01%。出现较大误差的原因在于,二维轴对称模型是一种简化模型,无法完整计算波纹管的应力分布。

综上所述,由于模型结构以及网格类型的区别,不同模型计算数值存在一定误差,进一步改变3种有限元模型的网格尺寸,其误差仅有小幅变化,再次验证3种建模方法的合理性。从工程实际看,3种有限元模型均适用于波纹管的有限元分析。

2.3 3种有限元模型适用范围分析

虽然3种有限元模型均适用于波纹管有限元分析,但还应结合波纹管的结构、载荷、边界条件设置以及计算效率等合理选择建模方法,从而确保足够高的计算精度。

当波纹管不受力时为轴对称结构,且所受载荷为轴对称载荷,如单轴拉压、内外加压等,可以建立二维轴对称模型,并能提升计算效率。当波纹管不受力时为轴对称结构,且波纹管壁厚与平均半径之比<1/20时,优先建立三维壳模型,其既能加载轴对称载荷,又能加载非轴对称载荷,如弯曲、扭转等。当波纹管不受力时为非轴对称结构,如弯曲波纹管等,受限于部分CAE软件难以满足非轴对称波纹管三维壳模型的建模要求,此时可以通过CAD软件建模后导入CAE软件,生成三维实体模型进行有限元分析。

4 结 论

建立波纹管的二维轴对称模型、三维壳模型和三维实体模型,计算轴向刚度、弯曲刚度和轴向压缩状态下的最大应力值。通过对比3种有限元模型轴向刚度、弯曲刚度和最大应力有限元值与EJMA标准计算的理论值之间的关系,得出3种有限元模型均适用于波纹管结构力学特性有限元分析的结论,同时给出3种有限元模型的适用范围,为波纹管设计分析提供参考。