基于ABC-PSO的SHEPWM控制方法的优化
沈显庆, 张腾鹤, 徐梦泽, 王童正
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
三相逆变器是一种广泛运用于大功率场合的电力电子拓扑,但是因为功率器件的损耗的限制,导致输出电压、电流的低次谐波含量偏高。传统控制方式如SPWM、SVPWM,在其工作于低频时,控制效果较差,精度不高[1]。采用SHEPWM能够消除低频的特定次谐波,适用于在谐波要求高的场景。
SHEPWM技术的难点是,如何求解非线性方程组。传统的迭代方法,精度高,易于实现,但是对初值要求较为严格。代数方法,如结式理论、吴方法等,无需初值,但求解复杂,计算效率低[2-6]。魏远志给出神经网络和对称秩相结合的 SHEPWM 计算方法,解的精度高,但是会出现无解情况[7]。针对上述算法存在的问题,笔者采用改进的ABC-PSO算法求解SHEPWM的非线性方程组,使求出开关角的解易于收敛,求解精度高。
1 三相电压型逆变器
三相电压型逆变器如图1所示。三相逆变器SHEPWM相电压波形如图2所示。

图1 三相电压型逆变器拓扑

图2 三相逆变器SHEPWM相电压波形
根据Dirichlet定理将电压信号展开成傅里叶级数的形式:
(1)
(2)
(3)
电压的输出波形是关于π/2对称的,同时在[0,2π]的周期内以(π,0)对称,因此出现奇函数和奇函数谐波特性,满足如下公式[9-10]:
u(ωt)=-u(ωt+π),
(4)
u(ωt)=+u(π-ωt)。
(5)
由傅里叶分解所得的结果不再含有直流分量余弦分量和偶次正弦分量,其公式为
an=0,
(6)
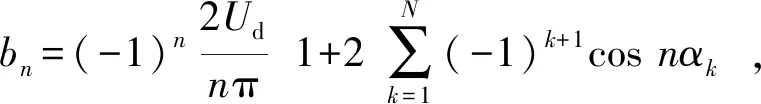
(7)
式中:n——谐波次数;
Ud——输入端电压;
α——开关角度。
输出电压的傅里叶频谱中只有sin的奇数次谐波,cos和sin项中的偶次谐波因对半波称性被消除,cos项的奇数次谐波因四分之一周期对称被消除。在三相系统中,由于矢量叠加为0,所以不存在3及其的整数倍的谐波[7-8]。
由式(7)可得,特定谐波消除的数学模型为
(8)
式中,bm——需要消除谐波的方程个数。
输出电压为
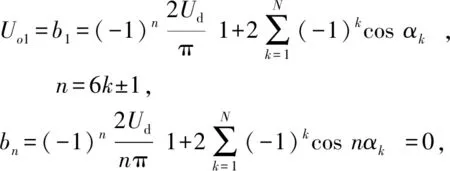
式中:αk——[0,π/2]k个开关角,0<α1<α2<…<αn<π/2;
n——开关角个数;
N——次数。
2 ABC-PSO算法的开关角求解
2.1 改进PSO算法原理
粒子群算法的主要模拟群体性的信息交流活动,每个个体具有学习能力,从而使种群进化。存在m维度空间,在这个空间内,每个粒子的位置Xi和速度Vi分别表示为
Xi=(xi1,xi2,…xiD),i=1,2…,N,
Vi=(vi1,vi2,…vin),i=1,2…,N。
粒子通过对目标进行优化,得出适应度函数。找到种群中适应度高的2个粒子,对其进行更新。
最优位置为
Pb=(pi1,pi2,…,piD),i=1,2,…,N。
最全局位置最优解为
Gb=(g1,g2,…,gD) 。
在粒子群中增加一种非线性惯性权重,以提高PSO的寻优特性。
式中:tmax——最大迭代次数;
t——当前迭代次数;
ωmax、ωmin——最大和最小权重值。
得到最优解后的速度和位置为
vij(t+1)=ωvij(t)+c1r1[pij-xij(t)]+
c2r2[pij-xij(t)],
xij(t+1)=xij(t)+vij(t+I),j=1,2,…,N,
式中:ω——惯性系数;
c1、c2——学习因子;
r1、r2——均匀分布在 0 至 1 间的随机数。
2.2 改进ABC算法原理
ABC人工蜂群算法是求解最优值问题的常用方法,蜂群分为3类:引领蜂、跟随蜂和侦查蜂。引领蜂开始对目标区域进行搜索,若搜索结果优于之前的结果,则用新位置代替旧位置,否则不变。在引领蜂搜索完成后,回到跳舞区将信息传给跟随蜂,跟随蜂对之前引领蜂的位置进行搜索,保留适应度更高的解。
计算每个蜜源的适应度值f为
式中,f(xi)——目标函数适应值,适应度按顺序排列。
取适应度高的为引领蜂,适应度低的为跟随蜂。
将人工蜂群算法的新蜜源搜索方式改为
vij=xij+rij(xij-xkj),
式中:Lk——当前算法的迭代次数;
k——随机数,k=1,2,…,N;
N——解的个数,j=1,2,…,N;
λ——设定步长值。
由此可见,算法初期,rij数值较大,算法后期rij较小,可加快算法的收敛速度[2]。
跟随蜂搜索蜜源中,根据适应度大小,以一定的概率跟随引领蜂进行采蜜。
式中:fi——解适应度;
pi——低i个引领蜂的概率。
在蜂群算法中,lim是某个解更新的次数,当此解在lim循环后多次未更新时,判定此解陷入局部最优,则该位置的引领蜂变为侦察蜂。假设放弃位置为xi,那么新产出的解的位置为
2.3 改进ABC-PSO算法
PSO算法模拟聚集性群体觅食行为,优化单极值函数问题,可以快速收敛到最优解[2]。但是对于多极值问题求解,可能会陷入局部最优,ABC算法模拟蜜蜂采蜜过程,通过探索更优的位置,从而实现数据优化[2]。
ABC-PSO算法同时运行拥有新蜜源搜索方式的ABC算法和改进的非惯性权重的PSO算法,运行结束后对种群适应度高的粒子进行交换,丰富了种群多样性,以此避免解陷入局部最优[3],求解精度更高。
Step1:设置参数,种群规模N,最大迭代次数L,学习因子c1、c2,惯性权重ω。
Step2:PSO算法种群标记为P1,ABC算法种群标记为P2,种群大小分别标记为n1、n2。
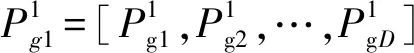
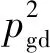
Step5:判断程序是否达到最大迭代次数或者要求的收敛精度,如果满足结束条件,则结束算法,否则继续迭代。
改进的ABC-PSO算法计算步骤,如图3所示。

图3 ABC-PSO流程
以7开关角为例,将ABC-PSO算法运用SHE-PWM方程组求解,消除5、7、11、13、17、19次谐波。
cosα1-cosα2+cosα3-cosα4+cosα5-
cosα6+cosα7-πm/4=ε1,
cos 5α1-cos 5α2+cos 5α3-cos 5α4+
cos 5α5-cos 5α6+cos 5α7=ε4,
cos 7α1-cos 7α2+cos 7α3-cos 7α4+
cos 7α5-cos 7α6+cos 7α7=ε3,
cos 11α1-cos 11α2+cos 11α3-cos 11α4+
cos 11α5-cos 11α6+cos 11α7=ε4,
cos 13α1-cos 13α2+cos 13α3-cos 13α4+
cos 13α5-cos 13α6+cos 13α7=ε5,
cos 17α1-cos 17α2+cos 17α3-cos 17α4+
cos 17α5-cos 17α6+cos 17α7=ε6,
cos 19α1-cos 19α2+cos 19α3-cos 19α4+
cos 19α5-cos 19α6+cos 19α7=ε7。
由此定义目标函数,
经过上述转换,多目标极值转化为单一目标极值[11],当函数值F取得最大值1时,ε1~ε7同时为0,所求出的开关角即为SHEPWM的解。
3 系统仿真
ABC-PSO算法具体参数为n1=50,ωmin=0.3,ωmax=0.7,c1=c2=1.2,tmax=L=200,lim=4,其他参数见表1。ABC算法蜜蜂总数为50,精英蜂和跟随蜂各25个,共享5个个体,种群个数的十分之一携带总体的全部信息。在Matlab2017b软件中运行ABC-PSO角度计算程序,计算N=7时的开关角数据。ABC-PSO算法的适应度曲线如图4所示。
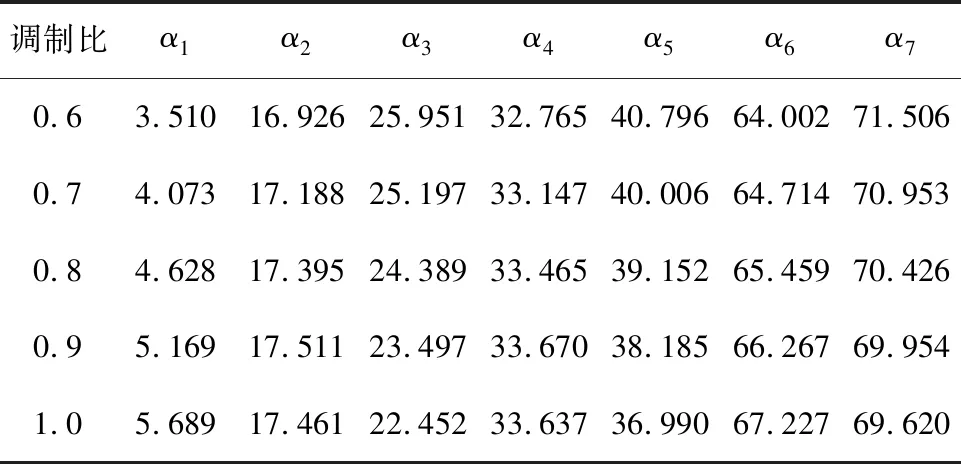
表1 ABC-PSO开关角解集
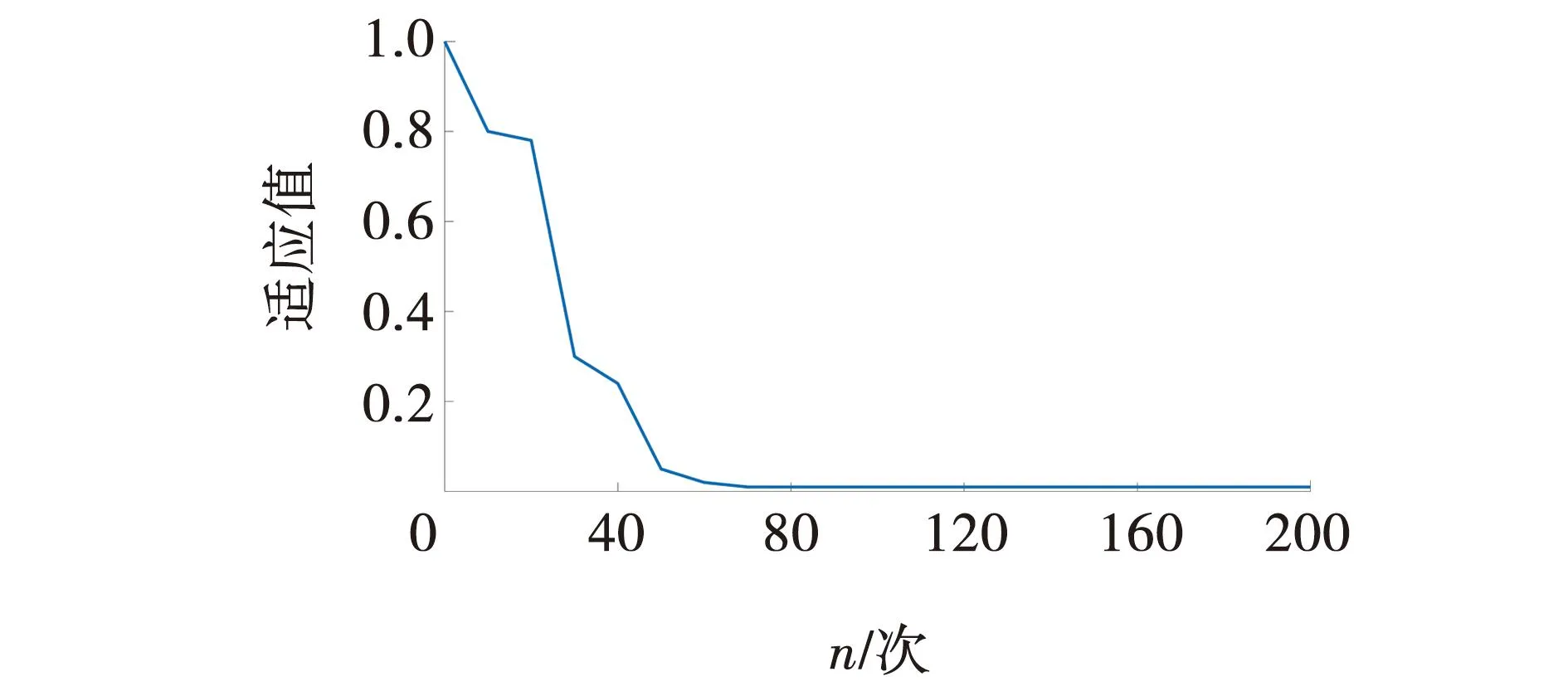
图4 ABC-PSO适应度曲线
由图4可以看出,改进ABC-PSO算法能在短时间内计算出最优解,且不容易陷入局部最优。为了验证算法求解SHEPWM非线性方程组的有效性,在Matlab/Simulink环境下搭建三相逆变器仿真系统模型进行仿真,输入电压为400 V,输出频率为50 Hz,负载类型为阻感负载,R=10 Ω,L=10 mH。表2~4分别为m=0.6、m=0.8、m=1时牛顿迭代法与ABC-PSO算法电流谐波对比数据如图5~7所示。

表2 m=0.6牛顿迭代法与ABC-PSO算法电流谐波分布

图5 m=0.6电压谐波分布
由表2对比可知,在m=0.6的条件下,牛顿迭代法的电流谐波含量为14.14%,ABC-PSO算法电流谐波含量为13.31%,同调制度下电流谐波降低0.83%。
当m=0.6时,线电压谐波分布,如图5所示。可以明显看出ABC-PSO算法的线电压THD相比于牛顿迭代法的线电压THD低12.9%,23次谐波降低4%。由表3对比可知,在m=0.8的条件下,牛顿迭代法的电流谐波含量为12.52%,ABC-PSO算法电流谐波含量为11.76%,同调制度下电流谐波降低0.76%。

表3 m=0.8牛顿迭代法与ABC-PSO算法电流谐波分布
当m=0.8时,线电压谐波分布,如图6所示,可以明显看出,ABC-PSO压的THD相比于牛顿迭代法电压的THD低11.87%,23次谐波降低13%。

图6 m=0.8时电压谐波分布
m=1.0时线电压谐波分布如图7所示。由图7可见,ABC-PSO算法的电压THD相比于牛顿迭代法的电压THD低5.61%,23次谐降低到5%。

图7 m=1.0电压谐波分布
由表4对比可知,在m=1.0的条件下,牛顿迭代法的电流谐波含量为9.52%,ABC-PSO电流谐波含量为8.75%,同调制度下电流谐波降0.77%。
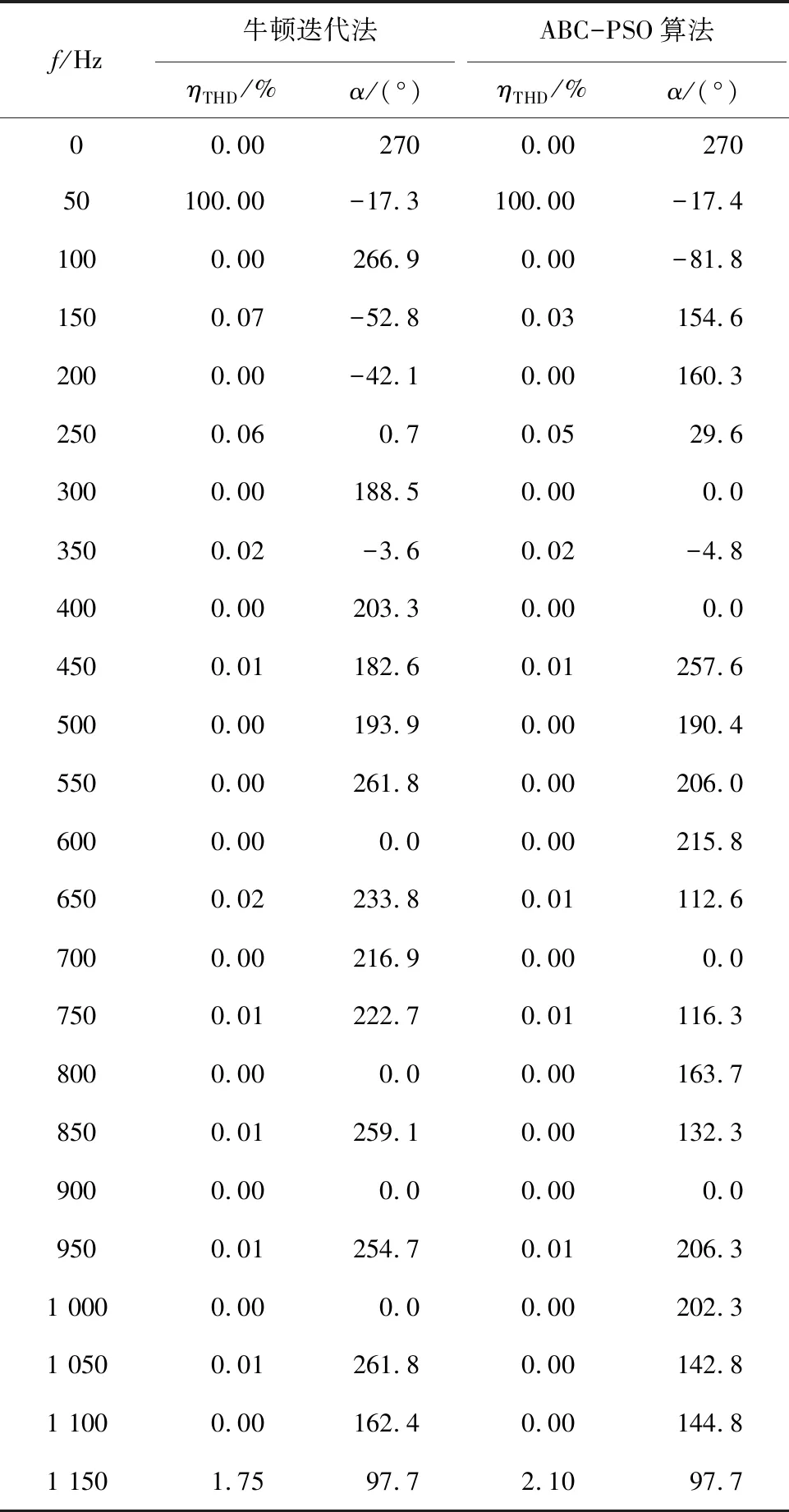
表4 m=1.0牛顿迭代法与ABC-PSO算法电流谐波分布
4 结 论
(1)运用ABC-PSO对三相逆变器的SHEPWM的非线性方程求解,给出了调制比在0.6~1.0的开关角解集。将改进的PSO与ABC算法相结合能够获得更加精确的开关角度,提高SHEPWM的谐波消除特性,克服了传统算法对初值要求高,收敛速度慢等问题。
(2)通过与牛顿迭代法相对比,相同调制度下ABC-PSO算法具有更低的电压、电流谐波含量。仿真结果证明采用ABC-PSO算法求解SHEPWM具有更高的准确性,为求解SHEPWM方程组提供了新的求解方式。

