缺陷参数对含双腐蚀储罐剩余承载力的影响

周利剑, 董守业, 于新杰

(东北石油大学 土木建筑工程学院, 黑龙江 大庆 163318)

0 引 言

疫情防控进入新阶段,以我国为代表的国家及地区经济恢复势态向好,对油气等能源需求增长强劲[1]。储罐作为石油储存的核心设备,其安全性已成为使用过程中首要考虑的问题,如果发生泄漏或者爆炸事故,将会造成严重的经济损失甚至威胁生命安全[2]。腐蚀问题是影响储罐安全运行的关键因素之一。腐蚀缺陷的存在导致储罐在局部出现应力集中现象,进而使壁厚局部减薄,这极大地削弱储罐的强度[4-7]。长庆油田1 000 m3以上的储罐超半数出现了不同程度的腐蚀损失,每年因腐蚀产生的维护费用高达数千万元[3],因此,有必要开展符合油田现状的含腐蚀储罐剩余承载力的研究。

国外学者Jae等[8]对存在腐蚀缺陷的原油储罐进行实验,得出储罐强度的变化规律。Masahiro[9]分析了不同使用年限储罐各个部位的剩余强度,得出罐顶部位的强度退化最为严重。Mostafa等[10]应用Taguchi分析方法,确定了含腐蚀缺陷储罐的应力分布情况。梁洪爽[11]针对沿海地区原油罐的主要腐蚀形式,对罐壁及罐底表面腐蚀与防护技术进行了总结,并且阐述了储罐涂层防护、牺牲阳极阴极保护法和外加电流阴极保护法三种防护技术的特点和应用现状。国内一些学者总结了各地储油罐腐蚀的主要原因,并提出相应防护措施[12-18]。也有少部分学者利用有限元的方法对含腐蚀缺陷储油罐进行数值仿真模拟。吴媚[19]以绥中36-1终端储罐为例,建立了含腐蚀缺陷的储罐有限元模型,着重研究了腐蚀深度为1.5与3 mm工况下罐壁的等效应力变化情况。刘雪云[20]对储罐检测数据进行统计分析,建立了储油罐两种腐蚀类型的分布模型,并阐述了凹坑对储罐强度的影响规律。

鉴于原油储罐实际的腐蚀情况更多的是双腐蚀或者是腐蚀群,笔者在众多学者的研究基础上,根据储罐自身特点和腐蚀机理,借助有限元软件探究不同腐蚀参数下含双腐蚀缺陷原油储罐剩余承载力的变化规律,并对不同腐蚀深度下储罐剩余承载力结果进行拟合,为含腐蚀储罐的安全评估以及后续维护检修提供理论依据。

1 模型的建立

1.1 储罐几何特征和力学性能

利用ABAQUS有限元软件建立了1 000 m3储罐模型,储罐的几何参数和物理性能参数如表1所示。罐壁的材料采用Q345R钢材,密度为7 850 kg/m3。罐底边缘板厚度为2 mm,材料同样采用Q345R钢材。建模时考虑到储罐结构几何尺寸和荷载的对称性,选取外腐蚀缺陷储罐的1/4建立有限元模型,模型采用六面体网格划分。为了精确地模拟腐蚀缺陷周围的应力分布,对含腐蚀缺陷的区域进行网格加密处理,未腐蚀区域进行粗略划分。

表1 储罐模型基本参数

1.2 缺陷选取

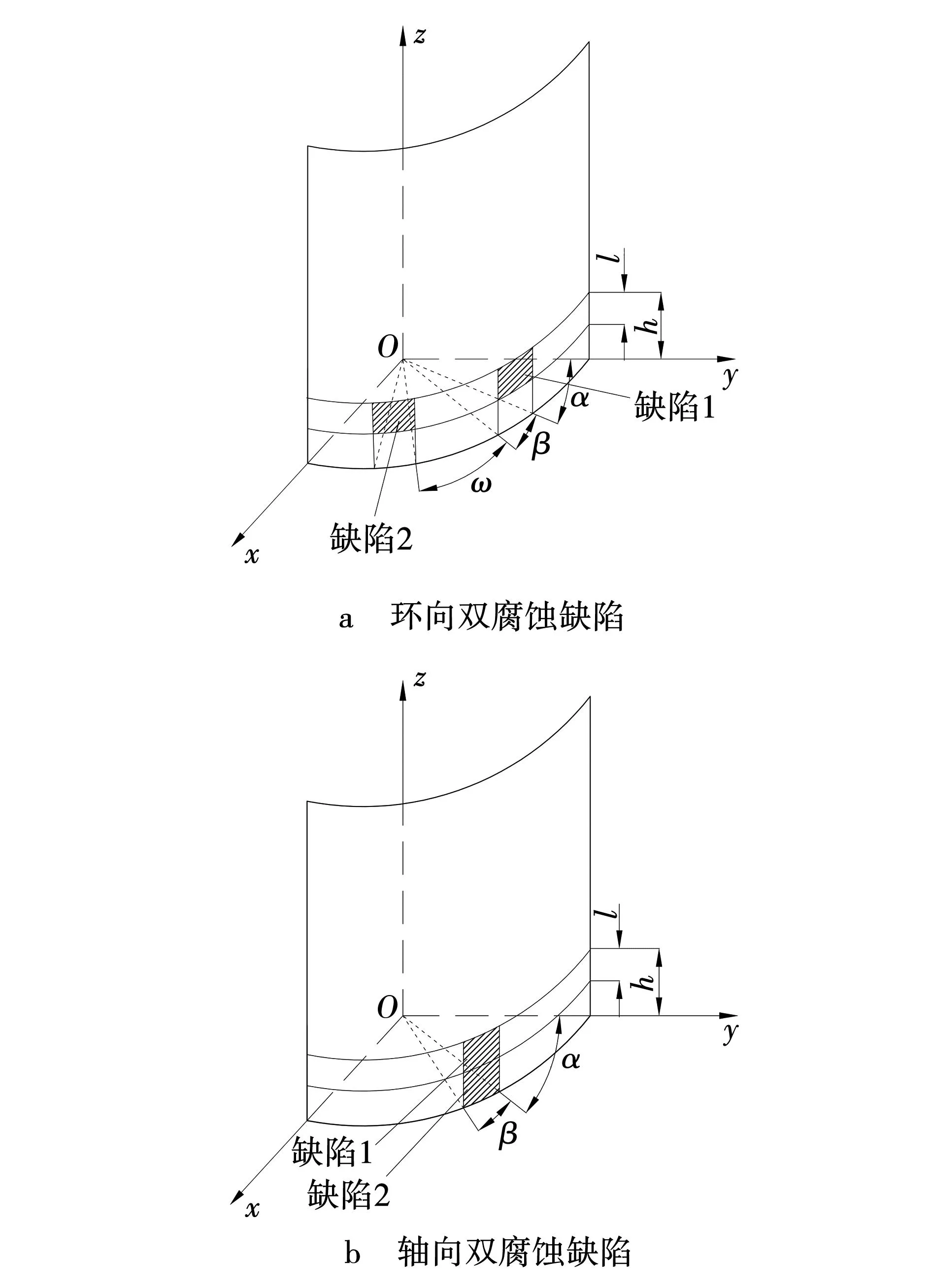
图1 罐壁腐蚀缺陷示意

1.3 边界条件与荷载的施加

考虑到结构和荷载的对称性,对储罐有限元模型横截面、纵向剖开面分别施加轴向约束和对称约束,罐底施加完全固定的约束。忽略风荷载、地震荷载等的影响,只考虑储罐重力和储液静压力,对整个模型施加z轴负方向重力加速度,储液压力p为

p=ρgh,

(1)

式中:p——储液静压力,Pa;

ρ——储液密度,取860 kg/m3;

g——重力加速度,取9.8 m/s2;

h——储液高度,m。

2 Von Mises应力与剩余承载力

根据API 590规范[23],水压试验时材料的许用应力[σ]一般取 min(3σs/4,3σb/7),其中,σs、σb分别代表材料的屈服强度与抗拉强度,计算得[σ]为219 MPa。Von Mises应力σv是根据第四强度理论得到的当量应力,综合考虑了第一、第二、第三主应力,通过应力等值线可以清晰地表示材料内部应力的分布情况。当Von Mises应力在许用范围以内时,结构满足要求,可以安全运行。当应力值超出许用应力时,储罐发生失效,应该停止使用或者采取合适的方法进行补救。在三维主应力空间,Von Mises应力σv条件表达式为

(2)

式中:σ1——x方向上的应力,MPa;

σ2——y方向上的应力,MPa;

σ3——z方向上的应力,MPa。

结合结构功能函数[Z=g(R,S)=R-S],其中,R为结构抗力,S为作用效应,取许用应力[σ]与最大Von -Mises应力σvmax的差值为剩余承载力σr,即:

σr=[σ]-σvmax。

(3)

3 储罐剩余承载力分析

首先,分别考察双腐蚀缺陷储罐应力云图分布特点,其次,探究储罐在不同腐蚀缺陷参数下最大Von Mises应力和剩余承载力的变化规律。

3.1 环向腐蚀间距

固定缺陷1的位置不变(α=45°,h=1 m,β=1°)腐蚀长度取0.1 m,腐蚀深度δ取3 mm,缺陷2在储罐圆周上移动,分别取不同的位置。ω表示两缺陷的环向间距。ω分别取为0.1°、0.2°、0.5°、1°、5°、10°。在腐蚀长度、宽度、深度都不改变的情况下,通过改变环向腐蚀间距来探究储罐最大Von Mises应力和剩余承载力的变化规律,从而得出环向腐蚀间距对储罐剩余承载力的影响。部分模型应力云图见图2,储罐的应力状态变化见表2。

图2 环向腐蚀间距下储罐应力云图

表2 腐蚀环向间距变化时储罐的应力

由图2可见,最大Von Mises应力出现在各腐蚀缺陷的中心处。接近腐蚀区域的位置,应力较大,远离腐蚀缺陷区域,应力值相对较小并且分布均匀。这是由于双腐蚀缺陷造成储罐几何形状不连续进而产生不连续应力,使腐蚀区域的应力值会明显大于未腐蚀区域,承载能力会显著下降,容易发生强度失效。环向腐蚀之间的区域应力值较小,没有出现应力集中现象,说明环向腐蚀间的相互作用不明显。

由表2可见,当环向间距小于2°时,随着间距的逐渐增大,储罐的最大Von Mises应力逐渐增加,剩余承载力随之不断减小,即环向间距与剩余承载力的大小成反比。腐蚀缺陷的环向距离大于2°时剩余承载力基本维持不变,此时罐壁的承载能力依旧有较大的富余,工程上可以忽略环向双腐蚀的影响。

3.2 轴向双腐蚀长度

保持腐蚀缺陷2的位置不变(α=45°,β=1°)缺陷厚度δ取3 mm,长度取为0.1 m。缺陷1在缺陷2的上方,腐蚀长度l在0.1 ～0.15 m范围内取值。两缺陷的轴向距离d分别取0.1ls(17.3 mm)、0.2ls(34.6 mm)、0.5ls(86.6 mm)、ls(173.2 mm)、2ls(346.4 mm)。根据以上参数,建立储罐有限元模型,分析在腐蚀宽度、腐蚀深度一定时,不同腐蚀长度对储罐整体剩余承载力的影响情况。选取部分模型应力云图见图3。

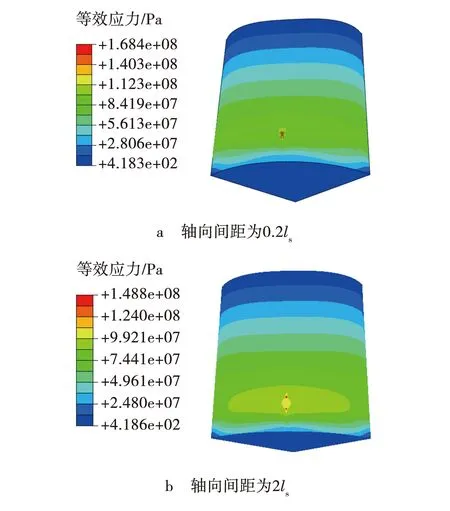
图3 轴向腐蚀下储罐应力云图

由图3可见,当轴向腐蚀间距较小时,最大Von Mises应力分布在腐蚀缺陷中心以及周围区域。缺陷中心以及两缺陷之间都产生了应力集中现象,考虑到此时两缺陷之间存在相互作用。当轴向腐蚀间距为2ls时,最大Von Mises应力主要分布在缺陷中心处,缺陷之间的区域应力值相对较小,此时两缺陷间的相互作用减弱或者消失。未腐蚀区域的应力小于腐蚀区域应力。

图4描述了不同轴向腐蚀间距下储罐的剩余承载力变化曲线。从图4中可以看出,轴向腐蚀间距与罐壁的剩余承载力之间呈现明显的对数关系。当双腐蚀间距在0.1ls～ls(17.3～173.2 mm)变化时,剩余承载力会随着轴向间距的增加而稳步上升,当轴向间距大于ls时,剩余承载力的变化趋于平缓。这表明两腐蚀缺陷之间的相互作用在轴向距离为ls时开始缓慢消失。

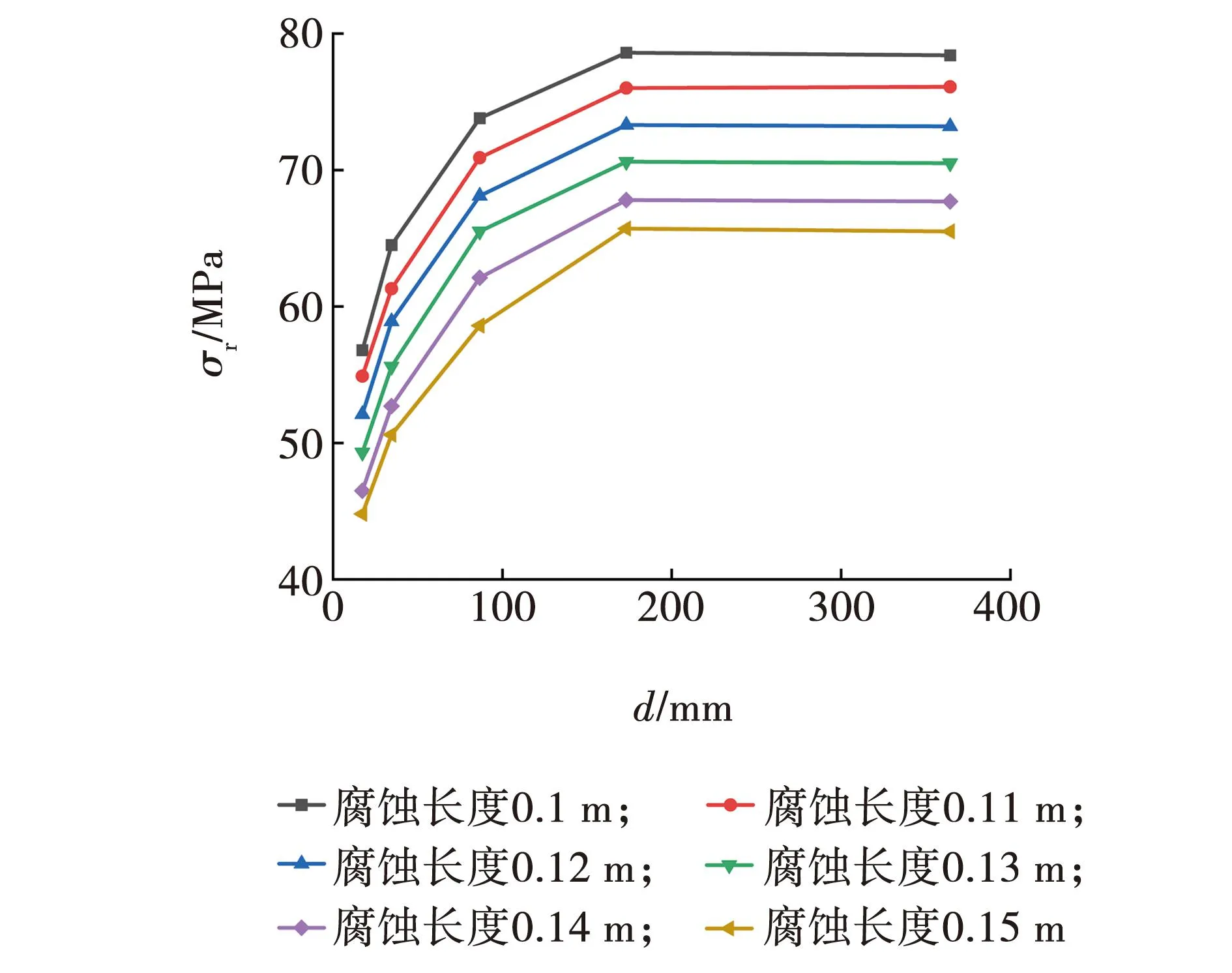
图4 轴向间距对剩余承载力的影响

图5为不同腐蚀长度对罐壁剩余承载力的影响。从图5中可以看出,随着腐蚀长度的增加,储罐的剩余承载力在逐渐减小,腐蚀长度与储罐的剩余承载力之间呈线性关系。5组腐蚀间距下,腐蚀长度在0.10 ～0.15 m变化时,剩余承载力的波动范围在8.2 ～15.2 MPa之间。说明腐蚀长度的改变对罐壁的剩余承载力状态有一定的影响,在役储罐若出现长度较大的腐蚀缺陷,其剩余承载力状态会有较大波动,应当及时采取措施防止底部罐壁腐蚀长度过大导致储罐发生破坏。

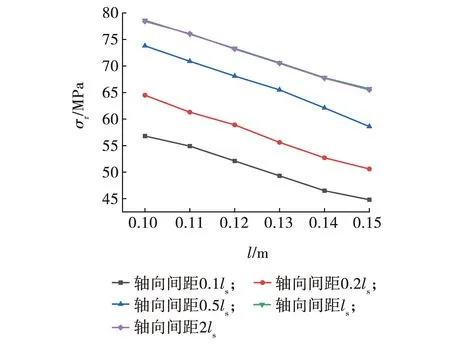
图5 腐蚀长度对剩余承载力的影响

3.3 轴向双腐蚀深度

同样,保持腐蚀缺陷2的位置不变(α=45°,β=1°),长度取0.1 m。缺陷1在缺陷2的上方,长度为0.1 m。两腐蚀缺陷腐蚀深度δ分别取0.2T(1 mm)、0.4T(2 mm)、0.6T(3 mm)、0.8T(4 mm)。轴向距离d分别取0.1ls(17.3 mm) 、0.2ls(34.6mm)、0.5ls(86.6 mm)、ls(173.2 mm)、2ls(346.4 mm)。在腐蚀宽度和腐蚀长度不变的情况下分析不同深度的腐蚀缺陷对储罐剩余承载力的影响。

图6表示不同深度下腐蚀间距与剩余承载力的关系曲线,可以看出,不同腐蚀深度下轴向间距与剩余承载力同样呈现对数关系。当轴向间距大于ls(173.2 mm)时,剩余承载力的变化趋于平缓。与图4的差别之处在于不同腐蚀深度之间罐壁的剩余承载力变化幅度更加明显。

图6 轴向间距对剩余承载力的影响

图7表示不同腐蚀深度下罐壁剩余承载力的变化。由图7可知,随着腐蚀深度的增加,储罐的剩余承载力逐渐减小,腐蚀深度与储罐的剩余承载力之间呈现非线性关系。腐蚀深度较小时轴向间距对剩余承载力的影响较弱,随着深度的增加,不同轴向间距之间的剩余承载力变化幅度开始逐渐变大,由开始的4.5 MPa变化至43.9 MPa。当腐蚀深度扩展到3 mm时,承载力曲线急剧下降,深度达到4 mm,特别是在轴向间距为0.1ls时,储罐的承载力剩余值仅为16 MPa,面临失效的危险。综上可知,腐蚀深度的改变对罐壁的剩余承载力状态影响极大,在对含有腐蚀缺陷的储罐进行防护时,要重点考虑腐蚀深度对罐壁剩余承载能力的影响,并且要及时采取措施抑制腐蚀深度的扩展。

图7 腐蚀深度对剩余承载力的影响

4 非线性拟合

由于腐蚀深度对储罐的承载力状态有显著影响,并且当两腐蚀缺陷之间间隔较小时储罐的剩余承载能力最弱,在外荷载作用下很可能会发生强度失效。因此,文中对间距为0.1ls时的腐蚀深度进行细化,剩余承载力计算结果如表3所示。

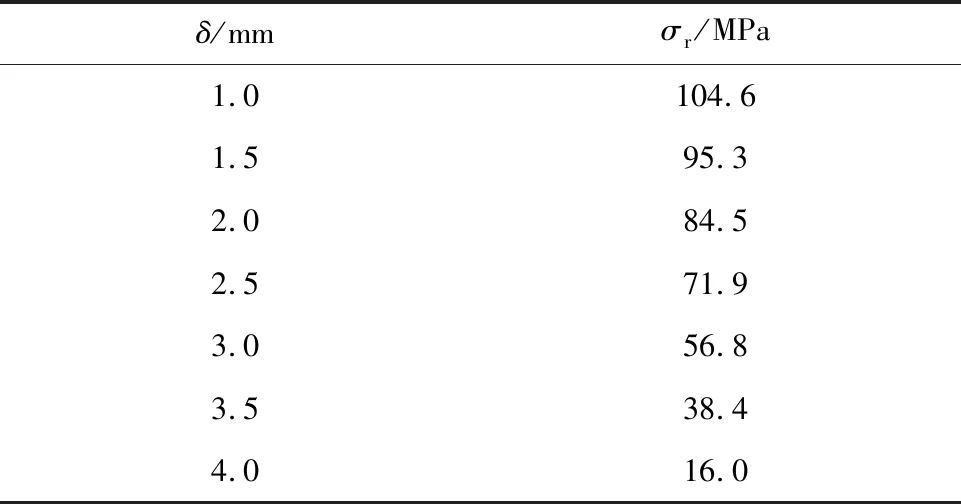
表3 不同腐蚀深度下剩余承载力计算结果

根据表3中的数据绘制剩余承载力与腐蚀深度关系点,并进行多项式拟合(图8),得到剩余承载力公式为

图8 剩余承载力计算结果及拟合曲线

σr=112.39-5.166 7δ2-3.259 2δ,

(4)

式中:δ——腐蚀缺陷深度;

σr——剩余承载力。

拟合公式的相关系数为0.980,说明拟合曲线有效。通过对拟合曲线分析发现,储罐的腐蚀深度同剩余承载力之间呈非线性关系,剩余承载力随着腐蚀深度的增加而逐渐减小。通过回归方程可以粗略计算出不同腐蚀深度下储罐的剩余承载力,为初步评估采油厂储罐安全性提供参考。

5 结 论

(1)含腐蚀缺陷的原油储罐最大等效应力出现在缺陷中心区域,在此区域内储罐的应力急剧增加,腐蚀坑处出现应力集中现象,远离双腐蚀缺陷区域,应力基本维持不变。

(2)环向间距小于2°时,储罐剩余承载力的大小与腐蚀间距成正比;环向间距大于2°时,储罐的剩余承载能力基本维持不变。腐蚀缺陷的轴向间距与剩余承载力之间呈现明显的对数函数关系,轴向间距较小时,缺陷间会产生交互作用,使储罐的承载能力降低,当轴向间距大于时,缺陷间的相互作用逐渐消失。

(3)腐蚀长度与储罐的剩余承载力之间呈线性关系,当腐蚀长度在0.10 ～0.15 m变化时,剩余承载力的波动范围在8.2 ～15.2 MPa之间。腐蚀深度与储罐的剩余承载力之间表现为非线性关系,当深度达到3 mm时,承载力曲线开始大幅下降,需要及时采取相应措施抑制腐蚀深度的扩展。

(4)通过拟合分析,得到用于含双腐蚀缺陷储罐腐蚀深度与剩余承载力的计算公式,为初期储罐的维护和检修提供参考。