霍尔辛赫3501 回风巷塑性区演化规律与支护研究

李建功

（山西霍尔辛赫煤业有限责任公司，山西 长治 046000）

0 引言

近年来，伴随科学技术的进步，我国煤炭资源需求日益增加，安全、高效生产成为煤矿生产的主要目标之一。多数矿井采用双巷布置方式代替原来所采用的布置方式，以此缓解矿井运输、通风、工作面接替紧张等问题，但保留上工作面运输巷在本工作面回采时会同时受到超前支撑压力以及上工作面采空区的侧向支撑压力叠加影响，造成留巷矿压显现剧烈且维护时间较长，故保证留巷服务期内留巷支护稳定性尤为关键。我国众多学者针对双巷布置的巷道稳定性问题进行了大量研究。在留巷应力分布方面，王书文等[1]通过连续6 个月现场监测，获取了工作面回采过程中采空区侧向支承压力演化规律；康红普[2]通过分析现场采动应力监测数据，论述了煤矿地应力场分布特征、规律以及回采工作面超前支承压力分布范围、峰值大小。在留巷变形破坏机理方面，马念杰等[3-5]提出了巷道非均匀应力场条件下蝶形塑性区理论，解释了巷道非均匀变形机理，得到了非均匀应力场下巷道围岩塑性区半径计算公式；刘洪涛等[6]以实际工程为背景，通过理论分析和数值模拟，研究获得留巷主应力的变化规律、塑性区扩展特征，解释了发生非对称变形的原因；张天等[7]通过现场调研结合数值模拟和工业性实验研究了多次采动巷道围岩变形及塑性区演化规律。在巷道围岩控制方面，王宇等[8]结合工程实际，建立工作面侧向采动应力模型，求得侧向塑性区破坏深度和采动应力的分布规律，提出采用非对称锚网索密集支护方案；赵志强[9]研究了大变形回采巷道围岩变形破坏机理，提出控制围岩塑性区扩展的原理，开发可接长锚杆-普通锚杆的协同支护技术；贾后省等[10]通过对受多次采动影响巷道的冒顶及大变形问题进行研究，发现通过增强支护强度无法有效控制顶板下沉，采用高延伸率、大锚固范围支护材料可以有效防止巷道冒顶。

本文以霍尔辛赫煤矿3501 回风顺槽为工程背景，通过数值模拟和理论分析研究受重复采动影响下的留巷塑性区演化规律，依据塑性区分布规律，同时结合现场实际情况对留巷支护参数提出优化方案。

1 工程概况

山西霍尔辛赫煤矿3501 工作面位于山西组3 号层五盘区，工作面东侧为中部风井，南侧为五盘区大巷，西侧布置为3502 工作面，工作面平面布置图如1所示。3501 工作面开采3 号煤层，煤层厚5.2～6.0 m，平均厚5.6 m，工作面外切眼长120 m，对接后切眼长246 m，工作面底板为泥岩，属于软弱岩层。工作面采用三巷布置，两进一回，分别为3501 运输顺槽、3501进风顺槽和3501 回风顺槽。

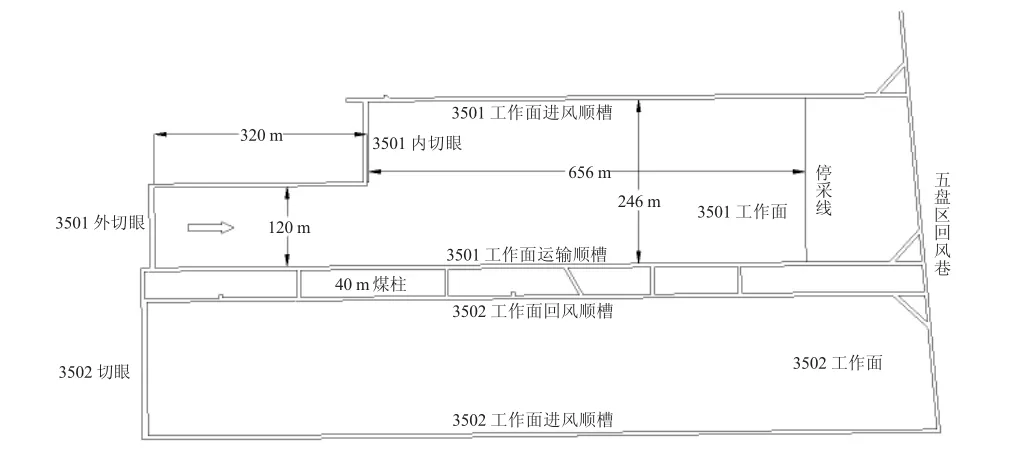
图1 工作面平面布置图

2 数值模拟分析

采用FLAC3D数值模拟软件对采用双巷布置时留巷受采动应力影响下的塑性区分布进行模拟，结合钻孔柱状图和岩石力学参数建立采场，模型大小为603 m×500 m×65 m，对留巷所在区域网格进行局部加密，网格细划为0.5 m，其余网格划分为2～5 m 不等，限制模型前、后、左、右、下等五个模型表面的位移，模型设置为Mohr-Coulomb 准则，模型如图2 所示。

图2 数值模拟模型示意图

分别模拟3501 工作面回采不同推进距离以及3502 工作面回采不同推进距离时留巷的塑性区分布，选取模型3501 工作面回风顺槽250 m 处作为观察面，提取两工作面不同推进距离时的留巷围岩塑性区分布情况，研究留巷受不同采动影响下的塑性区分布演化规律，两个工作面不同采动影响下的塑性区分布如图3、图4 所示。

图3 3501 工作面推进不同距离时留巷塑性区分布

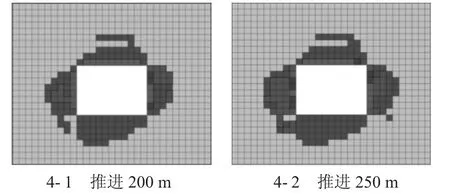
图4 3502 工作面推进不同距离时留巷塑性区分布

3501 工作面回采时，3501 回风顺槽受一次采动影响，随着工作面不断推进，留巷围岩塑性区逐渐向围岩深部扩展，塑性区呈现出非对称变形特征，推进300 m 时巷道底板塑性区最大值偏向于巷道副帮方向，而巷道顶板塑性区最大深度处偏向于巷道正帮，呈现为非对称塑性区，巷道整体塑性区往副帮与底板夹角和正帮与顶板夹角两处呈对角发展。工作面回采推进破坏了留巷周围应力分布的对称性，造成了巷道主应力的偏转，形成塑性区的非对称分布。

3501 工作面回采结束后，经过留巷稳定阶段，3501 回风顺槽塑性区没有发生新的变化。当接续工作面3502 工作面开始回采时，工作面前方形成的超前采动应力打破了受一次采动影响已经形成的非对称塑性变形巷道的稳定性，使其已经形成的塑性区发生进一步扩展。从模拟结果可以看出，随着3502 工作面不断推进，留巷塑性区在原基础上扩大了破坏程度，呈现出了更为明显的不均匀性和非对称性；留巷底板塑性区与副帮塑性区形成联通，进一步向夹角处发展，从形态上形成旋转的“蝶形”塑性区。

3 采动留巷塑性区演化规律

巷道围岩一般具有非均质的各向异性，因此想要精确计算巷道的围岩应力具有一定难度。因此一般将其简化为平面应变问题来求解，根据文献[9]中巷道围岩应力计算公式（1），推导出双向不等压巷道围岩塑性边界方程，即公式（2）。

式中：σθ、σr、τr，θ分别代表任意一点的环向应力、径向应力和剪应力，MPa；λ 为侧压系数；γH 为巷道竖向载荷，MPa；R0为圆形巷道半径；r、θ 为任一点的极坐标。

根据上述公式可以求得不同条件下巷道围岩塑性区的不同形态特征，分析可知巷道在不同侧压系数下围岩塑性区形貌会出现较大差异，巷道侧压系数小于0.5 时，巷道塑性区出现“蝶形”，这种形态的塑性区由于其最大尺寸与最小尺寸相差较大，不利于巷道围岩的稳定。

上文中数值模拟结果中塑性区出现的非对称形态可以看成是不规则的“蝶形”塑性区，“蝶形”塑性区的旋转造成蝶叶处于顶板与两帮夹角处，巷道围岩塑性区的最大深度出现在巷道肩部偏向帮部位置，在该处容易出现巷道冒顶及大面积片帮，因此在支护设计中应重点关注。

4 支护参数优化设计

3501 回风顺槽原支护顶板采用“锚杆+锚索+金属网”的联合支护形式，顶锚杆选用直径为22 mm、长2 400 mm 的左旋螺纹钢锚杆，间排距为1 100 mm×1 100 mm，锚索直径为22 mm、长度为7 300 mm，锚索间距为1 600 mm，每隔2 200 mm 打一排；巷道两帮采用“锚杆+钢护板+金属网”的支护方式，锚杆间排距为1 000 mm×1 100 mm，帮部金属网为菱形网，网片规格3 500 mm×1 200 mm，网孔规格50 mm×50 mm，原支护平面及断面图如图5 所示。

图5 3501 回风顺槽原支护平面及断面图（单位：mm）

根据上文数值模拟留巷塑性区分布情况，留巷在受不同采动影响时塑性区分布呈现不规则形状；留巷在受二次采动期间，巷道围岩塑性区在一次采动基础上发生恶性扩展，且巷道非对称破坏现象加剧，在此基础上原支护采用对称支护，针对留巷出现的非对称变形，原支护无法完全起到锚固作用，不能有效控制巷道因为应力偏转而出现的大面积冒顶和变形。

针对上述问题，结合数值模拟塑性区分布以及留巷塑性区演化规律，提出留巷的支护优化设计，新支护平面及断面图如图6 所示。

图6 3501 回风顺槽新支护平面及断面图（单位：mm）

1）结合上文数值模拟塑性区分布规律，留巷塑性区呈非对称分布，塑性区随工作面推进不断往顶板与副帮夹角以及底板和正帮夹角两对角区域扩展，故将巷道顶板及副帮夹角处的锚杆由原来的垂直锚固改进为与垂线夹角呈15°斜向支护，对正帮与底板夹角处锚杆做相同处理，加强锚固巷道顶板与底板两对角处围岩破碎区。

2）鉴于二次采动期间留巷塑性区发生进一步恶性扩展，因此在留巷稳定阶段，在原支护参数基础上进行补强支护。补打锚索规格为Φ22 mm×7 300 mm，锚索间排距为2 000 mm×2 200 mm，每排补打2 根锚索，距两帮最近处1 200 mm。

5 结论

1）通过对留巷进行数值模拟分析，结果显示留巷受重复采动影响，巷道围岩塑性区呈现为非对称破坏。

2）通过理论分析，巷道围岩侧压系数在一定范围时，巷道出现“蝶形”塑性区，围岩塑性区越不规则，巷道稳定性越差。

3）针对巷道围岩塑性区的非对称破坏，提出相应的支护方案，将肩角处的锚杆改为斜向支护，并在留巷稳定期间补打顶板锚索加强顶板肩角处支护，有效控制了顶板大面积冒顶以及帮部片帮问题。