突发台风事件网络舆情预警机制研究*

王建华 朱 敏 郝婷婷 林超英

(江南大学商学院 无锡 214122)

台风是一种高频率、破坏性强的气象灾害,常伴随强降雨,狂风和风暴潮等天气,其带来的洪水、山体滑坡等次生灾害也对人们的生命财产安全造成了极大的威胁。我国是受台风影响最严重的国家之一,每年夏季的台风都会成为高热度话题。更有台风上岸以来,引起的舆论话题在网上愈演愈热,随着情绪的共鸣,公众的恐慌心理不断扩大,严重影响了社会的安定。而一个有效的突发事件网络舆情危机预警机制可以在及时辨别风险等级的同时提高预警响应速度,不仅为政府争取了防范时间,也为政府做出对应措施提供了依据。基于此,本文在建立舆情预警指标体系的基础上,构建了突发台风事件网络舆情预警机制,结合组合赋权方法和SAGAFCM算法,探讨台风发生期间预警机制的变化情况,利用随机Petri网并结合台风“烟花”实际案例进行仿真分析,针对预警机制各指标间的交互影响进行分析,制定预警启动规则。

1 文献综述

目前,国内外关于舆情危机预警研究主要从以下两个方面展开:一是构建预警指标体系:Peng等[1]充分考虑网络舆情的发展特点和传播特点,构建了包括4个一级指标和13个二级指标的网络舆情预警指标体系,并得出该指标体系可行的结论;王英杰等[2]以疫情事件、用户信息行为、情感倾向为一级指标,在实地调查和文献研究的基础上建立了信息疫情下短视频网络舆情指标体系;黄炜等[3]对指标进行筛选,最终得到了一个由7个一级指标,30个二级指标组成网络恐怖事件预警指标体系。二是预警方法设计:在预警指标评价方法方面,杨柳等[4]采用熵权法对指标定权,运用TOPSIS和灰色关联分析相结合的方法构建了高校网络舆情风险评估及预警模型;林玲等[5]提出了一种用直觉模糊数来表达专家对网络舆情风险评估中的不确定因素,用非可加的模糊测度来描述指标间的相互联系,并用 Choquet的直觉模糊积分算子来对各指标的评估信息进行了全面的评估。在舆情预警分类分级方法层面,田世海等[6]在构建指标体系的基础上,运用ABC分类法将指标体系中16个指标进行风险排序,并按照累计发生频率分为Ⅰ-Ⅲ级;杨柳等[7]将指标进行了关联度分析,并以此为基础,利用K均值聚类将舆情事件划分为三个类别,从而获得了不同时间段所对应的警戒级别。

上述研究为突发事件网络舆情危机预警奠定了基础,但还存在不足之处:①对预警指标风险程度进行了探讨,但却忽略了因突发事件的不确定性造成指标风险程度不断变化的情况;②随着研究的深入,网络舆情预警机制应用范围逐渐广泛,但很少有人将预警机制运行机理直观呈现出来,而随机 Petri 网对于复杂系统的仿真建模有很好的呈现能力。现有研究大多将Petri 网应用到应急响应[8-9]、邻避冲突[10]、自然或社会灾害[11-12]、传染病[13]以及网络信息[14-15]的演化和传播等过程中,并对其单一指标进行敏感性分析,但很少有人将Petri 网应用到台风这类突发事件网络舆情危机预警领域。因此,本文在建立指标体系的基础上,应用Petri 网,并根据台风发生不同时期,对指标进行动态分类分级,旨在完善突发事件网络舆情危机预警机制,并在台风来临时,为政府采取防范措施提供决策依据。

2 网络舆情危机预警机制

当今,在大数据环境下,所有信息、事件都处于公开化状态,人们可以在网上畅所欲言,表达自己不同的想法。网络舆情的形成往往十分迅速,一件热点事件再加上人们不同的舆论导向,很容易诱发舆情危机,带来恐慌。因此,建立一套完善的网络舆情危机预警机制是很有必要的:在舆情萌发前期,根据危机预警机制来判断风险,做出相应的预防措施;舆情快速发展并达到高潮时,利用危机舆情机制对风险来进行新的判断,以降低风险,减少损失;舆情逐渐消退但并不代表永远消失,所以要对危机预警机制进行实时监测,防止舆情再次爆发。

2.1 指标选取

为了得到更为全面的指标,本文充分研究了突发事件出现时,网络舆情传播过程中的特点。进一步与文献调查相结合,经过反复筛选的调整,最终建立了如表1所示的包括4个一级指标和16个二级指标的网络舆情预警指标体系。

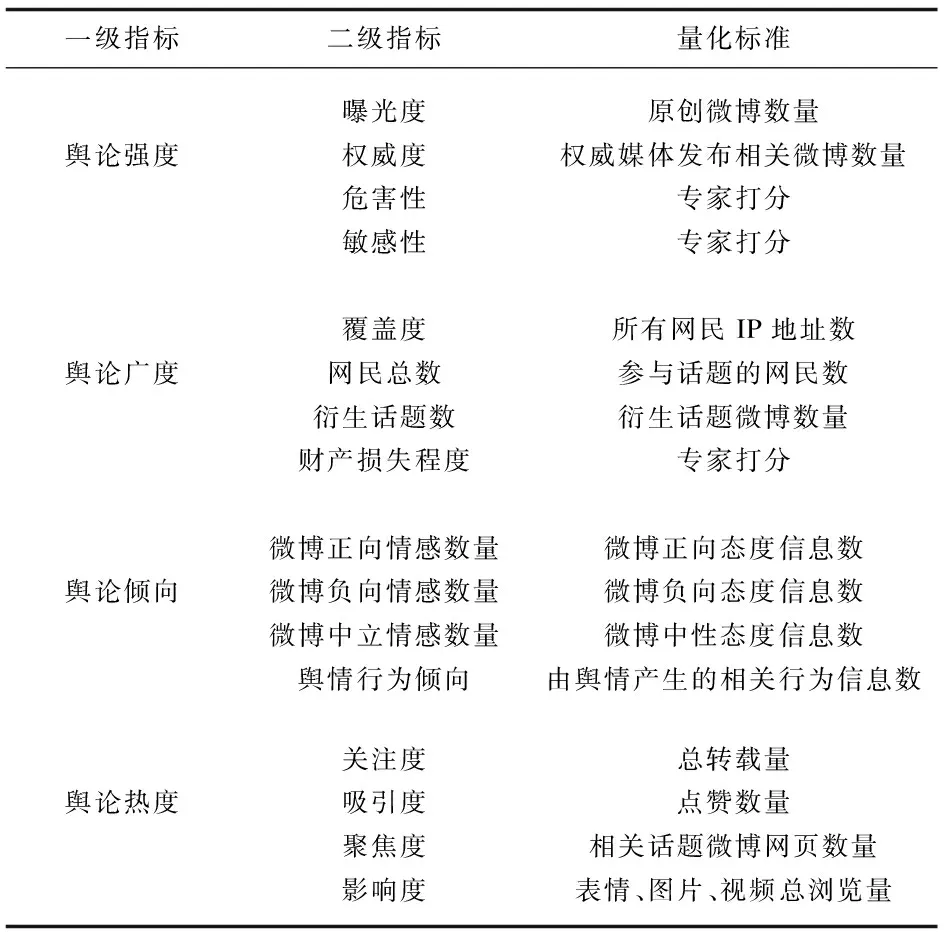
表1 网络舆情预警指标体系

表1中既包括定性指标又包括定量指标。其中利用专家分析与文献研究的方式来获得定性指标,通过搜集与话题事件有关的数据来获取定量指标。其中,敏感度指的是网民对网络舆情的敏感程度,根据专家判断对敏感度指标进行赋值:特别敏感为4、较高敏感为3、一般敏感为2、较低敏感为1;危害性主要衡量网络舆情危害程度,按危害等级赋值,根据黄星等[16]的观点,将发事件危害性赋值为:极高危害值为7、高危害值为5、中等危害值为3、低危害值为1;财产损失程度根据实际数据,按财产损失等级赋值:严重损失赋值5、较严重赋值4、一般严重赋值3、损失较少赋值2、轻微损失赋值1。

2.2 指标定权-分类-分级

在选取指标后,要对指标进行定权-分类-分级处理。由于事件的不确定性和指标的模糊性,该文采用基于三角模糊数的组合赋权方法对指标进行定权处理,首先将一级指标的三角模糊互补矩阵去模糊化后再标准化,得到标准化矩阵,并利用熵权法对一级指标进行定权;其次计算各个二级指标的纯测量度,得到相应的权重;最后将一、二级指标权重进行组合,得到最终的权重。

为了能够及时掌握台风事件网络舆情的动向并对其采取一定的措施,这时就需要对指标进行分类分级处理,根据不同等级采取不同的措施,能够高效解决问题。此篇论文在台风发生前期,利用白化权函数,将指标分为Ⅰ、Ⅱ、Ⅲ、Ⅳ类,并对其进行分级;在台风发生期间,基于模拟退火遗传算法的模糊 C 均值聚类分析方法,在数据采集的基础上对每天的指标进行等级划分。

2.3 建立危机预警机制

要建立一套行之有效的危机预警机制,其各个环节必须紧紧相扣。在台风来临之际,根据经验对指标进行筛选并分级,实时监测,对风险指标,提前做好预防工作,以降低其风险;由于台风的不确定性,指标的风险值也在不断变化,在台风到来期间,根据实际数据,对指标进行新的分级,并实时监测,对新的风险指标,及时采取措施,以降低其风险。其具体流程如图1所示:

图1 突发台风事件网络舆情危机预警机制

3 SPN模型分析

Petri网的概念最早是由卡尔·A·佩特里在20世纪60年代提出的,它可以描述异步、并发事件,既有严格的数学表达方式,又有直观的图形表达方式。一般来说,经典的Petri网由库所、变迁、有向弧和令牌组成,用来刻画过程的简单模型。最早的petri网并没有时间这一概念,但是随着人们对时间概念的需求逐渐增大,便出现了将变迁与随机的指数实施延时相联系的结果,即随机Petri网(SPN)[17]。在台风事件中,时间是危机预警模型的重要参数,所以此篇论文将SPN引入预警机制模型中。

SPN一般由6个要素组成: SPN=(P,T,F,W,M,λ)[18]。其中:

P={P1,P2,…Pn}是库所的有限集合,在此篇论文中表示危机预警要素的有限集合,n为要素的个数,n>0。

T={t1,t2,…ti}表示变迁的有限集合,i大于0;

F⊆I∪O,其中I⊆(P×t),表示变迁输入弧的有限集合。O⊆(t×P),表示变迁输出弧的有限集合。

W:F→N+,表示权函数,对有向弧赋予权重,N+={1,2,…m},m>0。

M:P→M,表示Petri的标识,其中M0表示初始标识。

λ={λ1,λ2,…λn}表示平均点火速率,时间变迁服从负指数分布[19],λ表示分布函数的参数。

把变迁和点火速率相对应,就得到了一个完整的随机Petri网。由于SPN与连续时间马尔可夫链的同构性[20],因此为了得到系统的稳定概率,本文将通过构造SPN同构的马尔可夫链来分析网络舆情问题的启动点。

3.1 Petri网模型

本文利用SPN模型的定义,将图1的网络舆情危机预警机制转化为SPN模型(如图2所示),模型由9个库所和16个变迁组成。

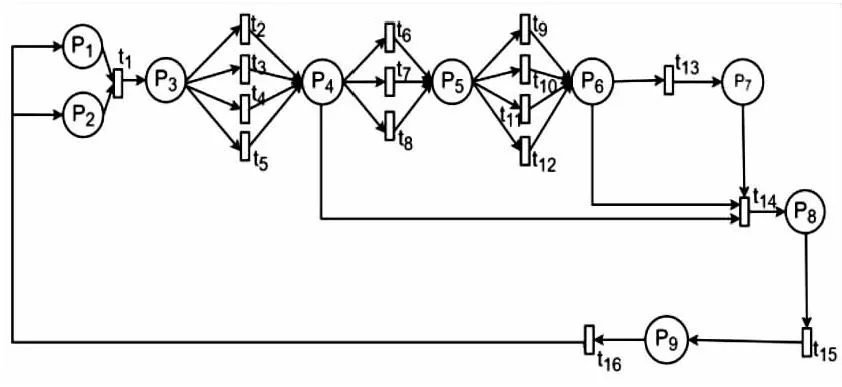
图2 台风事件网络舆情危机预警机制的SPN模型

其中各个库所的含义如下所示:P1为历史数据;P2为实时数据;P3为信息整合;P4为网络舆情萌发;P5为网络舆情扩散;P6为网络舆情加速扩散;P7为网络舆情爆发;P8为危机预警;P9为方案决策。

各个变迁的含义如下:t1为信息过滤;t2为Ⅰ级风险评定;t3为Ⅱ级风险评定;t4为Ⅲ级风险评定;t5为Ⅳ级风险评定;t6为公众情绪感染;t7为谣言大量传播;t8为官方回应不及时;t9为Ⅰ'级风险评定;t10为Ⅱ'级风险评定;t11为Ⅲ'级风险评定;t12为Ⅳ'级风险评定;t13为未及时处理舆论信息;t14为事件升级;t15为预警启动并进行专题分析;t16为监测。

3.2同构马尔可夫链的建立

基于定义,一般有如下步骤:

步骤1,分析SPN模型的可达集:该网络舆情危机预警机制SPN模型的初始标识M0为(1,1,0,0,0,0,0,0,0),即库所P1和P2中各有一个托肯。基于SPN的触发规则[21],可以得到以下可达集:

M0=(1,1,0,0,0,0,0,0,0)

M1=(0,0,1,0,0,0,0,0,0)

M2=(0,0,1,0,0,0,0,0,0)

M3=(0,0,1,0,0,0,0,0,0)

M4=(0,0,1,0,0,0,0,0,0)

M5=(0,0,1,0,0,0,0,0,0)

M6=(0,0,0,1,0,0,0,0,0)

M7=(0,0,0,0,1,0,0,0,0)

M8=(0,0,0,0,1,0,0,0,0)

M9=(0,0,0,0,1,0,0,0,0)

M10=(0,0,0,0,1,0,0,0,0)

M11=(0,0,0,0,1,0,0,0,0)

M12=(0,0,0,0,1,0,0,0,0)

M13=(0,0,0,0,1,0,0,0,0)

M14=(0,0,0,1,0,1,1,0,0)

M15=(0,0,0,0,0,0,0,1,0)

M16=(0,0,0,0,0,0,0,0,1)

步骤2,构建马尔可夫链:根据上述可达集的16个状态M1,M2…,M16构建网络舆情危机预警机制SPN模型等价同构的马尔可夫链,如图3所示。

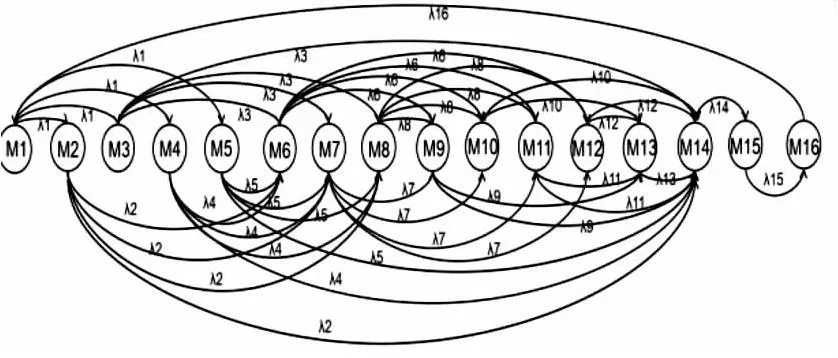
图3 SPN模型同构的马尔可夫链

图3中有向弧代表了该模型从一种状态到另一种状态的转变,其中λj表示变迁的速率(j>0)。设P(Mi),(i=1,2,…,6)为台风事件网络舆情危机预警机制SPN模型处于稳定状态下Mi的概率。将马尔可夫平稳分布相关的定理和切普曼—柯尔莫哥洛夫方程[22]带入图3的马尔可夫链,可得到关系式(1):

4λ1P(M1)=λ16P(M16)

4λ2P(M2)=λ1P(M1)

4λ3P(M3)=λ1P(M1)

4λ4P(M4)=λ1P(M1)

4λ5P(M5)=λ1P(M1)

4λ6P(M6)=λ2P(M2)+λ3P(M3)+λ4P(M4)+

λ5P(M5)

4λ7P(M7)=λ2P(M2)+λ3P(M3)+λ4P(M4)+

λ5P(M5)

4λ8P(M8)=λ2P(M2)+λ3P(M3)+λ4P(M4)+

λ5P(M5)

2λ9P(M9)=λ6P(M6)+λ7P(M7)+λ8P(M8)

2λ10P(M10)=λ6P(M6)+λ7P(M7)+λ8P(M8)

2λ11P(M11)=λ6P(M6)+λ7P(M7)+λ8P(M8)

2λ12P(M12)=λ6P(M6)+λ7P(M7)+λ8P(M8)

λ13P(M13)=λ9P(M9)+λ10P(M10)+λ11P(M11)+

λ12P(M12)

λ14P(M14)=λ2P(M2)+λ3P(M3)+λ4P(M4)+

λ5P(M5)+λ9P(M9)+λ11P(M11)+

λ12P(M12)+λ13P(M13)

λ15P(M15)=λ14P(M14)

λ16P(M16)=λ15P(M15)

(1)

4 案例分析

2021年“烟花”给中国部分地区带来了巨大的损失,这一事件在微博上也引起了很大的反响。本文以台风—“烟花”事件为例,构建了网络舆情危机预警机制模型,并进行仿真分析,最终得到危机预警启动规则。2021年6月18日,“烟花”生成;7月21日,台风进入24小时警戒线,此时台风已经达到强台风级别,郑州出现特大暴雨,多地被淹没,中央气象台发布台风蓝色预警;7月24日,台风本体上岸,浙江上海航班全部取消;7月25日,台风登录浙江,多处地区海水倒灌,浙沪沿海地区呈现巨浪;7月26日,余姚出现暴雨;7月28日,郑州在经历暴雨后又将面临台风,此时微博讨论较为热烈;7月29日,“烟花”二次登录我国,并一路向西北方向行进;7月31日,烟花逐渐减弱,微博热度逐渐减少至消退。7月22日在“烟花”升级为强台风后,其话题热度不断增加,因此本文利用Gooseeker爬取了自7月19日到7月31日微博平台6余万条相关数据。经过去除重复数据、无用数据和干扰字符,最终得到5万余数据。

4.1 指标定权、分级处理

a.采用基于三角模糊数的组合赋权方法对前期指标进行定权处理,并用改进白化权函数进行分级:

步骤1,根据以往文献和专家经验,将一级指标和其对应的二级指标分别进行两两对比,得到相应的三角模糊判断互补矩阵A=(art)m×m和An(n=1,2,3,4),其中art=(artl,artm,artu),artl表示专家给出的保守评价,artm表示专家给出的中性评价,artu表示专家给出的乐观评价。将一级指标的三角模糊判断互补矩阵A去模糊化,然后利用MAX-MIN法对数据进行标准化处理,得到标准化矩阵A’,最后利用熵权法对标准化后的一级指标进行定权,得到权重ω=(ω1,ω2,ω3,ω4)。

步骤2,将各个二级指标的三角模糊判断互补矩阵的行合并归一化,得到权重向量ωij(i,j=1,2,3,4);然后利用公式(2)对应P(ωr≥ωt)求各个指标的纯测量。

(2)

步骤3,确定指标的权重向量。假定任一指标优于其他指标的纯测量度用di表示di=minP(a≥b),

可得各个二级指标的期望权重向量为αj'=(d1,d2,…,dn)。根据归一化公式,得到指标的权重向量αj=(α1,α2,…,αn)。

(3)

(4)

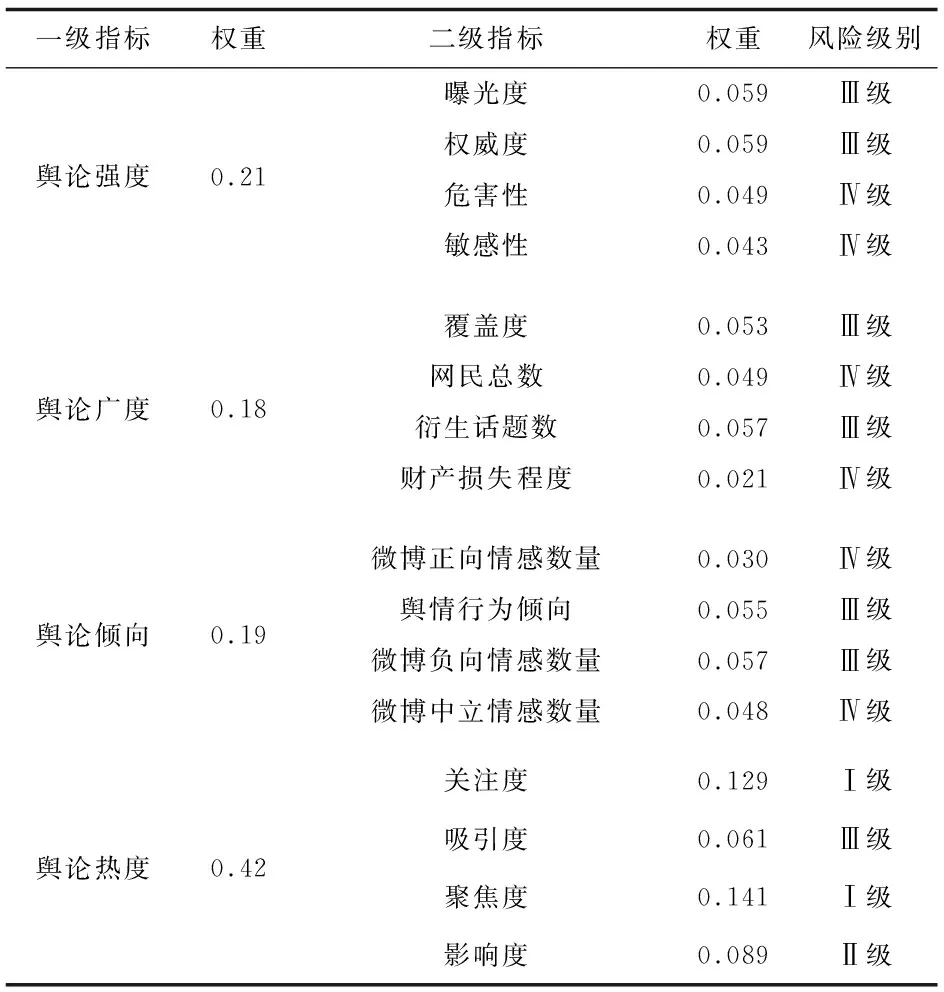
表2 网络舆情预警指标体系评级

(5)

为了及时掌握台风的动向,本文在真实数据的基础上,利用基于模拟退火遗传算法的模糊C均值聚类对数据进行聚类并分级,从表3可知从19日到31日,其指标的风险级别是在变化的,倘若只是将某一指标划分为固定某一风险级别而忽略了它的变化,则可能造成官方得到舆论信息滞后而回应不及时,延长了政府采取措施的时间。

4.2 危机预警仿真分析

分析SPN模型,由表3可知,不同级数的风险指标对台风事件网络舆情危机预警的影响不同,但是其影响程度及各个风险指标之间的相互关系尚不清楚。因此本文用Matlab来对风险指标进行仿真分析,来探究其之间的影响关系。在对数据进行筛选、分析的基础上,得出了相关λ的参数:本文假定数据库以每分钟次的频率进行更新,则λ1=20。根据采集的数据可得知,Ⅰ级、Ⅱ级、Ⅲ级和Ⅳ级风险指标的影响速率分别为9条/分钟、6条/分钟、4条/分钟和2条/分钟,即λ2=9,λ3=6,λ4=4,λ5=2。与此同时,公众情绪倍受感染(λ6)、谣言大量传播(λ7),官方回应不及时(λ8),假设λ6=4,λ7=5,λ8=1。根据所搜集的数据可知,Ⅰ'级,Ⅱ'级、Ⅲ'级和Ⅳ'级风险指标的影响速率分别为1条/分钟、0.5条/分钟、0.2条/分钟和0.1条/分钟,即λ9=1,λ10=0.5,λ11=0.2,λ12=0.1。随着台风的不断影响,再加上政府以及官方未及时处理舆论信息(λ13),导致事件升级(λ14),最终启动预警机制并且对此时形势进行专题分析,不妨设λ13=10,λ14=7,λ15=1。启动预警机制后,

系统对数据不断进行更新处理,即监测(λ16)(假设系统对数据2分钟进行一次监测,即λ16=2),以便风险不断变化而采取不同措施。

4.2.1一级风险指标对稳态概率的影响

在保持其他λ值不变的情况下,分别分析λ2、λ9和各状态稳态概率的关系。 图4(a)是Ⅰ级风险指标实时值对各个稳态概率的仿真结果,图4(b)是Ⅰ'级风险指标实时值对各个稳态概率的仿真结果。通过两图对比分析可知:Ⅰ级风险指标实时值对危机预警启动概率(P(M15))影响较小,其曲线较为平稳。而Ⅰ'级风险指标实时值对危机预警启动概率影响相对较大,其曲线整体波动较大,随着λ9参数的不断增大,其概率也从0.32上升到0.38。

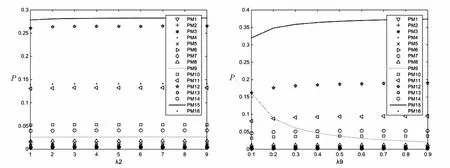
(a) (b)图4 Ⅰ级风险指标和Ⅰ'级风险指标实时值对稳态概率的影响

4.2.2二级风险指标对稳态概率的影响

在保持其他λ值不变的情况下,分别分析λ3、λ10和各状态稳态概率的关系。图5(a)是Ⅱ级风险指标实时值对各个稳态概率的仿真结果,图5(b)是Ⅱ'级风险指标实时值对各个稳态概率的仿真结果。通过两图的对比分析可知:Ⅱ级风险指标实时值对危机预警启动概率(P(M15))影响较小,其曲线较为平稳。而Ⅰ'级风险指标实时值对危机预警启动概率影响相对较大,其曲线波动较大,随着λ10参数的不断增大,其概率从0.33上升到0.39。

(a) (b)图5 Ⅱ级风险指标和Ⅱ’级风险指标实时值对稳态概率的影响

4.2.3三级风险指标对稳态概率的影响

在保持其他λ值不变的情况下,分别分析λ4、λ11和各状态稳态概率的关系。 图6(a)是Ⅲ级风险指标实时值对各个稳态概率的仿真结果,图6(b)是Ⅲ'级风险指标实时值对各个稳态概率的仿真结果。通过两图的对比分析可知:Ⅲ级风险指标实时值对危机预警启动概率(P(M15))影响较小,其曲线较为平稳。而Ⅲ’级风险指标实时值对危机预警启动概率影响相对较大,其曲线波动较大,随着λ10参数的不断增大,其概率从0.34上升到0.41。

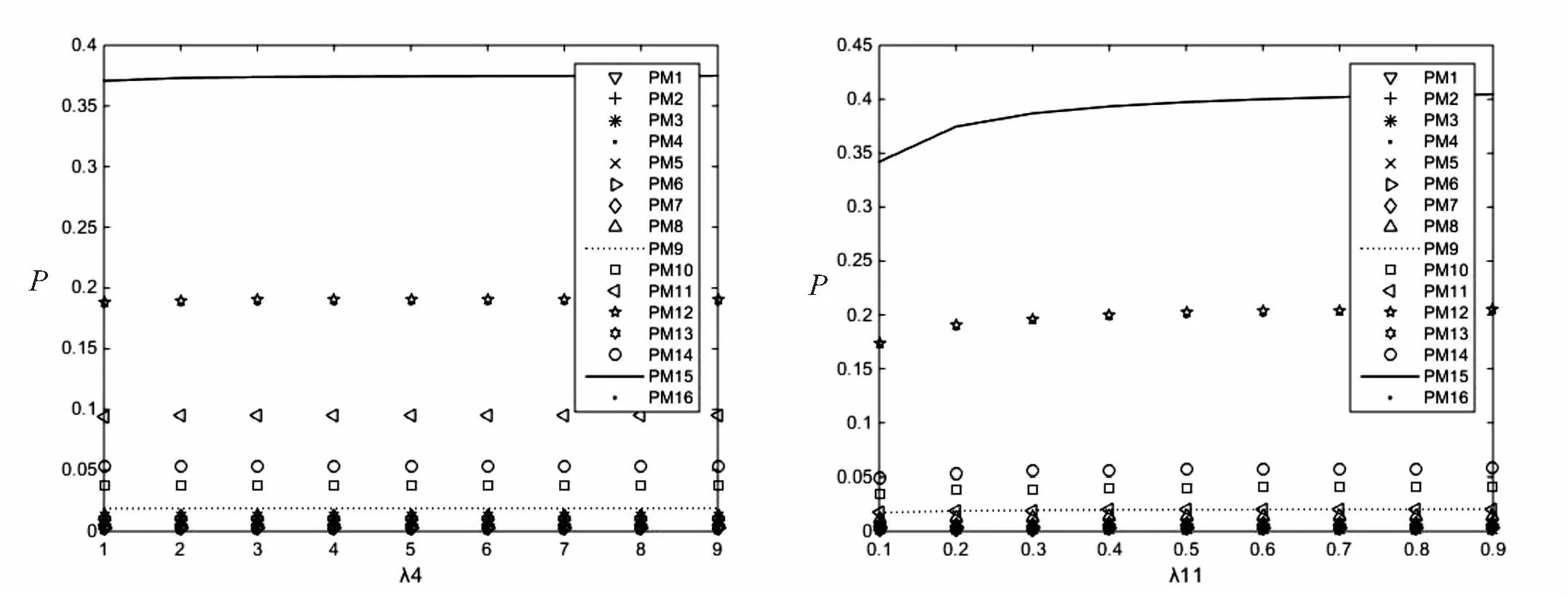
(a) (b)图6 Ⅲ级风险指标和Ⅲ'级风险指标实时值对稳态概率的影响

综上所示,台风期间对数据进行监测分析后得到的风险指标分级实时值对预警启动概率影响程度更大。台风的不确定性因素造成了各级指标风险级别的不断变化(有些台风前期Ⅳ级指标可能会随着台风发生危险级别逐渐上升),若只关注台风前期各级指标实时值的影响,可能会出现把Ⅰ级风险当作Ⅳ级指标来处理,那么就会导致信息滞后,官方回应不及时,最终延长预警的启动时间。这不利于舆论消息的及时处理,同时对危机预警机制的实施也有一定的影响。因此,要将台风发生前的风险指标和台风发生期间的风险指标实时值同时监测,及时分级,根据危机预警机制及时采取相应措施。

4.3 危机预警启动

由上结果可知,仅仅分析台风前期指标级别与危机预警启动的概率,容易造成预警响应时间的延长而错过最佳决策的时间。为了缩短预警响应时间,本文研究了台风发生前期Ⅰ级、Ⅱ级指标与危机预警启动概率的关系以及台风发生期间Ⅰ'级、Ⅱ'级指标与危机预警启动概率的关系。同时对Ⅰ'～Ⅲ'级指标实时值交互关系进行仿真分析,得到了预警临界曲面。为预警启动提供了依据。

由图7可知,保持除λ2、λ3以外的参数不变,利用公式(1)得到Ⅰ级Ⅱ级指标与预警启动概率的关系式:

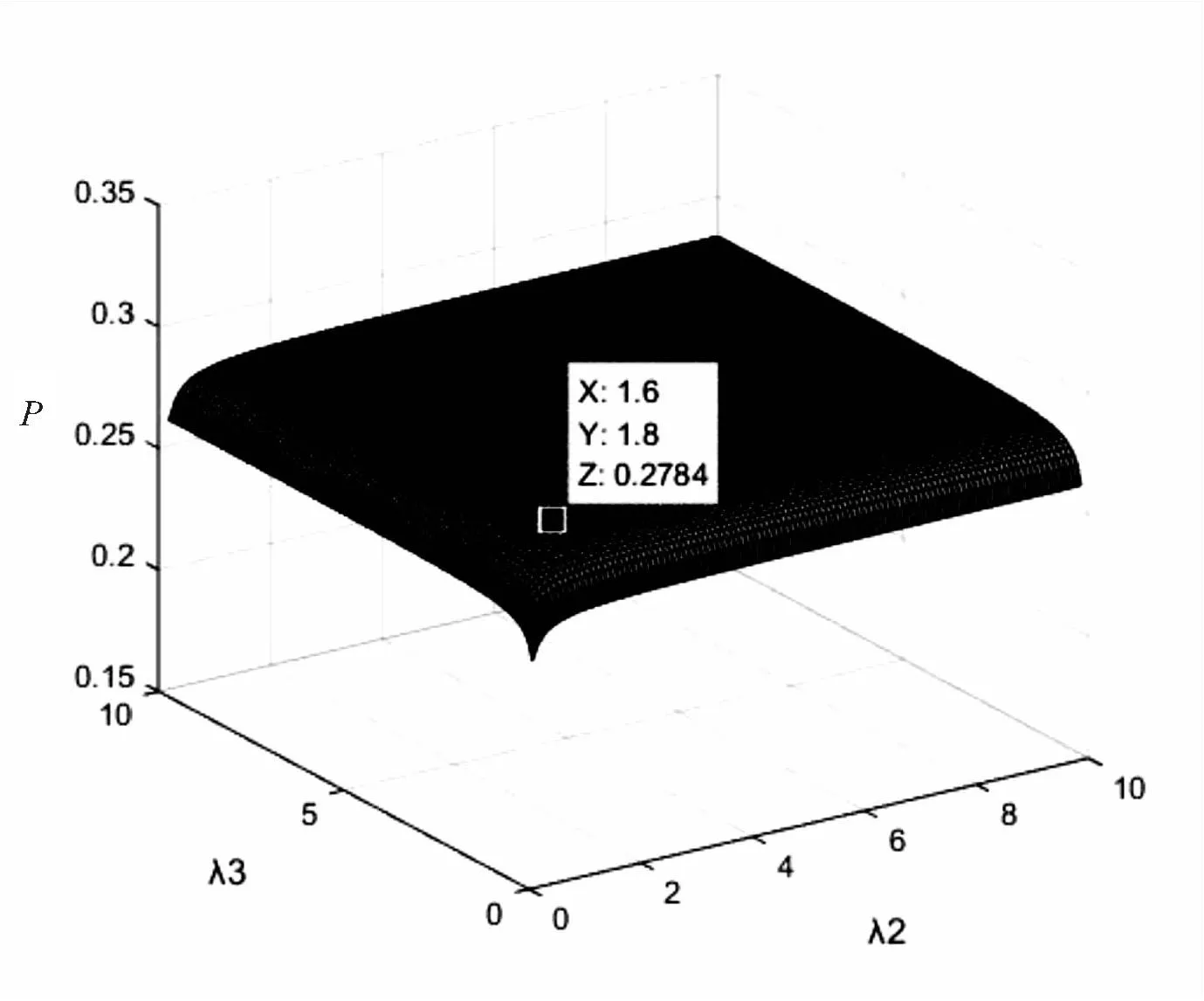
图7 λ2和λ3与危机预警启动概率关系图

其中,p表示危机预警启动的概率,λ2、λ3分别表示Ⅰ级、Ⅱ级指标实时值。如果设预警启动阈值为0.1,则当λ2=1.6,λ3=1.8时,危机预警启动概率为27.84%,此时系统进入警戒状态,根据评级系统,自动开启对应级数警报,在台风发生前期,政府根据报警级数及时做好预防工作,减少损失。

在做好预防工作的同时,应监测实时数据,根据台风发生期间收集的数据进行重新分类分级,分析Ⅰ'级、Ⅱ'级指标与危机预警启动概率的关系。如图8所示,保持除λ9、λ10以外的参数不变,利用公式(1)得到Ⅰ级Ⅱ级指标与预警启动概率的关系式:

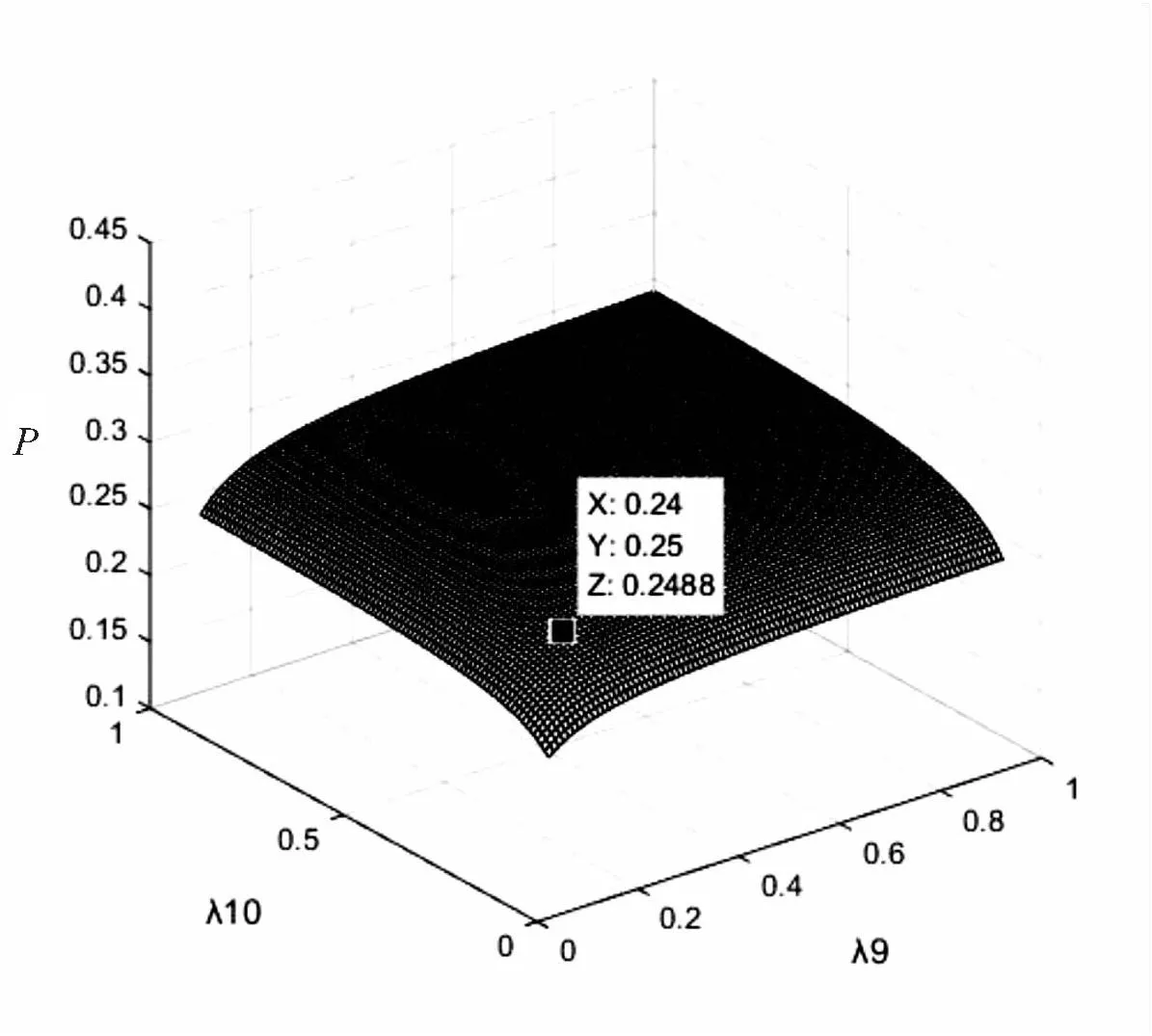
图8 λ9和λ10与危机预警启动概率关系图

其中,λ9、λ10分别表示Ⅰ'级、Ⅱ'级指标实时值。当λ9=0.24,λ10=0.25时,危机预警启动概率为24.88%,此时系统进入警戒状态,根据评级系统,自动开启对应级数警报,在台风发生期间,政府根据报警级数及时采取措施,做出官方回应。

Ⅲ'级指标虽然影响不大,但是也不能忽略其值的增长。故本文根据Ⅰ'～Ⅲ'级指标实时值交互关系来分析是否达到预警曲面临界值。如图9所示,当λ9=0.13,λ10=0.47,λ11=0.2455时达到预警临界曲面,此时启动警报。曲面以下表示未启动预警,离曲面以下越远其启动概率越小。当三者交互达到临界曲面值时则应采取相应措施。

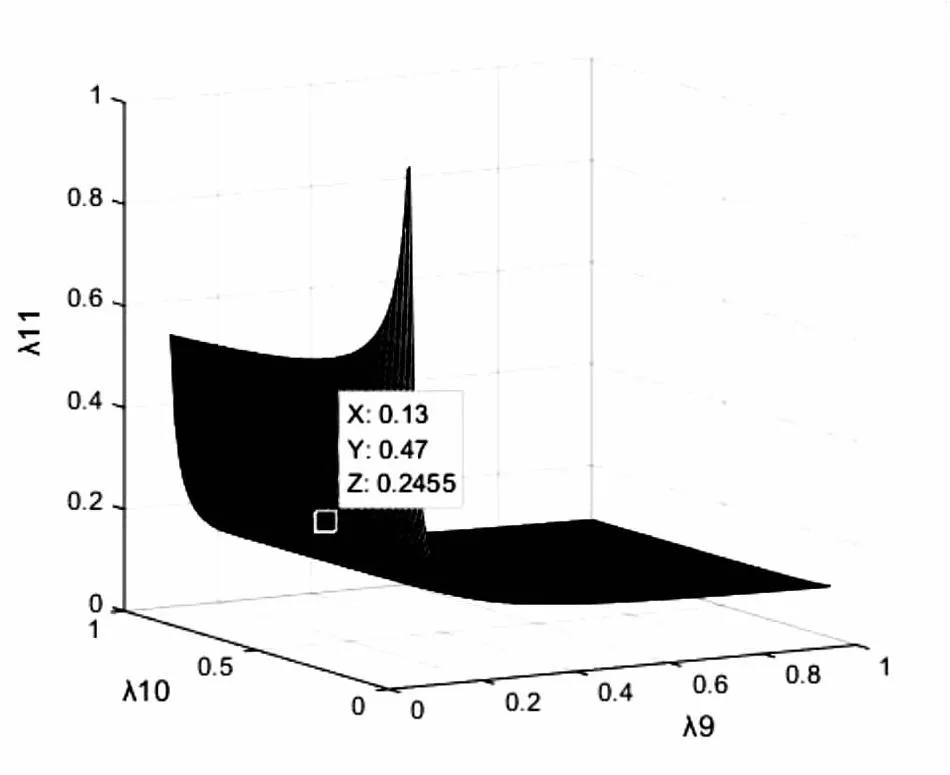
图9 Ⅰ'～Ⅲ'标实时值变动下预警临界曲面

若将预警启动阈值设定为0.1,则:当预警启动概率p∈[0.1,0.2)或者达到交互影响产生的临界曲面,则启动蓝色警报;当预警启动概率p∈[0.2,0.3)或者达到交互影响产生的临界区面,则启动黄色预警;当预警触发概率p∈[0.3,0.4)或者达到交互影响产生的临界曲面,则启动橙色预警;当预警启动概率p≥0.4时,则启动红色警报。

按照预警触发相关规则,通过对上述参数计算得出21日“台风烟花事件”发生预警警报几率是最大的,为p=0.481>0.4,故启动红色预警。而由图10可知,7月21日舆情态势达到了最高峰,这与本文的研究相符。

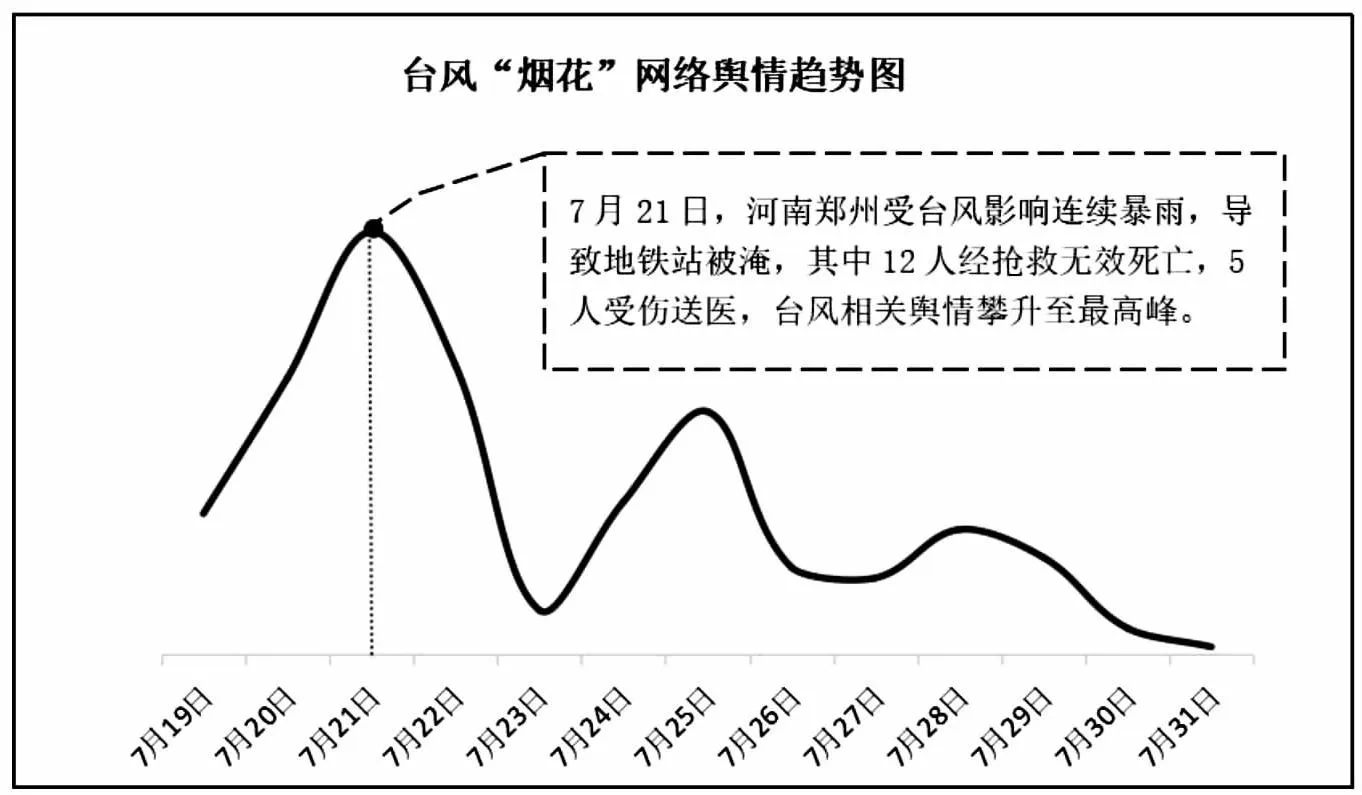
图10 台风“烟花”网络舆情态势

5 结 语

本文基于舆情指标体系的建立,构建了行之有效的突发台风事件网络舆情危机预警机制并对其进行仿真分析,制定了危机预警启动规则。

a.面对台风风险等级不断变化的情况,本研究在台风发生前,采用组合赋权法对指标进行分类分级,在台风发生期间,利用SAGAFCM算法将处理好的指标数据进行聚类,分别得到不同的四级风险指标(Ⅰ～Ⅳ级风险指标和Ⅰ'～Ⅳ'级风险指标),并根据风险指标级别的强弱制定网络舆情危机预警机制,为台风这类突发事件网络舆情预警提供了理论依据,且指标风险实时更新,丰富了舆情预警机制的研究。

b.利用随机Petri网与马尔可夫链同构思想,分析关于台风“烟花”事件网络舆情危机预警机制,通过MATLAB仿真得到Ⅰ'～Ⅲ'级风险指标的交互关系,为突发台风事件网络舆情预警提供决策支持。具体决策为:在台风发生前期,根据Ⅰ级,Ⅱ级和Ⅲ级指标实时值判定预警机制处于危机的概率,若此时概率超过了临界曲面值,则启动相应级别预警,否则监测台风发生期间Ⅰ'～Ⅲ'指标实时值;若Ⅰ'级、Ⅱ'级和Ⅲ'级指标实时值超过了预警临界曲面值,则启动相应级别预警,否则监测Ⅰ'级、Ⅱ'级和Ⅲ'级风险指标的交互影响;若这三个指标交互作用达到了预警临界曲面值,则启动对应级别预警,否则重新对系统进行监测。

本文建立了突发台风事件网络舆情预警机制,拓展了突发事件预警机制的研究领域,为政府部门采取应对措施提供了决策依据。另外,由于台风事件属于突发性事件,其具有不确定性和多变性,并没有一套统一、权威的网络舆情指标体系,未来的研究可以从指标体系的构建进行探讨。