利用伸缩变换解决一类面积问题
浙江大学附属中学丁兰校区 俞忠有 施刚良 (邮编:310021)
圆锥曲线在高中数学中是一类非常重要的曲线,每年的数学高考中都是重点考查的,很多一线数学老师也都喜欢对它们作一些研究,得到一些非常优美的结果.数学大师丘成桐先生在成功证明卡拉比猜想后,接受采访时谈过自己的感受:落花人独立,微雨燕双飞.老师们得到的优美结论有些可能是再发现,并不一定是原创的.尽管得到结论的境界没丘先生这么高,但彼此的心情和感受是相通的.
最近,仔细研究了文[1]、[2]、[3]、[4],站在“巨人”的肩膀上,感觉应该可以做一些工作.受文[4]的启发,得到了与文[4]类似的面积关系.下面先给出探究结果:
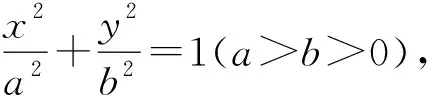
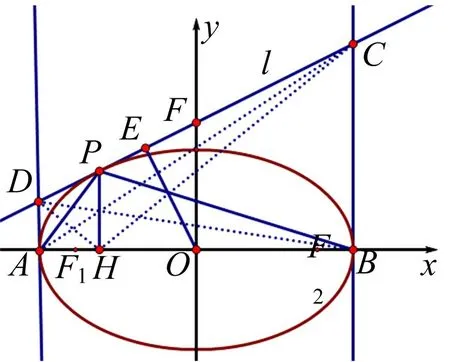
图1
注(1)上述命题中,将椭圆换成双曲线结论仍旧成立.
(2)在文[5]中,还有关于面积的两个结论:
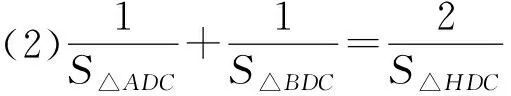
在给出命题的证明之前,先给出下列引理[5]:
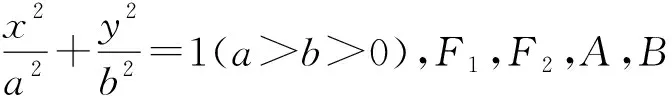
注上述引理中,将椭圆换成双曲线结论仍旧成立.
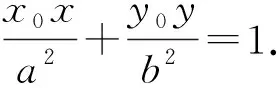
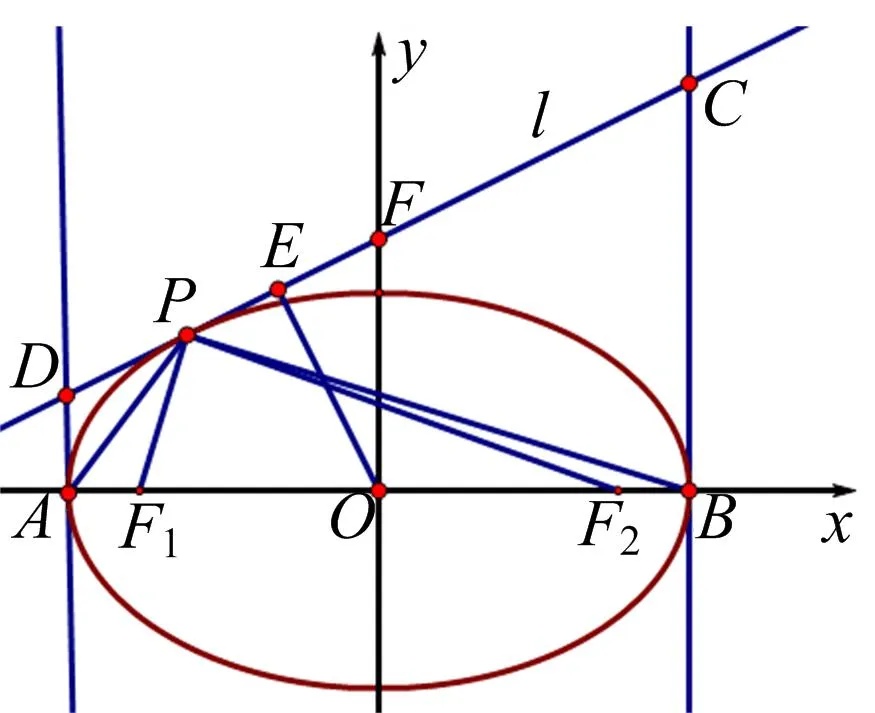
图2
下面给出命题1的两种证明:
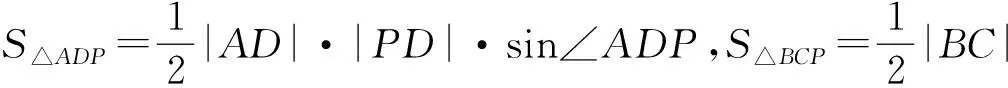
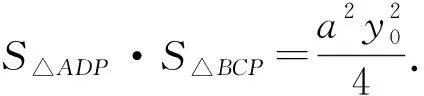
因此,4S△ADP·S△BCP=(S△ABP)2.
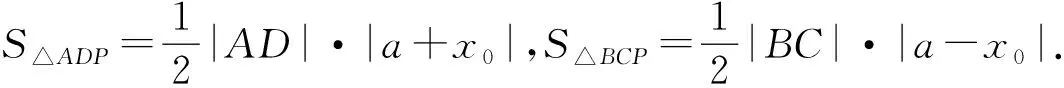
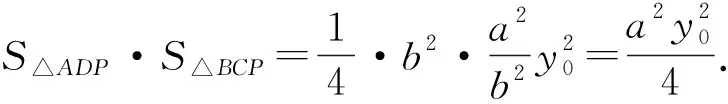
因此,4S△ADP·S△BCP=(S△ABP)2.
评注命题1给出两种证明方法,证法一稍显麻烦,用到很多参考文献中的结论;证法二相对简洁一点(但也用到了引理),主要还是与后面的证明作对比.如果将命题1的结论推广,上面的两种证法就不具有一般性,这也凸显伸缩变换的威力所在.
著名数学家波利亚曾经说过:当你找到第一个蘑菇或作出第一个发现后,再四处看看,它们总是成群生长的.探究到这里还是感到意犹未尽,圆锥曲线的中很多结论都可以进一步推广,有些结论还具有深刻的射影几何背景.上面命题1的结论还是太特殊,于是想对命题再深挖一下,进一步推广.考虑到过中心的弦在有心圆锥曲线里叫做直径,于是就猜想下列结论是否也成立?通过几何画板测试面积关系,发现结论是正确的.
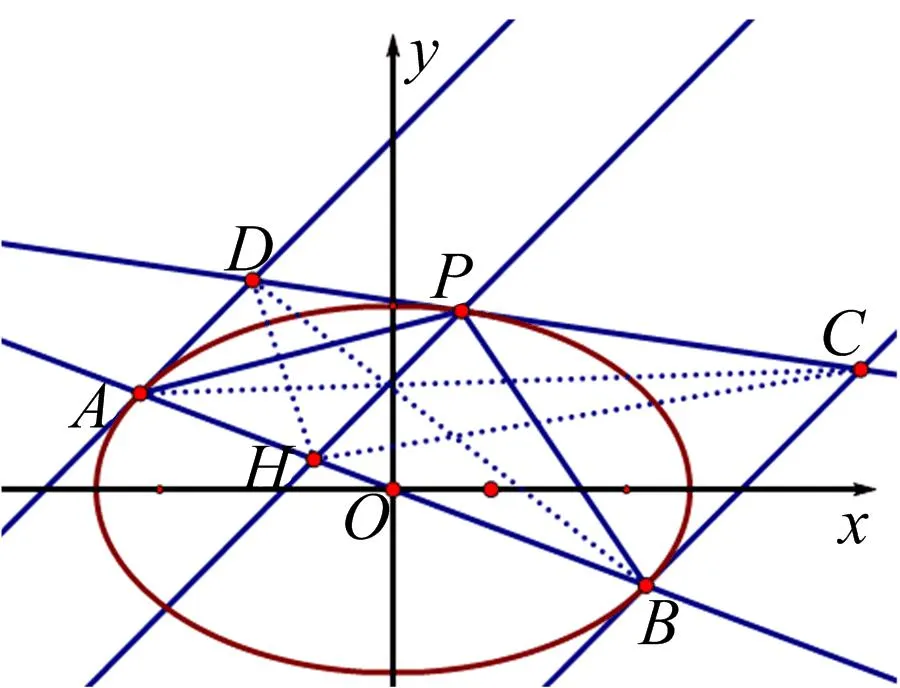
图3
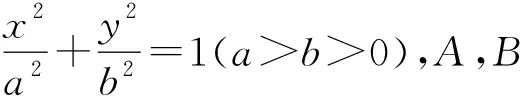
(1)4S△ADP·
S△BCP=(S△ABP)2;
评注命题2可以通过将几何问题代数化加以解决,但是计算过程相对繁琐,可能还不一定能算出来,吃力不讨好!受文[6]、[8]的启发,如果采用高观点的思想,椭圆可以通过圆“压缩”而得到,反之也成立.而且通过这样的变换,面积保持线性比例关系:ST1=abST2(其中椭圆中图形T1是通过圆中的图形T2变换得到的).于是,可以通过考虑圆中的面积关系,来得到椭圆中的面积关系.因为圆中的面积关系计算相对容易,这样就可以达到以简驭繁.
通过上面的思考,将椭圆变换为圆,要证命题2,我们只要证明命题3即可.下面叙述圆中的命题:
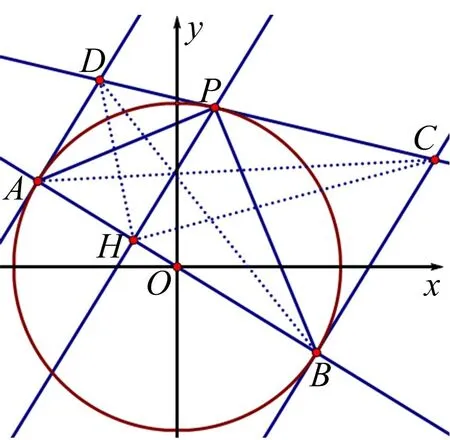
图4
命题3已知圆x2+y2=1,AB是圆的直径,P是圆上的任意一点,过P作圆的切线l,过点A,B分别作圆的切线交l于D,C,过P作AD的平行线交AB于H,则
(1)4S△ADP·S△BCP=(S△ABP)2;
(1)的证明设∠DCB=θ,AD=DP=m,CB=CP=n,则
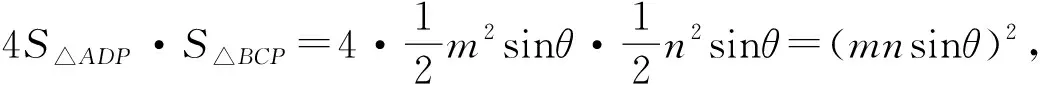
所以4S△ADP·S△BCP=(S△ABP)2.
(2)的证明AP2=2m2+2m2cosθ,BP2=2n2-2n2cosθ,AB2=AP2+BP2=2m2+2m2cosθ+2n2-2n2cosθ.
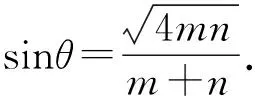
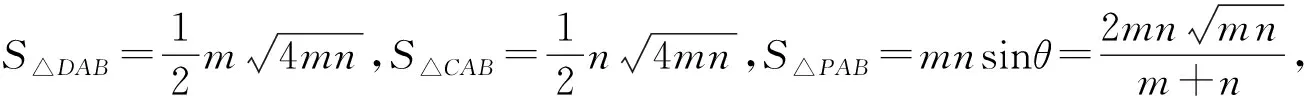
(3)的证明因S△DAB=S△ADC,S△CAB=S△BDC,S△PAB=S△HDC,故由(2)得(3)成立.
评注证完(2)(3)后,出于美学考虑,笔者就想S△ADP,S△BCP,S△ABP是否有像(2)(3)的形式?于是,通过计算发现:
尽管没有达到成功(得到整齐划一的结论),但这个不等式也算是对上述结论的一种补充!
上面的探究基本告一段落,伸缩变换在解决面积问题方面的优势可见一斑.笔者在翻看文[7]时,发现其证明过程略显繁琐,于是就想能否利用伸缩变换简化证明过程?通过探究发现,利用伸缩变换证明过程确实变得很简洁,足见思考问题观点的改变,可以促进问题更好地解决.
先呈现文[7]的两个结论:
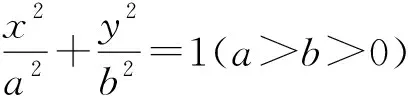
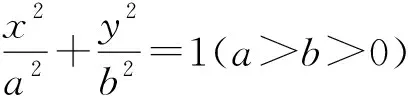
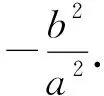
通过伸缩变换,将上述性质1、2分别变为性质3、4:
性质3如图5,在直角坐标系xOy中,已知圆x2+y2=1的一对相互垂直的直径为AC,BD,P是圆上与B,C不重合的一动点,直线PB与直线AC交于点M,直线PC与直线BD交于点N,则S△ABM=S△CNM.
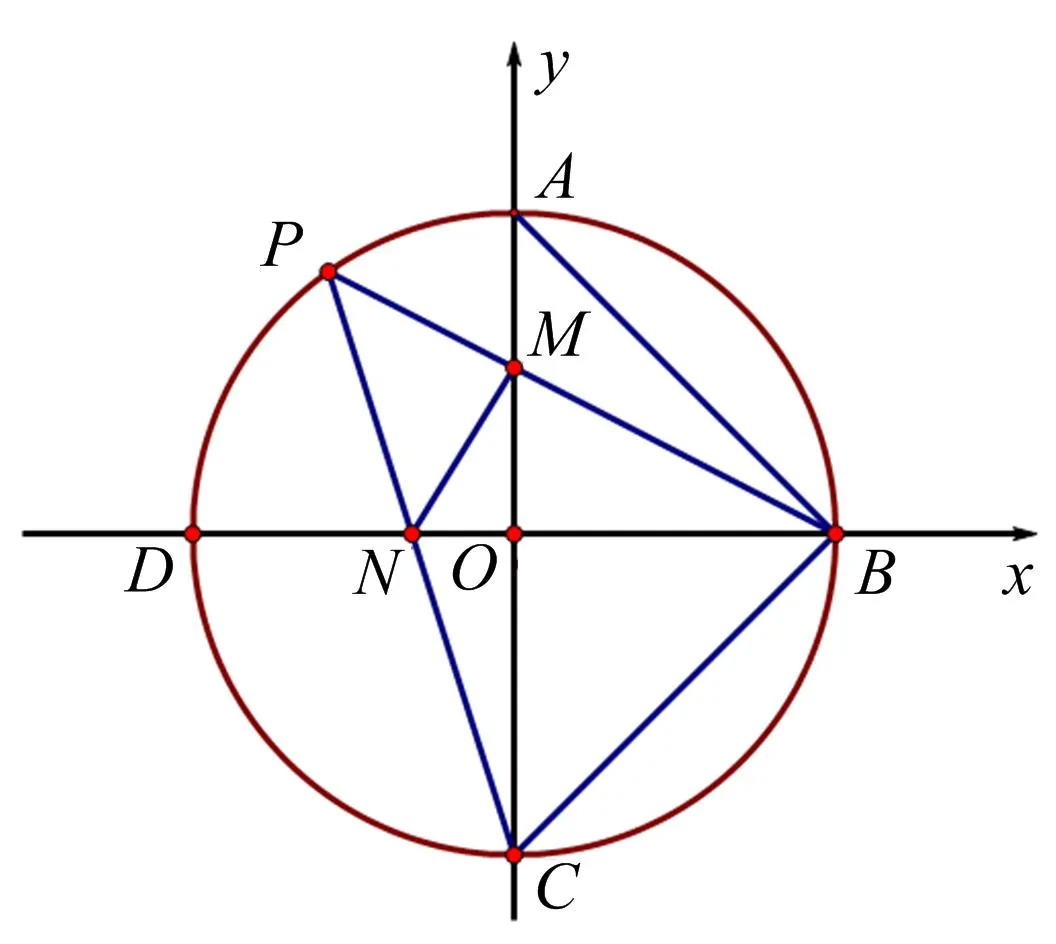
图5
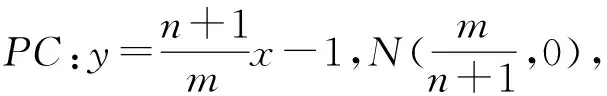
所以S△CNM=S△ABM
⟺(1-n)(1+n-m)=-m(1-m-n)
⟺m2-m+mn=m2-m+mn(显然成立).
性质4如图6,在直角坐标系xOy中,已知圆x2+y2=1的一对相互垂直的直径为AC,BD,P是圆上与A,C不重合的一动点,过点B且与AC平行的直线记l,过点A且与BD平行的直线与直线l交于点Q,直线PA与直线l交于点M,直线PC与直线BD交于点N,则S△AMQ=S△OCN.

图6
证明由题意,易证:△AMQ与△OCN全等,故S△AMQ=S△OCN.
评注通过伸缩变换,将椭圆中的两条共轭直径变换为圆中互相垂直的两条直径,发现证明的过程大大简化,特别是性质4证明达到显然的程度!
当下,在数学课堂教学、教师培训等活动中,比较流行用高观点的数学思想方法解初等数学的问题,这是一件很有创意的工作.高观点(此文指伸缩变换)的核心是站得高、看得远,数学核心素养本质上就是一种高观点,所以采用高观点解决问题能有效提升学生的数学核心素养.
在研究椭圆问题时,有时问题会变得非常复杂(主要是运算问题),位置关系或面积关系用代数方程刻画也将变得异常困难.本文得到的命题若直接计算,计算量非常大,而且还不一定能算出来.通过伸缩变换,将椭圆问题转化为圆的问题,使得问题的解决变得相对容易,让人感觉数学的简洁美.在具体的教学实践中,可以给学有余力的学生介绍伸缩变换,应该也不难掌握,这样他们又多了一种“武器”,碰到类似问题解决起来就会变得游刃有余.
数学不仅仅是一种重要工具,更是一种思维方式、一种思想,能用高观点解决的数学问题在本质上考查的是数学思想方法,而且其本质都显得很简单[9].在具体的教学实践中,应该向学生介绍这些思想在求解具体问题中的应用,就能直奔问题的本质,问题的解决也将变得非常容易.让学生体会解题过程中所采用“观点”的高度,但又不是可望而不可及的,让他们有所“感悟和感叹”,使得他们产生“跃跃欲试”的感觉.

