基于粗粒化分子动力学的自支撑石墨烯镜面屈曲研究*

续文龙 开玥 张锴 郑百林†

1) (同济大学航空航天与力学学院,上海 200092)

2) (上海工程技术大学数理与统计学院,上海 201620)

1 引言

在石墨烯通过机械剥离方法被制备出之后[1],许多研究者将研究关注点从理论分析转向实验观测探索,从力学[2-6]、热学[7-10]、光学[11,12]、电磁学[13-17]以及实际应用转化[18-21]的角度对石墨烯开展全面深入的分析研究,探索这种二维材料独特的性质.除了对石墨烯物理性质开展研究工作之外,通过电子显微镜对石墨烯膜表面观测的工作也有所增加.Neek-Amal等[22]在通过扫描隧道显微镜(scanning tunneling microscopy,STM)对自支撑石墨烯进行实验观测时发现,隧穿电流和偏压在一定范围内时,石墨烯膜在STM探针的牵引下在面外高度产生突跳,并将这种现象称为“热镜面屈曲”(thermal mirror buckling),如图1所示.

图1 热镜面屈曲现象的实验观测——不同隧穿电流下石墨烯面外高度随电压变化曲线,其中黑色曲线对应镜面屈曲现象[22]Fig.1.Experimental observation of thermal mirror buckling.Constant-current feedback-on,Z(V) data sets on suspended graphene acquired using the labeled setpoint currents.The 4.0-nA curve (black) shows the mirror buckling phenomenon[22].

在实验观测到二维材料石墨烯具有这样的特殊现象之后,不少学者们采用理论分析及仿真计算的方法对其进行研究分析.Schoelz等[23]研究发现石墨烯膜在STM探针静电-热作用下产生的面外高度的变化与半自旋伊辛磁场系统具有类似模式.石墨烯产生的不可逆高度突变与铁磁-反铁磁相变有所对应.Ruiz-García等[24]考虑一个简单的自旋-膜模型对具有波纹的石墨烯屈曲以及对其松软到坚硬状态的转变进行定量分析.该模型在非平衡条件下发生的一阶相变与实验中石墨烯膜与STM探针的相互作用类似.Schoelz等[23]利用分子动力学(molecular dynamics,MD)方法对镜面屈曲现象进行定性分析.之后,Xu等[25]使用宏观和微观的方法来探索研究石墨烯热-机镜面屈曲现象合适的分析途径.利用连续介质力学、分子结构力学和分子动力学方法分别对机械载荷和热载荷作用下的石墨烯膜进行计算,对比结果表明,MD方法计算得到的石墨烯面外高度变化与Neek-Amal等[22]在实验中获得的数据及相关仿真结果更加接近.由此可见,MD方法是一种可靠有效地分析石墨烯膜镜面屈曲现象的途径.

然而需要注意的是,无论是在发现石墨烯镜面屈曲的STM实验中[22],还是其他分析石墨烯跳跃失稳(snap-through buckling)现象实验[19,26,27]中,其石墨烯的典型尺寸均为微米级或次微米级,而之前MD仿真计算[25]的模型尺寸为纳米级.考虑到尺度效应可能对石墨烯的力学[28,29]以及热学[30,31]性质带来影响,同时利用石墨烯跳跃失稳现象进行能量收集装置的设计研究[19]中石墨烯的典型尺寸也为微米级,因此有必要在MD方法之外,使用其他方法研究微米级尺寸石墨烯膜的镜面屈曲现象以及不同因素对其产生的影响.

本文采用粗粒化分子动力学(coarse-grained molecular dynamics,CGMD)方法构建石墨烯模型,对于扇形截面不同高跨比的石墨烯膜,分别施加机械载荷和热载荷,研究载荷种类、载荷大小以及模型高跨比对于镜面屈曲现象的影响.探索分析各个因素对于石墨烯镜面屈曲现象的影响有助于研究其产生机理,并为能量收集装置的开发设计提供指导.

2 粗粒化自支撑石墨烯模型及模拟方法

2.1 粗粒化分子动力学方法

CGMD在单层及多层石墨烯的力学性能计算中有着广泛的应用[32-35].本文采用CGMD方法对石墨烯进行建模,通过调整势函数参数,实现粗粒化模型与全原子模型(all-atom model)保持相近的模量以实现使用少量粒子等效大尺寸模型的目的.

粗粒化放大倍率可以根据需求进行选择.本文中倍率选择4∶1,即1个粗粒化珠子(简记为珠子)代表4个碳原子,珠子间距离为2.84 Å,如图2所示.粗粒化模型中珠子质量m可以根据全原子模型中原子质量得到,具体如下:

图2 CGMD模型示意图.黑色圆点表示全粒子模型中的碳原子,蓝色圆点表示CGMD模型中的珠子.红色虚线区域表示碳原子与珠子的典型等效方式Fig.2.Schematics of the CGMD model.The black dots indicate carbon atoms in the all-atom model.The blue dots indicate beads in the CGMD model.The region marked with rad dotted lines express a typical equivalent mode with carbon atoms and beads.

其中d0表示珠子之间距离,dcc表示碳-碳键之间的距离1.42 Å,mc表示碳原子的相对原子质量12.

CGMD模型中键长、键角、二面角以及非成键相互作用的势能总和U表示为

其中Eb,Eα,Ed和Enb分别对应键长、键角、二面角以及非成键相互作用对应的势能;d表示键长大小;θ表示键角大小;ϕ表示二面角大小;r表示两个非成键珠子之间的距离.这几种能量形式的具体函数表达式[33]如下所示:

其中D0和α表示Morse势中与拉伸下非线性行为相关的参数,对于小变形来说,Eb可以近似地写为Eb(d)≈kb(d-d0)2,其中kb=D0α2;kθ表示键角相互作用的弹簧常数;θ0表示平衡键角;kϕ表示二面角的弹簧常数;εLJ表示非成键相互作用Lennard-Jones势阱深度;σLJ表示Lennard-Jones中与两个非成键珠子间距相关的参数.各参数由石墨烯的杨氏模量、剪切模量、弯曲刚度、粗粒化珠子之间键的失效应变以及单位表面积的附着力计算得到,具体数值[32]如表1所列.

表1 CGMD化模型力场参数Table 1.Parameters of the CGMD model force field.

通过这些参数建立的粗粒化石墨烯模型可以有效且准确地反映全原子石墨烯模型的受到载荷作用后的响应.根据这些参数构建的粗粒化模型在单层及多层石墨烯的拉伸、剪切、纳米压痕仿真实验中,在多层石墨烯的层间剪切响应、单轴拉伸破坏响应以及温度和缺陷对拉伸变形的影响等仿真实验中得到广泛应用[32,33].这样的一组参数同样适用于处理STM实验中发现的在面外载荷作用下出现的镜面屈曲现象.

2.2 CGMD方法验证

为了确保CGMD方法在研究石墨烯镜面屈曲现象中的适用性,首先参考实验设置,对STM实验中观测到的镜面屈曲现象[22]进行仿真计算.方形石墨烯模型两边长分别为100.25 nm和100.35 nm,如图3(a)所示.四边自由,与实验中自支撑状态对应.边界条件设为周期性,符合实验中无限大条件.时间步长1 fs,系综为NVT,使用Nose-Hoover热浴法控温.温度设置为300 K,与实验中室温状态接近.通过deform命令将石墨烯沿两边方向分别压缩长度的2%左右,之后进入弛豫.充分弛豫0.5 ns达到能量平衡之后,可以观察到石墨烯出现明显的凸起(或凹陷)变形,如图3(b)所示.凸起(凹陷)状态下在中心位置向下(向上)每隔0.3 ns增加6.946×10-4nN的载荷,使石墨烯在受到逐渐增大的载荷的同时保持稳定,并观测其中心高度随载荷变化曲线.本文通过直接施加机械载荷与实验中的静电载荷对应.

图3 石墨烯粗粒化模型示意图,其中黄色区域表示中心位置 (a)初始状态;(b)中心凹陷状态Fig.3.Diagrams of CGMD graphene models,where the yellow region is located in the center: (a) Initial state;(b) concave region in the center.

通过计算结果与实验数据的对比可知,CG MD计算得到的曲线(如图4)与STM实验中观测到的镜面屈曲现象(图1中黑色曲线)十分相近,同样具有3个典型阶段,即凹陷回升阶段、平稳阶段和反向上升阶段.分别对应原本凹陷的石墨烯在载荷作用下挠度逐渐增大,直到恢复到零高度初始位置,之后在载荷的牵引下进一步升高的过程.值得注意的是,计算及实验结果中第2阶段出现相对平缓的区域可能是由于石墨烯悬浮状态的自由边界使其在受到载荷时释放面内预压力,从而由凸起状态转变到相对平坦状态.然后在碳原子相互作用力的影响下使石墨烯在载荷的扰动下保持了一定的面外稳定性.正是因为这一点,石墨烯镜面屈曲现象载荷-挠度曲线与经典力学中跳跃失稳现象存在差异.之后随着载荷的进一步增长,碳原子间相互作用力不足以维持,横向载荷继续增大引发面外高度的增大.至于机械载荷和静电载荷作用下面外高度变化形式略有不同,这可能与载荷形式以及采样频率相关.

图4 CGMD计算得到石墨烯中心位置面外高度随时间的变化Fig.4.Curve of the out-of-plane heights in the center region of the graphene via the time calculated by CGMD.

综上所述,通过CGMD方法可有效还原STM实验中观测到的镜面屈曲现象,并对仿真结果进行记录提取,可以证明CGMD方法对于石墨烯镜面屈曲现象的分析具有有效性.

3 结果与讨论

3.1 石墨烯几何模型及计算设置

目前对于自支撑石墨烯热机镜面屈曲现象的研究,石墨烯膜的初始形貌并没有明确结论.在本文中,选择扇形截面的开口柱形石墨烯膜为模型,研究机械载荷、温度载荷及高跨比对石墨烯镜面屈曲现象的影响.参考其他仿真工作[36]以及弹性稳定性理论[37],截面高跨比λ=h/D,分别为2.5%,5%,7.5%,10%,20%和30%,截面形状如图5所示.

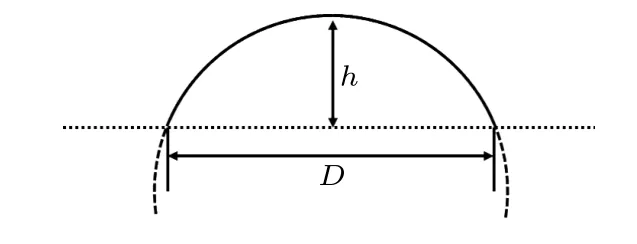
图5 石墨烯膜扇形截面示意图Fig.5.Diagram of the fan-shaped cross section of a graphene membrane.

截面参数确定之后,其他计算相关条件需要进一步确定.考虑到实验加载情况,即自支撑石墨烯膜在STM探针作用下同时受到静电载荷和热载荷的作用,所以机械载荷和热载荷对于石墨烯镜面屈曲的作用都有所研究.参考仿真计算中石墨烯的典型尺寸[22,36,38],对于粗粒化石墨烯模型,机械载荷施加在直径长度等于 1/10 跨度D的圆形中心位置,而温度载荷在整个环境中.石墨烯膜对应的跨度D=29.82 nm,长度L=28.78 nm.在开口柱形石墨烯膜两侧位置各有宽l0=0.5 nm的石墨烯带,将其固定作为边界条件.加载区域及边界条件设置如图6所示.机械载荷大小从1.086×10-3nN到7.599×10-3nN,间隔1.086×10-3nN,最后一组大小为1.086×10-2nN,共8组;温度载荷大小从3 K开始,之后从50 K增大到500 K,间隔50 K,共11组.具体参数如表2所列.

CGMD仿真计算通过开源代码LAMMPS[39]实现,可视化通过免费软件VMD[40]实现.原子间相互作用势选用2.1节中提及的表达式.时间步长1 fs,使用Nose-Hoover热浴法控温.施加机械载荷的情况下,在NVT系综中保持温度3 K施加相应载荷2 ns,系统稳定之后,再计算10 ns并获取数据;施加热载荷的情况与之类似,在NVT系综中保持设定温度2 ns作为弛豫,再计算10 ns并获取数据.

本文对石墨烯镜面屈曲的研究中,考虑了载荷大小、载荷形式以及高跨比的影响.对于不同高跨比的石墨烯模型分别施加机械载荷和热载荷,对比石墨烯膜稳定后截面轮廓图以及最大挠度-载荷曲线,研究分析各影响因素在热机镜面屈曲现象中起到的作用.为了更加直观且准确地比较计算结果,对计算结果进行无量纲化:=T/250,=f/(4.341×10-3),=w/(493.663).这里表示无量纲机械载荷,w¯ 表示无量纲石墨烯最大挠度.

3.2 扇形截面石墨烯镜面屈曲现象计算结果

1)机械载荷作用下高跨比和载荷大小对石墨烯镜面屈曲影响

图7所示为CGMD计算得到的不同高跨比石墨烯膜最大挠度随载荷变化曲线.对图7中各组曲线进行观察可以看出,挠度随载荷的变化趋势可以分为3种类型.对于λ=2.5%的小高跨比情况,石墨烯中心挠度随载荷的增大只产生小幅增长.对于λ=5%,7.5%,10%,20%的高跨比相对较大的情况,通过观察可以发现石墨烯中点面外挠度在随载荷发生一段缓慢增长后,突然产生长距离跳跃,即对应镜面屈曲现象.最后,对于λ=30%的大高跨比情况,石墨烯中心挠度基本随载荷的增加线性增长.将计算结果与STM实验结果(图1)进行对比可以发现,通过CGMD计算得到相似的面外高度变化趋势,说明石墨烯的高跨比也会对镜面屈曲现象产生重要影响.

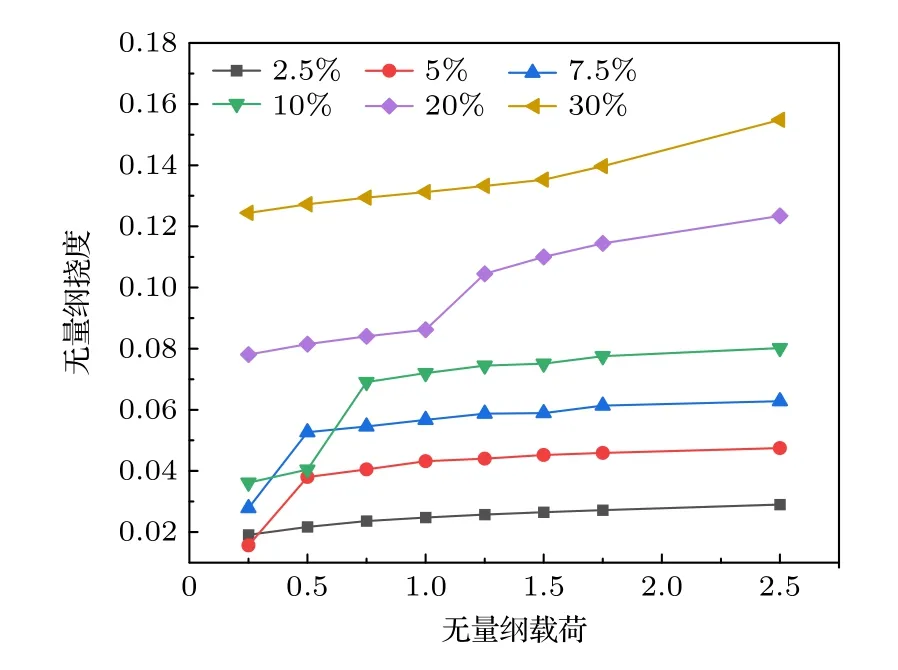
图7 扇形截面石墨烯膜的最大挠度随机械载荷的变化Fig.7.Maximum dimensionless deflections of the fanshaped cross-sections of graphene membranes versus the mechanical force.

四种典型高跨比石墨烯膜在不同机械载荷作用下对应的最大挠度截面轮廓图,如图8所示.通过截面轮廓可以更加直观地看到石墨烯在不同载荷作用下的变形情况.由图8可知,在λ=2.5%的情况下,石墨烯的稳定性相对较差,即使在小载荷作用下也会发生完全翻转现象.结合图7可以发现,高跨比较小的情况下石墨烯中心挠度随载荷的变化近似呈线性增长趋势,是处于已经发生翻转的状态,这一点与STM实验中小电流情况下石墨烯高度随偏压增大而增大但未发生翻转现象不同,这可能是两种计算形式中边界条件不同造成的.对于λ=5%,10%,20%的情况,石墨烯膜在较小载荷作用下维持相对稳定平坦的截面形状.载荷逐渐增大,直到石墨烯膜面外高度突然减小,发生镜面屈曲现象.值得注意的是,发生镜面屈曲现象对应的载荷随着高跨比的增大而逐渐增加,这与Timoshenko[37]提出的均匀受压圆拱两端铰支情况下高跨比与临界屈曲载荷变化趋势相同.在高跨比小于30%的情况下,临界屈曲载荷随着高跨比的增加而增大.对于同一高跨比的石墨烯膜来说,随着载荷的增大,挠度逐渐增大,直到超过临界载荷镜面屈曲现象产生,这同样符合屈曲理论.

图8 四种典型高跨比扇形截面石墨烯膜在不同机械载荷作用下,最大挠度截面轮廓图 (a) λ=2.5%;(b) λ=5%;(c) λ=10%;(d) λ=20%Fig.8.Cross-sectional profiles of maximum dimensionless deflections for the fan-shaped cross-sections of graphene membranes with the four typical depth-span ratio under different mechanical force: (a) λ=2.5%;(b) λ=5%;(c) λ=10%;(d) λ=20%.

2)热载荷作用下高跨比和载荷大小对石墨烯镜面屈曲影响

图9所示为CGMD计算得到的不同高跨比石墨烯膜最大挠度随温度的变化.对于λ=2.5%的小高跨比情况,石墨烯中心高度在温度的影响下几乎没有变化.对于高跨比稍大一些的情况,即λ=5%,在载荷增长的过程中,石墨烯中心高度变化存在两个阶段,在T¯=0—1.2 过程中,挠度随载荷的增大而增大;而在T¯=1.2—1.4 期间挠度几乎不变;在T¯＞1.4 之后石墨烯中心高度再次开始随温度的增加而增大.对于其他较大高跨比的石墨烯而言,挠度随温度载荷的增加只产生线性增长,甚至几乎没有变化.

图9 扇形截面石墨烯膜的最大挠度随温度载荷的变化Fig.9.Maximum dimensionless deflections of the fanshaped cross-sections of graphene membranes versus the temperature.

下面结合各种温度载荷作用下石墨烯的截面形状对温度和高跨比对镜面屈曲现象的影响进行进一步分析.四种典型高跨比石墨烯在不同温度载荷作用下对应的最大挠度截面轮廓图,如图10所示.图11所示为通过MD计算的在温度3000 K的环境下不同压缩率的圆形石墨烯膜中心高度随时间的变化[36].根据换算可以得到图中压缩率ε=0.13%,0.67%,0.78%分别对应于高跨比λ=2.3%,5.3%,5.7%.

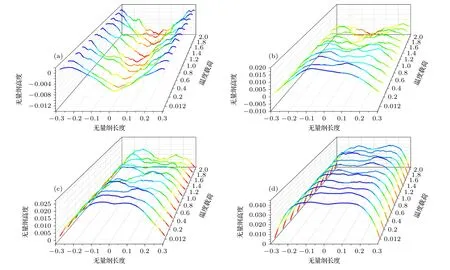
图10 四种典型高跨比扇形截面石墨烯膜在不同温度载荷作用下,最大挠度截面轮廓图 (a) λ=2.5%;(b) λ=5%;(c) λ=10%;(d) λ=20%Fig.10.Cross-sectional profiles of maximum dimensionless deflections for the fan-shaped cross-sections of graphene membranes with the four typical depth-span ratio at different temperature: (a) λ=2.5%;(b) λ=5%;(c) λ=10%;(d) λ=20%.

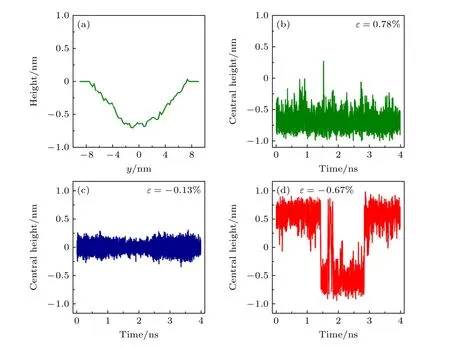
图11 3000 K下应变对波纹的动态影响[36]Fig.11.Role of strain on ripple dynamics at 3000 K[36].

由图10可知,在λ=2.5%的小跨高比情况下,无论温度载荷的大小,石墨烯始终处于可翻转状态.这种围绕初始高度反复进行曲率翻转的行为与相近高跨比(ε=0.13%)下石墨烯在温度载荷作用下的行为相近.对于λ=5%情况,温度载荷的增加使石墨烯中心高度降低,并在T¯=2 时发生完全翻转.由此可知,CGMD计算得到的石墨烯曲率翻转现象与ε=0.67%石墨烯在高温下发生的翻转行为有所对应.对于λ=10%,20%的较大高跨比情况,石墨烯构型在温度载荷的作用下基本保证稳定状态,没有产生明显的翻转现象,同样与ε=0.78%较大压缩率下石墨烯的中心高度变化相近.通过将CGMD与MD对不同高跨比石墨烯施加温度载荷的计算结果进行对比后发现,两者得到的石墨烯变形行为相近.

一般情况下,温度的升高有助于石墨烯发生镜面屈曲现象.升高温度即原子运动加剧的宏观表征.但由于原子间相互作用,碳原子并不会向随机方向运动,而是在周围原子的牵引下受到一定约束的运动.运动速度的加快以及运动方向上一定的约束综合导致升高温度有助于镜面屈曲现象的发生.与此同时,石墨烯高跨比也会对镜面屈曲现象的产生造成影响.对于λ=2.5%的情况,即使温度较低也会使石墨烯完全翻转,且最大挠度随着温度的升高缓慢增加.在λ=5%时,石墨烯中心高度随温度的升高而逐渐降低,当温度足够高达到T¯=2的情况下,石墨烯发生完全翻转.对于λ进一步增大的情况,即使温度升高也只能观察到石墨烯膜面外高度下降,突跳现象不会出现.

4 结论

本文采用CGMD方法,对扇形截面不同高跨比石墨烯膜分别施加机械载荷和温度载荷,研究高跨比、载荷大小以及载荷类型对于镜面屈曲现象的影响.首先通过CGMD仿真计算结果与STM实验观测结果对比可知,CGMD方法可以有效地对镜面屈曲现象进行计算分析,证明其有效性.

随后在对各个影响因素的分析中可以发现,机械载荷作用下,在小高跨比λ=2.5%的情况下,即使在小载荷作用下也会发生镜面屈曲现象.对于较大高跨比λ=5%,10%,20%的情况,在小载荷作用下石墨烯可能产生局部坍塌,当载荷增大到临界值时,石墨烯面外高度突然发生长距离跳跃,即产生镜面屈曲现象.由此可见,在机械载荷作用下,对于高跨比各异的石墨烯都能够产生镜面屈曲现象,且对应的临界载荷随着高跨比的增加而增大.

对于温度载荷来说,在小高跨比λ=2.5%的情况下,无论温度载荷大小,石墨烯始终处于可翻转状态.对于λ=5%的情况,在T¯=2 的较高温度作用下能够发生完全翻转现象.对于更大高跨比的石墨烯来说,随着温度的升高只观察到中心高度的下降,完全翻转的现象并没出现.分析可知,高跨比对温度载荷下石墨烯的高度变化影响较大,小高跨比的情况下更容易发生翻转,对于大高跨比的情况,温度载荷的增加使中心高度的变化增大,可能导致翻转情况的发生,但当高跨比进一步上升时,温度的升高带来中心高度的下降,但是不会导致完全翻转的发生.

在载荷类型、载荷大小以及高跨比之外,还存在截面形状、边界条件等更多条件可能对石墨烯镜面屈曲现象产生影响,之后的工作可以展开对更多因素的分析工作.通过对石墨烯膜镜面屈曲现象更加全面细致的研究,清楚各因素对其的影响作用,有助于基于石墨烯膜的能量收集系统的设计和优化工作.