基于X射线荧光光谱的温稠密物质电子结构密度效应研究*
张志宇 赵阳 青波 张继彦 马建毅 林成亮 杨国洪韦敏习 熊刚 吕敏 黄成武 朱托 宋天明 赵妍张玉雪 张璐 李丽灵 杜华冰 车兴森黎宇坤 詹夏宇 杨家敏†
1) (中国工程物理研究院激光聚变研究中心,绵阳 621900)
2) (四川大学原子与分子物理研究所,成都 610065)
3) (北京应用物理与计算数学研究所,北京 100088)
1 引言
温稠密物质(warm dense matter,WDM)是介于冷凝聚态物质和高温等离子体之间的一种过渡态物理体系,温度在1—100 eV、密度达到0.1—10倍固体密度,具有强耦合和部分简并特性,广泛存在于自然天体中,亦是惯性约束聚变等极端物理过程所必须经历的重要物质状态[1,2].举例来说,在激光间接驱动惯性约束聚变[3]中,壳层、燃料都会被压缩到温热稠密状态,材料在温稠密状态下的不透明度、状态方程等对内爆性能影响很大[4-7].
相较于孤立原子,经历加热和压缩的稠密物质,受环境中自由电子和离子的屏蔽,其电子波函数发生严重畸变,出现能级展宽、移动以及压致电离等.电子结构的变化会改变稠密物质中的辐射与流体物理性质,影响辐射能的输运和交换、材料的辐射不透明度以及电离平衡等.鉴于稠密物质微观电子结构的复杂性,理想等离子体和凝聚态物质模型都不能对其进行准确描述,而基于第一性原理的理论研究也非常复杂[8-13].即便是对温度较高的热稠密物质(几百eV),束缚电子几乎被完全电离,理论方面仍不能完全描述其电子结构行为: Ciricosta等[14]在LCLS (linac coherent light source)装置上的实验结果与EK (Ecker-Kröll)电离势降低模型结果符合较好,但与SP (Steeart-Pyatt)电离势降低模型结果符合不好;Hoarty等[15]在Orion装置上的实验结果则刚好相反,与SP电离势降低模型结果符合较好,但与EK电离势降低模型结果符合不好.对于温度相对较低的温稠密物质(1—100 eV),原子核周围还有较多的束缚电子,相互作用体系及理论描述更加复杂.
随着高功率强激光等技术的发展,温稠密物质实验研究也逐步开展起来.在温稠密物质产生方面,基于强激光的等容加热或冲击加载是开展温稠密物质实验研究的主要加载手段之一[16-20].X射线光谱是研究温稠密物质电子结构改变及辐射光谱特征的重要手段,主要包括两种途径: 吸收光谱法和发射光谱法.自Bradley等[21]的研究开始,利用X射线吸收边光谱诊断温稠密物质K吸收边的展宽和移动已经开展不少研究[22-26],观测到温稠密物质K吸收边随状态的变化,且实验结果与理论结果的差异随密度升高而变大.通过考虑核电子的影响,Mazevet等[9,24]已经能够在较低密度范围内(Al,< 5 g/cm3)获得与实验结果符合较好的理论结果,但是在更高密度情况下,理论结果与实验结果差距较大.张珅等[11]通过更好地考虑K壳层及L壳层电子,可以在更高密度范围内与实验结果符合.以上利用吸收边光谱所获得的结果主要研究了温稠密物质吸收边随状态改变而发生的变化,但是对束缚电子能级结构的变化无法直接研究.
通过束缚-束缚跃迁发射的keV能区X射线光谱,可用于研究束缚电子能级结构[27].但是由于温稠密物质的温度较低,仅通过电子碰撞激发机制很难产生足够的内壳层空穴,因此实验中难以测量到keV能区的束缚-束缚跃迁X射线发射光谱.为此,不妨通过外加X光泵浦源移除K壳层电子并产生空穴,外壳层电子有一定概率通过跃迁填补空穴并发射荧光,借助X射线荧光光谱可研究温稠密物质的束缚电子能级结构.不过,即使利用外源泵浦,能够产生的发射谱线强度仍然较弱,因此开展温稠密物质X射线荧光光谱实验研究需要克服弱信号测量的问题.鉴于对实验加载能力与诊断条件要求非常苛刻,温稠密物质的荧光光谱实验研究开展得比较少.Hansen等[28,29]在Sandia的Z装置利用内爆加载和泵浦的方式获得了掺杂在Be壳层中Fe的 Kα,Kβ荧光谱线并观测到谱线的红移,但实验是将Fe掺杂在Be中,其环境主要是低原子序数的Be离子及电子.Jiang等[30]利用激光直接驱动斜波压缩产生了约2倍固体密度、温度小于1 eV 的Co,利用超热电子泵浦Co的荧光,诊断到其 Kβ谱线约2.6 eV的红移,与密度泛函方法计算结果一致,但与不同碰撞辐射模型(考虑SP和EK电离势降低)的理论模拟差异随压缩度增加逐渐增大,因此开展更多材料及状态下实验与理论的对比研究需求非常迫切.
本文介绍了基于激光间接驱动开展的荧光光谱实验,获得了压缩状态Ti样品的X射线荧光光谱并观测到谱线随状态的变化,研究了密度效应对温稠密物质电子结构的影响,通过与计算结果的比较校验了两种理论方法.
2 实验方法及排布
实验在万焦耳激光装置上开展,包括荧光光谱测量和样品处辐射源测量两部分内容,实验示意图如图1所示.如图1(a)所示,在荧光光谱测量实验中,4路激光(4 × 800 J,1 ns,3倍频)从上注入口(Φ 800 μm)注入用于加载的半腔(哑铃型黑腔,材料为Au)转换为X射线,激光的焦平面在上注入口位置,光斑大小为Φ 500 μm.基于特殊的黑腔构型设计,放置于半腔尾部的CH包裹Ti样品(CH/Ti/CH)不会受到激光打靶点的散射激光以及高能X射线的影响,样品处的辐射场更接近Planck辐射场,会在样品中形成辐射冲击加载产生大于固体密度且温度较低的样品.4路激光(4×240 J,300 ps,3倍频)从下注入口(Φ 800 μm)注入到V腔,产生V的 Heα(5.21 keV)以及Lyα(5.44 keV)等特征X 射线作为泵浦源,激光的焦平面在下注入口位置,光斑大小为Φ 500 μm.泵浦源会泵浦Ti样品的K壳层电子(电离能约为4.97 keV),有一定概率是外壳层(L,M)电子通过跃迁填补K 壳层空穴并发射荧光(Kα,Kβ).Ti样品荧光光谱的测量是采用晶体谱仪实现的,Ti样品发射的光谱通过晶体时,由于布拉格衍射效应,不同能量的X 射线会在不同的角度反射从而被色散,因此记录设备上的一维空间分辨会转换为谱分辨.本次实验采用的晶体为TAM平面晶体,其2d值为0.878 nm.由于泵浦效率以及荧光发射效率的影响,荧光信号是一个弱信号,为了提升信号强度,实验中采用灵敏度更高的真空X光CCD作为晶体谱仪的记录设备,解决了其在真空靶室中使用时的电磁屏蔽问题.实验中通过调控加载激光与泵浦激光的延时(各路激光之间的同步或延时精度好于30 ps),获得了不同状态Ti样品的荧光光谱.
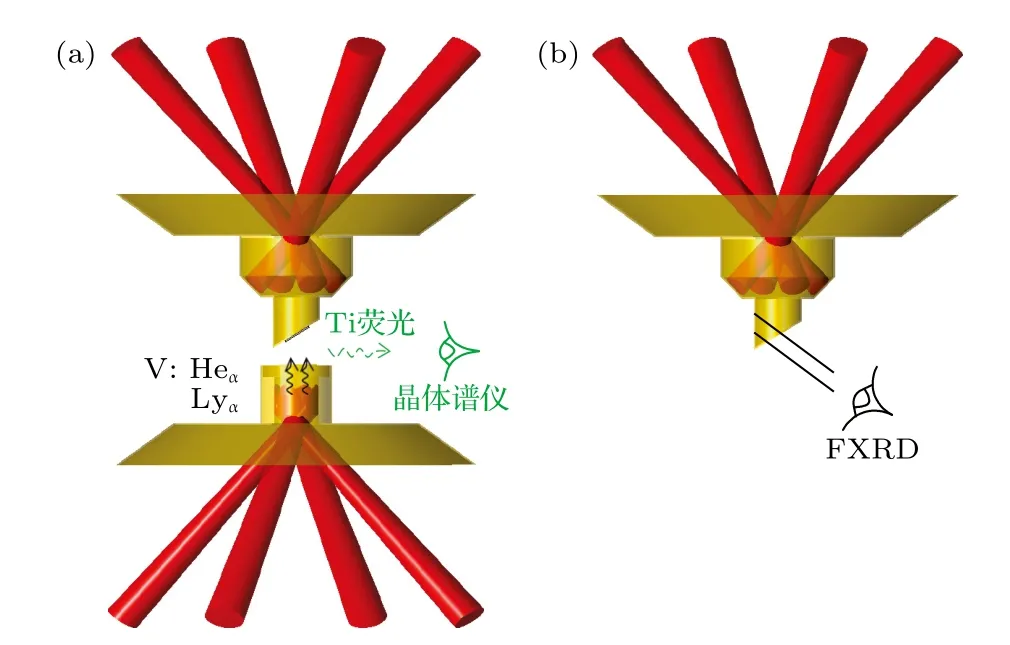
图1 温稠密Ti的荧光光谱实验示意图 (a)荧光光谱测量;(b)样品处辐射源测量Fig.1.Schematic of the X-ray fluorescence spectrum experiment of warm dense Ti: (a) Measurement of the fluorescence spectrum;(b) measurement of the incident flux of the sample.
为了更好地开展样品状态的模拟及分析,需要知道样品处加载辐射源的分布.但是,实验中无法直接诊断该加载源,因此采用间接测量的方式.Lindl[2]提出可以通过测量Au的再发射辐射温度TR来反推入射到Au上的辐射温度TI:
其中,T和τ的单位分别为100 eV和ns.
如图1(b)所示,在辐射源测量实验中,4路激光(4 × 800 J,1 ns,3倍频)从上注入口注入半腔,半腔尾部无样品,采用平响应X射线衍射仪(XRD)从半腔尾部的诊断孔诊断腔壁的再发射辐射流,进而给出诊断孔(样品)处的辐射源.图2(a)给出了实验中诊断到的辐射温度分布TR以及利用Lindl的方法给出的入射到该区域的辐射温度分布TI,入射辐射温度的峰值约为90 eV.由于该位置与样品位置很接近,样品处的入射辐射温度与该结果比较接近.进而,利用辐射流体程序MULTI-1D[31]可以模拟该辐射源加载下Ti中心样品的状态演化过程,结果如图2(b) 所示,冲击到达Ti样品的时刻约为1.5 ns,压缩状态维持约400 ps,其密度为7.2—9.2 g/cm3,温度在1.6—2.4 eV.
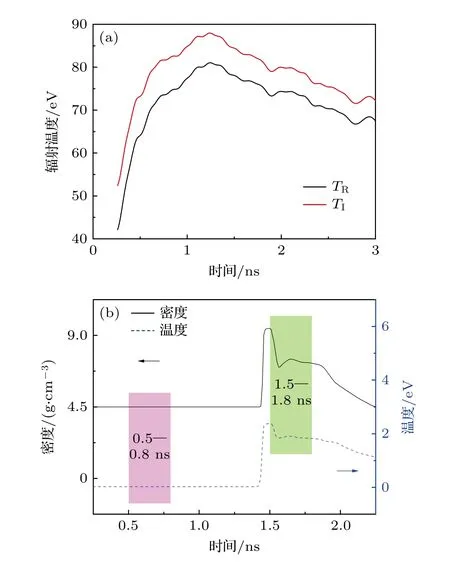
图2 (a)样品处再发射流及入流;(b) Ti样品的密度温度演化过程模拟结果Fig.2.(a) Reemission flux and incident flux of gold at the hohlraum center;(b) the simulated density and temperature evolution of Ti sample.
3 实验结果及讨论
综合考虑样品压缩状态维持时间和信号强度,实验中设置泵浦激光的脉宽为300 ps,通过调控泵浦激光相对加载激光的延时,获得了不同加载时间(0.5—0.8 ns,1.5—1.8 ns)样品的荧光发射光谱,如图3(a)所示.为了确认诊断到的光谱是Ti样品的荧光光谱,实验中还开展了本底测量,将图1(a)中的样品去除并保持4路加载激光和4路泵浦激光注入,晶体谱仪所诊断的图像中无任何信号,因此可以确认图3(a)中的信号为Ti 的 Kα以及 Kβ荧光谱线.对于诊断窗口为0.5—0.8 ns的实验结果,从图2(b)可以看出,此时样品尚未被加载,谱仪诊断到的是冷样品的荧光光谱.对于诊断窗口为1.5—1.8 ns的实验结果,根据图2(b)中样品的状态演化过程,谱仪诊断到的是压缩样品(7.2—9.2 g/cm3,1.6—2.4 eV)的荧光光谱.

图3 不同状态Ti样品的荧光光谱 (a)原始图像;(b)解谱结果Fig.3.The X-ray fluorescence spectrum of Ti samples with different state: (a) Original images;(b) spectral results.
冷Ti样品的 Kα和Kβ的能量已知,结合布拉格衍射公式,即可对冷Ti样品的荧光光谱图像解谱.对于压缩样品,由于内壳层电子受环境效应影响较小,相对于 Kβ谱线,Kα谱线的变化很小,解谱时设定Ti的 Kα谱线不变,结合整套晶体谱仪在实验期间处于完全静止状态,即可解谱.解谱结果如图3(b)所示,Ti的 Kα荧光谱线的计数强度约为1000,其 Kβ荧光谱线的计数强度约为100,二者的强度相差约一个数量级,与理论中二者的荧光效率一致.在设定Ti的 Kα荧光谱线没有变化的前提下,压缩状态下Ti 的 Kβ荧光谱线红移约2 eV,即加载样品的Kβ和Kα的能量差相对于冷样品的变小约 2 eV.这个变化不是发次间的谱仪位置和样品位置的扰动引起的,晶体谱仪的记录设备为真空X光CCD,整个谱仪的位置在不同发次中不会变化;样品在不同发次中的位置可能发生变化,但是样品上下移动时 Kα和Kβ在记录介质上记录是平移,能量差几乎无变化,样品前后移动时,会发生变化但变化量很小,以放置样品时的最大偏差50 μm为例,的变化约为0.05 eV,远小于2 eV.因此诊断到的荧光谱线的移动是因为加载状态下温稠密物质的电子结构发生变化导致的,其变化趋势与文献[30]结果一致.
为了进一步研究密度效应对荧光光谱的影响,采用了两种理论方法开展温稠密Ti样品K壳层荧光谱线的计算.
第一种方法是有限温度相对论密度泛函方法(FTRDFT),是在Beijing Density Functional程序包[32]的基础上发展的有限温度相对论算法,计算时采用BP86泛函和Triple-Zeta Slater 数值基.
对于有限温度密度泛函方法的算法实现,其单粒子运动方程为
其中,
这里,m为电子质量,n为电子密度,r为位置坐标,ψ为轨道波函数,ν(r) 为核电势,Ω为交换相关泛函,β=1/(kT),ε为轨道能量,μ为化学势.
在相对论情况下,动能算符采用四分量相对论形式.计算时采用 Ti15团簇,中心原子被两层Ti原子包围,构成压力环境,然后考察中心原子的光谱变化行为.
第二种方法是“two-step Hartree-Fock-Slater”(TSHFS)理论模型[33,34].
TSHFS理论模型的第1步是求解基于平均原子模型的Hartree-Fock-Slater方程以获取平均组态中电子的轨道能量.对于给定的量子态 |al〉,其波函数ual(r) 满足如下形式的径向薛定谔方程:
其中势能的形式由Hartree-Fock-Slater势能给出,其特点是在Wigner-Seitz球外的势能为常数.这里l是角量子数,V是相互作用势能,ε是对应量子态 |al〉的能量.在求得不同l分波的波函数和轨道能量后就可以据此构造不同组态的占据概率,进而可以得到价态为Q的离子丰度.
同一价态不同组态之间跃迁的能量则由第2步给出,仍然是一个求解Hartree-Fock-Slater方程的过程.第2步与第1步的差别在于,此时束缚轨道上的电子占据数不再是平均原子中的分数占据,而是整数占据(占据为1,未占据则为0),更符合真实的物理体系.针对给定组态计算出其束缚轨道能量后,不同谱线的跃迁能量就可以定义为相应轨道之差.

图4 不同状态Ti样品 相对于冷样品的变化Fig.4.Changes of of Ti with different density and temperature relative to cold samples.
4 结论
通过发展基于激光间接驱动的温稠密物质X射线荧光光谱实验方法,研究了密度效应对温稠密物质束缚能级电子结构的影响.基于特殊构型黑腔加载产生最高约2倍固体密度、2 eV的温稠密物质,采用TAM晶体谱仪配真空X光CCD获得冷样品以及压缩样品的荧光光谱,观测到荧光谱线在压缩状态下相对于冷样品有约2 eV的红移.通过与理论结果的比较表明,FTRDFT高估了密度效应对 Kβ谱线移动的影响,而TSHFS低估了密度效应的影响.后续需继续精密化X射线荧光光谱实验研究方法并获得更多状态下Ti 样品的荧光光谱,在更宽的状态区间内校验温稠密物质理论研究方法.

