基于TFDR 波形时域包络线的电缆故障定位技术

吴吉，唐作鑫，彭向阳，王昱皓，于是乎，周凯

（1. 广东电网有限责任公司电力科学研究院，广州 510080；2. 四川大学电气工程学院，成都 610065）

0 引言

电缆通常会因敷设环境和制作工艺问题在局部产生绝缘缺陷，随着运行时间的增长，电缆局部绝缘会进一步下降，直至发生电缆故障，从而造成停电事故。主流的检测方法如绝缘电阻测试法［1］、介质损耗因数（tanδ）测试法［2］以及最新的极化-去极化电流 （polarization depolarization current，PDC）［3］测试法可以获得表征电缆绝缘状态的参数，实现对电缆整体绝缘性能的判断，但是此类方法得到的参数所反映的是电缆整体绝缘状态，无法对引起电缆整体绝缘下降的局部缺陷/故障进行定位诊断。为了能够准确定位电缆局部缺陷/故障、有效评估局部缺陷/故障的绝缘情况，已有许多国内外学者展开了大量研究，传统的电缆缺陷定位技术主要有直流电桥法［4］、局部放电法［5］与行波法［6］3 种，这些方法原理简单，在实际现场中得到了较为广泛的应用，但是存在定位误差大、缺陷识别能力低、测试效果受噪声影响较大等问题，无法保证复杂现场测试条件下对精度的要求。文献［7］分析了直流电阻法高压电缆外护套故障测距误差产生的原因，给出了减小故障测距误差的改进措施，但是该方法只应用于高压电缆，且受噪声影响较大。文献［8］归纳了针对海缆监测的常用技术，总结出海缆监测技术的关键技术的发展现状，但是这些方法无法对海缆具体缺陷进行定位。文献［9］介绍了频域响应法的基本原理，梳理了基于宽频输入阻抗谱和基于首端反射系数谱的频域响应法及其定位改进算法的研究进展，但是实际测试时往往通过鳄鱼夹将仪器与电缆首端进行连接，使得信号注入效率偏低。

时频域反射法（time-frequency domain reflectometry，TFDR）本质也属于行波反射法，该方法通过向电缆首端注入具有高斯包络的线性可调频信号（Linear frequency modulation，LFM），通过计算入反射信号的时频域相似性得到信号的时频域相关程度用以确定缺陷或末端位置，实现对局部缺陷的定位［10-11］。该方法相较于时域反射法（time domain reflectometry，TDR），基本原理是通过向被测试电缆首端注入高斯脉冲信号，通过示波器观察其时域上的反射波形记录时间延迟，最后根据电缆中电磁波的传播速度进行计算，对电缆局部缺陷处的反射位置进行测试等，其最大的特点是入射参考信号的不同，该信号为时限带限，且在时域上具有高斯包络特性，可任意调节参数的非平稳信号。对其进行时频域分析可得到该信号的时变频谱特性，同时可获得任意时频条件下的信号能量强度。本文提出一种基于波形时域包络线的定位技术，提高了TFDR的缺陷定位精准度；同时研究发现结合时域波形变化情况，可对缺陷类型进行判断；最后分别对50 m及500 m 长的电力电缆进行实际测试，证明了包络线方法的有效性。

1 TFDR定位原理

1.1 电缆分布参数模型及传递函数

由传输线理论可知［12-13］，为了能够正确描述信号在电缆中能量传递特性，在高频条件下须将电缆等效为无数个图1 所示的微分段分布参数等效电路的级联。

图中：R0、G0、C0、L0分别为电缆单位长度Δx的电阻、电导、电容、电感。该分布式参数模型的各参数可分别计算［14-15］为：

式中：ω=2πf为角频率；f为信号的频率；rc为缆心的半径；rs为金属屏蔽层的半径；ρc为缆心的电阻率；ρs为金属屏蔽层的电阻率；μ0为真空磁导率；σ为交联聚乙烯的电导率；ε为交联聚乙烯的介电常数。

若对不含缺陷电缆注入稳态行波信号，行波传播过程如图2所示。

图2 完好电力电缆中行波反射示意图Fig. 2 Schematic diagram of traveling wave reflection in intact power cable

电缆首端反射系数如式（5）所示。

式中：Г（ω）为电缆首端反射系数；ZL为电缆末端负载的阻抗；Z0(ω)为电缆的特性阻抗；γ（ω）为电缆的传播特性曲线；l为被测电缆长度。其中：

当电缆发生局部缺陷时，特性阻抗将发生改变，因而首端阻抗也会发生改变［16］。

建立长度为l的电缆仿真模型，对距离电缆首端x=la至x=lb处局部缺陷段展开分析，含缺陷电缆模型如图3所示。

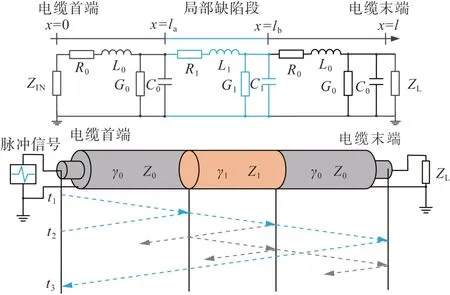
图3 缺陷电缆行波反射示意图Fig. 3 Schematic diagram of traveling wave reflection of defective cable

图3 中γ0为正常情况下电缆的传播常数；γ1为局部缺陷段的传播常数；Z0和Zl分别为正常电缆及局部缺陷段的特性阻抗。当电缆局部因存在中间接头、受潮、铜带缺失等情况时，会导致该部分的特性阻抗及传播常数等与正常电缆有所不同，行波在传播至局部缺陷段时，因其阻抗突变会产生折反射现象，此时将电缆分为三段，首端x=0 至x=la为第一段，局部缺陷段为第二段，x=lb至x=l为第三段。

电缆第三段首端的反射系数Гlb以及x=lb处的输入阻抗Zlb为：

局部缺陷段首端的反射系数Гla以及x=la处的输入阻抗Zla为：

电缆首端的反射系数Г0以及首端输入阻抗ZIN为：

根据公式推导可得，电缆的首端反射系数或输入阻抗可以很好地反映局部阻抗不匹配区段的位置信息，因此本文选择电缆首端反射系数Г0作为电缆最终定位及分析的传递函数H（ω）进行诊断及分析。

1.2 时频域反射法

TFDR 利用一个高斯包络的线性可调信号作为入射信号。信号s（t）表示如下［17］。

式中：α为参考信号的宽度，即信号的持续时间，α与脉宽呈反比关系，即α越大脉宽越窄；β为信号的频率带宽，与频带宽度呈线性关系，即β越大频带越宽，可视为时频分布的斜率；ω0为中心角频率，与中心频率f0的关系为ω0=2πf0；t0为可调频参考信号的中心时间。正是因为该信号的可调性，可根据实际被测电缆的长度等信息进行调整，以达到最佳的定位测试效果。

当中心频率f0设定为200 MHz，频带宽度bs设定为100 MHz，信号的脉宽Ts设定为30 ns，时间中心t0设定为50 ns时，通过上述计算可得到参考信号相应的参数α=3.125×1016，β=2.5×1016。其时域波形如图4所示。

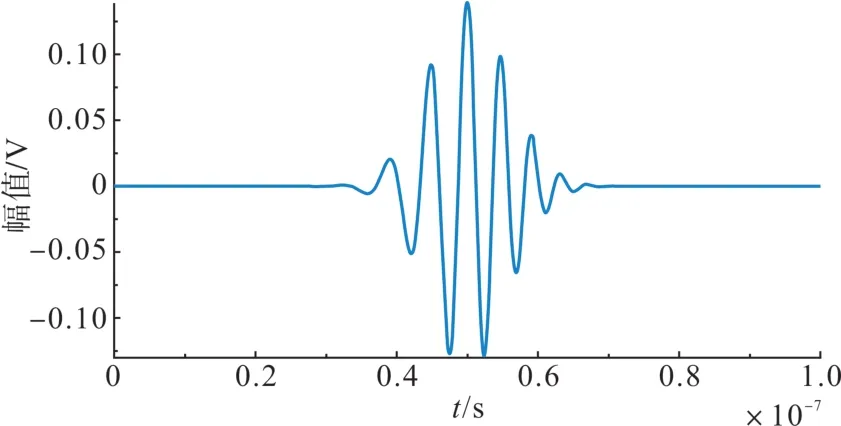
图4 高斯包络的线性调频信号Fig. 4 Chirp signal with Gaussian envelope

当被测试电缆长度较短时，此时应将参考信号的中心频率f0设置得较高，避免信号在传播过程中的波形混叠，从而保证此时能够完整地对缺陷进行分辨；同时当电缆长度较长时，由于信号高频分量在电力电缆中传播时的衰减较大［18］，若选用中心频率较高的参考信号会导致末端反射的能量极低，若此时缺陷距离测试端较远，极有可能因为能量损耗而导致无法探测。因此针对长距离电缆，为减少信号高频损失的影响需要选择较低的中心频率，以保证能够对整根电缆进行探测。

中心频率和信号脉宽需要满足一定的值时，才可以使得参考信号波形满足较好的时域分辨细节。同时频率带宽不应过大，否则会导致波形的畸变。总而言之，TFDR 的参考信号可根据被测试电缆的情况进行灵活调整，具有较高的适应性，在实际电缆局部缺陷定位诊断中具有较好的效果，相比于传统定位方法有明显的优势。

2 基于时域包络线的定位技术

2.1 波形时域包络线定位技术

本文根据参考信号的特性提出利用其高斯包络的性质从时域上利用信号的包络线进行定位。参考信号的包络线可较好地对整个时域的信号能量进行反应，且波形时域包络线不会因为波形的畸变而变化。

电缆的局部电容变化通常作为缺陷的一种表征形式［16］，现根据第2节电缆传输线模型，建立25 m以及500 m 长的10 kV XLPE 电力电缆仿真模型，分别在距离电缆首端10 m 以及200 m 处设置局部电容减小为本体电容0.9 倍的缺陷段，即Cp=0.9Cn。其中Cp为局部缺陷段电容，Cn为电缆本体电容，缺陷段长度设置为0.05 m，电缆相关参数选择如表1所示。

表1 电缆仿真模型的参数设置Tab.1 Parameter settings of the cable simulation model

其中，针对短电缆样本的参考信号s（t）参数选择为：信号脉宽Ts=4×10-9s，频带宽度bs=20 MHz，中心频率f0=200 MHz；长电缆样本的参数选择为：信号脉宽Ts=8×10-8s，频带宽度bs=1 MHz，中心频率f0=10 MHz。

为了得到仿真电缆模型中反射信号，本文利用电力电缆的传递函数即电缆的首端反射系数进行计算。首先通过对输入信号s（t）求取快速傅里叶变换并与电力电缆的传递函数H（ω）进行卷积，再对卷积过后的结果通过快速傅里叶反变换进行计算，以此得到反射信号r（t）的时域波形。具体计算公式如式11所示。

式中：FFT快速傅里叶变换；IFFT为快速傅里叶反变换。图5（a）所示为短电缆模型的时域波形反射结果，可见其缺陷处的反射较为微弱，若仅通过肉眼观察较难识别，而图5（b）所示长电缆模型的时域波形结果可以看出，缺陷处反射通过肉眼观察几乎已经完全不可见，同时相比25 m 短电缆模型，500 m的长电缆模型入射参考信号在电缆中传播时受到衰减因素的影响，其末端反射幅值明显降低。

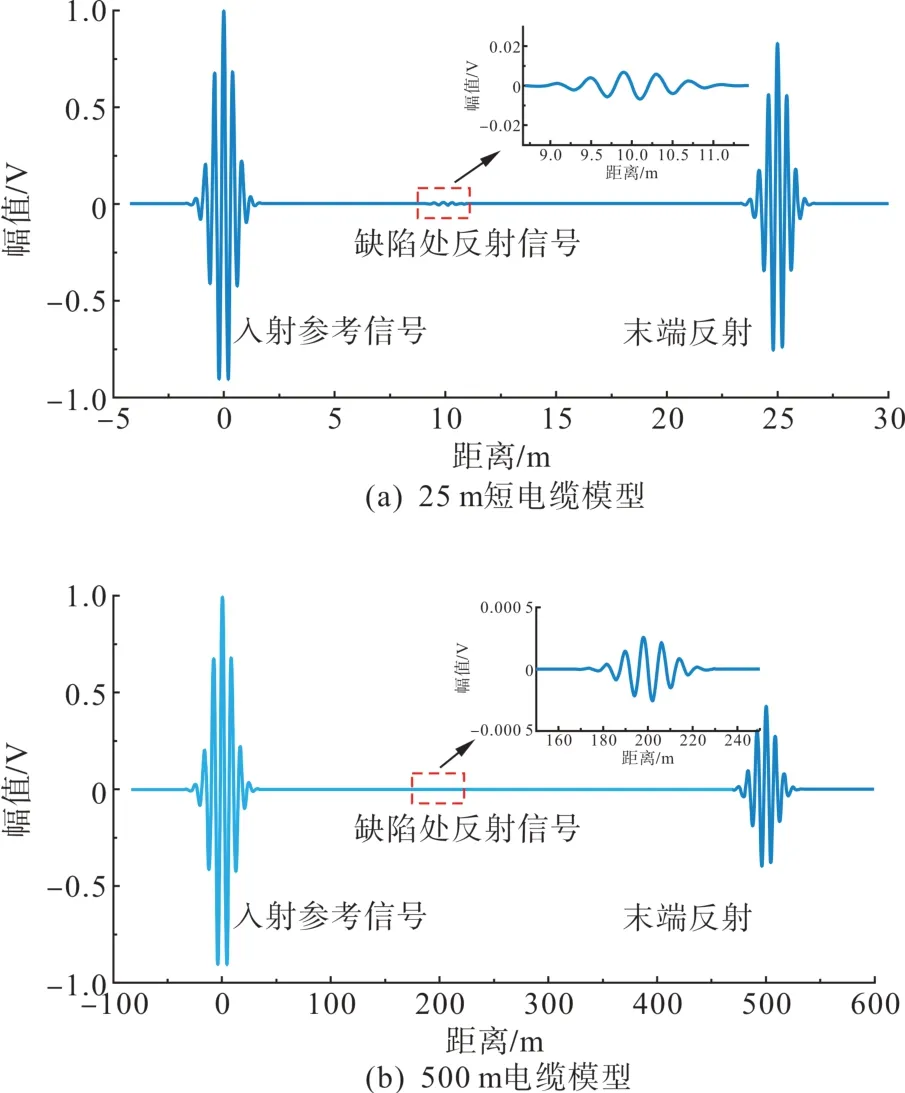
图5 不同长度电缆模型的入反射信号时域波形Fig. 5 Time domain waveforms of incoming and reflected signals for different length cable models

由此可见通过时域波形直接进行定位诊断具有较大的局限性，当电缆较长时信号能量衰减严重，局部缺陷处反射幅值极低，无法直接通过时域波形观察进行定位。但值得一提的是，由于本文选择的参考信号为具有高斯包络的线性可调频信号，为此，可通过参考信号的特性求取波形时域上的包络线进一步处理从而实现最终的缺陷定位。由于长电缆局部缺陷反射更弱，25 m短电缆的局部缺陷仍可通过肉眼观察，因此为验证该方法的有效性，下面针对500 m长的电缆模型进行处理。

利用傅里叶变换获取反射信号r（t）后，记入反射叠加信号为g（t）=s（t）+r（t），对叠加信号g（t）求取希尔伯特变换［19］，并求取其模值即可获取该叠加信号的包络线eng（t）。

式中：Hilbert（·）为希尔伯特变换；abs（·）为取模。求得500 m 电缆模型入反射叠加信号的时域包络结果如图6所示。

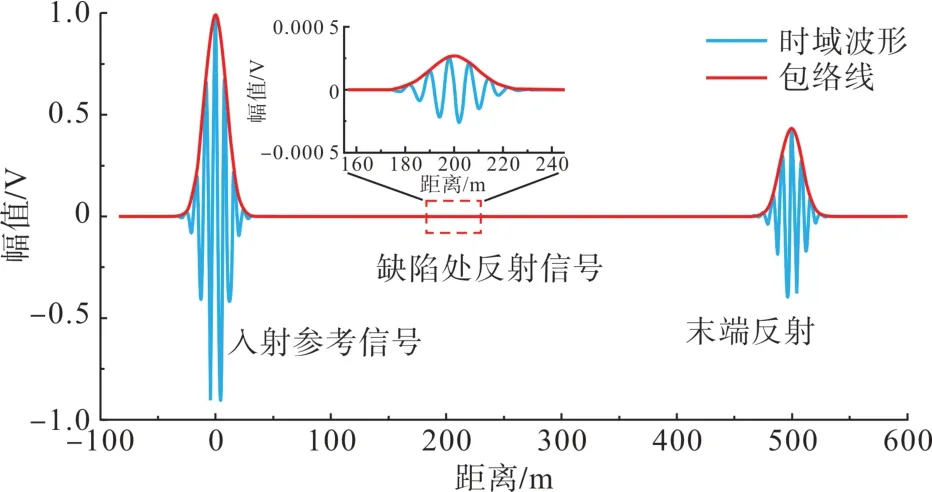
图6 叠加信号的时域包络线Fig. 6 Time-domain envelope of the superimposed signals

可见参考信号具有很好的高斯包络特性，为定位结果更为直观对所求得的包络线采取对数坐标显示，并对最终结果采取归一化处理，得到的定位结果如图7所示。

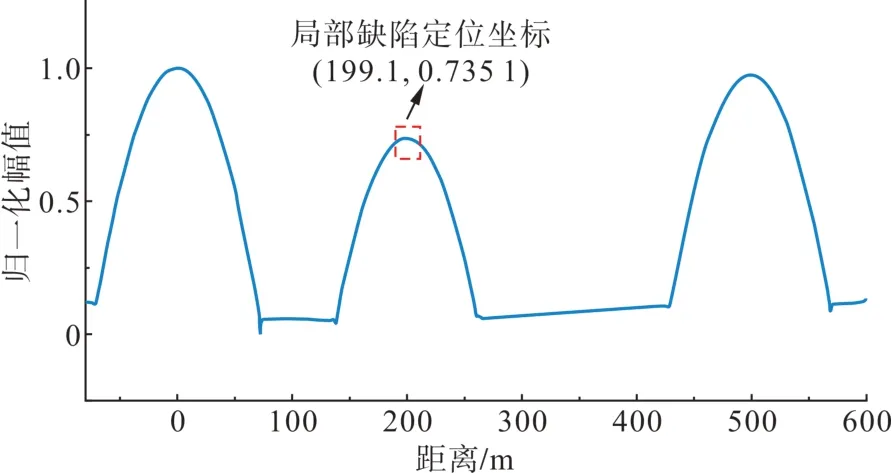
图7 500 m电缆包络线定位结果Fig. 7 Locating results of 500 m cable envelope

为更好地显示缺陷处时域波形，对比分析不同缺陷类型的时域波形情况，将上述500 m 电缆模型的200 m 区域的局部缺陷段增大为1 m。并利用单一高斯脉冲（TDR）对模型进行仿真实验，分别对局部电容增大1.05 倍以及局部电容减小为本体电容0.9 倍的情况进行分析。为便于观察TDR 定位结果，本文将TDR 幅值作归一化处理，得到更为直观的TDR定位结果对比，如图8所示。

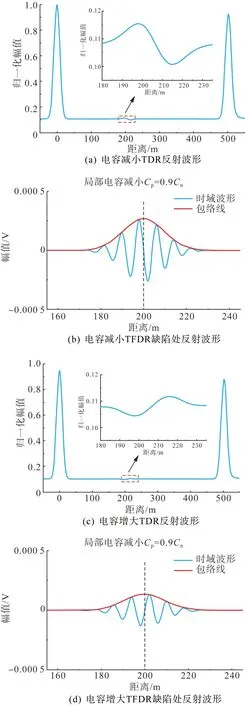
图8 TDR波形与TFDR波形对比Fig. 6 Time-domain envelope of the superimposed signals

可以发现，TFDR 采用的参考信号同样具备一定的缺陷类型识别能力，与TDR 类似，可根据包络线轴对称线左右两侧的波峰波谷进行判断。且当缺陷更为严重时缺陷处的时域反射波形幅值也会相应增大。

当局部电容减小时，如图8（b）所示，局部电容为本体电容0.9倍缺陷处波形与TDR 表征类似，在包络线轴对称线左侧出现正峰，右侧出现负峰，即“先正后负”。

当局部电容增大时，如图8（d）所示，局部电容为本体电容1.05 倍缺陷处波形与TDR 表征同样类似，在包络线轴对称线左侧出现负峰，右侧出现正峰，即“先负后正”。

从理论上分析，当电缆局部电容减小时，由于阻抗与电容呈反比关系，即当电缆局部电容减小，其局部阻抗会增大，因此便会产生正反射，而当局部电容减小时则相反，会发生负反射。因此波形在进入局部电容减小的缺陷段时会发生“先正后负”的反射。反之同理。

为了验证包络线定位方法定位的准确性，本文在上述500 m 电缆模型200 m 处设置0.1 m 的缺陷，并分别对比了该方法在局部电容减小为电缆本体电容的0.9 倍时和局部电容增大为电缆本体电容的1.1倍时与传统FDR 和TDR 方法相比的故障定位准确率，其结果如表2所示。

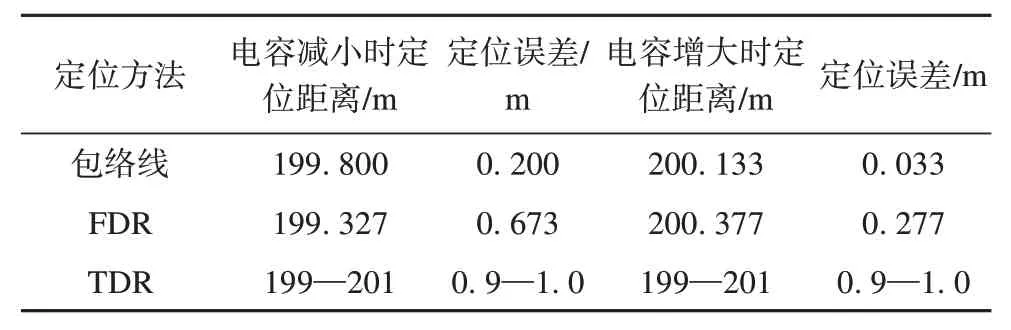
表2 不同方法关定位结果Tab. 2 Localization results of different methods

由表2的结果可得，与传统的FDR和TDR方法相比，包络线方法的定位精度更高，包络线方法由于对数据求对数及归一化后故障的峰值明显增大，包络线峰值最大点即与参考信号的时间中心相对应，且信号的时域包络线不会在传播过程中随着波形畸变发生变化，具有良好的传递性，而且其峰值点在求对数及归一化后其位置不会发生改变，由此其定位精度对比传统方法有了一定的提升。

2.2 信号的噪声抑制

在现场实际测试中往往会面临着现场各种复杂随机信号的干扰，并且由于硬件设备功率的限制以及信号在传输过程中的衰减，导致实际采集得到的反射信号幅值较为微弱，并且极易湮没在现场存在的白噪声［19］及其他噪声干扰中，导致定位效果不佳。为此本节针对参考信号所具有的特性展开讨论，并巧妙地利用时频域反射法参考信号的性质对其进行滤波处理。

白噪声的功率谱密度在整个频带范围内为常数，即信号在各频带范围内均存在一定的能量，是不能通过带通滤波对其进行消除的。为此针对现场可能存在的白噪声干扰，本文采用一种硬阈值法的自适应小波去噪算法［20］对信号进行初步的处理。白噪声的小波阈值为其中δ为信号首层小波分解系数均值除以0.647 5，N为信号的数据长度。首先利用示波器采集时域波形，然后进行小波基函数为db8 的5 层小波分解，通过消除噪声相关系数并保留与信号期望值密切相关的系数进行重构来实现对白噪声的滤除［21］，具体的去噪流程如图9所示。在此基础上对信号进行带通滤波处理。

图9 信号小波去噪流程图Fig. 9 Flow chart of signal wavelet denoising

由于本文所选用的参考信号为线性可调频信号，因此本文利用快速傅里叶变换（fast Fourier transform，FFT）对入射参考信号的频谱特性进行计算。通过对2.1 小节所述200 m 处局部电容减小的500 m 电缆模型进行分析，将入射信号和反射信号的频谱分别进行求取，得到的频谱特性曲线如图10所示。

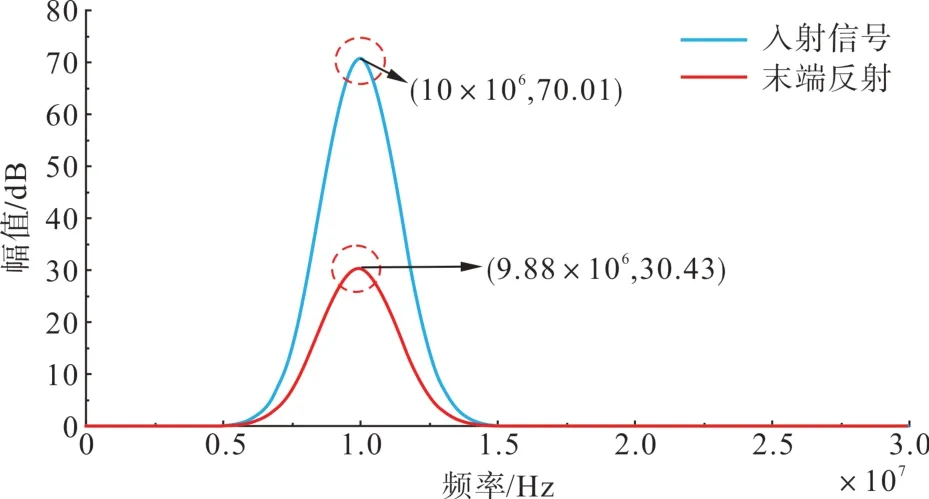
图10 入反射信号的频谱图Fig. 10 Spectrogram of incoming reflected signal

从图10 可知，该信号是具有固定频带宽度的窄带信号。为此，根据参考信号的这一性质可采用窄带滤波对数据加以处理以滤除实际测试时可能存在的干扰信号。求出信号的频谱后，本文通过八阶巴特沃斯带通滤波器进行带通滤波［22］，将滤波器的下限频率fn1和上限频率fn2分别设置为信号所在频带的最低和最大频率值，在得到滤波系数后，进行带通滤波，即可获得频带范围为fn1与fn2之间的期望波形Sfilter。

同时可以发现，信号在传输过程中反射信号的强度会因为衰减而大幅度削弱，但是信号的整体频带范围是不会发生改变的，同时末端反射的中心频率受到衰减和色散的影响，导致中心频率出现了降低。

3 包络线的定位实验

为验证所提包络线定位技术在实际电缆样本上的可行性，分别在50 m 长的10 kV XLPE 电力电缆和500 m 长的15 kV XLPE 电力电缆上进行测试。电缆的测试设备及测试示意图如图11所示。

图11 实际测试示意图Fig. 11 Schematic diagram of actual test

本文利用信号发生器产生相应的高斯包络可调频信号作为入射参考信号，信号发生器的信号为RIGOL DS5251，该设备性能优越，可产生最高50 MHz 的信号频率，最大输出电压幅值为20 V。信号数据采集设备选择示波器，其信号为RIGOL DS6104，最大采样率为5 GSa/s。为保证测试效果最佳，需要尽可能地满足测试线与被测电缆的缆芯与铜屏蔽层保持同轴结构，且保证测试线的分叉尽可能短，为此本文采用同轴信号测试线公头转双夹子线在测试时对电缆缆芯以及铜屏蔽层进行连接。

对于50 m 长的电缆，在距离测试端22.3 m 左右存在中间接头。由于电缆接头的电容小于电缆本体［23］，因此该段区域可视作局部电容减小的缺陷。实测信号选择中心频率f0=450 MHz，脉宽Ts=2×10-7s，频带宽度bs=300 MHz，示波器采集得到的实测信号如图12所示。

图12 50 m电缆示波器实测波形Fig. 12 Measured waveform of oscilloscope

对该信号进行去噪以及带通滤波处理后，利用希尔伯特变换求取实测信号的包络线，并通过2.1小节所述的定位技术进行处理，得到的去噪后时域波形以及包络线定位结果如图13所示。

对于500 m 长的电缆，在距离测试端180 m 左右存在中间接头。实测信号选择中心频率f0=50 kHz，脉宽Ts=2×10-7s，频带宽度bs=35 GHz。示波器采集得到的实测信号及去噪包络线定位结果如图14所示。

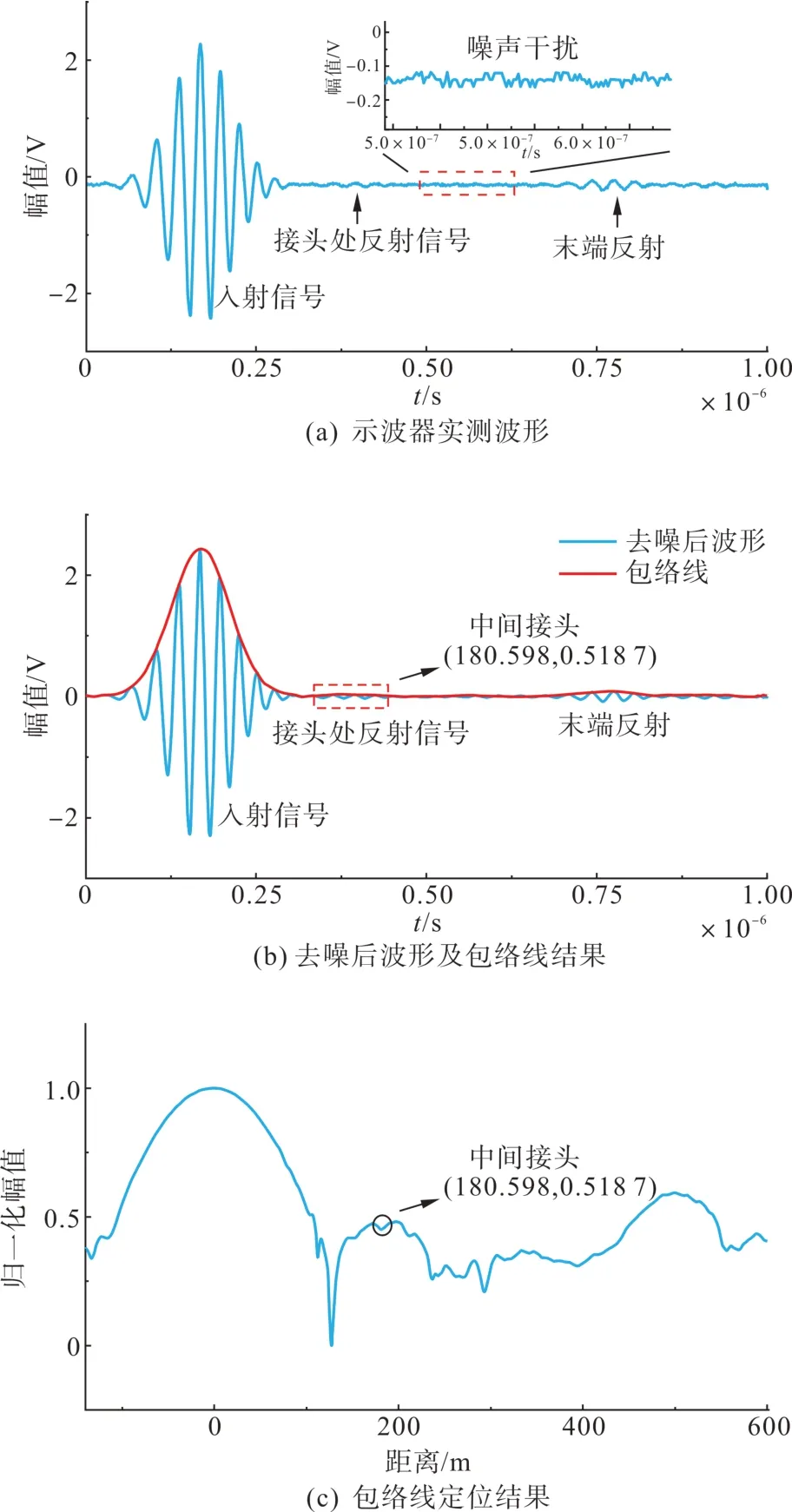
图14 实测500 m电缆实测波形及包络线定位结果Fig. 14 Time domain waveform and envelope positioning results after denoising of 500 m cable

同时利用单一高斯脉冲对50m 电缆进行TDR测试，以得到缺陷处的时域波形变化情况。得到去噪过后的TDR 测试波形如图15（a）所示，进而与TFDR 缺陷处的实测波形进行对比验证，得到的结果如图15所示。

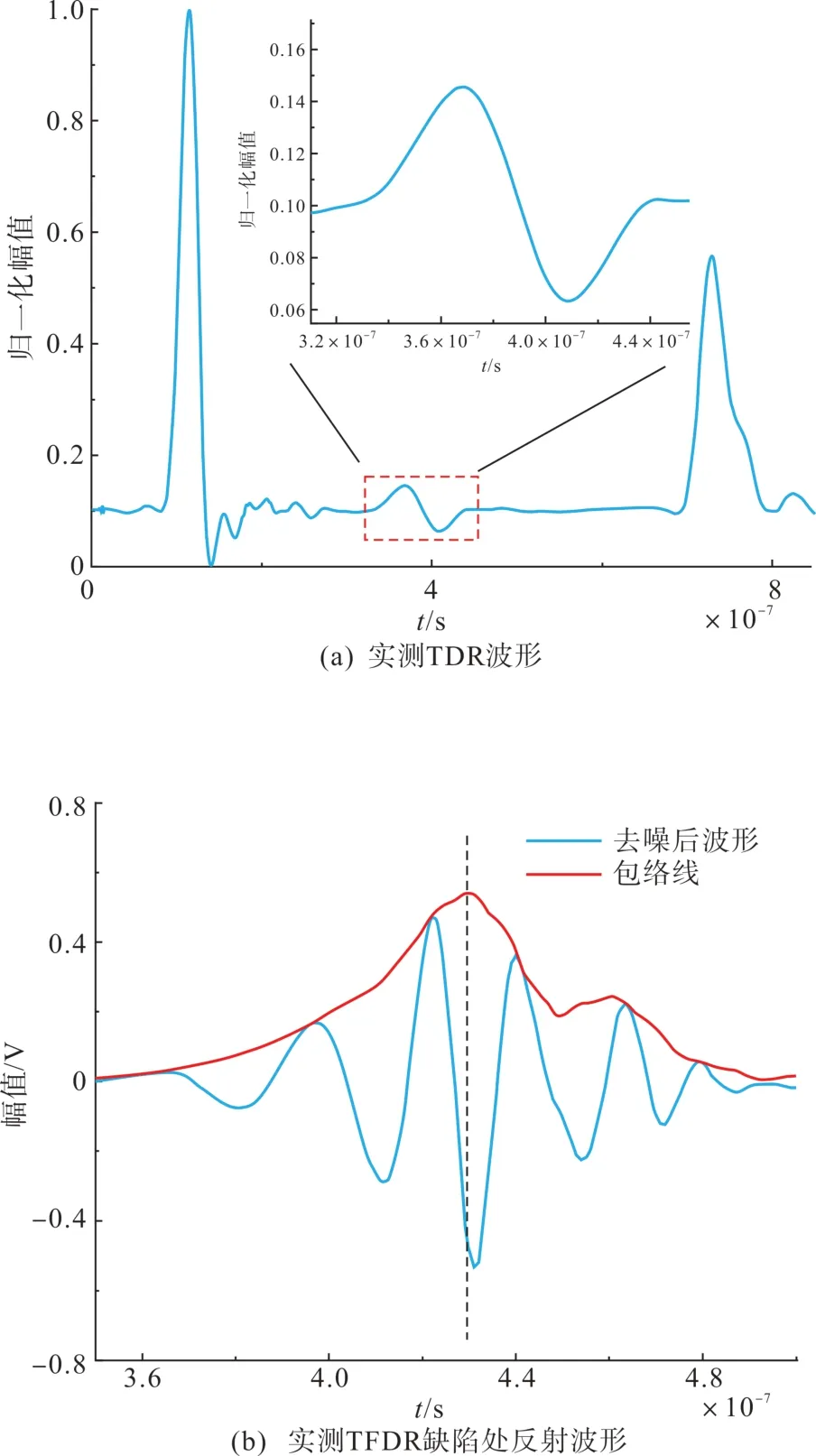
图15 缺陷处波形变化情况对比Fig. 15 Comparison of waveform changes at defects

由图15 可以看出，基于高斯包络的线性可调频脉冲可对电缆接头很好地进行定位识别，并且利用包络线对缺陷进行定位是可行的。由于中间接头可视为局部电容减小的区段［24］，该段位置对应的特性阻抗相较于电缆本体是增加的，因此从理论上分析单一高斯脉冲波形应呈现“先正后负”的波形，与图15（a）的实测波形相吻合。同时根据单一脉冲波形与TFDR 波形对比，可发现TFDR 的时域信号亦可对缺陷类型进行初步判断。因此说明本节所提包络线定位技术是可以针对电缆局部缺陷实现定位诊断的。

基于波形时域包络线的定位技术可以对电缆局部缺陷进行一定程度的定位诊断，且算法复杂度较小，运算速度快，使用便捷，可作为电缆缺陷诊断的初步探测手段以及局部缺陷定位的重要参考依据。

4 结论

本文首先对电缆传输线模型进行介绍，对电缆的分布参数等效电路进行了说明，并构建了电缆缺陷的仿真模型，推导了电缆的传递函数方便进一步分析电缆缺陷状态。对时频域定位方法进行了理论介绍，并对参考信号的特性进行了说明，探究了不同参数对参考信号波形的影响。在此基础上提出一种基于波形时域包络线的定位技术，其关键为时域噪声处理以及利用希尔伯特变换对时域包络线进行求取，并巧妙地利用对数坐标对定位结果进行显示，从而提高定位的分辨率。并且通过理论及仿真结果说明了局部电容增大或减小等不同缺陷类型对时域反射波形的影响。最后在电缆实际样本上进行试验，验证了本文所提方法对于电缆中间接头定位的有效性以及时域波形对缺陷类型判断的可行性。

在试验过程中也发现了很多问题，当测试的电缆比较长时，由于信号的衰减TFDR 对于故障的检测在噪声影响下比较微弱，去噪后虽然比去噪前有一定的效果，但是故障的检测对比短电缆也不够明显；对于现场实际在运电缆，其电缆长度将更长，缺陷状况也将更为复杂，且现场电缆的总长度信息可能是未知的，因此难以通过固定电缆的总长度来确定波速度，进而影响缺陷处的定位精度。因此后续可针对现场工程测试规范建立电缆初始数据库等展开研究，探究不同型号的电缆以及不同类型的缺陷段对电缆波速度的影响，以提高该方法的工程应用性。