计及热惯性的热电联产虚拟电厂韧性提升策略

于松源，张峻松，元志伟，房方*

（1.华北电力大学控制与计算机工程学院，北京市 昌平区 102206；2.西安热工研究院有限公司，陕西省 西安市 710061）

0 引言

为了应对极端天气对电力能源系统带来的不利影响，IEEE 电力和能源社会工作组针对电网、热网等关键能源基础设施提出了“韧性”的概念[1]。韧性表征系统抵御极端事件破坏，吸收、适应并于事后快速恢复的能力[2]。在建设新型电力系统的大背景下，电力系统和热力系统耦合程度不断加深[3-5]。热电联产虚拟电厂(combined heat and power-virtual power plant，CHP-VPP)[6]作为一种新兴的具有高度灵活性和适应性的电热耦合系统，机组布局分散、高度可控，在信息和通信技术支持下可实现电热能量的协同管理，为系统应对极端灾害提供了可能[7]。如何通过CHP-VPP 的热电特性协调能源的分配利用，从而提升系统韧性，是当前学术界关注的焦点。

韧性提升策略主要侧重于基础设施的投资和灵活性资源的整合[8-10]，然而，设备线路故障、可再生能源出力等诸多不确定性因素影响最优决策的制定。目前，大部分韧性提升策略研究采用随机规划[11-12]和鲁棒优化[13-15]。文献[16]考虑全时段不确定性影响，基于随机响应面法构建了混合整数二阶锥规划随机优化故障恢复模型，最大程度地减少了停电损失。文献[17]应用鲁棒优化的方法提出了综合能源系统在极端天气下的韧性提升模型，实现了系统韧性的提升。随机规划引入了不确定参数的概率密度函数，但其无法精确描述概率分布，且在进行大量的场景计算时会造成求解困难；鲁棒优化是在最恶劣情况下的最优出力计划，比随机优化求解效率更高，但不确定集的选择具有主观性，决策相对保守[18]。分布鲁棒优化[19]结合了随机规划和鲁棒优化的优点，既解决了概率分布无法精确描述的问题，同时又避免了最优解的过度保守。文献[20]提出了一种基于分布鲁棒优化的车-站-网能量管理与交易方法，构建了以多主体各自利益最大为目标的双层Wasserstein分布鲁棒互动博弈模型。文献[21]建立了基于典型场景的VPP-配电网分布鲁棒优化调度模型，解决了可再生能源出力及负荷不确定性的问题。然而，在当前研究中，分布鲁棒优化大多应用于优化调度方面，在提升系统韧性方面的研究还比较少。

由于CHP-VPP中供热管道、建筑物等热力元件中热能传输速度慢、惯性大，负荷侧温度变化相较于热能供给端具有一定的迟延，这种热能传输特性赋予了供热系统被动储热的能力，如果加以有效利用，将会降低系统的运行成本[22]。文献[23]建立了考虑热惯性的两阶段鲁棒优化调节模型，较好地兼顾了运行效率与稳定性。文献[24]构建了传输侧与负荷侧惯性影响下用户温度动态响应的多时间耦合特征双层模型，实现了可再生能源消纳并兼顾了用户用能体验。文献[25]提出一种考虑供热系统多重热惯性的电热联合协调优化策略，有效降低了电热耦合强度，提高了系统的灵活性和经济性。因此，当面临极端灾害时，可以利用热惯性特性提升电热协调互补能力[26]，促使系统快速恢复供能，减少切负荷，提高系统韧性。然而，现有关于热惯性的研究集中在系统建模、运行优化方面，未充分挖掘热惯性在系统韧性提升方面的作用。

综上所述，本文提出了考虑热惯性的CHPVPP 两阶段分布鲁棒韧性提升策略。第一阶段基于最小生成树理论对系统进行网络重构，制定联络开关通断计划，第二阶段是在最恶劣的故障场景下最小化系统成本。针对具有min-max-min 形式的非凸、非线性优化问题，采用列与约束生成(column-and-constraint generation，C&CG)算法进行迭代求解，并通过算例对比分析验证所提方法的优越性。

1 CHP-VPP两阶段韧性提升策略

传统单一能量系统的重构由于受到负荷分布及分布式电源出力的限制，系统供能恢复水平有限。CHP-VPP 由热电联产(combined heat and power，CHP)、光伏(photovoltaic，PV)、风机(wind turbine，WT)、热泵(heat pump，HP)等构成，不同于单一能量系统，CHP-VPP中电热负荷可由异质子系统供给，实现能量转供，且CHP机组等耦合元件可调整电热出力，为CHP-VPP提供电源支撑，优化系统运行状态，进而提升CHPVPP负荷恢复水平。

为了提升CHP-VPP 在应对极端天气时的容灾能力，本文将CHP-VPP 韧性提升策略按时序划分为抵御-响应-恢复3 层，如图1 所示。在抵御层，CHP-VPP 制定联络开关通断计划，当极端天气使传输线路中断时，作为中断线路的冗余线路，在符合配电网“闭环设计，开环运行”的原则下，提供整个系统能量可冗余流通路径。在响应层，最大化考虑极端天气对CHP-VPP 的预期破坏，即选择最严重的故障概率分布情景，进而使最终的调度决策适应于所有故障情况。在恢复层，以开关通断成本、切负荷成本和机组运行成本最小为目标函数，对各机组出力值、消纳风光发电量以及切电负荷、热负荷等情况做出决策。

图1 CHP-VPP韧性提升策略Fig.1 Resilience enhancement strategy of CHP-VPP

2 CHP-VPP分布鲁棒韧性提升模型

2.1 CHP-VPP韧性提升目标函数

本文定义CHP-VPP的韧性指标为系统应对极端天气过程所产生的总成本。CHP-VPP韧性提升策略旨在最大限度地保障最恶劣天气下系统负荷的持续供应。CHP-VPP两阶段三层韧性提升模型的目标函数表示如下：

2.2 抵御层约束条件

为保证供电可靠性，对模型进行网络重构时运行方式必须满足辐射状运行的条件。采用Prim算法[27]搜索最小生成树，其数学公式表示如下：

式中：xij表示节点i到j的线路连接状态，当xij=1时，节点i、j之间的线路为连接状态；nTotal、nTree分别为节点总数和根节点数；Φe表示电网线路集合。

2.3 恢复层约束条件

2.3.1 电网约束

1）电功率平衡约束如下：

2）传输功率与相角约束如下：

3）与上层电网交易约束为

4）节点电压与线路电流约束如下：

式中：Ui表示节点i的电压；Ui，max和Ui，min分别为Ui的上、下限；Iij，t表示t时刻线路ij的电流；Iij，max为t时刻线路ij电流的上限。

2.3.2 机组运行约束

1）CHP机组运行区间约束为

式中：Hmax表示CHP热出力最大值；Pmin、Pmax分别表示CHP 电出力最小值和最大值；Hmed、cm、cn和cv均为CHP机组运行区间常数。

2）CHP机组爬坡率约束为

3）HP出力约束为

4）蓄电池约束如下：

2.3.3 热网约束

1）热功率平衡约束

为了保证供热侧热功率的供需平衡，其约束为

2）供热管网热传输迟延

基于改进的节点法对一次热网热水传输迟延进行建模，热传输迟延tdelay相当于热水从管道入口到管道出口流过的时间，用积分表示为

式中：Dg、Lg分别为管道g的直径和长度；mg为管道g中水的质量流量；ρw为热水的密度。本文热水调节方式采用质调节，求解式(22)得到传输迟延时间为

为使模型简化，将迟延时间与调度时间的整数倍相匹配，将管道出口温度分成两部分[30]，并计算这两部分之和，如式(24)所示。同时，对(tdelay/Δt)进行取整，将迟延时间分成(tdelay/Δt)-[tdelay/Δt]和[tdelay/Δt]两部分。管道g的出口温度表示如下：

式中：λ1、λ2为权重系数；[·]为取整函数；Δt为一个调度周期。

3）供热管网热传输损耗

供热管网埋在土壤之中，与周围环境存在温度差，因此在能量传输过程中会与周围环境发生热交换，从而损失一部分热能[31]。本文忽略管内热水沿着管道纵向方向的温度变化，建立横向方向温度变化的模型[32]，该模型的偏微分方程可表示为

求解式(27)，得到管道出口温度与入口温度关系表达式为

4）建筑物惯性建模

本文考虑的建筑物热惯性主要为建筑物围护结构热损失和冷风渗透热损失：建筑物围护结构热损失是指围护结构通过热辐射、热对流等与外界低温环境进行热交换造成的损失；冷风渗透热损失是指外界冷风通过门缝、窗户等进入室内，导致室内温度降低从而造成的热损失。

建筑物热动态特性[33]可表示如下：

围护结构热损失包含与外界进行热交换的热损失及修正热损失，其中修正热损失包括高度附加修正、风力附加修正和朝向修正热损失，围护结构热损失可表示为

式中：ℓb、μb、Sb分别表示围护结构的温差修正系数、热传导系数、面积；xhei、xori、xwd分别表示建筑高度附加修正率、朝向修正率、风力附加修正率；表示建筑物室外温度。

冷风渗透热损失使用缝隙法计算，其原理为根据进入室内的冷空气的风压和热压来计算热损失。缝隙法计算热损失表示为

式中：ρair、cair分别表示空气的密度和比热容；Vb表示建筑物室内面积。

综合式(30)—(34)，通过向后差分法，可得到如下关系表达式：

式中a1、a2、a3、a4分别为室内温度、供水温度、回水温度、室外温度对当前室温的影响因子。

为保证室内用户舒适度，室内温度应该保持在如下范围内：

2.4 两阶段韧性提升模型求解

2.4.1 两阶段韧性提升模型

为方便表达，将所提出的两阶段韧性提升模型以矩阵形式描述如下：

式中：x为第一阶段决策变量向量；U为描述线路故障的分布鲁棒模糊集；u为不确定性参数向量；b、c均为系数向量；yr为线路故障场景为r时的第二阶段决策变量向量，如式(4)所示；R为场景总数，即目标函数式(1)中的max项。

1）模型抵御层约束为

式中：A、d分别为系数向量、系数矩阵；Sx为决策变量向量x的集合。该式包括式(5)和(6)。

2）模型响应层约束为

3）模型恢复层约束为

式中：Sy为决策变量向量yr的集合；D、H、E、M均为系数矩阵。该式包括式(7)—(21)、(24)—(26)、(28)、(29)、(35)、(36)。

2.4.2 模糊集线性化

由于模糊集范数约束中含有绝对值，为方便求解，将其转化为线性约束。引入来分别表示pr相对于的正偏移量和负偏移量；引入l+和l-来分别表示L1范数的正偏移和负偏移标志；引入s+和s-来分别表示L∞范数的正偏移和负偏移标志。此时式(39)中L1范数和L∞范数约束可重新表示为

2.4.3 基于C&CG算法的求解策略

所构建的CHP-VPP两阶段分布鲁棒韧性提升模型具有3 层结构，本文将整个模型划分为主问题和子问题。主问题描述如下：

式中：ς为辅助变量；yr，l为第r个场景第l次迭代新添加的决策变量，l=1，2，...，v，其中v为最大迭代次数；Ο为解空间，初始值为空集，下一次迭代后Ο=Ο∪{v+1}；u*为最恶劣场景。

由于子问题各场景之间相互独立，子问题描述如下：

求解式(46)和式(47)后，可得最恶劣故障概率分布，结合主问题，采用C&CG 算法[26]可直接进行迭代求解。

3 算例分析

3.1 系统参数

为验证所提出方法的有效性，将两阶段分布鲁棒韧性提升策略应用在IEEE-33 节点电力系统+6 节点供热系统中，如图2 所示。按照《供配电系统设计规范》[34]划分电、热负荷等级，其中E2、E3、E5、E6、E9、E15、E18、E25、E33、H1、H2 为一级负荷；E8、E10、E13、E14、E16、E19、E23、E26、E28、E31、E32、H3 为二级负荷；其余为三级负荷。选择典型日的电热负荷、风光出力及室外温度数据进行模拟，如图3所示。建筑物室温允许波动范围为18～22 ℃，各机组参数详见文献[35]。

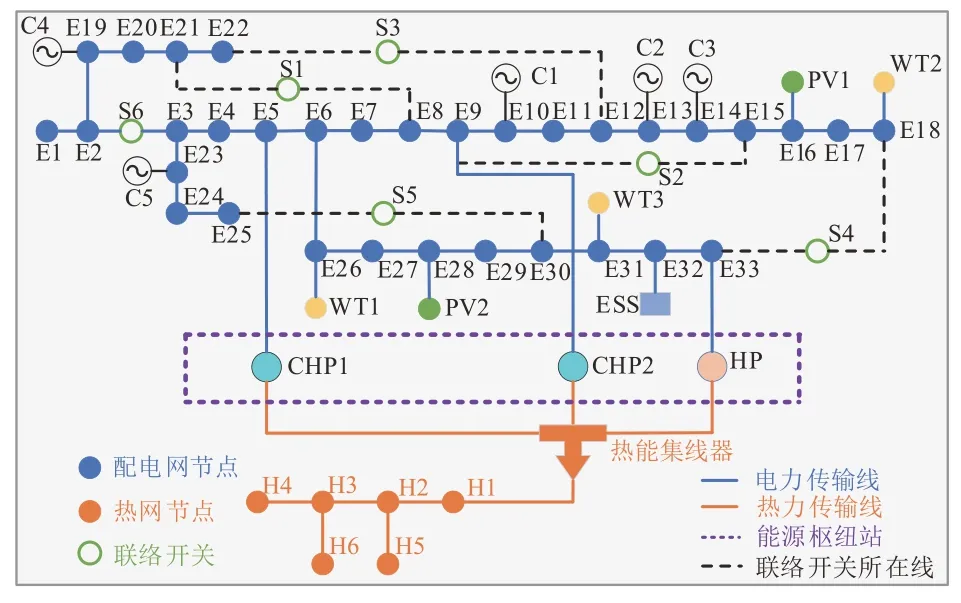
图2 CHP-VPP测试系统框架Fig.2 CHP-VPP test system framework

图3 电热负荷、风光出力及室外温度情况Fig.3 Electric load,heat load,wind output,solar output and outdoor temperature

3.2 仿真结果

3.2.1 决策结果

假设CHP-VPP 在06:00 发生故障，故障持续4 h，θ1=0.5，θ∞=0.99，此时主问题和子问题均为线性模型，使用Yalmip 工具箱调用Cplex 求解器进行求解即可。

在故障发生前，CHP-VPP充分利用联络开关进行网络重构，增加联络开关操作，不断拓展电力传输线路的传输路径，联络开关状态如图4所示。

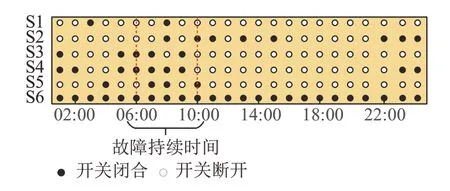
图4 基于分布鲁棒优化的联络开关状态Fig.4 State of interconnection switch based on the distributionally robust optimization

基于分布鲁棒优化的CHP、HP、电池的出力情况如图5所示，常规机组出力如图6所示。在故障发生的06:00—10:00，CHP 机组电出力和热出力增加，HP出力减少，以提高系统供电能力，保证切负荷损失达到最小。

图5 基于分布鲁棒优化的CHP、HP和电池出力情况Fig.5 CHP,HP and battery output based on distributionally robust optimization

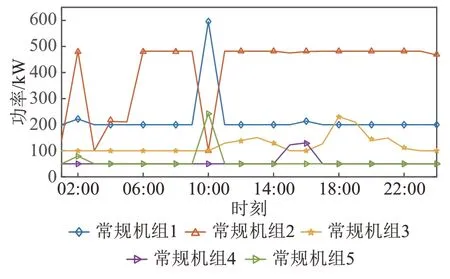
图6 基于分布鲁棒优化的常规机组出力情况Fig.6 Conventional units output based on the distributionally robust optimization

需要说明的是，调度时间为10:00时，连接在节点19 处的常规发电机组1 出力上升，连接在节点23处的常规发电机组2出力下降，如图7所示。这是因为此时连接在31节点处的可利用的风电场功率上升，为促进风资源消纳，风电场增加出力，通过节点31→30→25→24→23的传输线路传递至23 节点，从而导致常规发电机组2 出力下降，进而导致线路23→3→2→19传输到节点19的电功率下降，因此，常规发电机组1 需要增加出力以使节点19能量平衡。

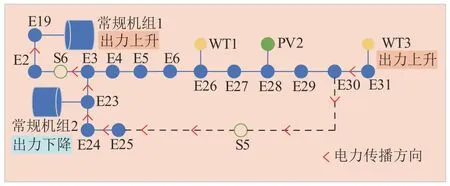
图7 电力节点局部放大图Fig.7 Partial enlarged view of power nodes

为了分析热惯性对CHP-VPP 决策结果的影响，设置了不考虑热惯性的对比实验，实验的室内温度限制在20 ℃。热惯性对CHP-VPP 各项成本的影响如表1所示。

表1 热惯性对CHP-VPP各项成本的影响情况Tab.1 Impact of thermal inertia on the cost of CHP-VPP

由表1 可以看出，当考虑建筑物热惯性时，CHP运行成本、HP运行成本、切负荷成本、总成本均大大减小，弃风光率下降到5.02%。这是因为热惯性具有延迟特性，且人体舒适度可以在一定范围内波动，因此不要求热负荷保持实时平衡，而是维持在动态范围内即可，由此增加了系统的调度灵活性，使得在风光出力峰值时减少机组的运行功率，提高风光的消纳水平，降低在故障期间的切负荷成本。

3.2.2 不同置信水平对比分析

当置信水平不同时，模型的概率允许偏差值θ1、θ∞也不同。计算θ1在[0.2,0.8]波动，θ∞在[0.5,0.99]波动时的分布鲁棒优化总成本，结果如表2所示。

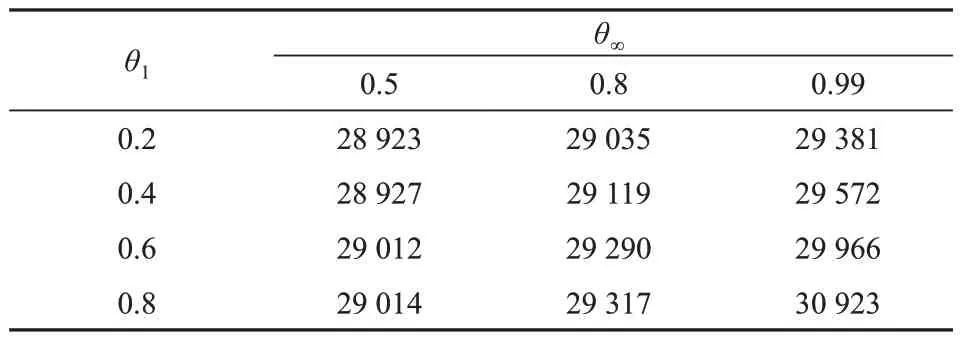
表2 不同置信水平下系统总成本Tab.2 Total cost of the system at different confidence levels 元

从表2可以看出，随着置信度θ1和θ∞的增大，系统的总成本增加。这是因为置信度的增大导致概率允许偏差值增大，使不确定范围增大，系统为满足最恶劣情况下的安全稳定运行，增加了机组出力，减少了可再生能源的消纳，因此各项成本增加，造成总成本增加。

3.2.3 不同优化方法对比分析

为了比较不同优化方法的影响，选取了确定性优化方法作为对比。以分布鲁棒优化和确定性优化2种方法各自所获得的联络开关状态为基础，选取导致线路7—8、线路3—4、线路16—17故障的3 个极端天气场景，计算失负荷量及机组运行成本。2 种优化方法得到的联络开关状态分别如图4和图8所示。对比可知，确定性优化方法由于未考虑极端天气来临时的线路故障状态，联络开关在故障持续时间内不会提前动作，开关状态主要受到可再生能源出力及负荷需求影响。

图8 基于确定性优化方法的联络开关状态Fig.8 State of interconnection switch based on deterministic optimization method

进一步，本文选用切负荷成本来表征系统韧性。表3对比了分布鲁棒优化和确定性优化2种方法在3 个场景下的切负荷成本及机组运行成本情况。可知，确定性优化方法忽略了线路故障的影响，任意一条线路的断开都导致了大量切负荷情况发生，使切负荷成本大大提高，严重影响了CHP-VPP的安全稳定运行。相比之下，分布鲁棒优化方法考虑到线路故障，提前制定了联络开关通断策略，增大了机组出力，使得系统在线路7—8及线路3—4断开的情况下，切负荷成本为0，在线路16—17 断开时减少了切负荷成本，3 种情况下系统总成本均较低，由此证明了所提出的基于分布鲁棒优化的韧性提升策略的有效性。

表3 3种极端情况下机组运行成本及切负荷成本情况Tab.3 Unit operating costs and load shedding costs under three extreme scenarios

4 结论

提出了CHP-VPP两阶段分布鲁棒韧性提升策略，第一阶段以联络开关通断为决策变量，在极端天气来临前进行网络重构，第二阶段在最恶劣场景下制定出力计划，充分利用各种灵活性资源，制定最优出力计划，并采用C&CG 算法进行迭代求解。通过在IEEE-33 节点电力系统+6 节点供热系统上进行算例分析，得到如下结论：

1）CHP-VPP 韧性提升策略加入对热惯性的考虑，不仅减少了极端天气下系统切负荷损失，降低了系统运行成本，还提高了风光消纳水平，增加了系统的调度灵活性。

2）置信度影响分布鲁棒模糊集的置信区间，置信度越高，场景的概率允许偏差值越大。CHPVPP 系统为满足最恶劣情况下的安全稳定运行，增加了机组出力，减少了可再生能源的消纳，从而使总成本增加。

3）基于分布鲁棒优化的韧性提升方法提前制定了联络开关通断策略，降低了CHP、HP等机组的运行成本，减少了系统的切负荷量，提升了系统极端天气下的韧性。