基于交替方向隐式平衡截断法的直驱风电场次同步振荡分析的模型降阶研究

王进钊，严干贵，刘侃

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学），吉林省 吉林市 132000）

0 引言

近年来，构建以新能源为主体的新型电力系统被作为能源电力行业实现碳达峰、碳中和的主要措施[1-4]。我国风电发展迅猛，截至2021年11月14日，我国风电并网装机容量达到30 015万kW，突破3 亿kW 大关，15 年间装机容量增加了近百倍，年均增速30%左右。据行业权威机构预测：风电并网装机容量到2030 年将达8 亿kW，到2060 年将达30 亿kW。2013 年以来，我国河北沽源风电系统屡次发生3～10 Hz 的次同步振荡(subsynchronous oscillation，SSO)，曾造成上千台风电机组异常脱网。2015 年7 月1 日，我国新疆哈密地区风电集群发生跨越5 个电压等级的次/超同步振荡事故，造成花园电厂3台660 MW机组全切的严重后果。近年来，风力发电的渗透率占比持续攀升，使得风电并网引发的新型次同步现象不断危害电网的安全稳定运行[5-10]。

在一个由直驱风机构成的风电场中，若对风电机组构建详细的数学模型需要上千个微分方程，“自下而上”堆积木式的建模方法面临“维数灾”问题，仿真计算代价大，并且海量仿真结果难以分析，尤其是机群在功率振荡中的作用难以估量，使得搭建模型的有效性难以检验。因此，建立一个能够捕获高阶系统重要动态的风电场降阶模型对系统研究具有重要意义。模型降阶方法在满足问题分析需要的同时，将一个较大系统转化为一个近似的较小系统，使得降阶后的系统仿真时长和方程维数大大降低[11]。常见的模型降阶方法有如下3种[12]：

1）基于奇异值分解(singular value decomposition，SVD)的方法。该方法主要包括平衡截断(balanced truncation，BT)法和基于交替方向隐式(alternating direction implicit，ADI)的平衡截断法。

2）Krylov子空间类方法。该方法主要包括有理克雷洛夫(rational Krylov，RK)算法和迭代有理克雷洛夫算法(iterative RK algorithm，IRKA)。

3）模态截断方法。该方法识别系统特定的模式，并且将模式保留下来。

针对实际出现的振荡问题，国内外开展了广泛研究。在风电场建模方面，主要有聚合建模和降阶2 种。聚合建模又分为单机等值模型和多机等值模型，多用于稳态潮流计算和暂态计算，较早一些用于振荡分析的等值模型采用的是单机等值模型。由于次同步振荡现象是“场-网”作用结果，采用单机等值模型后，对于源网耦合作用考虑不足，尤其当电网强度较弱时，等值模型有效性值得商榷；另外，等值理论依据不足，如何证明风电场等值前后主导振荡特性一致也有待分析。在风电场的降阶模型中，最初采用基于聚合的方法，该方法可进一步分为单机聚合和多机聚合[13-15]。此外，文献[16]应用模态分析法，通过分析并保留特定需要的模式，模拟风电机组输出功率的降阶。文献[17]应用奇异值摄动的方法对复杂电力系统进行模型降阶研究。文献[18]应用Krylov 子空间类方法对系统进行模型降阶研究。但是目前对于面向直驱风电场次同步振荡分析的模型降阶研究鲜见报道，值得更加深入的研究。

本文建立一种面向直驱风电场次同步振荡分析的降阶等值模型，采用基于ADI 的平衡截断方法对风电场模型进行降阶分析，在直驱风电场次同步振荡稳定场景下验证该降阶方法的有效性，从降阶模型阶数、计算耗时等方面对比该降阶方法的应用效果。

1 直驱永磁同步风电场模型的建立

1.1 直驱式永磁同步风电机组结构

直驱式永磁同步风电机组结构如图1 所示，包括风轮机、永磁同步发电机(permanent magnet synchronous generator，PMSG)、四象限型变流器等[14]。其中：AC 表示交流电(alternating current)；DC 表示直流电(direct current)；PWM 表示脉冲宽度调制(pulse width modulation)；u1和i1分别为发电机侧的电压和电流；u2和i2分别为电网侧的电压和电流；Udc和Udcref分别为直流侧两端的电压及其参考值；P1，ref和Q1，ref分别为发电机侧输出的有功功率、无功功率参考值；Q2，ref为电网侧输出的无功功率参考值；ωr为发电机转子转速。

图1 直驱永磁同步风电系统示意图Fig.1 Diagram of direct drive permanent magnet synchronous wind power system

1.2 风力机的风能捕获模型

风力机通过叶片捕获风能，叶片固定在风力机轮毂处，假设轮毂处风速为v0，则风力机所捕获的风功率为

式中：Cp为风能利用系数，是风力机叶片从自然风能中所吸收能量与叶片扫过面积内未扰动气流所具有动能之比，是表征风力机捕获风能大小的一个量；Pw=，为风功率，其中m为风质量；ρ为空气密度；A1=πR2，为风力机叶片扫掠面积，其中R为风力机叶片半径。

在风速恒定的情况下，风机捕获的机械功率取决于Cp的大小。对于变速风力发电机组，Cp直接与叶尖速比λ、桨距角β有关，表达式如下：

桨距角控制系统数学模型可用以下方程表示：

式中：β0为初始桨距角；Tsq为惯性时间常数。

1.3 直驱式永磁同步风电机组模型

为建立永磁同步发电机数学模型，对定子绕组回路电压电流、磁链正方向进行以下规定：定子绕组电压、电流正方向为非关联参考方向；定子负值电流产生正值磁链。

两相旋转坐标系下电压方程为：

式中：U1d、U1q分别为d、q轴定子绕组电压；Rs为定子绕组电阻；i1d、i1q分别为d、q轴定子绕组电流；ψsd、ψsq分别为d、q轴定子绕组磁链。

将旋转坐标系d轴定在转子磁链方向上，定子磁链可表示为：

式中：Lsd、Lsq分别为d、q轴定子绕组电感；φ为转子磁链。

将式(6)代入式(5)可得：

根据牛顿运动定律，转子运动方程为

式中：Tm为原动机加于电机轴的机械力矩；Te为发电机电磁力矩；Ωm为转子机械角速度；J为转子的转动惯量。

在直驱式永磁同步风电机组拓扑结构中，发电机侧变流器控制结构如图2 所示，一般采用基于转子磁链定控制策略实现d、q轴解耦控制，由发电机侧输出的有功功率、无功功率参考值经过PI控制器之后，形成d、q轴电流分量参考值i1dref、i1qref，d、q轴电流分量及其参考值经过PI 控制器之后，得到d、q轴机端电压分量。

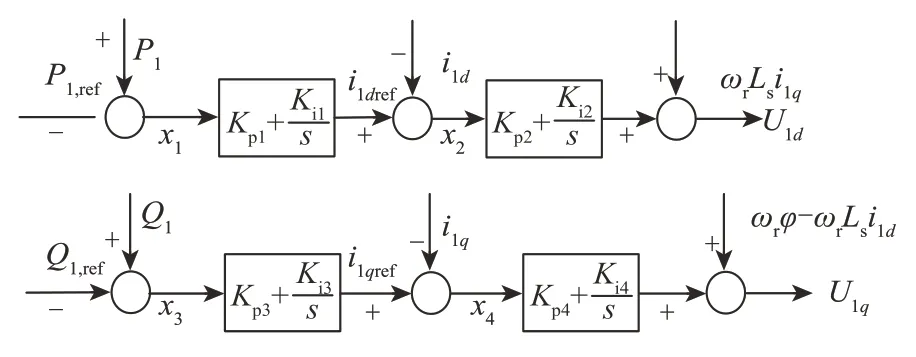
图2 发电机侧变流器控制框图Fig.2 Control block diagram of generator side converter

发电机侧变流器的数学模型表示如下：

式中：x1、x2、x3和x4为发电机侧变流器的控制参数；P1和Q1分别为发电机侧变流器输出的有功功率和无功功率；ΔPe和ΔQe分别为发电机侧变流器输出的有功功率增量和无功功率增量；Kp1,Ki1,Kp2,Ki2,Kp3,Ki3,Kp4,Ki4为PI控制器的控制参数；Ls为发电机定子电感。

在直驱式永磁同步风电机组拓扑结构中，电网侧变流器控制结构如图3 所示，采用并网点电压矢量控制，直流电压及其参考值经过PI控制器后，形成d轴电流分量参考值i2dref，d轴电流分量及其参考值经过PI 控制器后，得到d轴网侧电压分量；网侧无功功率及其参考值经过PI控制器后，形成q轴电流分量参考值i2qref，q轴电流分量及其参考值经过PI控制器后，得到q轴网侧电压分量。

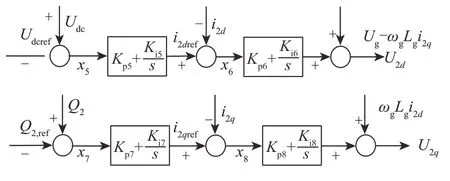
图3 电网侧变流器控制框图Fig.3 Control block diagram of grid side converter

电网侧变流器的数学模型表示如下：

式中：U2d和U2q分别为电网侧变流器的d、q轴电压；i2d和i2q分别为电网侧变流器的d、q轴电流；x5、x6、x7和x8为电网侧变流器的控制参数；P2和Q2分别为电网侧变流器输出的有功功率和无功功率；ΔQg为电网侧变流器输出的无功功率增量；ΔUdc为直流侧两端的电压增量；Ug为电网电压；Kp5,Ki5,Kp6,Ki6,Kp7,Ki7,Kp8,Ki8为PI控制器的控制参数；Lg为电网侧变流器进线电抗器的电感；ωg为电网同步角转速。

在直驱式永磁同步风电机组拓扑结构中，直流侧电容C的数学模型表示如下：

1.4 并网风电场线性化状态空间模型

i台直驱风电机组的线性化状态空间可表示为：

式中xi、ui、yi分别为第i台直驱风电机组的状态变量、并网点电压和输出电流。状态向量x=(β，ωr，x1，x2，x3，x4，Udc，x5，x6，x7，x8)T；输入向量u=(U1d，U1q，U2d，U2q)T；输出向量y=(i1d，i1q，i2d，i2q)T。

忽略集电线路的电阻，风电场网络方程可表示为

式中：uw为所有直驱风电机组的并网点电压构成的列向量；yw输出电流构成的列向量；Zk为集电线路的阻抗。

2 基于ADI的平衡截断方法

线性化后的状态空间表示如下：

式中：A∈Rn×n为状态矩阵；b∈Rn×t为输入矩阵；cT∈Rm×n为输出矩阵；x(t)∈Rn为系统的状态向量；u(t)∈Rt为系统的输入向量；y(t)∈Rm为系统的输出向量。

原始系统(22)根据变换矩阵V和W可以得到其降阶系统，一般表示为：

式(24)的传递函数可表示为

得到其降阶系统后，式(25)的传递函数可表示为

一般情况下，传递函数Hk(s)是传递函数H(s)的近似，降阶系统与原系统在次同步频段内保持相同的性质，并且降阶系统的阶数k要远远小于原系统阶数n，降阶算法过程耗时较短，计算速度较快。

平衡截断方法[19-22]最早由Moore提出，该方法首先通过计算系统的可控性和可观性Gramian 矩阵，得到系统的Hankel 奇异值(Hankel single values，HSV)，并以此为标准找到对系统输入、输出影响较小的状态；然后构造平衡变换矩阵，对系统进行平衡变换；最后将对系统输入、输出影响较小的状态从平衡变换后的系统中截断，从而达到模型降阶的效果。平衡截断方法实现降阶过程的步骤如下：

1）通过解李亚普诺夫方程(28)得到可控的格莱姆矩阵P与可观的格莱姆矩阵Q。

2）根据P、Q以及式(29)，计算全部的奇异值σi(i=1，2，…，n)。

当存在一个正整数q，使得σq远大于σq+1时，q就是理想降阶阶数。

3）应用式(30)进行Cholesky 分解，根据得到的Lc、Lo以及式(31)，进行SVD分解。

4）计算平衡矩阵T，并对状态矩阵A、输入矩阵b和输出矩阵cT进行平衡变换，得到。对平衡变换后的系统状态矩阵进行截断，得到降阶系统状态空间。

平衡截断方法的优点在于有明确的指标确定阶数，同时降阶系统可以保持原系统的可控性、可观性以及稳定性。但是其缺点是求解李亚普诺夫方程过程非常缓慢，这在处理大型风电场系统时不可行，利用低阶矩阵近似求解P与Q，可以解决这个问题，这种方法称为ADI。

ADI 迭代最初用于求解一个线性方程组，为了符合ADI迭代规律，这里将式(28)改为

因此，这个迭代方程表示如下：

式中αi为移位参数，将方程(33)合并成一个方程：

此外，在平衡截断方法中，目标是计算P的低秩因子分解，假定Lc，0=0且Lc，iLc，iT=Pi，式(34)可以直接写成：

同理，按照以上步骤也可计算Q的低秩因子分解。

3 仿真算例分析

为了验证基于ADI的平衡截断方法的实用性，本次仿真选取并联式集电线路的100 台金风1.5 MW 直驱风电机组来组成算例风电场，其中100 台直驱风电机组参数及控制策略完全相同。风速在4～8 m/s，以0.01 m/s 为步长随机分布；集电线路长度在400～800 m，以1 m 为步长随机分布。在式(22)的基础上，以场内第1台直驱风机的直流电压扰动Δudcref1作为输入，将风电场总输出功率增量ΔPΣ作为输出，可得如下状态空间：

式中：ΔX为全系统状态变量增量；Ar为状态矩阵；Br为输入矩阵；Cr为输出矩阵。

构建面向直驱风电场次同步振荡分析的降阶模型并应用在仿真分析中，通过对比系统降阶前后次同步振荡模式、Bode图及时域仿真波形的吻合情况，验证该降阶方法的有效性，从降阶模型阶数、计算耗时等方面分析该降阶方法的实用性。

3.1 直驱风电场次同步振荡分析的模型降阶

本文采用ADI 迭代的方法，以克服平衡截断法求解李亚普诺夫方程过程缓慢的缺点，在进行降阶之前，需要寻找恰当的移位参数αi以保证在ADI 迭代中精度最高且速度最小。计算环境采用DESKTOP-232GOKN，Windows 10 系统，4 GB内存，Intel(R) Core(TM) i5-6300HQ的CPU。通过大量算法演示，最终确定移位参数αi为39 时，ADI迭代效果最佳。100台风机系统庞大，利用传统方法求解李亚普诺夫方程一般需要37.83 s，本次仿真利用ADI 迭代方法求解李亚普诺夫方程则需要12.11 s，计算速度大大提高。

在Simulink 上搭建风电场模型，仿真实现100 台直驱风电机组联网仿真，利用Matlab 计算平台自带算法对风电场系统系数矩阵AW的Hankel奇异值进行求解，如图4(a)所示。同时，利用ADI迭代方法对AW的Hankel奇异值进行求解，如图4(b)所示。图4(c)为图4(b)的局部放大图。由图4(a)、(b)可见，2 幅图的数据分布情况大致相同，这说明用ADI 迭代方法求解李亚普诺夫方程与传统求解方法所得到的结果基本一致。同时，通过观察图4 可知，Hankel 奇异值在第3、6、11 阶时有了显著的下降，因此可将3、6、11阶作为降阶的目标阶数。

图4 风电场Hankel奇异值Fig.4 Hankel singular value of wind farm

通过Hankel 奇异值得到目标阶数之后，分别将降阶得到的3、6、11阶风电场等值降阶系统与升压变压器相连并接入电网中，图5 为风电场仿真接线图，表1为直驱风电机组参数，表2为风电场模型参数。

表1 直驱风电机组参数Tab.1 Direct drive wind turbine parameters

表2 风电场模型参数Tab.2 Wind farm model parameters

图5 风电场仿真接线图Fig.5 Wind farm simulation wiring diagram

3.2 仿真结果及分析

6阶降阶系统的状态空间表示如下：

图6 为全阶系统与风电场降阶系统Bode 图对比曲线。其中，6 阶与11 阶风电场降阶系统在次同步频段内与全阶系统基本吻合，而3 阶降阶系统与原系统相差较多，3、6、11 阶风电场降阶系统都能够捕获频率的峰值40.445 1 Hz，因此降阶目标阶数选择6阶。

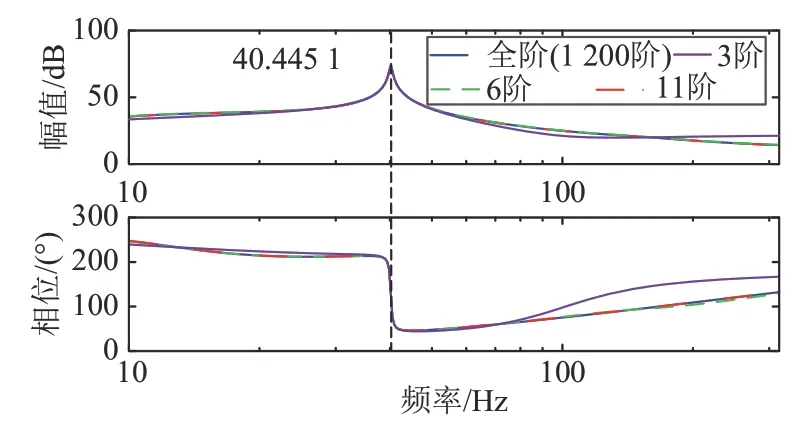
图6 全阶系统与降阶系统Bode图Fig.6 Bode diagram of full order system and reducedorder system

为了更好地验证降阶模型保持系统的主导振荡特性，本文以全阶模型和降阶模型对应特征根的平均欧氏距离作为衡量降阶模型准确度的指标。降阶模型的主导特征根应当与全阶模型的主导特征根尽可能地接近，即平均欧氏距离越小，降阶模型的降阶效果越好，降阶的准确度越高。平均欧氏距离的表达式为

式中：λm，e和λm，i分别为降阶模型和全阶模型的主导特征根；n为振荡特征根的数量。

特征值分布中次同步振荡模式对应的几何距离小于10-7，次同步振荡模式得到了保持。图7为6阶与全阶系统的特征值对比。图8为6阶与全阶系统的时域波形对比。

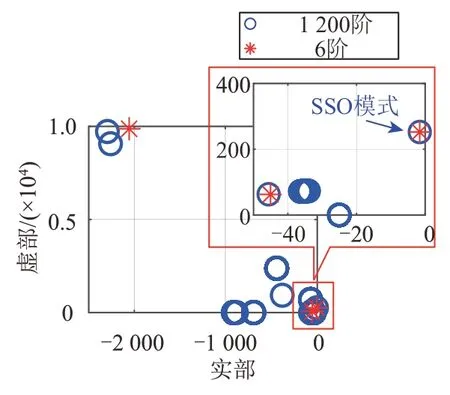
图7 6阶与全阶系统的特征值对比Fig.7 Comparison of eigenvalues of 6th order and full order systems

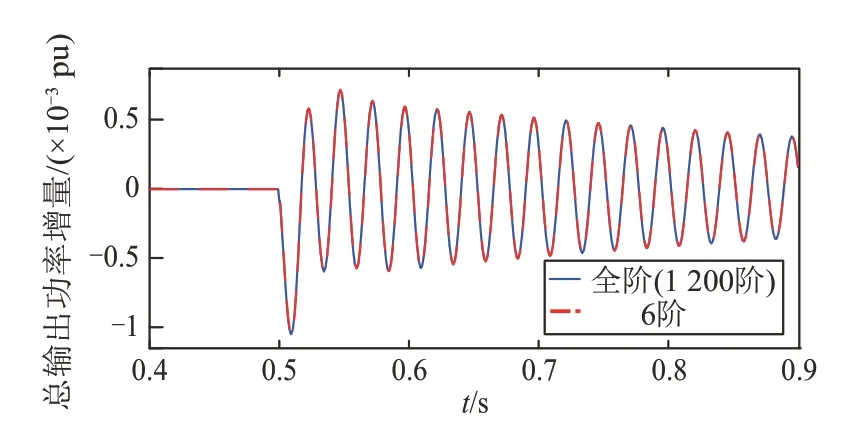
图8 6阶与全阶系统时域波形对比Fig.8 Comparison of time-domain waveforms of 6th order and full order systems

从图7可以看出，在特征值分布中，全阶模型的次同步振荡模式为-1.932 4+239.287j，降阶模型的次同步振荡模式为-1.935 6+239.287j，说明次同步频段内的特征根在降阶系统中得到了保留，筛选出了对系统次同步特性影响较大的特征根。从图8可以看出，t=0.5 s时在第一台直驱风电机组处施加Δudcref=0.01 pu的阶跃扰动，前后时域仿真波形基本吻合，虽然降阶系统与全阶系统存在一定误差，但该误差处于标准范围内，且降阶系统与全阶系统在次同步频段内具有相同的运行效果，能够较好地等效全阶系统在次同步频段内的响应特性。

表3 为利用基于ADI 的平衡截断方法得到的降阶模型与全阶模型的对比。可以看出，利用基于ADI 的平衡截断方法得到的降阶模型，其计算次同步振荡模式和时域仿真的时间均远小于全阶模型，并且将模型阶数从1 200 阶降到6 阶；同时，利用ADI 迭代方法求解李亚普诺夫方程，有效缩短了仿真计算时间，提高了计算效率。

表3 降阶模型与全阶模型的比较Tab.3 Comparison between reduced order model and full order model

4 结论

利用基于ADI 的平衡截断方法，对直驱式永磁同步风电机组的风电场进行模型降阶研究，提出了面向直驱风电场次同步振荡分析的降阶模型，得到以下结论：

1）根据Hankel 奇异值以及全阶系统与风电场降阶系统Bode 图的吻合情况，与全阶模型相比，降阶模型将阶数从1 200阶降为6阶，同时在次同步频段内其响应与全阶模型基本相同。

2）选择合适的移位参数，利用ADI迭代的方法求解李亚普诺夫方程比传统方法的求解时间缩短了近1/3，提高了降阶速度。