堆栈式集成学习驱动的电力系统暂态稳定预防控制优化方法

潘晓杰，徐友平，解治军，王玉坤，张慕婕，石梦璇，马坤，胡伟*

（1.国家电网公司华中分部公司，湖北省 武汉市 430077；2.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机工程与应用电子技术系)，北京市 海淀区 100084）

0 引言

安全可靠的电力供应是国家发展和人民生活的重要保障。但是随着电力电子设备大量应用以及新能源并网容量增加，电力系统运行点日渐逼近稳定极限。暂态失稳是造成电力系统大规模事故的主要原因，有效的暂态稳定评估以及暂态稳定预防控制(transient stability preventive control，TSPC)方法，对于电力系统稳定运行具有重大意义[1-6]。

传统的暂态稳定评估方法主要包含时域仿真法、直接法和基于故障后系统响应的判断方法[7]三大类。这3 类方法具有计算准确、可行性强的优点，但是计算复杂、运算时间长和不适宜在线应用的缺点也很明显。随着机器学习方法在电力系统中的广泛应用，传统电力系统暂态稳定评估方法的弊端有了新的改善方案。文献[8]通过调整传统的支持向量机(support vector machine，SVM)得到保守型和激进型2种改进SVM模型，以此来解决电力系统中暂态稳定评估的结果难以保证保守性的问题。文献[9]根据不同电气特征对电力系统暂态稳定性的关联程度不同，利用人工神经网络(artificial neural network，ANN)构建了特征分离型暂态稳定智能评估模型。文献[10]结合模糊隶属函数和决策树(decision tree，DT)，构建了模糊规则暂态稳定评估分类器。但是现有的机器学习方法对输入特征的处理能力有限，在求解复杂分类问题时泛化能力易受到制约，因此并不能很好地实现电力系统暂态稳定评估[11]。随着新一代信息技术的快速发展，当前电力系统呈现海量数据的特征，基于深度学习方法的电力系统暂态稳定研究也越发深入[12-14]。文献[15]采用时域仿真与卷积神经网络(convolutional neural network，CNN)相结合的方法提高了暂态稳定评估的准确率。文献[16]提出了一种基于堆栈式自编码器(stacked autoencoder，SAE)的暂态稳定评估模型，该模型能够依靠深层结构挖掘数据的隐藏模式，提取出有利于暂态稳定评估的高阶特征。对于深度学习在电力系统暂态稳定评估中的应用，其面临的问题是多特征电气量信息挖掘能力有待提升，模型的泛化能力和准确性亟待提高。

暂态稳定预防控制是指系统在第一级标准规定的预想故障发生前，通过发电机出力调整、无功电压调整等措施，将系统调节到安全的运行方式下，从而保证系统在规定的预想故障发生后仍然可以稳定运行[17]。文献[18]提出了基于暂态稳定裕度对发电机出力进行灵敏度分析，从而确定断面功率和发电水平的方法；然而，电力系统是复杂的非线性动力系统，灵敏度法是对非线性方程的线性近似，应用于实际的复杂电力系统中计算效率低下。文献[19]提出了基于粒子群优化算法(particle swarm optimization，PSO)求解附加功角不等式约束的暂态稳定预防控制最优潮流模型；然而，面对大规模电网中复杂的模型约束，该方法的求解速度迅速下降，难以在合理的时间内得到有效的求解结果。文献[20]基于遗传算法(genetic algorithm，GA)优化的BP 网络生成暂态稳定评估器，并将其嵌入粒子群算法中，借以评估预防控制后的系统暂态稳定性；然而，该方法使用的反向传播神经网络(back propagation neural network,，BPNN)只有3层，难以拟合复杂的非线性方程。文献[21]使用二阶段SVM 进行暂态稳定评估，然而，如果只采用线性SVM求得的线性方程进行预防控制，将系统暂态稳定边界简单等效成一个高维平面，则模型相对简单，难以保证对大系统预防控制的准确性和策略的最优性。文献[22]采用拉丁超立方抽样法生成样本，使用深度置信网络(deep belief network，DBN)作为非显式暂态稳定约束，利用带精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ，NSGA-Ⅱ)求解预防控制优化模型；但是这一研究中所采用DBN网络对于暂态稳定样本的多样性特征挖掘能力不足，同时NSGA-Ⅱ是遗传算法的改进，寻优路径相对单一。

针对上述问题，本文提出了堆栈式集成学习驱动的电力系统暂态稳定预防控制优化方法，建立了基于堆栈式集成深度置信网络(stacking ensemble deep belief network，SEDBN)的暂态稳定评估模型。该模型依靠多层集成结构来强化弱分类器，将多个单独的分类器进行集成，所搭建的暂态稳定评估器具有多特征提取能力，以及更好的鲁棒性、泛化能力。与传统暂态稳定预防控制方法不同的是，该优化方法将训练后的暂态稳定评估器作为暂态稳定约束判别器，嵌入帝企鹅启发式优化(Aptenodytes Forsteri optimization，AFO)算法[23]的迭代寻优过程中，实现了预想故障集下以发电机组调控成本最小为目标的预防控制策略生成。

1 基于堆栈式集成DBN的暂态稳定评估器

1.1 堆栈式集成DBN

DBN是深度学习方法中的一种，其由多个受限玻尔兹曼机堆叠而成。虽然DBN具有强大的特征提取能力，但是单一DBN模型的最优结构确定和最优参数确定耗时费力，也存在结构不唯一的情况。因此，采用集成学习的方法融合多个DBN分类器，以弱化模型参数确定环节，同时能够获得更高的模型精度，并取得更强的鲁棒性和泛化能力。本文以DBN作为基础分类器单元，结合堆栈式集成学习的方法提升分类器性能。

集成学习方法是先基于不同样本特征训练多个子学习器，再采用一定的集成策略进行综合判断，输出最终结果，其本质是将弱分类器转化为强分类器的过程[24-25]。堆栈式集成DBN 分类器是一种多层的分类器结构，其本质是通过上层学习使底层多模型相结合，基本原理如图1所示。

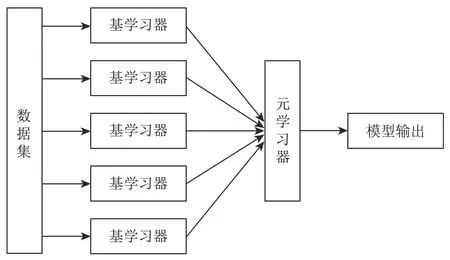
图1 堆栈式集成学习原理图Fig.1 Schematic diagram of stacked ensemble learning

底层的多个分类器为基分类器，上层的一个分类器为元分类器。堆栈式集成DBN是以多特征的有监督样本作为初始样本训练基分类器，再以底层的输出作为上层的输入特征，上层分类器输入数据的标签仍是初始样本标签。基于这样的堆栈式集成方法，可以降低分类误差，提高模型泛化能力。需要注意的是，堆栈式集成DBN方法在生成元分类输入特征时，应采用交叉验证法降低过拟合的风险。

1.2 暂态稳定评估器训练

1.2.1 暂态稳定系数

以系统暂态稳定系数(transient stability index，TSI)作为暂态稳定评估指标。TSI反映暂态过程中发电机最大功角差，表示为

式中δmax为系统中任意2台发电机之间的最大功角差。当ITS＞0 时，表示系统暂态稳定，并且ITS越大，系统暂态稳定性越高；当ITS＜0时，表示系统暂态失稳。本文设计的暂态稳定评估器的功能就是精确拟合多特征电气量与TSI 之间的关系，以此来代替暂态稳定约束的非线性微分代数方程组求解过程。

1.2.2 集成DBN模型的训练过程

堆栈式集成学习模型性能既受到样本数据的多样性影响，又与多个DBN模型基学习器的结构有关。因此，本文综合考虑不同特征子集与不同DBN 结构，构建集成学习模型作为暂态稳定评估器。

基学习器的输入设置为：特征集A为发电机有功出力，特征集B为节点电压幅值|V1|，|V2|，…，|Vm|，特征集C为节点电压相角θ1，θ2，…，θm，其中m和n分别为系统中节点总数和发电机总数，所有特征集样本的标签都基于PSASP 仿真软件计算TSI 所得。堆栈式集成学习是通过一个元分类器来整合多个分类模型的集成学习技术。基层子模型利用整个训练集进行训练，元模型将基层模型特征作为特征进行训练。集成DBN 的具体训练过程如下：将3 个特征集各自输入到3 个不同结构且性能优良的DBN 中，如图2所示，其结果按照均值法进行子模型输出集成，建立基学习器层；基学习器层将自身输出作为元学习器的输入特征，特征集的真实TSI 标签仍为元学习器的标签。经训练后，堆栈式集成DBN模型输出为ITS，当ITS＜0 时，认为电力系统暂态失稳，则在该发电机出力下，系统不满足暂态稳定约束，需进行预防控制，调整发电机出力。

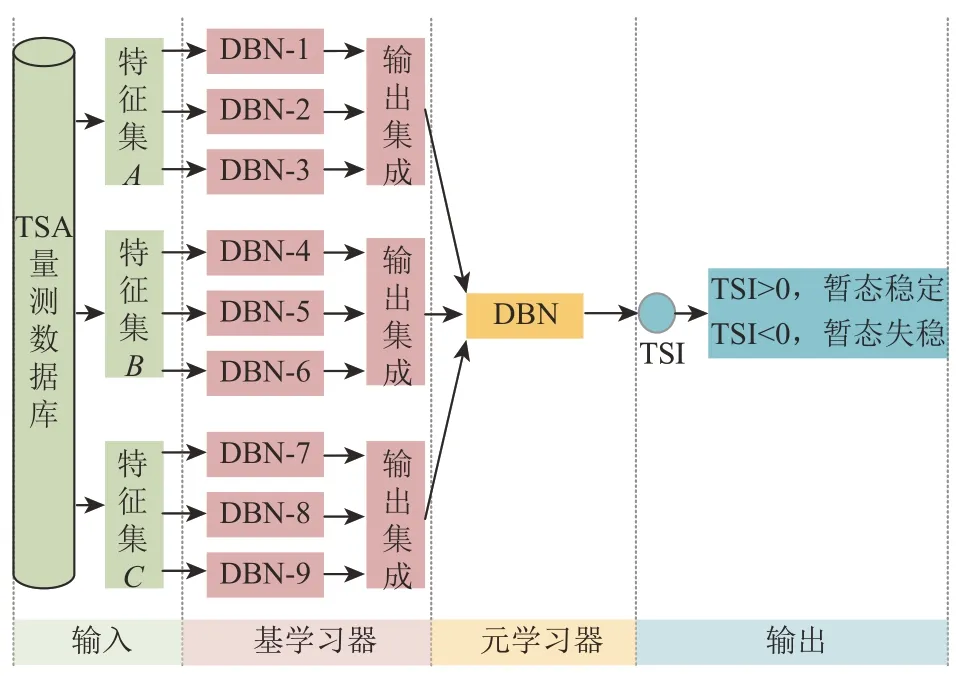
图2 基于堆栈式集成DBN的暂态稳定评估器模型Fig.2 Transient stability estimator model based on stacked ensemble DBN

2 堆栈式集成DBN驱动的电力系统暂态稳定预防控制算法

电力系统暂态稳定预防控制可以看作一个考虑暂态稳定约束的最优潮流(transient stability constrained optimal power flow，TSCOPF)模型。

2.1 电力系统暂态稳定预防控制

TSCOPF 以经济性最优及功角稳定为目标，在潮流平衡约束下，同时考虑功角暂态稳定性，最终找到稳态下最佳电力系统运行点，即发电机组出力情况。TSCOPF 具体目标函数及约束条件表示如下。

1）目标函数

预防控制手段采用发电机出力控制，以总调整成本最低为优化目标。目标函数表示为

式中：Cadjust为可控发电机组出力调整的总成本；SG为可调节发电机节点的集合；分别为第i台发电机预防控制前后各自的出力值；分别为第i台发电机节点的有功出力上调量和下调量；分别为第i台发电机出力上调、下调的调整成本。

2）网络潮流等式约束

在TSCOPF 模型中，网络潮流等式约束可以用负荷潮流等式来表示：

式中：Pi、Qi分别为注入母线i的有功功率和无功功率；V、δ分别为电压幅值和相角；|Vi|、δi分别为母线i的电压幅值和相角；δj为母线j的电压相角；|Yij|、ϕij分别为导纳矩阵值和相角；N为节点数。

电网运行的不等式约束包含发电机出力约束(8)、节点电压约束(9)和线路热稳约束(10)：

4）暂态稳定约束

电力系统的暂态稳定约束可以由一个微分方程(11)和一个代数方程(12)表示：

式中：x为状态变量；y为代数变量；λ为控制变量。

式(11)、(12)计算过程涉及非线性微分代数方程的求解，计算复杂且耗时长。在面对大电网所发生的众多故障时，方程计算复杂度极高，因此，设计便于求解及计算高效的暂态稳定约束判断方法，是电力系统暂态稳定预防控制的关键一环。

在具体求解过程中，可以使用MATPOWER对网络潮流约束和电网运行的不定式约束进行判断。但是暂态稳定约束(11)、(12)涉及非线性微分代数方程求解，传统求解方法计算难度大，耗时很长，因此，本文提出基于集成DBN的暂态稳定评估器，用以代替复杂求解过程。

颁奖典礼上，最大的主角还是来自全国各地的明星阿姨们。站在聚光灯下，阿姨们感情真挚的获奖感言，赢得了现场与会人员的阵阵掌声。听到宣读自己的名字，来自福建厦门的盛海霞兴奋不已。站在领奖台上，她激动地说“非常感谢兰心奖给我们阿姨一个展示自己的舞台。360行，行行出状元。今后，我对我从事的职业会更加感到自豪。我要用自己的案例告诉身边的朋友：一定要用心做事，甘于奉献。”

2.2 集成DBN驱动的AFO预防控制算法

将训练好的暂态稳定评估器嵌入到TSCOPF中，为高效求解TSCOPF，采用AFO 算法进行计算。该算法模拟帝企鹅种群取暖过程，基于帝企鹅取暖时移动的原则，即温度感知、参考记忆、最小化能量损耗、向种群中心移动、参考其他个体位置，设计启发式优化算法的优化求解方向，相比于传统的遗传算法，粒子群等优化算法具有计算复杂度低、求解速度快、收敛性好的优点。嵌入集成DBN的AFO结构如图3所示。

图3 SEDBN-AFO模型结构Fig.3 Model structure of SEDBN-AFO

在AFO 算法中嵌入MATPOWER 和基于堆栈式集成DBN 的暂态稳定评估器，构成SEDBNAFO 预防控制算法。首先，以可控发电机组整体出力情况作为企鹅种群，每只企鹅的位置和记忆代表每台可控发电机的有功出力；其次，使用MATPOWER 对当前种群位置下系统的网络潮流等式约束和电网运行的不等式约束进行判断，同时生成用于暂态稳定评估的节点电压幅值、相角特征；再次，将种群个体即发电机出力情况和节点电压幅值、相角输入到SEDBN暂态稳定评估器中，评估个体TSI，判断系统暂态稳定性；最后，AFO 算法根据约束条件判别情况，结合最小化调整成本优化目标进行TSCOPF 优化求解，得到企鹅种群位置移动策略，即发电机出力水平的调整量。暂态稳定预防控制算法流程如图4所示。

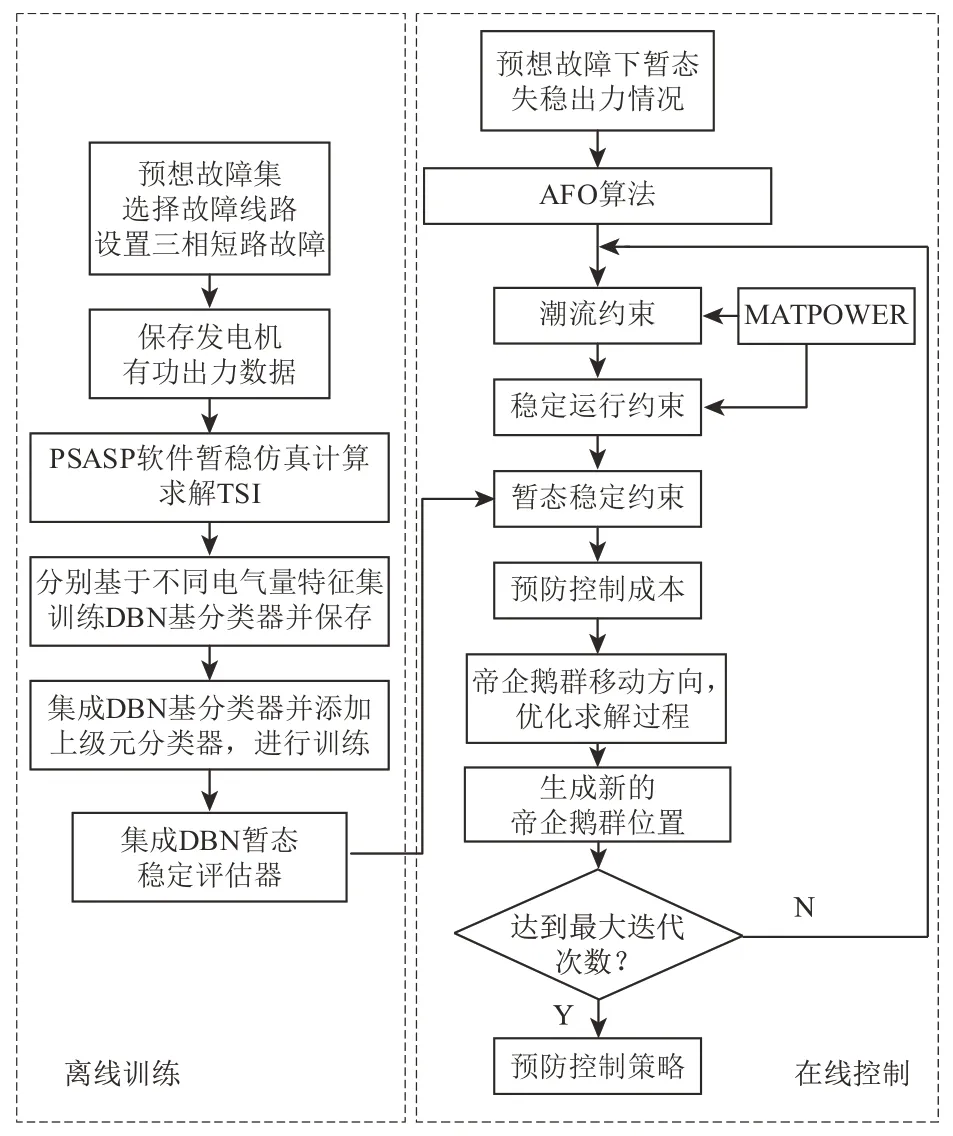
图4 暂态稳定预防控制算法计算流程图Fig.4 Calculation flow chart of transient stability preventive control algorithm

2.3 AFO算法改进

通过实验发现，在大多数情况下，AFO 算法中所用到的梯度估计策略的效率较低。为改进这一问题，本文采用高斯扰动的方法替代梯度估计策略，其表达式为

式中：xnew表示种群个体新位置；xc为扰动步长；xr1和xr2是种群中第r1、r2只企鹅的位置；Rn是一个服从正态分布的随机数矩阵；Dm是xc距离种群中所有企鹅位置的平均距离。

基于式(13)，更新种群中企鹅的新位置，继而迭代寻优，最终确定种群位置最佳分布，即发电机组最优出力。

3 算例分析

3.1 样本集构建及模型结构

以IEEE39 节点系统为算例，基于PSASP 软件进行数值仿真，生成样本数据，仿真采样频率设置为100 Hz，即采样时间步长为0.01 s。基于系统的基准发电水平，采用随机抽样方法在80%～120%发电水平范围内抽取5 000 种发电水平，并相应调整负荷水平(保存记录)，以保证系统功率平衡且各母线电压维持在0.95～1.05 pu范围内。故障设置为线路三相短路接地，经过一段时间后切除相应故障线路。为避免切除故障线路时系统出现孤岛现象，从46条线路中选择34条线路参与暂态故障扫描。各线路故障分别设置在每条线路长度的90%位置。故障开始时间设为t0=1 s，故障切除时间设为t1=1.10 s，仿真总时长为5 s，共生成170 000 个样本。针对同一发电水平下34 条线路的故障样本，计算出各自的TSI 值，从中筛选最小TSI值作为当前发电水平下的暂态稳定标签值，由此得到5 000个有标签训练样本，其中稳定样本有2 812个，失稳样本有2 188个，随机抽取4 000个样本组成训练集，剩余1 000 个样本组成测试集，以模型的整体识别准确率作为评价指标。基于图2 结构建立集成DBN 模型，具体模型参数如表1所示。

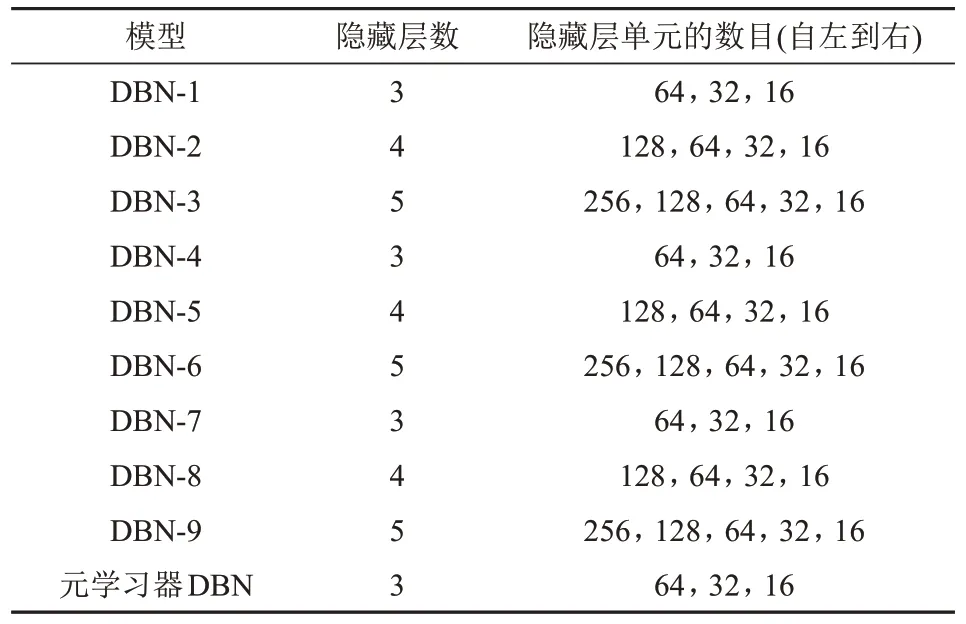
表1 堆栈式集成DBN模型结构参数Tab.1 Structure parameters of stacked ensemble DBN model

3.2 暂态稳定评估器训练及性能分析

3.2.1 集成模型性能分析

以10 机39 节点系统为测试系统，对集成DBN暂态稳定评估器进行训练，记录每次迭代训练的准确率和损失值，统计结果如图5 所示。可以看出，集成DBN模型收敛速度快且评估结果准确率高。

图5 暂态稳定评估器性能指标结果Fig.5 Performance index results of transient stability evaluator

为验证本文所提方法的优越性，基于相同样本集训练SAE、CNN 的深度学习模型，以及SVM、随机森林(random forest，RF)的浅层机器学习模型，并将其与集成DBN模型进行对比。各模型准确率结果如表2所示。

表2 不同模型性能对比Tab.2 Performance comparison of different models

从表2 可以看出，浅层机器学习方法(RF、SVM)的模型性能不佳，这是由于其模型结构简单，特征学习能力有限；深度学习方法(SAE、CNN)的模型性能优于浅层机器学习模型，这是由于其深层网络结构可以有效挖掘数据潜在规律；集成DBN能进一步提升模型性能，从而获得更高的模型精度。

3.2.2 堆栈式集成DBN 模型与子模型性能对比分析

为了验证堆栈式集成DBN 模型的性能优势，将各子分类器与集成学习评估器的暂态稳定评估准确率进行对比。为显示算法平均性能，重复3次10折交叉验证，并以箱型图来显示各子模型和集成模型的性能，结果如图6 所示。可以看出，堆栈式集成DBN模型的均值和中位数均高于其他单个子模型，性能最优，表明集成DBN模型在单个DBN模型性能基础上有所提升。

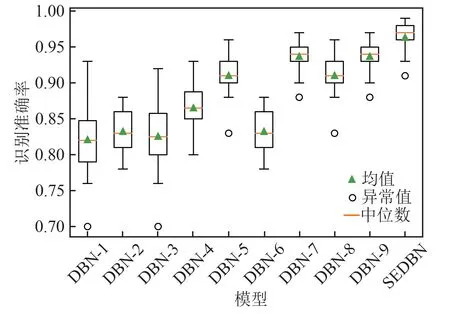
图6 堆栈式集成DBN暂态稳定评估器与各子评估器性能对比Fig.6 Performance comparison of stacked ensemble DBN transient stability estimator and each sub-estimator

3.3 AFO算法适应度分析

嵌入堆栈式集成DBN 的AFO 暂态稳定预防控制模型的性能可以用适应度曲线来表示，为了进一步验证AFO算法的优越性，分别采用AFO算法、遗传算法和粒子群算法进行对比实验，并记录求解过程中各模型的适应度值，如图7所示。

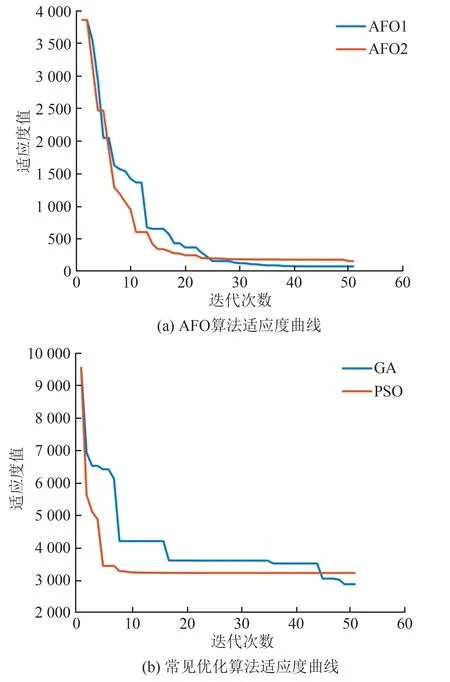
图7 不同模型适应度对比结果Fig.7 Fitness comparison results of different models

从图7(a)可以看出，改进的AFO2算法比原始的AFO1 算法收敛速度快。通过对比图7 可以看出，PSO 和GA 的适应度值最终收敛到3 000 左右，而AFO 算法的适应度值则收敛到接近于0，其优化效果更好。由此可见，AFO 算法比GA、PSO 算法的求解结果具有更好的适应度值，且寻优速度相对较快，具有较好的适用性和通用性，满足在线预防控制的要求。

3.4 结果分析

将基于堆栈式集成DBN的暂态稳定评估器嵌入AFO算法中，对暂态失稳发电机出力情况进行暂态稳定预防控制。39节点系统预防控制前后发电机出力对比如图8 所示，暂态稳定预防控制调节成本如表3所示。

表3 暂态稳定预防控制成本Tab.3 Transient stability prevention and control cost

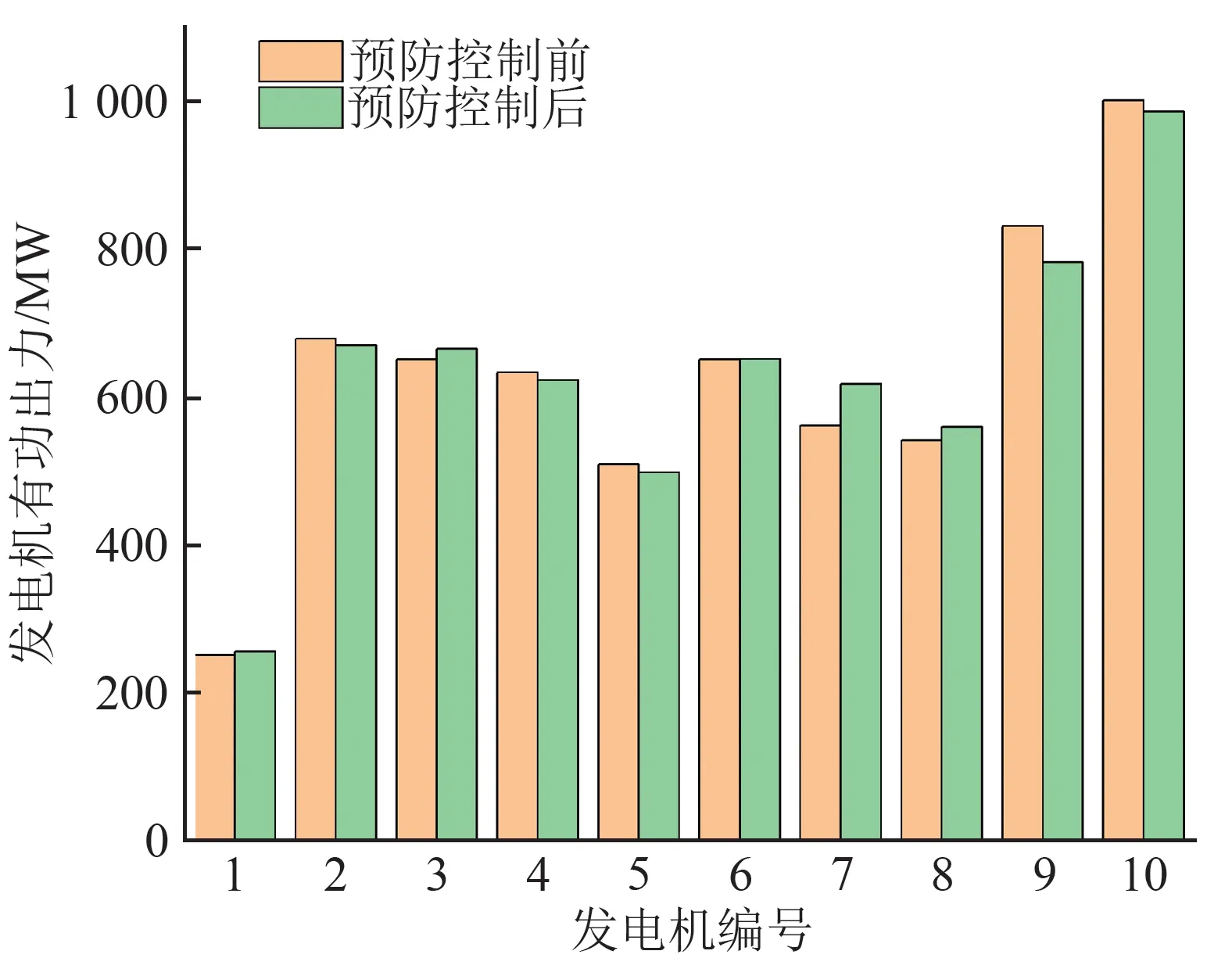
图8 系统预防控制前后发电机出力对比Fig.8 Comparison of generator output before and after system preventive control

使用PSASP 软件对预防控制策略进行验证，采用时域仿真法进行分析，选取2 个预想故障下预防控制前后发电机功角曲线进行对比。当BUS4与BUS3 相连的线路末端发生故障时，发电机功角曲线摆开情况及预防控制后的功角曲线如图9所示。当BUS28与BUS29相连的线路末端发生故障时，发电机功角曲线摆开情况及预防控制后的功角曲线如图10所示。

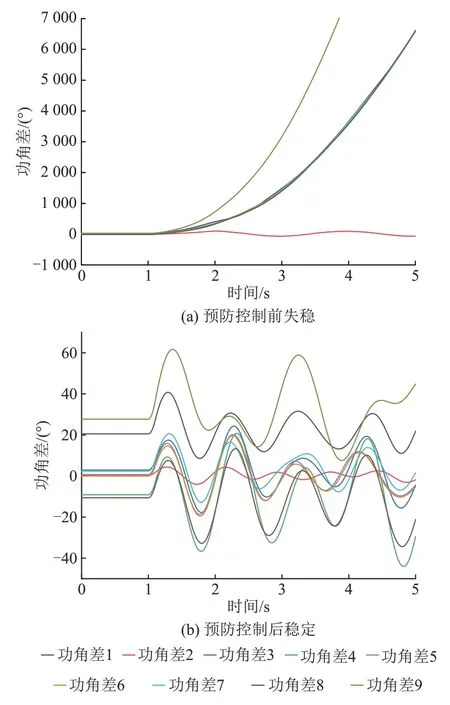
图9 BUS4与BUS3相连的线路故障采取预防控制前后发电机功角曲线对比Fig.9 Comparison of power angle curves of generators before and after preventive control of BUS4 and BUS3

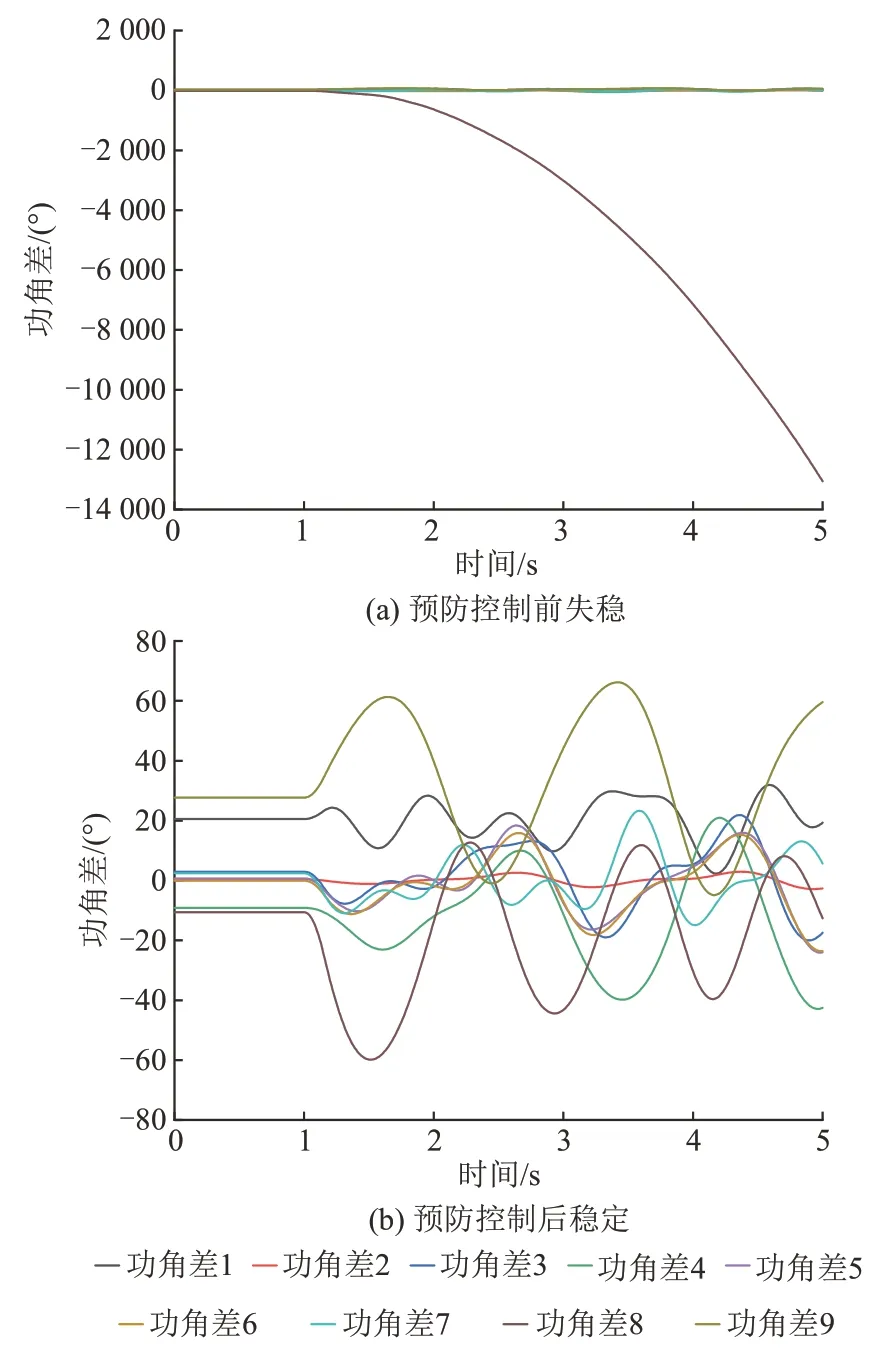
图10 BUS28与BUS29相连的线路故障采取预防控制前后发电机功角曲线对比Fig.10 Comparison of power angle curves of generators before and after preventive control of BUS28 and BUS29

从图9、10可以看出，采用预防控制可使系统从暂态失稳回归暂态稳定。由此可见，集成DBN驱动的电力系统暂态稳定预防控制启发式算法能够在电力系统正常运行时，通过发电机出力控制来保证电网充裕性和安全性。

4 结论

提出一种堆栈式集成学习驱动的电力系统暂态稳定预防控制优化方法，通过理论分析及实验研究，得到以下结论：

1）所建立的集成DBN 暂态稳定评估模型收敛速度快且评估结果准确率高。相较于传统的机器学习模型，集成DBN模型具有更好的性能和更高的精度。同时，集成学习结合多个不同输入特征和不同结构的子模型，有利于挖掘样本中的多样化特征。

2）所采用的AFO 算法具有多样化的寻优路径，与常见的群体智能优化算法相比，其求解结果收敛性更好，且寻优速度相对较快，满足在线预防控制的要求。

3）所提出的集成DBN 驱动的电力系统暂态稳定预防控制算法能够在电力系统正常运行时，通过对发电机出力进行预防控制来保证电网充裕性和安全性。