Ⅲ组合型线变截面涡旋齿的参数分析和优化
彭 斌, 陶耀辉, 刘慧鑫
(兰州理工大学 机电工程学院, 甘肃 兰州 730050)
涡旋压缩机作为先进容积式压缩机,具有运行平稳、低振微噪、节能高效等诸多优点,因而被广泛应用于工业、农业、医疗等需要压缩空气的领域.相较于等截面压缩机,变截面涡旋压缩机在压缩比和气体泄漏量方面都更为优秀,因而常常成为研究的热点.涡旋盘作为涡旋压缩机的核心零部件,其型线的优化设计便成为了其中的研究重点.
Shaffer等[1]基于控制体积法建立了变壁厚涡旋压缩机的几何模型.Liu等[2]运用有限元分析法对变径基圆渐开线涡旋齿进行了优化.彭斌等[3]建立了由圆渐开线、高次曲线、圆弧组合而成的变截面涡旋型线,构建了整体数学模型并进行了实验研究.侯才生等[4]基于Frenet标架建立了由圆渐开线和三次曲线构成的变截面涡旋型线,并在几何性能和动力性能方面与等截面涡旋型线进行了比较.张朋成等[5]利用不同极径的代数螺线生成了变截面涡旋齿,并与圆渐开线涡旋模型作了定量对比.李雪琴等[6]提出了非对称变壁厚涡旋齿结构,并在应力和变形方面与对称变壁厚涡旋齿进行了对比.Cavazzini等[7]利用PSO算法对涡旋压缩机的效率进行了优化研究.彭斌等[8]采用多目标遗传算法对双圆弧修正和双圆弧加直线修正中各参数不同组合的选取进行了优化.刘涛等[9]利用NSGA-Ⅱ算法对变截面涡旋盘几何性能和力学性能进行了综合优化.彭斌等[10]对变壁厚涡旋膨胀机的型线参数做了深入研究.张贤明等[11]结合NSGA-Ⅱ算法对涡旋压缩机动静涡旋齿受到的气体力、力矩和能效比进行了多目标优化设计,有效提高了涡旋压缩机的性能.
综上所述,对变截面涡旋压缩机研究主要集中于涡旋型线的设计和数学模型的建立等方面,而在型线参数的优化设计方面研究较少.本文引入Ⅲ(圆渐开线-圆渐开线-圆渐开线)变截面涡旋齿的型线面积、占积比和行程容积模型,利用控制变量法研究Ⅲ变截面涡旋齿的型线参数对型线面积、占积比和行程容积的影响,并利用NSGA-Ⅱ算法进行多目标优化设计,研究结果可为Ⅲ变截面涡旋齿的设计提供一定参考.
1 型线母线的建立
组合型线母线由3段圆渐开线组成,其中,第1段和第3段圆渐开线的基圆半径相同,第2段圆渐开线的基圆半径要比其他2段的基圆半径大.渐开线母线方程如下:
第1段圆渐开线母线方程为
(1)
第2段圆渐开线母线方程为
(2)
第3段圆渐开线母线方程为
(3)
为保证型线的连续性和光滑性,曲率半径需满足的条件为
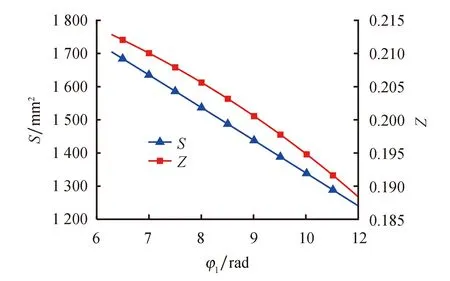
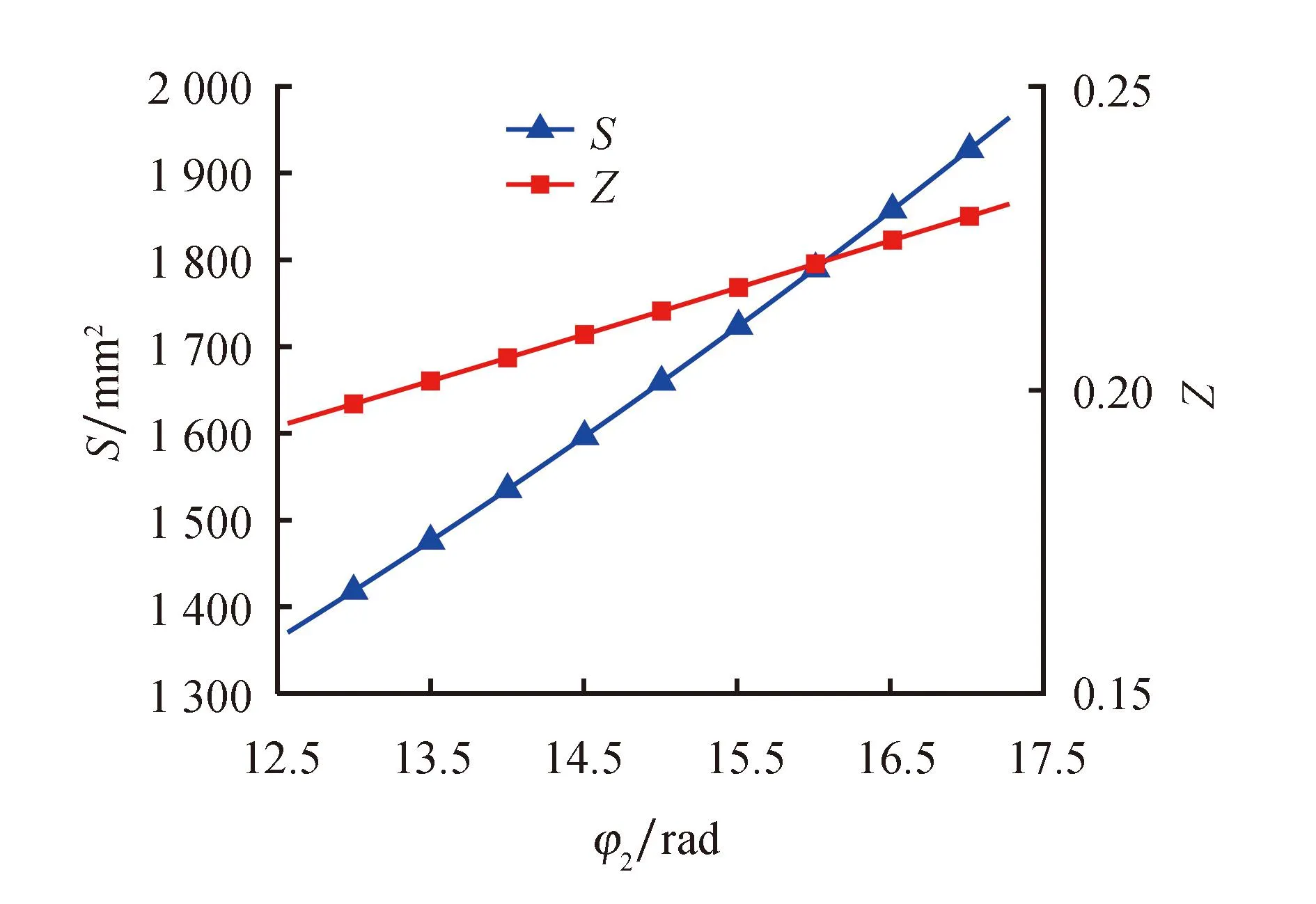
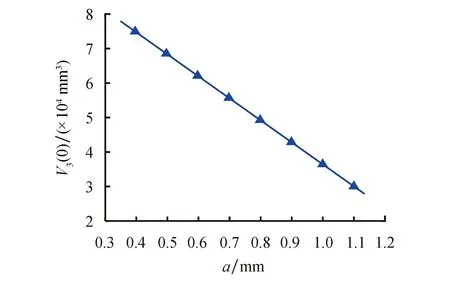
式中:φ1为第1段圆渐开线最大展角;φ2为第2段圆渐开线最大展角;φe为渐开线终端展角;a为第1段和第3段圆渐开线基圆半径;a1为第2段圆渐开线基圆半径,且a 利用法向等距线法[12]由母线生成Ⅲ变截面涡旋齿,并对变截面涡旋齿齿头进行双圆弧修正,得到修正后的变截面涡旋齿如图1所示. 图1 Ⅲ变截面涡旋齿Fig.1 Ⅲ variable wall thickness scroll tooth 涡旋齿的型线面积由涡旋齿外壁型线与基圆所围面积减去内壁型线与基圆所围面积而得,内、外壁型线如图2所示. 图2 涡旋齿内、外壁型线Fig.2 Inner and outer profile of scroll tooth 圆渐开线面积增量为 (7) 其中, (8) dL=ldφ=a(t-α)dφ (9) 式中:α为渐开线发生角;t为渐开线结束角. 则面积增量为 (10) 涡旋齿齿头采用双圆弧修正,双圆弧修正面积为 (11) 式中:Rd为修正大圆弧半径;Rx为修正小圆弧半径;γ为修正角;θ为主轴转角. 由此可得,Ⅲ变截面内、外壁型线与基圆所围面积和涡旋齿型线面积So、Si、S分别为 式中:So1、So2、So3分别为涡旋齿外壁的第1段、第2段、第3段圆渐开线与基圆所围面积;Si1、Si2、Si3分别为涡旋齿内壁的第1段、第2段、第3段圆渐开线与基圆所围面积. 涡旋型线占积比是涡旋齿的型线面积占涡旋盘总面积的比值.在涡旋盘盘径一定的条件下,型线面积越小占积比就越小,涡旋盘的有效容积就越大,同时材料利用率就越高.Ⅲ变截面涡旋齿的占积比Z为 Z=S/Sp (15) 式中:Sp为涡旋盘总面积,即 Sp=πR2 (16) 式中:R为涡旋盘半径,即 (17) 式中:Ror为涡旋盘回转半径. 当主轴转角θ=0时,涡旋盘压缩腔闭合,最外圈压缩腔的容积为行程容积. 最外圈压缩腔母线长度为 (18) 式中:x′2和y′2为式(2)的一阶导数;x′3和y′3为式(3)的一阶导数. 最外圈单个压缩腔面积为 A3(θ)=2Ror[L3+Rt(φe-2π)-Rt(φe)] (19) 式中:Rt为渐开线展角处对应基圆半径. 行程容积为 V3(0)=2A3(0)h (20) 式中:h为涡旋齿齿高. 由式(14,15,20)可知,Ⅲ变截面涡旋齿的型线面积、占积比和行程容积都与基圆半径a、渐开线发生角α、渐开线展角φ1、φ2和终端展角φe有关. 基圆半径a对型线面积和占积比的影响如图3所示.由图3a可以看出,当基圆半径a从1 mm增加到3 mm时,变截面涡旋齿型线面积和圆渐开线涡旋齿型线面积都是逐渐增加的,且变截面涡旋齿的型线面积明显大于圆渐开线涡旋齿的,而圆渐开线涡旋齿型线面积的增加速率明显大于变截面涡旋齿的. 由图3b可以看出,基圆半径a对变截面涡旋齿占积比的影响与对型线面积的影响正好相反,变截面涡旋齿占积比随a的增加逐渐减小,而圆渐开线涡旋齿占积比不随a的增加而改变.这是因为当a改变时,圆渐开线涡旋盘总面积的变化速率与型线面积的变化速率相同,而变截面涡旋盘总面积的变化速率大于型线面积的变化速率,从而导致变截面涡旋盘的占积比逐渐减小,圆渐开线涡旋盘占积比不变.当基圆半径a增加到2.62 mm时,变截面涡旋盘的占积比与圆渐开线涡旋盘的占积比相同. 图3 基圆半径对型线面积和占积比的影响 因此,在设计Ⅲ变截面涡旋盘时,若考虑基圆半径对占积比的影响,可以在满足a 终端展角φe对型线面积和占积比的影响如图4所示.由图4a可以看出,当终端展角φe从17.28 rad增加到20.42 rad时,变截面涡旋齿和圆渐开线涡旋齿的型线面积近似为线性增加,其中,变截面涡旋齿型线面积的增加速率较大. 由图4b可以看出,终端展角φe对变截面涡旋齿和圆渐开线涡旋齿占积比的影响完全相反,变截面涡旋齿占积比随φe逐渐减小,而圆渐开线涡旋齿占积比随φe逐渐增大.这是因为变截面涡旋盘总面积随φe的变化速率大于涡旋齿型线面积随φe的变化速率,从而导致型线面积增加的同时涡旋盘总面积增加得更快;而圆渐开线涡旋齿型线面积随φe的变化速率大于涡旋盘总面积随φe的变化速率,从而导致涡旋齿型线面积和涡旋盘总面积都增加的同时占积比也在增大. 图4 终端展角对型线面积和占积比的影响 因此,在设计Ⅲ变截面涡旋盘时,若考虑终端展角对占积比的影响,可以在满足相关设计要求的同时选择较小的终端展角,使得Ⅲ变截面涡旋盘的占积比较小. 渐开线展角φ1、φ2对变截面涡旋齿型线面积和占积比的影响分别如图5和图6所示.可以看出,型线面积和占积比随φ1的增加而减小,随φ2的增加而增大. 图5 渐开线展角φ1对型线面积和占积比的影响Fig.5 Influence of involute spread angle φ1 on profile area and occupancy ratio 图6 渐开线展角φ2对型线面积和占积比的影响Fig.6 Influence of involute spread angle φ2 on profile area and occupancy ratio 因此,在设计Ⅲ变截面涡旋盘时,若考虑渐开线展角对占积比的影响,可以在满足涡旋盘设计要求的同时选取较大的φ1和较小的φ2,使得Ⅲ变截面涡旋盘的占积比较小. 发生角与型线面积和占积比的关系如图7所示.可以看出,当发生角从0.34 rad增加到1.13 rad时,发生角与型线面积和占积比都呈正相关.同时,对比图5和图6可以看出,发生角对占积比的影响非常显著.因此,通过改变发生角的大小可以有效改善涡旋盘的占积比. 图7 发生角对型线面积和占积比的影响Fig.7 Influence of occurrence angle on profile area and occupancy ratio 基圆半径和发生角对的变截面涡旋盘行程容积的影响如图8和图9所示.可以看出,基圆半径和发生角对行程容积的影响完全相反,行程容积随基圆半径的增加而增大,随发生角的增加而减小.因此,可以通过对基圆半径和发生角的优化寻求行程容积的最优解集. 图8 基圆半径对行程容积的影响Fig.8 Influence of base circle radius on suction volume 图9 发生角对行程容积的影响 NSGA-Ⅱ算法是以遗传算法为基础并通过Pareto最优概念得到具有精英策略的快速非支配排序遗传算法.首先,NSGA-Ⅱ算法通过随机产生的初始种群,经过非支配排序后进行选择、交叉、变异的操作生成第1代子种群.然后,将父代种群与子代种群合并为新种群,并通过快速非支配排序、计算拥挤度、精英策略等操作生成新的父代种群.最后,通过对生成的父代种群进行选择、交叉、变异的操作生成新的子代种群.以此类推,直到算法满足最大进化代数,得到Pareto最优解集. 本文引入Ⅲ变截面涡旋齿的占积比和行程容积作为涡旋盘几何性能的评估对象,从而将占积比和行程容积确定为优化目标.由于优化目标有多个型线参数共同影响,所以优化变量选择了相互独立且对变截面涡旋盘性能影响相反的型线参数,即基圆半径a和发生角α.由占积比和行程容积的定义可以确定约束条件为V3(0)>0和0 4.2.1基圆半径的优化 由图3和图8可以看出,Ⅲ变截面涡旋齿的占积比随基圆半径的增加而减小,行程容积随基圆半径的增加而增大.两优化目标随优化变量的变化趋势相反,即两优化目标无法同时取得极值.因此,考虑对其进行多目标单初始参数优化,取得基圆半径的Pareto最优解集. 图10是对占积比和行程容积通过NSGA-Ⅱ算法进行单初始参数优化的结果.可以看出,两优化目标随优化变量的改变呈相反的变化趋势,这对应于基圆半径与占积比和行程容积的关系,证明了优化结果的合理性.选取部分Pareto最优解集,如表1所列.由上文可知,随着基圆半径的改变,两优化目标的取值不能同时达到最优,而表1中基圆半径的取值是经过NSGA-Ⅱ算法优化后并且考虑了占积比和行程容积取值的Pareto最优解. 图10 优化基圆半径Fig.10 Optimize the base circle radius 表1 基圆半径的Pareto解集 4.2.2发生角的优化 同理,由于发生角对占积比和行程容积的影响是相反的,所以利用NSGA-Ⅱ算法对发生角也进行多目标单初始参数优化,结果如图11所示,Pareto解集如表2所列. 图11 优化发生角Fig.11 Optimize occurrence angle 由于基圆半径和发生角对变截面涡旋齿占积比和行程容积的影响都是相反的,所以利用NSGA-Ⅱ算法进行多目标多初始参数优化,得到相关型线参数的Pareto最优解集. 图12是对占积比和行程容积通过NSGA-Ⅱ算法进行多初始参数优化的结果.可以看出,相比单初始参数优化,经多初始参数优化后占积比和行程容积的取值范围更大.因此,通过多初始参数优化可以选取更好的优化参数,从而生成变截面涡旋盘. 图12 优化基圆半径和发生角Fig.12 Optimize base circle radius and occurrence angle 选取优化后部分Pareto最优解集,如表3所列.由上文可知,随着基圆半径和发生角的改变,两优化目标的取值不能同时达到最优,而表3中基圆半径和发生角的取值是经过NSGA-Ⅱ算法优化后并且考虑了占积比和行程容积取值的Pareto最优解. 表3 基圆半径和发生角的Pareto解集 在多目标多初始参数优化后的Pareto最优解集中选取1组最优解集,即a=1.717 8 mm和α=0.353 rad,生成优化后的变截面涡旋盘如图13所示.同时,将优化后涡旋盘与优化前涡旋盘的占积比、行程容积和开始排气角处的轴向气体力Fa进行对比,对比结果如表4所列. 由表4可以看出,优化后涡旋盘在几何性能方面有了明显提高,优化后涡旋盘行程容积提升了5.49%,占积比降低了23.81%.由此说明,通过NSGA-Ⅱ算法可以有效改善Ⅲ变截面涡旋盘的几何性能.但是通过对比也可以发现,优化后涡旋盘在开始排气角处的轴向气体力增加了30.84%,对涡旋盘的力学性能不利. 图13 优化后涡旋齿Fig.13 The optimized scroll tooth 表4 涡旋盘对比 本文建立了Ⅲ组合型线变截面涡旋齿型线面积、占积比和行程容积的数学模型,得到了渐开线发生角、基圆半径、渐开线展角和终端展角随数学模型的变化规律.可以发现,与圆渐开线涡旋齿相比,Ⅲ变截面涡旋齿在型线面积和占积比方面性能较差. 结合占积比和行程容积,利用NSGA-Ⅱ算法对型线参数进行了优化.结果表明,Ⅲ变截面涡旋齿的行程容积提升了5.49%,占积比降低了23.81%,轴向气体力增加了30.84%,几何性能提升的同时力学性能有所下降.因此,设计Ⅲ变截面涡旋齿时,在满足力学性能要求的条件下,可以通过NSGA-Ⅱ算法优化选取合适的型线参数,从而提高涡旋齿的几何性能.
2 数学模型的建立
2.1 型线面积


2.2 占积比
2.3 行程容积
3 型线参数对数学模型的影响
3.1 基圆半径对型线面积和占积比的影响

3.2 终端展角对型线面积和占积比的影响

3.3 渐开线展角对型线面积和占积比的影响
3.4 发生角对型线面积和占积比的影响

3.5 基圆半径和发生角对行程容积的影响

4 NSGA-Ⅱ算法的优化
4.1 优化目标、优化变量和约束条件的确定
4.2 单初始参数的优化



4.3 多初始参数的优化


5 涡旋盘对比


6 结论

