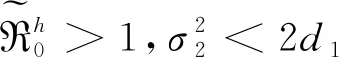一类具有饱和发生率的染病食饵-捕食者随机模型的动力学分析

赵玉凤

( 山西工商学院 计算机信息工程学院, 太原 030000 )

0 引言

由于HollingⅢ型功能反应函数更适合于描述脊椎动物种群随时间的变化规律,因此一些学者对HollingⅢ型功能反应函数的捕食模型进行了研究[1-3].在捕食者-食饵模型中,由于捕食者的平均生长率需要考虑食饵丰度与捕食者丰度的比值,因此一些学者进而研究了具有比例依赖的功能反应的食饵-捕食者模型[4-5].为了解不同生态系统的动力学性质,学者们利用It公式、大数定律、鞅理论分析了不同系统的动力学性质,其中包括全局正解的存在唯一性、遍历平稳分布的存在性、灭绝性和持久性、周期解等[4-8].文献[9]的研究表明,饱和发生率通常比双线性发生率(bX1X2)更适合于描述某些流行病的传播.基于上述研究,本文提出了一类带有饱和发生率和比率依赖的HollingⅢ型功能反应的染病食饵-捕食者模型:

(1)

考虑到环境噪声会对生物学系统产生不可忽略的影响,因此本文对系统(1)进行了线性扰动,以此建立了一个如下具有饱和发生率和logistic增长的随机模型(式(2)),并对其动力学性质进行了研究.

(2)

式中:{Bi}t≥0(i= 1,2,3)是相互独立的标准布朗运动.

1 全局正解的存在性和唯一性

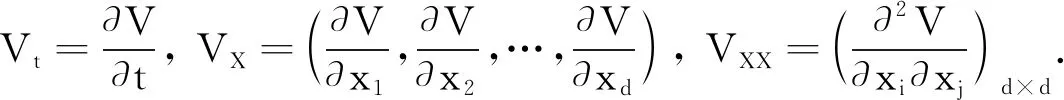
设X(t)∈Rn,则Lyapunov函数V的It公式为dV(X(t),t)=LV(X(t),t)dt+VX(X(t),t)g(X(t),t)dB(t).

证明由于定理1的证明过程与文献[4]中定理2.1的证明过程相似,故省略.

2 平稳分布的遍历性

引理1(Has’miniskii)[10]设有界域D⊂Rd,且其边界是正则的,若:

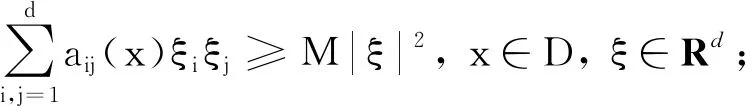
2)存在一个非负C2-函数V,使得对于任意的RdD,LV是负的,

则系统(2)中的马尔可夫过程X(t)有一个遍历平稳分布μ(·).

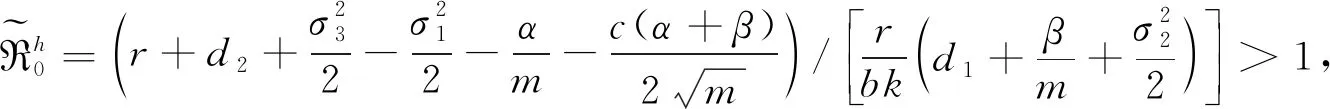
证明由扩散矩阵的计算公式得系统(2)的扩散矩阵为:

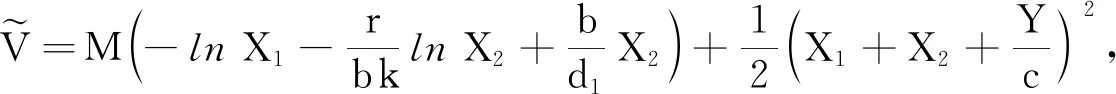
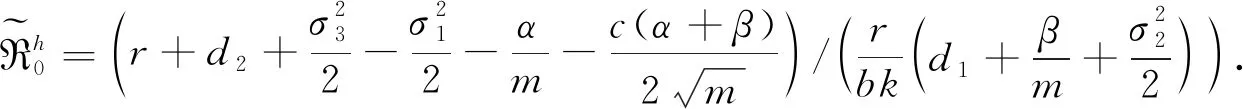
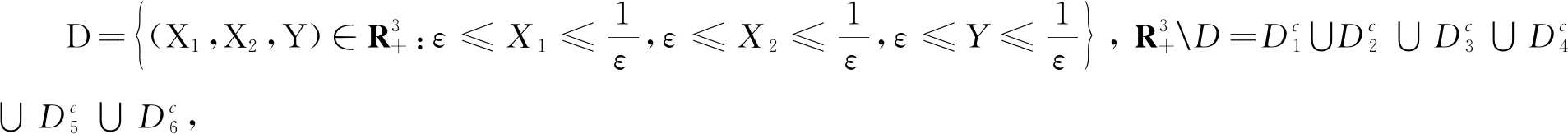
(4)

(6)

(7)

(8)

(9)

(10)

其中:

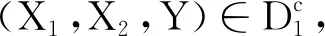
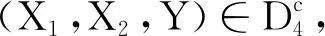
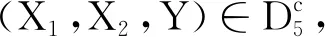
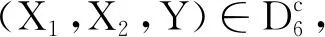
由上述讨论和引理1可得,系统(2)存在一个平稳分布,定理2得证.

3 灭绝性和持久性

引理2[11]设X(t)∈C(ΩX[0,∞),R+),则有:

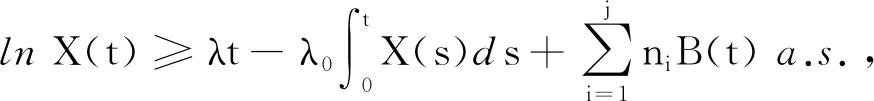
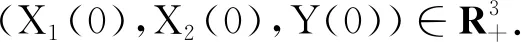
证明对lnX1利用It公式可得:

(11)

对式(11)从0到t进行积分后再除以t可得:

类似地,对lnX2利用It公式可得:

(12)

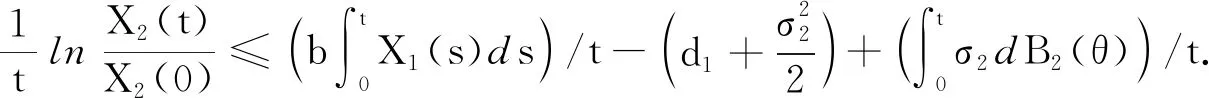
类似地,对lnY利用It公式可得:

(13)

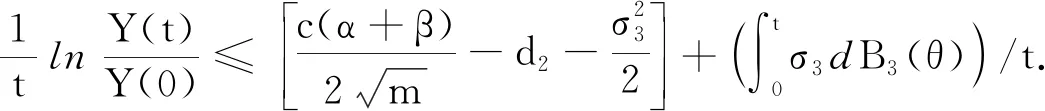
(14)

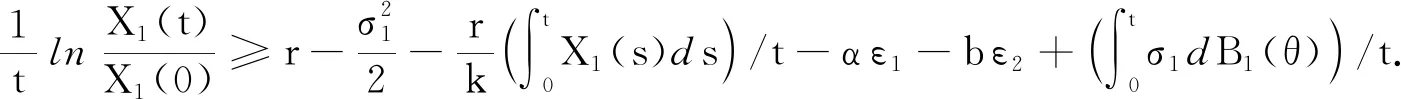
证明对lnX2利用It公式可得再由定理3可知,存在任意小的常数ε1(ε1>0)和ε2(ε2>0),使得当t>T时有和X2<ε2.由此可得:对该式从0到t进行积分后再除以t可得:

4 数值模拟

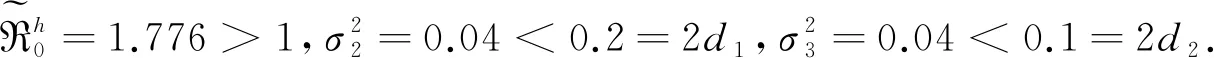
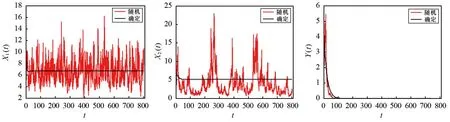
图1 在噪声强度为σ1=σ2=σ3= 0.2,初始值为X1(0)= 10、X2(0)= 6、Y(0)= 4时系统(2)的解X1(t)、X2(t)、Y(t)的路径图

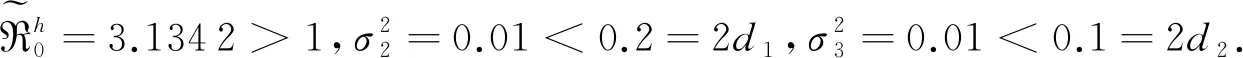
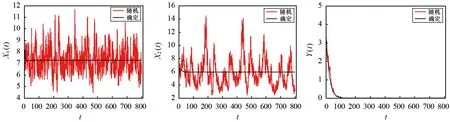
图2 在噪声强度为σ1=σ2=σ3= 0.1,初始值为X1(0)= 10、X2(0)= 6、Y(0)= 4时系统(2)的解X1(t)、X2(t)、Y(t)的路径图

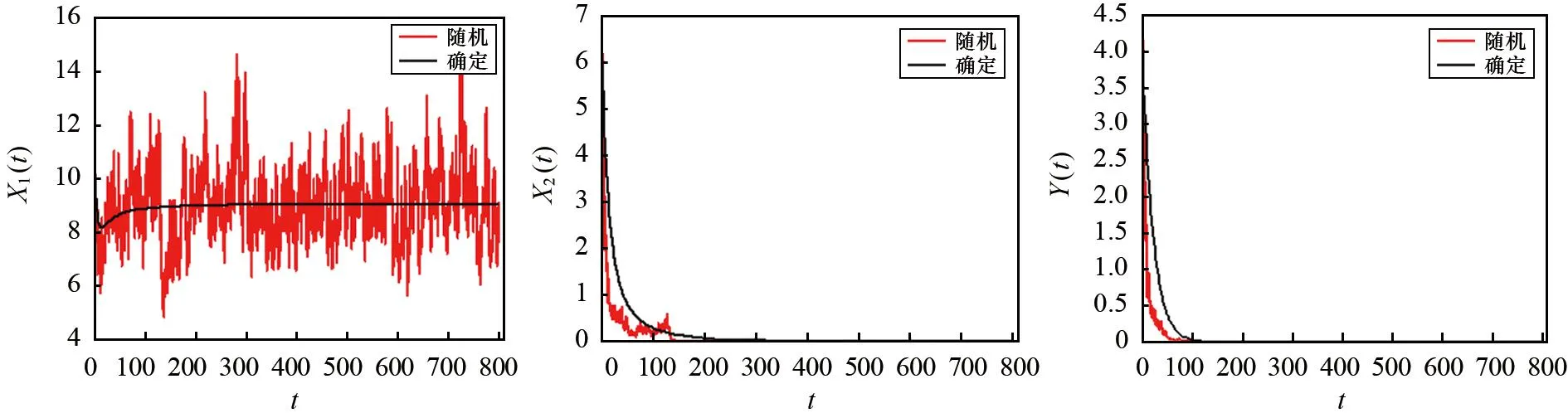
图3 在噪声强度为σ1= 0.1、σ2=σ3= 0.2,初始值为X1(0)= 10、X2(0)= 6、Y(0)= 4时系统(2)的解X1(t)、X2(t)、Y(t)的路径图

5 结论