TSN 中基于链路负载均衡的AVB 流量带宽分配方法

陆以勤 熊欣 王猛 覃健诚 潘伟锵

（华南理工大学 电子与信息学院，广东 广州 510640）

随着工业互联网的发展和各种新兴应用的产生，越来越多的行业领域都需要确定性低时延的网络连接，传统以太网缺少确定性传输机制，无法满足众多应用场景的需求。时间敏感网络（TSN）作为一种新兴的网络技术，能够保障网络流量的确定性低时延传输，在工业互联网、移动前传、车载网络等多个领域得到广泛的应用［1］。时间敏感网络工作组制定了一系列协议来保障时间敏感流量的确定性传输，包括IEEE 802.1AS［2］时间同步、IEEE 802.1Qbv［3］流量调度、IEEE 802.1Qav［4］队列及转发等。其 中IEEE 802.1Qav 协议定义了基于信用的整形（CBS）机制，用以传输音视频桥接（AVB）流量。为了防止流量的持续突发，CBS机制将数据的排队等待和传输发送与队列信用值的变化相关联［5］，而队列信用值的变化主要受逻辑带宽参数IdleSlope 的控制，IdleSlope 分配不当会影响AVB 流量的确定性传输。如果IdleSlope过小，流量就会在队列中排队等待信用值的恢复，从而造成过多的延迟；如果IdleSlope过大，则容易导致队列的信用值过大，增加流量的突发性，影响后级节点的传输。为了在有限的带宽资源下最大限度地保障AVB流量的传输性能，需要合理配置端口的逻辑带宽IdleSlope。

IEEE 802.1Qat［6］流预留协议（SRP）可以视为TSN中一个基础的带宽分配方案，通过协议信息交换的方式来预留带宽，但此方法从单条流量传输的需求来分配带宽，可能会导致流量变得不可调度［7］。Nam 等［8］提出了一种简单的SRP，但本质上也是从单条流量传输的需求出发。IEEE 802.1 Qcc［9］提出了集中式网络管理框架，实现了对SRP的增强，但该标准没有提供具体的实施规范。

在TSN 中，关键流量的传输总是与网络时延有关，带宽分配不当会影响流量的传输时延及网络的带宽利用率［10］，故部分研究将TSN的网络时延分析与带宽分配相结合，以实现网络的带宽分配。Cao等［11］定义了截止时间约束和链路负载率约束，以求解单个节点中基于CBS的预留带宽。为了对整个网络的带宽进行分配，赵长啸等［12］基于网络演算［13-14］的方法构建端到端时延分析模型，并建立了约束条件和目标函数，采用启发式算法求解所有节点的带宽分配。Li等［15］提出了一种基于SDN的业务带宽分配框架，显著增强了实时网络通信期间的带宽预留管理。由于网络演算的悲观性，分析的时延上界往往会很差。为更加准确地刻画网络节点的最坏时延，Li等［16］提出了一种Shaper曲线，更加精细地刻画了网络中流量的到达曲线，使得时延分析结果更加精确，并由此得到更加优异的带宽分配方案。但上述基于网络演算的带宽分配方法存在两个主要问题：①未考虑路由和负载对AVB 流量可调度性的影响，当利用网络演算进行性能评估时，如果某个节点的流量超过节点的最大处理能力，会使得带宽分配无解，影响AVB流量的传输调度；②目前研究的实验网络都是单节点或者简单的工业控制网络，在大规模情况下无法快速求解出最优的带宽分配结果，影响AVB流量的传输性能及网络的带宽利用率。

基于上述研究工作，文中提出了一种基于链路负载均衡的AVB 流量带宽分配方法：首先采用链路负载均衡的路由算法平衡各链路AVB 流量的大小，由此获得网络中AVB流量的最优路径；然后，基于流量路径和网络演算理论，分析了AVB 流量的端到端最坏转发时延，从而建立带宽分配的优化目标和约束条件，并针对带宽分配求解问题对带宽参数配置进行了优化。最后，文中通过实验验证了该方法的有效性。

1 TSN整形机制

1.1 TSN流量整形

在典型的TSN交换机架构中，每个交换机输出端口至多有8 个优先级队列，可以传输至多8 种不同的优先级流量，其中至少有一个队列用以传输时间触发（TT）流量，剩下的队列可用以传输AVB 流量和尽力而为（BE）流量，通常AVB 流量包括A、B两个类别的流量，文中分别用AVB_A 和AVB_B表示，并且AVB_A 的优先级高于AVB_B。为了实现TSN中的混流传输，通常混合使用时间感知整形器（TAS）和CBS，TAS 通过门控列表对TT 流量进行精准调度［17］，而AVB 流量通过CBS 进行传输调度。为了保证TT 流量的确定性传输，在TT 流量传输时隙开始之前引入保护带（GB）。如图1 所示，在T0时隙，TT 流量所在的队列门被打开，其他队列处于关闭状态，因此TT 流量在该时隙内到达交换机可以立即被发送；在T1时隙，TT流量队列门关闭，其他队列门打开，因此AVB 和BE 流量可以进行传输；在T2保护带时隙，所有队列的门处于关闭状态，也就是在该时隙内不能进行新流量传输，在GB 开始之前传输的流量可以在此期间完成传输，因此当TT 流量到达交换机时可以不被阻塞而立即转发。

为了防止AVB流量的持续突发，CBS通过参数IdleSlope 和SendSlope 调节队列信用值，其中IdleSlope代表流量的信用增长速率，也代表该类流量所预留的逻辑带宽。考虑一个基于CBS进行流量传输的初始场景，队列信用值的变化如图2 所示，其中，AVB流量的传输主要遵循以下几条规则：

图2 CBS下流量传输与信用值变化示意图Fig.2 Schematic diagram of traffic transmission and credits change under CBS

（1）当AVB 数据帧到达队列时，如果此时有低优先级的数据帧传输，AVB 数据帧需要排队等待，并且队列的信用值会以IdleSlope的速率增长，待低优先级数据帧传输完成之后，AVB队列数据才开始传输，并且信用值会以SendSlope 的速率减小，而在GB以及TT窗口AVB流量的信用值保持不变。

（2）当队列数据帧传输完成之后，如果信用值小于0，则其会以IdleSlope 的速率增长至0；如果信用值大于0，则其会被置为0。

（3）仅当队列信用值大于等于0 时，该队列的数据帧才可以进行传输；当队列信用值小于0 时，不能开始数据帧的传输，但信用值减为0以前开始传输的数据帧可以继续传输。

式中，C为物理链路带宽，为信用增长速率

1.2 问题描述

CBS 机制通过调整队列的逻辑带宽IdleSlope来防止流量的持续突发，带宽分配不当会影响AVB流量的确定性传输性能。如果带宽分配不足（如图3所示），则AVB 流量会在队列中排队等待信用值的恢复，由于信用值的恢复时间过长，导致前一个周期的数据排队等到下一个周期才进行传输，这很容易引起流量的传输延迟，并且随着流量的累积，很容易引起帧的丢失［16］。

图3 带宽分配不足场景［16］Fig.3 Insufficient bandwidth scenario［16］

由于TSN中存在多种流量混合传输且总的传输带宽有限，所以给AVB流量预留尽可能多的带宽是不现实的。若预留的带宽过多（见图4），在流量排队等待的过程中，队列信用值会增长到较大值，等到干扰流量完成传输后，累积的流量就会持续突发，影响网络的整体传输性能。信用值的持续增长可能会导致信用值溢出，而AVB流量的信用值有界是分析AVB流量端到端最坏时延的前提，若信用值上界不断溢出，会使得该类流量的最坏时延无界［14］。

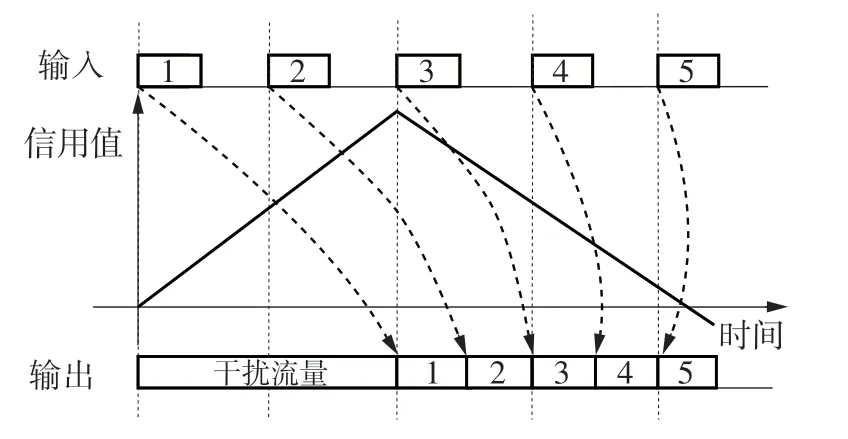
图4 带宽分配过多场景Fig.4 Excessive bandwidth scenario

随着工业4.0的发展以及5G背景下移动设备需求的变化，网络中还经常面临着重新配置的挑战，当网络动态变化时，往往需要重新计算带宽参数，这就对带宽分配求解有速度和质量的要求。而目前相关研究的实验网络都是单节点或者简单的工业控制网络，在网络规模较大时无法快速得到带宽最优解，影响流量的确定性传输。因此，如果可以快速地求解出最优的IdleSlope参数，实现流量最优带宽分配，就可以在有限带宽资源下更好地保障AVB流量的传输，提升网络的带宽利用率。

2 带宽分配方法

2.1 带宽分配流程

图5为文中带宽分配方法的流程图，输入为网络拓扑及流量信息，通过建立优化目标和约束条件，采用启发式算法求解出各端口的带宽分配结果，主要包括以下步骤：

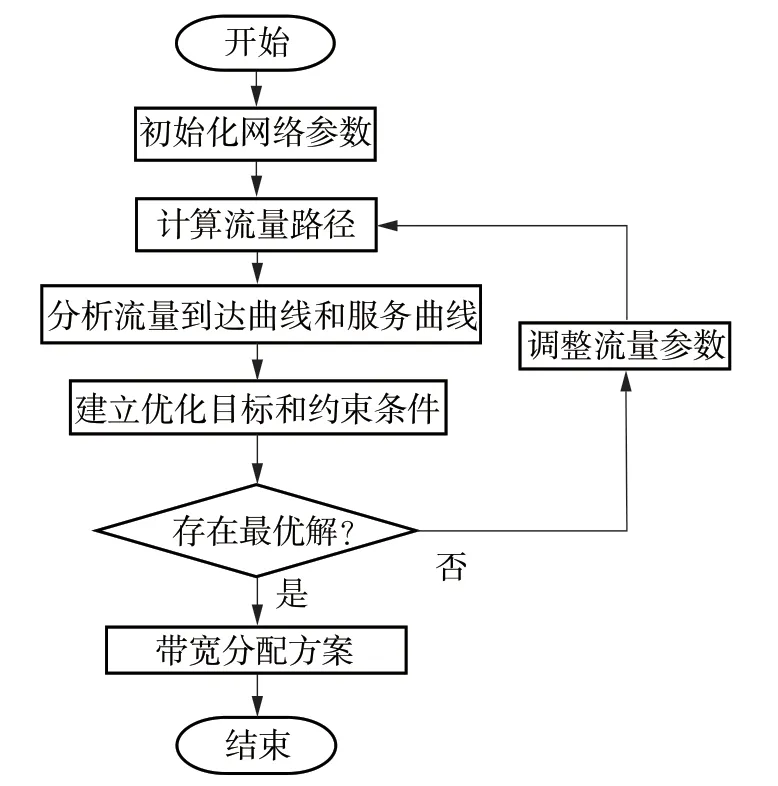
图5 文中带宽分配方法的流程图Fig.5 Flowchart of the proposed bandwidth allocation method

（1）建立网络模型，根据网络流量信息和拓扑结构，基于链路负载均衡的路由（LBR）算法为每条流量计算最优路径；

（2）基于网络演算和流量路径分析交换机出端口流量的最坏转发时延；

（3）设定目标函数，在满足带宽资源和时延限制的条件下，以作为求解参数，采用优化算法求解网络带宽分配方案；

（4）判断最终结果，如果存在最优解，则直接输出带宽分配结果，否则调整流量参数，返回步骤（1）再次执行优化流程。

2.2 基于链路负载均衡的带宽分配方法

2.2.1 基于链路负载均衡的路由算法

为了获得网络中交换机节点的最优带宽分配，需要对网络进行建模。首先将网络抽象成一个无向图，用G(V，E)表示，其中V为网络节点集合，主要包括Talker（T）节点、Listener（L）节点及Bridge（B）节点，E为网络边的集合，l(i，j)为节点Vi到节点Vj之间的链路，将网络中AVB 流量的数据集合用F表示，则对于流量f∈F，可用六元组表示为

式中，fst为流量类型（包括AVB_A和AVB_B两种类型），fp为流量周期，fl为帧长，fs和ft分别为流量的源节点和目的节点，fd为流量的截止时间。

由于基于网络演算分析AVB流量的最坏时延时，已经为TT流量的传输预留足够的带宽，以保证TT流量的传输，因此文中LBR算法以平衡各链路AVB流量的负载为目标，为AVB流量计算最优路径。

首先，分别计算A、B 两类流量中每条流量的链路负载率，表示为

然后，将两个类别的流量分别按照Ufi从大到小进行排列，根据各类别流量的排列顺序依次为A、B两个类别的每一条流量fi计算最优路径。具体的最优流量路径计算步骤如下：首先，计算fi的前k条最短路径，生成路径集R，依次计算每条路径下非终端直连链路的负载率，文中将其表示为该路径下包括的所有相同传输方向链路的当前链路负载率的最大值，对于fi的第j条路径ri，j∈R，该路径中的第k条链路lj，k的负载率Ul(lj，k)表示为

路径ri，j的最大链路负载率表示为

取所有路径中最大链路负载率最小的路径作为fi的最优路径，如果存在多个最小值的路径，则以最短路径优先，所以fi的最优路径可表示为

2.2.2 AVB数据流的最坏时延分析

为了评估网络中AVB 流量的最坏时延，通常采用网络演算进行建模分析，网络演算的主要工具是到达曲线和服务曲线，其中到达曲线描述了数据流随时间t到达网络节点的数据量（单位bit），通常采用漏桶模型表示为

式中，ρ为数据流的平均达到速率，b为数据流的最大突发报文长度。

服务曲线描述了数据流随时间t离开网络节点的数据量，通常延迟服务曲线表示为

式中，v为数据流的服务速率，θ为服务开始前数据流延迟的时间。

如图6所示，到达曲线和服务曲线的最大水平偏差h（α，β）即为该数据流的最坏转发时延，由于TSN采用混流传输，所以AVB流量的最坏时延会受到其他流量传输的影响。

图6 到达曲线和服务曲线示意图Fig.6 Schematic diagram of arrival curve and service curve

由于AVB 流量的传输受TT 流量传输的影响，因此要分析AVB 流量的服务曲线，需要先分析TT流量的到达曲线。Zhao 等［14］给出了（0，t］内TT 流量的到达曲线，Li 等［16］为了减小计算复杂度，将TT流量的时间窗口视为一个漏桶模型，因TAS 根据GCL 门控列表周期性地控制TT 流量的传输，故在每个宏周期内，TT 窗口的长度保持不变，即在TT窗口的最大突发是有限的，TT 流量的到达曲线表示为

式中，bTT和ρTT分别为TT流量的最大突发量、平均到达速率。在最坏情况下，bTT=ρTT∑wTT，ρTT=CwpwTTAS，∑wTT为所有TT 窗口长度之和，wpw=∑(wTT+wGB)为所有保护带窗口长度wGB和TT 窗口长度wTT之和。

基于TT 流量的到达曲线可以进一步得到交换机出端口的AVB流量的服务曲线，即

式中：w=，是在TT 流量影响下AVB流量的带宽系数；θX为AVB_X的最坏初始时延，A类和B类流量的最坏初始时延分别为［16］

当链路传输速率为C时，周期性传输的数据流量f的到达曲线可以表示为［18］

式中，ρf=8flfp为流量f的平均到达速率，bf=8fl(1-ρfC)为f的最大突发量。考虑f从节点k经过最大转发时延Dk后到达节点k+1，故f所经过的两个相邻节点的到达曲线的约束为［19］

为了计算流量f在交换机出端口的最大转发时延，需要先获得同一类别的聚合流量在该端口的到达曲线［20］，即

由于AVB 流量通过CBS 进行转发，所以端口流量的到达速率会受到上一个节点出端口的CBS机制的影响，使得该端口的最大突发流量受到限制。Li等［16］引入整形器曲线，描述了在CBS机制下流量的到达曲线，即

综合式（15）和式（16），交换机端口流量的到达曲线可表示为αg(t)和曲线的最小下界，即

如前文所述，网络节点的最坏时延可表示为流量到达曲线和节点服务曲线之间的最大水平距离，故流量f在节点k的最大转发时延表示为

流量f的端到端最坏时延表示为传输路径上所经过的节点（包括源节点和交换机节点）最坏时延之和，即

2.2.3 带宽分配计算

在规划好流量的最优路径后，就可以基于网络演算得出每个交换机节点的最坏转发时延，由上述分析可知，节点的最坏时延是节点带宽的数学表达式，故通过建立目标函数，并以为未知参数，采用启发式算法可以求解最优带宽值。

考虑到网络带宽资源有限，需要建立带宽分配的约束条件，首先应该满足CBS中信用值非溢出条件［14］，即

其次是满足端口带宽约束。端口带宽约束主要是为了保障TSN 中BE 流量的基本传输，通常给BE流量预留25%的带宽，剩下的75%带宽分配给AVB流量，故AVB流量的总带宽满足

然后是满足节点处理能力约束。在网络演算理论中，每个节点的流量到达速率应该小于该节点提供的服务速率，并且由于TT 窗口时隙期间AVB 流量的信用值会被冻结，考虑到TT时隙窗口的影响，节点到达速率和服务速率的约束表示为

式中，fX为经过该节点的流量。

最后是满足时延约束。流量的端到端最坏时延应该小于流量的截止时间，故时延约束表示为

为了求解网络的带宽分配方案，文中以最小化网络节点的最坏延迟总和为目标函数，即

基于上述目标函数和约束条件就可以采用启发式算法求解出每个节点出端口的逻辑带宽文中改进之处在于：首先，在带宽分配流程中添加了基于链路负载均衡的路由计算步骤，从而增加带宽求解成功率，提升流量的可调度性；其次，优化了各端口的参数配置，将负载均衡链路所连接的交换机出端口的带宽设置为相同值，减少了启发式算法中决策变量的数量，提升了带宽求解速度且求解的带宽值更优。

3 实验与评估

为对文中提出的带宽分配方法进行验证，文中设计了3 组实验：①实验1 对比分析了LBR 算法与最短路径优先（SPF）算法对AVB 流量可调度性的影响，以验证路由算法的重要性及LBR 算法的有效性；②考虑到文中带宽分配问题是优化约束问题，当采用启发式算法求解时，不同的求解算法会有不同的表现，因此实验2选择粒子群优化算法（PSO）［21］和遗传算法（GA）［22］对比分析了LBR-SP 算法的求解速度和求解质量，以选择出更适合文中带宽分配问题的求解算法；③实验3 在同一种启发式算法下，将LBR-SP算法与带宽分配MP算法［12］进行对比，以验证文中提出的带宽分配方法的改进效果。

实验1 的拓扑结构如图7 所示，包括5 个交换机节点B1-B5、20 个终端（T1，T2，…，T10；L1，L2，…，L10）。实验基本参数包括：全双工物理链路C=100 Mb/s；流量数量为10～100；fp=1.0，1.5，2.0 ms；fl在500～1 000 B 范围内；源节点从T 节点中随机选择，目标节点从L节点中随机选择。文中采用网络演算进行网络性能评估，当流量f的路径使得该路径下每条链路的负载率小于最大可分配带宽的75%时，可认为该流量满足带宽求解的基本约束，进而进行调度求解。文中将AVB 流量的可调度性定义为

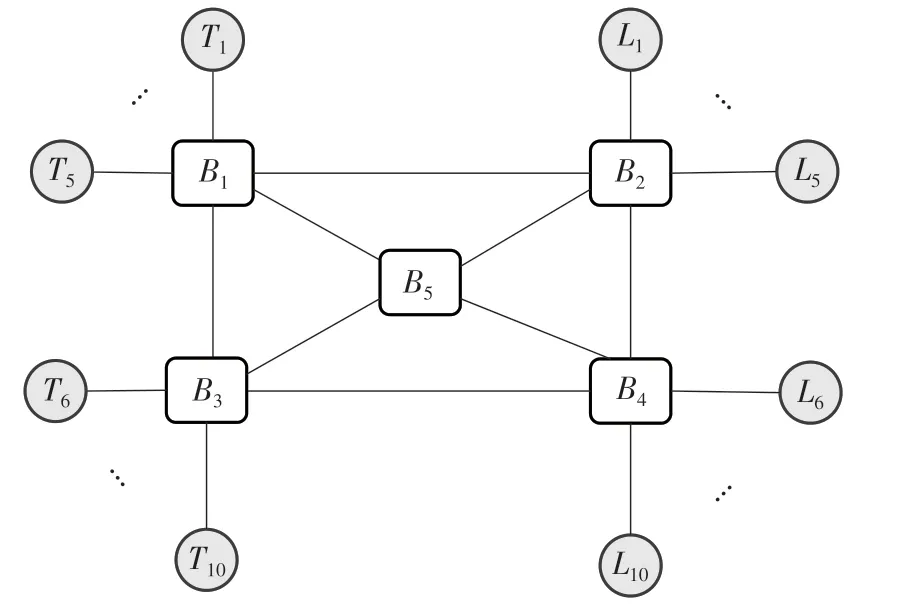
图7 网络拓扑结构Fig.7 Network topology structure

式中，Ns为满足带宽求解基本约束的流量的数量，NAVB为总的AVB流量的数量。

两种算法的AVB 流量可调度性对比如图8所示。从图中可以发现，在流量总数较小时，LBR算法和SPF算法均能满足带宽求解的基本约束，随着流量数量的增加，LBR算法相比于SPF算法的可调度性提升了15～45个百分点。因为SPF算法总是选择最短路径进行传输，随着流量数量的增加，很容易使某个节点的流量超过该节点的处理能力，而LBR算法通过均衡链路负载，会使得流量的分布相对均衡，在流量数量较小时，每个节点的流量不会超过该节点的处理能力，提高了流量的整体可调度性。

图8 两种算法的AVB流量可调度性对比Fig.8 Comparison of AVB traffic schedulability between two algorithms

实验2 的基本参数包括wGB=80 µs，wTT=120 µs，fA.p=1 ms，fB.p=2 ms，fd=10 ms，BE 流最大数据帧长=1 000 B，TTAS=1 000 µs。实验拓扑结构以图7 中的T5作为源节点，L6作为目的节点，共有3条传输路径，每条路径传输的流量数量为20，包括10 条A 类流量和10 条B 类流量，表1 共设置了5组包含不同帧长的实验数据。PSO和GA算法参数设置如下：种群规模和迭代次数均为100，PSO 算法的惯性权重、个体记忆和集体记忆分别为0.8、0.5 和0.5，GA 算法的变异概率和交叉概率分别为0.2 和0.8。两种算法的求解质量和求解速度对比如表2 所示，图9 为两种算法求解第1 组实验数据时的收敛性对比。

表1 不同路径下A/B类流量的帧长设置Table 1 Frame length settings of class A/B traffic under different paths

表2 PSO和GA算法所求解的目标函数最优值和求解时间Table 2 Optimal value and solution time of the objective function solved by PSO and GA algorithms

图9 PSO和GA算法的收敛性对比Fig.9 Comparison of convergence between PSO and GA algorithms

从表2可以看出，在相同的种群规模和迭代次数下，针对文中的LBR-SP 求解问题，PSO 算法相对于GA 算法能够获得更优的解。由于迭代次数相同，PSO算法的求解时间与GA算法无明显差异，但略微较短。因为PSO算法通过迭代更新每个粒子在空间的位置和速度来搜索最优解，由于粒子之间信息共享，所以算法的运算效率高，且有更多的机会得到全局最优解。由图9 可以看出，PSO 算法可以更加快速地收敛于更优的解，更加适用于文中基于网络演算的带宽分配问题的求解。

实验3 对比分析了LBR-SP 与MP 算法的性能，并且还考虑了当链路负载不均衡（non-LBR）时，带宽参数的设置对带宽分配的影响，实验参数设置同实验2，且以实验2 中更优的PSO 算法作为求解算法，实验结果如图10所示。

从图10（a）可以看出，基于LBR 算法获得的带宽分配结果可以使网络的端到端时延始终小于non-LBR 算法，因为网络负载均衡时，通过启发式算法更易求出各端口的最优解。当网络负载不均衡时，每个端口的流量分布差异较大，求解的带宽值往往不是所有节点的最优带宽值，会使部分节点的最大转发时延较大，最终导致流量的端到端时延之和较大。当路由算法一致时，SP 的求解质量相较于MP 更优，因为MP 会为每个端口计算出一组带宽值，SP 将所有均衡链路的端口都设置为统一的参数，当采用PSO 算法求解时，适当减少求解参数，会更容易得到全局最优解。

从图10（b）可以看出，SP 的求解速度相较于MP 提升了1 倍以上，这是因为采用PSO 算法求解时，参数越少，求解速度越快。随着网络中交换机节点数的增多，MP 的求解参数也会增加，从而导致求解时间增加，而SP 的求解参数并不会随着交换机节点数的增加而显著增加，当网络规模较大时，求解速度会相对更快。综合图10可以看出，LBR-SP 能够提升带宽求解速度，并且可以获得使流量的最坏时延总和更小的带宽分配结果，在大规模动态变化的TSN中有更好的表现。

4 结语

针对TSN中基于CBS的流量带宽分配问题，文中提出了一种基于链路负载均衡的AVB流量带宽分配方法。相比于现有相关研究，在最坏转发时延分析方面，文中采用了包含有整形器曲线的AVB流量最坏时延分析模型，使得目标函数更加严谨；在带宽分配问题的构建流程方面，文中考虑了路由对AVB流量可调度性的影响，在带宽分配流程中添加了基于链路负载均衡的路由计算步骤，从而增加带宽求解的成功率，提升流量的可调度性；在带宽分配问题的求解方面，针对现有带宽分配方法在网络复杂时无法快速求解带宽的问题，文中通过减少带宽参数来提升求解速度。然而，仅减少参数虽然能提升求解速度，但会影响带宽分配的效果，因为各端口的负载存在差异，设置相同的带宽参数是不恰当的，而结合链路负载均衡路由，将均衡链路所连接的端口设置为同一参数，在提升求解速度的同时也可以获得更优的带宽分配结果。实验结果表明，相比于现有的基于网络演算的带宽分配方法，文中LBR-SP 方法可以使AVB 流量的可调度性提升15～45个百分点，带宽求解速度提升1倍以上，且得到更优的带宽分配结果，为大规模动态变化的TSN带宽分配场景提供了一定的参考。未来的研究工作主要包括流量的路由优化以及时延敏感流的可靠性研究等。