G2连续的单位四元数样条曲线

王 倩, 刘美含, 周 彤, 周奕含, 徐宇飞

(辽宁师范大学 数学学院,辽宁 大连 116081)

随着计算机动画和机器人控制技术的飞速发展,刚体运动曲线的设计变得愈发重要[1].通常情况下,人们使用位置曲线和朝向曲线来共同生成刚体运动曲线.对比于传统的欧拉角法和旋转矩阵表示法,单位四元数更适合表示刚体的朝向,其优势是可以避免万向节锁死现象的发生.因此,单位四元数曲线近年来被广泛应用于刚体运动曲线的设计中.但是并非所有的曲线都能够被推广到单位四元数空间S3中,本文围绕如何构造单位四元数曲线问题进行研究.

1985年,Shoemake[6]利用球面线性插值(slerp)方法构造了具有C1连续性的单位四元数Bézier曲线,成功将四元数应用到了刚体运动中.1995年,Kim[7-8]给出了定义在旋转群SO(3)或S3上的单位四元数曲线的一般代数构造方法和高阶导数微分公式,其做法是将欧氏空间中样条曲线的基函数由累加形式转化为累积形式,从而得到相应的四元数曲线,该类曲线保留了在3中的一些几何和微分性质.以Kim和文献[3-5]为基础,邢燕等[9]对单位四元数插值样条曲线的连续性与插值性问题进行了研究,构造了基于四次多项式的C2连续单位四元数插值样条曲线.Tan等[10]给出了基于参数五次多项式的单位四元数插值样条曲线的构造方法,该曲线能够达到G2连续,并且可以通过改变参数调整曲线形状.孙楠等[11]研究了Bézier四元数样条曲线的性质和端点处的高阶导矢,构造出具有C2连续性的四元数插值样条曲线.文献[12]将Gamma样条推广到四元数空间,研究了四元数样条曲线的连续性问题和局部控制参数对曲线形状的影响.

受以上研究的启发,结合四元数理论,本文构造了基于四次多项式的含参单位四元数样条曲线,并对其在每段连接点处的连续性进行了研究.该曲线不但能够精确地插值任意给定的四元数序列,而且可以通过改变参数来整体调整样条曲线的形状,满足了平滑性和计算效率的要求.

1 预备知识

1.1 四元数的运算

类似复数的定义,四元数的一般形式为

i2=j2=k2=ijk=-1,

ij=-ji=k, jk=-kj=i, ki=-ik=j.

为了方便,四元数q还可以表示成另一种形式:

四元数的加减法定义为

四元数的乘法定义为

q=(cosθ,sinθ(a,b,c)),

给定一个向量v=θ(a,b,c)∈3,其中,θ∈[0,π],(a,b,c)∈S2,指数映射可以解释为从向量v到单位四元数的映射:

q=exp(v)=(cosθ,sinθ(a,b,c))∈S3.

当限制|θ|<π时,映射exp是一一映射,则可以定义它的逆映射对数映射:

v=log(q)∈3.

所以单位四元数q对于实值指数α的幂可以定义为qα=exp(αlog(q)).

1.2 四元数曲线

给定2个单位四元数q1和q2,则q1到q2之间的最短距离可以用测地线方程来表示[7]:

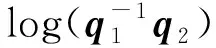
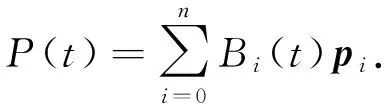
给定控制顶点q0,q1,…,qn∈S3.根据Kim的构造方法[8],可以定义相应的四元数曲线如下:

(1)

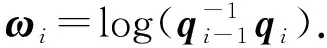
式(1)可改写成简单四元数曲线乘积的形式:

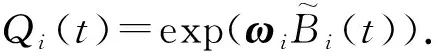
(2)

2 C2连续的单位四元数样条曲线

欧氏空间中样条曲线的构造方法有很多,本节内容引用了韩旭里等[3]的构造方法,得到的四次样条曲线可以直接插值给定的点列,并且能够达到C2连续.

给定点列p1,p2,…,pn∈和参数λ∈,令p0=p1,pn+1=pn.对于每4个相邻的点pi-1,pi,pi+1,pi+2(i=1,2,…,n-1),构造四次多项式曲线[3]:

Pi(t)≜Pi(t,λ)=(B0,4(t),B1,4(t),B2,4(t),B3,4(t),B4,4(t))

(3)

将Bernstein基函数做线性组合,则可以得到四次多项式曲线的另一种表达方式:

(4)

其中,

(5)

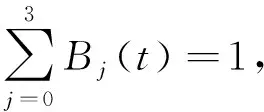
对于i=1,2,…,n-1,t∈[1,n],令

P(t)=Pi(t-i),i≤t≤i+1.

(6)

显然P(t)是由n-1段Pi(t)依次拼接而成的四次多项式样条曲线.

2.1 基于四次多项式的单位四元数样条曲线的构造

基于Kim等人[8]的工作,本节在S3空间中构造基于四次多项式的单位四元数样条曲线.

定义1给定四元数q1,q2,…,qn∈S3,数列u1,u2,…,un∈和参数λ∈,令对于i=1,2,…,n-1,在每个子区间[ui,ui+1]上定义单位四元数曲线:

(7)

对于i=1,2,…,n-1,u∈[u1,un],令

Q(u)=Qi(u),ui≤u≤ui+1,

(8)

则Q(u)是一条单位四元数样条曲线.显然Q(u)是由n-1段Qi(u)依次拼接而成的.

当u∈[ui,ui+1]时,有

2.2 基于四次多项式的单位四元数样条曲线的连续性

单位四元数样条曲线Q(u)保持了欧氏空间中样条曲线P(t)的许多重要性质.由于所构造的样条曲线Q(u)是由n-1段Qi(u)拼接而成的,因此研究相邻两段单位四元数曲线在连接点处的光滑性即可.

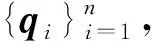
证式(7)可以改写为

(9)

将ui,ui+1代入式(9),得

Qi(ui)=qi,Qi(ui+1)=qi+1.

对Qi(u)关于u求一阶导,得

(10)

由式(2)知

将ui,ui+1代入式(10),得

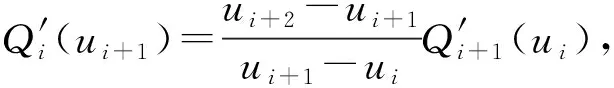
对Qi(u)关于u求二阶导,得

(11)

由式(2)知

将ui,ui+1代入式(11),得

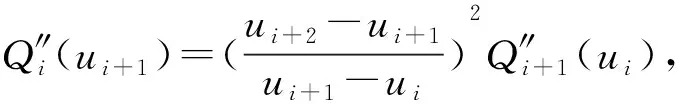
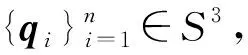
3 实验算例

通过将各类单位四元数样条曲线应用于刚体运动,以对比实验的形式来说明本文提出的构造方法的可行性和有效性.

随机选取一组四元数作为插值点

构造由3段四元数曲线组成的单位四元数样条曲线,应用于刚体运动中.图1中刚体运动均是由不同单位四元数样条曲线作朝向曲线生成的,位置曲线均选取为直线.为了更好地观察刚体的旋转情况,将插值点设置成了易于区分的颜色.

图1(a)和图1(b)展示了本文构造的单位四元数样条曲线作朝向曲线生成的刚体运动图像.图1(c)是邢燕等人[9]的单位四元数样条曲线作朝向曲线生成的刚体运动图像.特别地,此方法是本文所得方法在λ取0.5时得到的结果.图1(d)是Tan等人[10]的单位四元数样条曲线作朝向曲线生成的刚体运动图像.可以看出,令λ=0.5时,应用本文方法得到的刚体运动图像接近檀结庆方法的刚体运动图像,但是本文方法构造出的单位四元数样条曲线次数较低.

为了进一步探讨参数的选取对本文构造方法的影响,将单位四元数样条曲线应用于刚体运动,绘制刚体中心的旋转运动轨迹.随机选取另一组四元数作为插值点

图2(a)～图2(i) 展示了λ取不同值时刚体中心的旋转运动轨迹.可以看出,λ的取值越接近0.5时,轨迹曲线在插值点处就越顺滑.λ的取值接近0时,轨迹曲线在刚经过插值点后变得尖锐,对应时刻的刚体旋转速度加快,其余时刻轨迹曲线较为平坦.λ的取值接近1时,轨迹曲线在即将到达下一个插值点时变得尖锐,其余时刻较为平坦.如果λ取值为负或者>1时,插值点附近的轨迹曲线就会扭结(如图2(a)(i)),所以一般在[0,1]中选择参数值.

4 结 论

本文提出一种基于四次多项式的G2连续单位四元数样条曲线的构造方法.该曲线能够精确地插值任意给定的四元数序列,并且可以通过改变参数大小来调整整体形状.此方案能够应用于计算机动画和机器人控制中的刚体运动曲线设计.在后续的研究中,将会考虑如何添加多个参数使得曲线能进行局部调控,以及改良调配基函数,使曲线具有更高阶的几何连续性.