空化器锥角对超空泡射弹阻力与弹道影响数值研究
邹多艺佳,朱 墨,蔡希文,郭则庆
(1.南京理工大学 机械工程学院, 南京 210094;2.南京理工大学 瞬态物理国家重点实验室, 南京 210094)
0 引言
超空泡射弹是一种利用超空泡原理研制、由火炮发射攻击水下目标的高速弹药,可用于执行拦截鱼雷、摧毁水雷、反蛙人等多种任务。水下高速运动时超空泡射弹在由其头部空化器产生的超空泡中高速行驶,可获得90%以上的减阻效果[1]。通过合理的流体动力外形设计维持弹道稳定,使其在水下无动力、无控制飞行较远距离后仍有足够的动能摧毁目标。超空泡射弹在发射或入水时可能受到微小扰动,使弹丸在运动过程中尾部周期性碰撞空泡壁面,这种现象称为尾拍运动[2]。尾拍运动是超空泡射弹维持运动稳定性的重要方式,因此受到国内外研究人员的广泛关注。
Savchenko[3]首先从理论上提出了超空泡航行体在水下维持稳定的4种方式和各自的速度范围;Rand等[4]研究了超空泡射弹尾部与空泡壁面周期性碰撞的尾拍规律;Ruzzene等[5]基于哈密顿原理得到了超空泡射弹尾拍的柔性多体动力学方程;赵成功等[6]分析了初始扰动和质心位置对超空泡射弹尾拍运动的影响;陈伟善等[7]比较了平头弹、凹口弹、锥头弹的尾拍运动特性及水动力的影响因素。黄宝珠[8]分析了不同材料密度对射弹尾拍运动特性的影响。祝许皓[9]分析了不同初始偏航角以及不同初始滚转角速度下,俯仰运动对射弹尾拍运动的影响。
空化器是超空泡射弹中诱导生成超空泡的特殊部件,空化器形状对空泡形态、减阻特性和运动稳定性都有重要影响。常见的空化器包括圆盘形空化器和锥形空化器,因圆盘形空化器结沾湿面和体积有限,难以安装自导装置。锥形空化器有相对更大的沾湿面和体积,对自导装置的安装更加有利同时减阻效果更好。因此锥形空化器对于超空泡射弹在某些方面有更好的性能。Savchenko[3]在大量实验基础上,通过外推法推出了锥形空化器空化数趋近于0时的阻力系数;贾力平等[10]对空化器线形与超空泡形态的关系及其阻力特性进行了数值仿真研究。李强[11]分析了2种空化器形状的超空泡射弹在空化和全沾湿2种情况下减阻特性和空化数变化。Mansour[12]研究了不同空化器形状对超空泡流动特性的影响。林明东等[13]优化设计了锥形空化器,研究了空化数等因素对超空泡航行器空化器设计的影响规律。黄小腾[14]研究了超空泡航行体的不同锥角空化器的流体动力特性以及空泡形态。栗夫园等[15-16]通过水洞实验分析了锥形空化器的流体动力特性,并在此基础上对各种锥角的空化器的流体动力特性进行了仿真分析。Pendar等[17]研究了不同湍流模型和空化模型对球形和圆锥形空化器性能的影响。李懿霖等[18]分析了空化器直径对超空泡航行器受力性能和空泡性能的影响。王瑞等[19]通过分析不同外形的空化器,得到了头型空化器参数对超空化流场特性的影响规律。魏平[20]分析了4种头锥形状超空泡射弹的流体动力学特性和空化特性。
尽管国内外许多研究人员对空化器进行了大量研究,但是目前对锥形空化器的研究成果集中于锥形空化器的减阻效果和对空泡形态的影响,然而空化器锥角对超空泡射弹的尾拍运动规律和弹道特性的研究却鲜见报道。因此本文中利用数值仿真方法研究了在保证空化器产生的空泡在射弹尾部尺寸相同的条件下,空化器锥角对射弹的尾拍运动规律和弹道特性的影响,研究结果可为超空泡射弹的头部外形设计提供参考和依据。
1 数值模拟方法
1.1 流体控制方程
超空泡射弹水下运动过程涉及气液两相流动问题,本文中选取VOF多相流模型进行描述。由于在射弹速度小于900 m/s时,液体的可压缩性对阻力特性和空泡形态影响较小[1,21],本文中研究工况射弹速度为600 m/s,故采用不可压缩流体模型,空泡内部为饱和蒸气压3.54 kPa。
混合介质的连续性方程为

(1)
式(1)中:ρm为混合流体密度,ρm=ρvαv+ρl(1-αv),ρv、ρl分别表示水蒸气和液态水的密度,αv、αl分别表示水蒸汽和液态水的体积分数,ui(i=1,2,3)为平面笛卡尔坐标系下的速度分量,xi(i=1,2,3)为对应方向上的坐标,t为时间。
动量守恒方程为

(2)
式(2)中:P为流体压力,μm=μvαv+μl(1-αv)为混合介质的动力粘性系数,μv、μl分别为水蒸气和水的动力粘性系数,μt为湍流动力粘性系数。
1.2 空化模型
两相之间质量传输方程可采用Schnerr-Sauer空化模型,该模型计算效率高,数值稳定性强。相变率的表达式如下
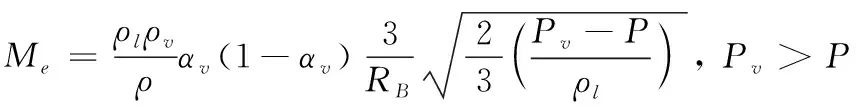
(3)

(4)

(5)
式(3)—式(5)中:Me、Mc分别为蒸发率和冷凝率;αv、ρv分别为蒸汽相体积分数和密度;Pv为饱和蒸汽压;RB为气泡半径;n为单位体积空泡数。
1.3 湍流模型
k-ε湍流模型在被Launder and Spalding提出以来[22],已经成为计算工程流动最常用的湍流模型。它以其鲁棒性、经济性和对大尺度湍流流动的合理精度而广受欢迎,并被证明可以有效地模拟超空泡射弹空化过程产生的湍流流动[23]。Realizablek-ε湍流模型在k-ε湍流模型基础上提高了对高雷诺数的预测精度以及剪切流动描述准确性。
湍动能k方程为

(6)
湍流耗散率ε方程为

(7)
式(7)中:k为湍动能,ε为湍流耗散率,Gk、Gb分别为速度梯度和浮力引起的湍动能,E为时均应变率,Sk、Sε为源相,C1=max[0.43,η/(η+5)],其中η=Ek/ε,C1ε=1.44,C2=1.9,σk=1.0,σε=1.2。
1.4 模型及网格划分
本文中主要研究锥形空化器射弹的不同锥角对射弹运动特性的影响。所采用的6种射弹模型除空化器锥角和直径差异外,其他参数均相同,模型及主要尺寸参数分别如图1和表1所示。
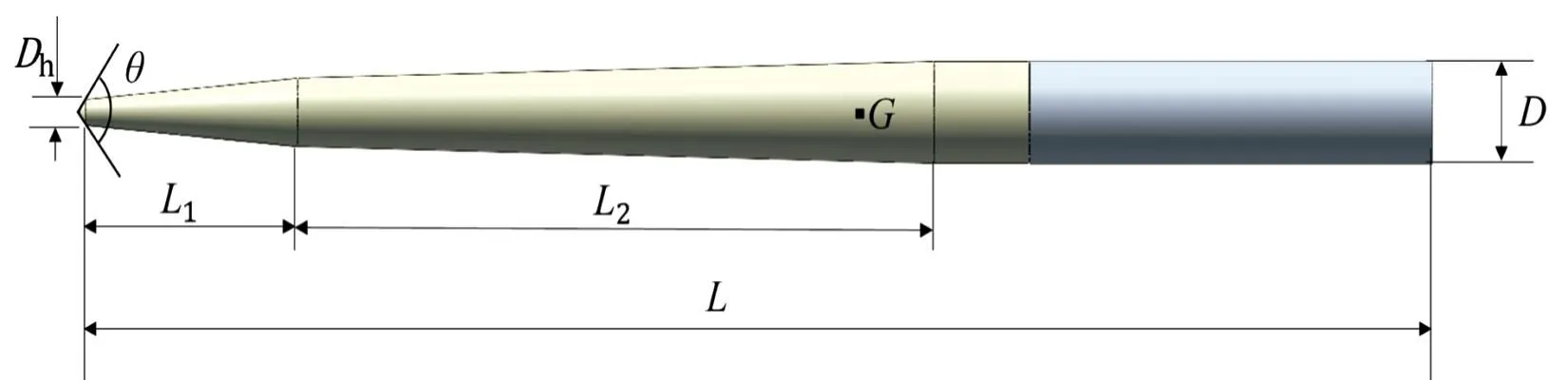
图1 射弹模型

表1 射弹主要参数
为避免“边界效应”对射弹附近流场产生影响,计算域选取φ20L×30L(L为弹长)的圆柱形流域,入口边界距弹头10L,X轴位于弹体轴线上,如图2所示,边界条件选择速度进口和压力出口。射弹位于4 m水深下,以600 m/s初速运动。
采用移动计算域模型,以射弹建立体坐标系,计算域网格整体跟随射弹一起运动,通过6自由度求解器解算射弹的平动速度和绕质心转动角速度。由于文中给定的初始运动状态相对于XOY平面对称,且由于流场的对称性,射弹在运动过程中绕X轴和Y轴转动量很小,可以忽略不计,为简化分析,射弹限制在XOY平面内平动,且只能绕Z轴转动。
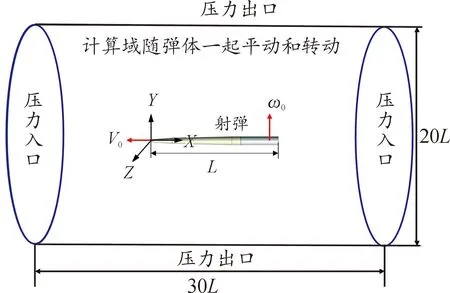
图2 计算域及边界条件示意图
整体计算域均采用六面体结构化网格,为实现空泡形态和弹丸受力的精准捕捉,在根据经验公式计算的空泡轮廓和弹体表面附近加密网格,空泡轮廓处的网格径向尺寸不超过1.5 mm。在不改变总体网格分布规律的前提下,改变对应线节点的数量建立网格数量分别为155万、300万、500万3种不同数量的网格,在速度为600 m/s、零攻角的工况下进行模拟,所得空泡对比如图3所示。可以看出,在300万网格和500万网格下计算的空泡形态基本一致,空泡直径的最大相对偏差低于0.2%,而在155万网格下计算的空泡略大,最大相对偏差达1.2%。综合考虑计算精度和效率,文中选取数量为300万的网格进行计算,弹体附近的网格如图4所示。
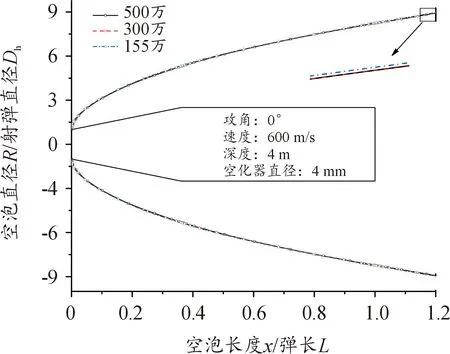
图3 不同网格密度的计算结果

图4 弹体附近网格
为验证文中建立的数值计算模型,采用Hrubes实验[24]中的弹型及工况在此计算模型下进行仿真,将仿真所得空泡尺寸与Hrubes实验结果、经验公式[25]进行对比如图5、图6所示。图中可以看出此模型下仿真的空泡与Hrubes实验照片中空泡轮廓基本一致,实验数据与仿真曲线也基本吻合,相对偏差低于2.1%,空泡轮廓尺寸更贴近于试验结果。将射弹形成稳定完整空泡时的阻力系数与文献[26]的实验结果对比,结果如图7所示,计算得到的射弹阻力系数与实验相对偏差低于4.8%。综上说明文中所述数值模型在模拟高速射弹空化流场时具有较高的精度。

图5 仿真空泡与试验空泡对比

图6 仿真数据与试验数据对比
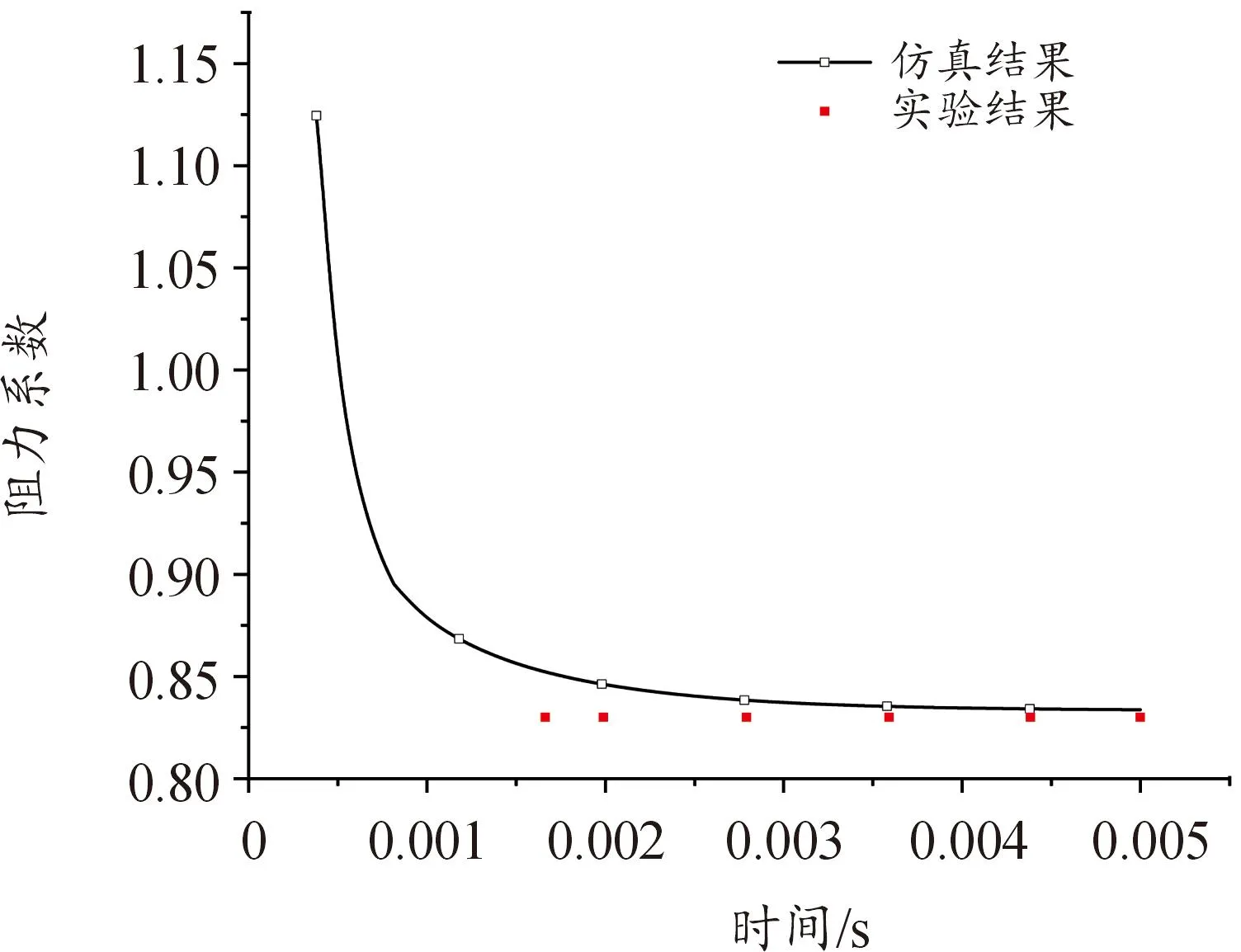
图7 仿真与实验阻力系数对比
2 结果与讨论
2.1 模型设计
现有锥形空化器锥角对减阻效果及运动特性影响的研究中,都是在空化器直径相同的条件下,通过改变空化器锥角进行比较研究。在实际应用中超空泡射弹能够对水下目标形成有效毁伤的速度大约为100 m/s,以实际毁伤效果为基础设计超空泡射弹时,需要保证射弹在100 m/s时仍能保持稳定的空泡形态且完全包裹射弹,此时随着锥角的改变,超空泡射弹空化器直径也需要改变。如图8所示为120°空化器锥角超空泡射弹空泡轮廓图,在弹尾处空泡刚好包裹射弹。根据弹尾处空泡尺寸,分别设计了60°、80°、100°、120°、140°、160° 6种空化器锥角的超空泡射弹,此时空化器直径及弹尾处空泡尺寸见表2,其中与120°弹尾空泡尺寸对比最大尺寸偏差为0.71%。可以看出,为了使在相同速度下的空泡尺寸相同,锥角越小的空化器的直径越大。
下文计算所采用的射弹均采用这6种空化器头型,即空化器锥角和直径均不相同,但末弹道时尾部空泡尺寸相同。

图8 100 m/s速度下超空泡射弹空泡轮廓(120°锥角)

表2 不同锥角空化器直径及弹尾空泡尺寸
2.2 阻力特性比较
首先仅赋予射弹X方向移动的自由度,将6种不同空化器锥角的射弹,在零攻角、速度600 m/s条件下计算空化器所受阻力Fdc。如图9所示为空化器锥角与射弹阻力Fdc关系图,随着锥角增大Fdc先增大后减小,在140°左右最大。
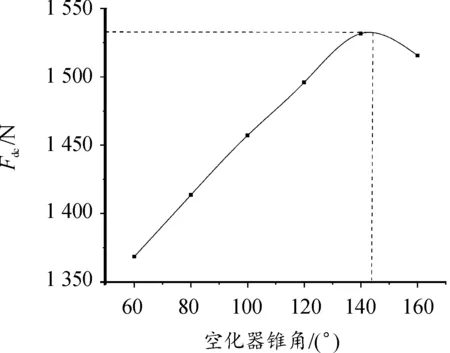
图9 空化器锥角与空化器阻力Fdc关系图
射弹在稳定运动时,空化器所受阻力为:

(8)
式(8)中:S为空化器表面面积;p为空化器表面压力;θ为空化器锥角。沿空化器表面径向压力值分布如图10所示,随着空化器锥角的增大,作用在空化器表面的压力峰值也在不断增大,但当锥角超过120°后,空化器表面压力峰值基本不变。不同空化器锥角的减阻效果的不同,主要由锥角变化和空化器直径变化两部分导致。当空化器锥角为60°~140°时,锥角增大导致阻力增大的部分大于空化器直径增大导致阻力增大的部分,因此射弹所受阻力随着锥角的增大而增大;当空化器锥角为140°~160°时,锥角增大导致阻力增大的部分小于最大空化器直径增大导致阻力增大的部分,因此射弹所受阻力随着锥角的增大而减小。综上所述,随着空化器锥角的增大射弹所受阻力先增大后减小,在140°左右所受阻力最大。
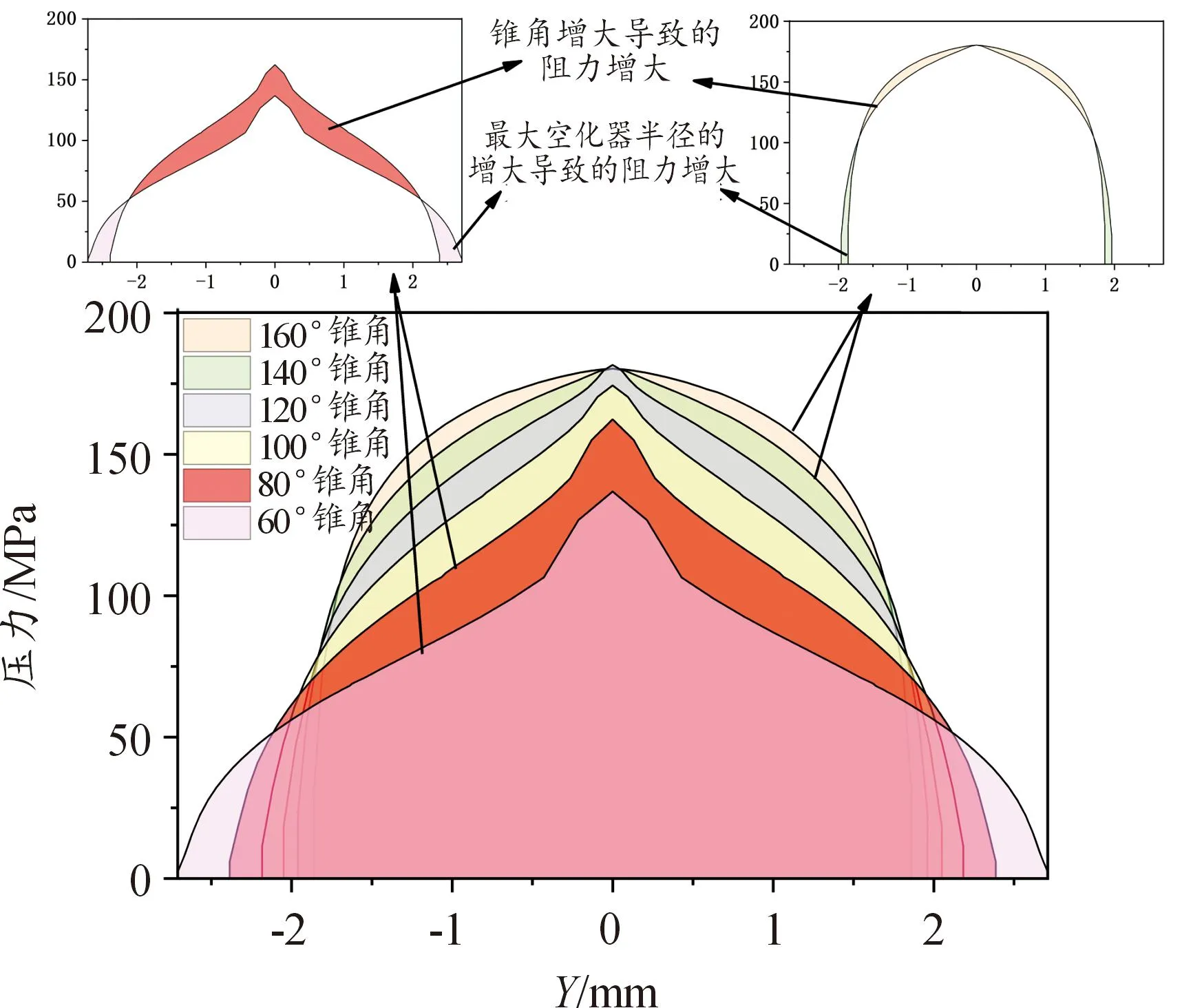
图10 空化器径向压力分布
2.3 尾拍特性比较
射弹在尾拍运动过程中,随着俯仰角增加,弹体的沾湿状态可分为3个阶段:① 头部沾湿阶段,除弹头空化器以外弹身全部包裹在空泡内;② 弹尾沾湿阶段,射弹尾部刺入空泡壁,沾湿面积随俯仰角增大而增大;③ 肩部沾湿阶段,射弹肩部沾湿,同时在沾湿部分形成二次空泡并包裹后部弹体,降低弹尾沾湿面积。
为简化分析,将射弹尾拍运动限制在XOY平面内。6种不同空化器锥角射弹先固定射弹俯仰角为0、运动速度固定为600 m/s条件下运动至形成稳定空泡。然后在再设置绕Z轴转动初始角速度ω0=10 rad/s,利用UDF和6DOF方程计算器在XOY平面内自由运动,直至射弹速度降至100 m/s结束计算。图11为其俯仰角变化曲线,可以看出空化器锥角为60°~100°的射弹俯仰角在大于零的范围呈现周期性波动,以“单侧尾拍”的运动形式保持稳定。空化器锥角为120°~160°的射弹俯仰角在中轴线上下呈现周期性对称波动,以“双侧尾拍”的运动形式保持稳定。

图11 俯仰角对比
图12分别为锥角为60°和120°的射弹在单个尾拍周期内的运动和受力示意图。射弹初始处于头部沾湿阶段,由于初始角速度的作用俯仰角增大,此时在空化器产生倾覆力矩Mh,其大小随着俯仰角的增大逐渐增大。随着俯仰角的增大,射弹尾部刺入空泡壁,进入尾部沾湿阶段(图12第3行),此时由尾部产生反向力矩Mt抵消部分Mh,减缓射弹俯仰角增长。随着俯仰角继续增大,射弹肩部刺入空泡壁,进入肩部沾湿阶段,由于肩部的沾湿中心位于质心之后,此时肩部也产生反向力矩Ms继续抑制射弹俯仰角的增长(图12第4行)。当Ms和Mt的合成力矩大于Mh时,射弹的尾拍角速度逐渐下降,降为零后开始反向运动向下尾拍,再次进入头部沾湿阶段。当射弹还未跨过空泡中轴线,射弹头部持续产生颠覆力矩(图12第5行)。由于空化器所受力矩与其锥角大小有关,如图13所示,锥角越小头部产生力矩越大,当锥角范围在60°~100°时,头部产生过大力矩致使射弹不能越过空泡轴线,再次向上尾拍进行“单侧尾拍”运动。当锥角范围在120°~160°时,头部产生力矩较小,射弹越过空泡轴线向下尾拍形成对称的“双侧尾拍”运动。
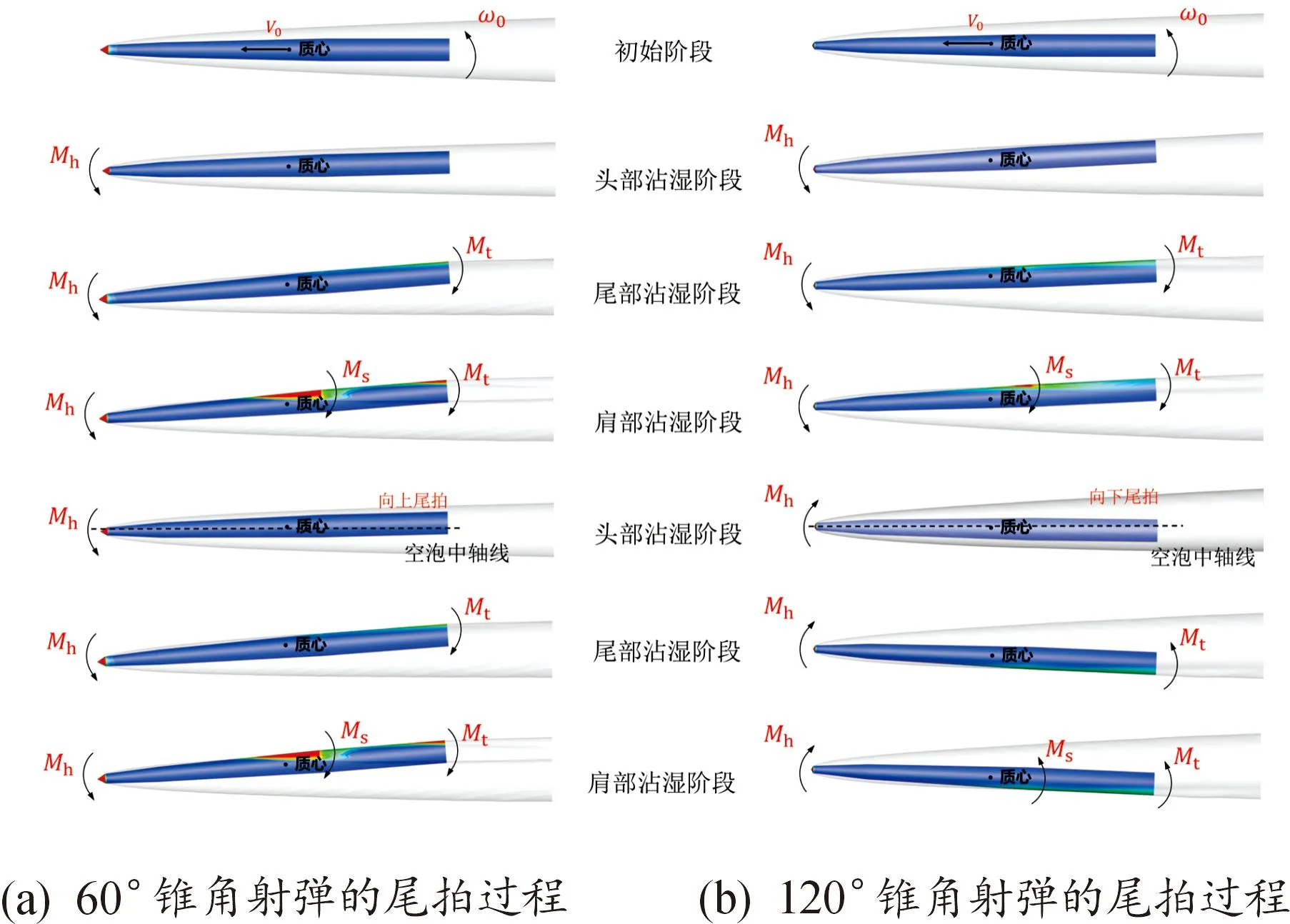
图12 锥头弹的2种尾拍运动方式

图13 不同空化器锥角头部力矩对比
图14为6种不同射弹尾拍角速度随时间变化的比较,可以看出,由于空化器产生力矩Mh不同,第一次尾拍时间和角速度峰值也不同,锥角越小第一次尾拍时间越早,且角速度峰值越大。空化器锥角范围在60°~100°射弹的角速度变化趋势大致相同,均表现出“N”型变化趋势。
其原因主要是“单侧尾拍”过程中,射弹由肩部沾湿阶段进入至头部沾湿阶段,射弹还未越过空泡轴线时,由于头部产生较大的力矩作用于射弹且与角速度方向相反,射弹角速度迅速减小并改变方向,故角速度呈现出“N”型变化趋势。且空化器锥角为60°时,由于头部力矩过大,一次尾拍过程中呈现多次拍打的特性;空化器锥角范围在120°~160°射弹的角速度变化趋势大致相同,均表现出“凹”型变化趋势。其主要原因“双侧尾拍”过程中,射弹由肩部沾湿阶段进入至头部沾湿阶段,射弹还未越过空泡轴线时,由于头部产生的力矩较小,射弹角速度逐渐减小但改变角速度方向。当射弹越过空泡轴线时,头部产生的力矩与角速度相同,角速度又逐渐增大,故角速度呈现出“凹”型的变化趋势。且“凹”型越大,每次尾拍周期越长。
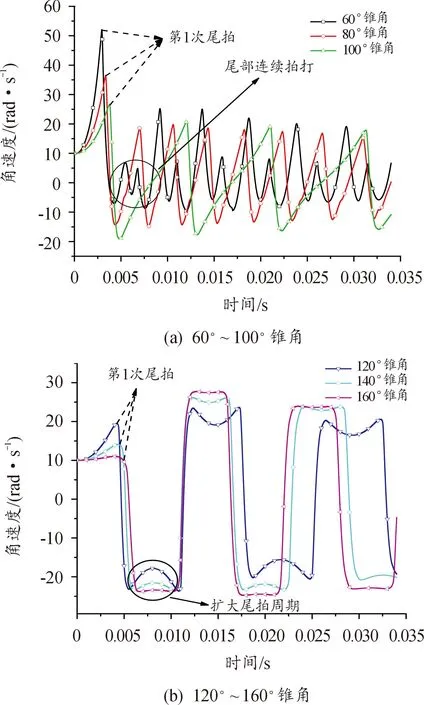
图14 不同空化器锥角角速度比较
2.4 弹道特性比较
定义射弹的阻力系数为

(9)
式(9)中:Cd为弹体阻力系数;Fd表示射弹的阻力;ρ0为水的密度,取998.2 kg/m3;S为射弹最大截面面积。
如图15所示为不同空化器锥角射弹阻力系数随时间的变化曲线对比。可以看出,在尾拍过程中空化器的阻力系数曲线均呈现出周期性振荡变化,每一次尾拍阻力系数都间歇性增大。在60°~100°范围内,虽然空化器的阻力随着锥角增加而增大,但由于空化器越小其沾湿时间越长,导致总体平均阻力反而越大,如图15(a)。在120°~160°范围内,3种射弹的尾拍过程和周期都相似,空化器阻力对其总体阻力占主导作用,因此该3种射弹中120°锥角射弹平均阻力最小。
定义射弹速度降为100 m/s时的射弹X方向行程为其有效射程。如图16所示,6种射弹的最大和最小有效射程分别为90 m和83.2 m。射程由大到小顺序为:100°、80°、120°、60°、160°、140°。其主要原因为:空化器锥角越小的射弹的空化器阻力系数越小,故在头部沾湿阶段小锥角空化器有更好的减阻效果。但不同空化器锥角射弹的尾拍形式不同,在肩部沾湿阶段和尾部沾湿阶段,空化器锥角范围在60°~100°,随着空化器锥角的增大射弹的尾拍阻力系数越小。空化器锥角范围在120°~160°,随着空化器锥角的增大射弹的尾拍阻力系数先增大后减小。故X位移的大小关系呈现如上特性。

图15 阻力系数对比

图16 X方向位移随速度的变化
射弹Y方向位移代表了其弹道偏移量,即射击精度。图17为射弹Y方向位移随速度的变化,在有效射程下Y方向的最大和最小位移分别为-13.7 m和0.06 m,由大到校的顺序为:60°、80°、100°、160°、140°、120°。120°~160°锥角的射弹Y方向相差不大,最大为0.164 m;60°~100°锥角的射弹Y方向位移明显增大,且随着锥角的减小而增大。其主要原因为:60°~100°锥角的射弹以“单侧尾拍”形式运动,射弹俯仰角一直维持在正向范围,其持续受到向下的升力,射弹Y方向速度不断增大。120°~160°锥角的射弹以“双侧尾拍”形式运动,射弹俯仰角正负不断交替,其所受升力也在正负交替,在较长时间范围内相互抵消。故Y方向上小空化器锥角相较于大空化器锥角位移更大。

图17 Y方向位移随速度的变化
综合分析可以看出,在本文中所采用的射弹结构下,60°~100°锥角的空化器由于单侧尾拍运动导致方向偏移量较大,不具有实际使用价值。锥角在120°~160°范围时弹道偏移量较小,其中120°锥角综合减阻效果最好,有效射程最大。
3 结论
本文中以末端弹道空泡尺寸相同的前提对不同空化器锥角的超空泡射弹的阻力特性、尾拍运动特性及弹道特性进行了对比分析。所得主要结论如下:
1) 在末端弹道空泡尺寸相同的情况下,锥角越小相应的空化器直径越大,空化器阻力在锥角为140°时达到最大值,在该角度两侧呈单调减小趋势。
2) 射弹在尾拍运动过程中,在空化器锥角范围在60°~100°,射弹以“单侧尾拍”的运动形式保持稳定,角速度变化呈现“N”型变化趋势。空化器锥角范围在120°~160°,俯仰角在中轴线上下呈现周期性对称波动,以“双侧尾拍”的运动形式保持稳定,角速度变化呈现“凹”型变化趋势。
3)X方向位移不仅与空化器减阻效果有关,也与其尾拍特性有关。有效射程的大小顺序为:100°>80°>120°>60°>160°>140°。
4) 锥角较小射弹为单侧尾拍运动,其Y方向位移随着锥角减小而增大,对射击精度影响很大。锥角较大的射弹由于双侧尾拍受到往复对称的升力,在Y方向位移较小,且锥角为120°时最小。
本文中所得结论可为超空泡射弹的空化器设计提供重要的理论依据。

