基于螺线管式的舰船模拟磁源建模仿真研究
陆斌杰,张晓兵,戴忠华
(1.海军工程大学 兵器工程学院, 武汉 430033; 2. 92279部队, 山东 烟台 264003; 3.军事科学院国防科技创新研究院, 北京 100071)
0 引言
水下磁源技术广泛应用于磁探潜[1]、磁诱饵[2-3]、水雷战[4-5]等领域。文献[6]基于舰船磁场分析,采用二轴磁线圈能以较高精度模拟舰船磁场。文献[7]采用基于N层导电介质模型的电极模拟舰船磁场。螺线管式能较好地模拟舰船特定方向的通过特性[4]。国外基于螺线管式磁源的装备型号有瑞典SAAB公司的自航声磁扫雷具SAM3,荷兰的遥控感应扫雷系统(netherlands remote controlled influence minesweeping system,NLRCIMS),美国的先进轻量感应扫雷系统(advanced lightweight influence sweep system,ALISS),美国QinetiQ公司的浅水感应扫雷系统(shallow water influence minesweeping system,SWIMS),美国海军的基于高温超导磁体的闭环扫雷具MAGNUSS等。从国外发展现状能够看出,基于螺线管式磁源的研究一直处于热点。
螺线管式磁源的磁场特性是决定舰船磁场模拟性能的关键因素,要准确掌握螺线管式磁源的磁场分布,必须进行大量实测,但是实测数据的获取费时、费力,同时又难以掌握全部磁场数据[8]。因此,必须构建磁场数学模型。文献[4]采用单磁偶极子模型计算螺线管式磁源磁场,利用铁芯磁化曲线计算磁矩,该方法适用于远场情况,却没有考虑磁源的尺寸影响。
本文中基于磁偶极子阵列模型和旋转椭球体模型构建复合模型,通过仿真计算和船模对比仿真试验,结合空间磁场分布的定性分析和磁场时间序列相似度量2个维度,验证了螺线管式磁源的磁场模型的适用性,为磁探潜、磁诱饵、水雷战提供一定参考。
1 坐标系
磁场建模必须基于特定的坐标系,采用导航坐标系、载体坐标系、传感器坐标系,如图1所示[9]。
NED:导航坐标系或北东地坐标系,记为{n}=(xn,yn,zn),原点on固连于海平面某点,xn轴指向地理北方向,yn轴指向地理东方向,zn轴垂直地表向下。
BODY:载体坐标系,记为{b}=(xb,yb,zb),原点ob固连于载体中心,xb轴指向舰艏方向,yb轴指向右舷方向,zb轴垂直向下。
SENSOR:传感器坐标系,记为{s}=(xs,ys,zs),原点os固连于传感器中心,以传感器敏感轴为三轴,三轴符合右手定则。
载体6自由运动符号为:u、v、w分别为载体在载体坐标系中纵向速度、横向速度、垂向速度;p、q、r分别为载体在载体坐标系中的横摇角速度、纵摇角速度、偏航角速度;φ、θ、ψ分别为载体在导航坐标系中的横摇角、纵摇角、偏航角。
磁感应强度矢量从载体坐标系转换到导航坐标系的公式为
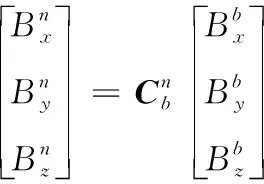
(1)
磁感应强度矢量从传感器坐标系转换到导航坐标系的公式为
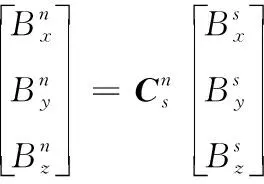
(3)

(4)
磁感应强度矢量从传感器坐标系转换到载体坐标系的公式为

(5)

图1 建模坐标系
2 磁场数学模型
根据螺线管式磁源的工作机理,磁场等效模型为磁偶极子阵列模型、混合模型。
2.1 磁偶极子阵列模型
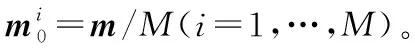
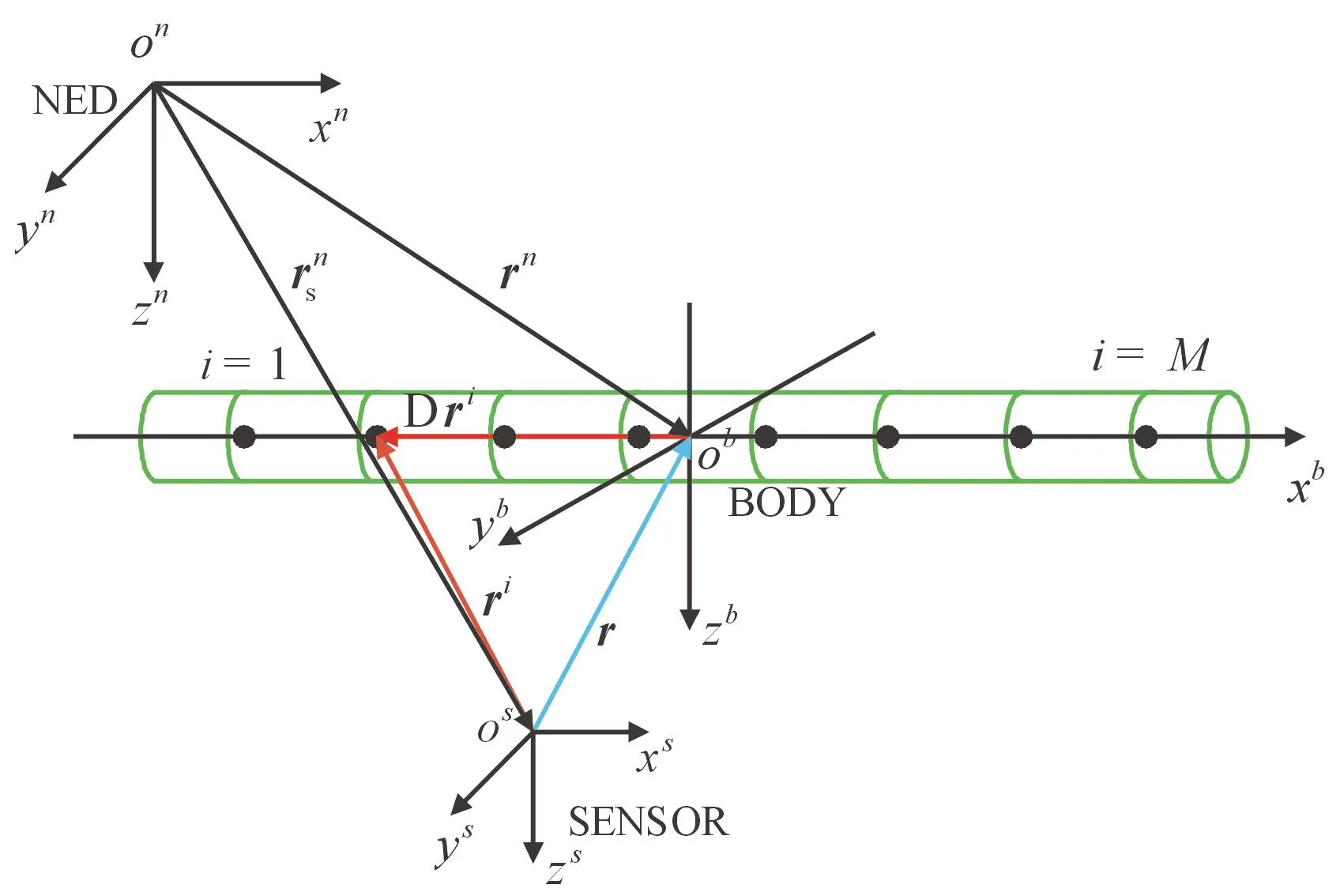
图2 磁偶极子阵列模型Fig.2 Magnetic dipoles array model
在s系中,螺线管式磁源磁感应强度为

(6)

(7)


(8)
式(8)中: Δψ=ψ-ψ′为目标航向与传感器x轴正向的夹角;Δψ与v的关系为

(9)

(10)
2.2 磁矩计算公式
由于线圈沿纵向排列,电流只产生纵向磁矩,因此采用单轴磁偶极子模型。
在b系中,空心螺线管总磁矩近似计算公式为[4]
m=IcNS
(11)
式(11)中:Ic为单匝线圈电流;N为线圈总匝数;S为线圈横截面积。
在b系中,带磁芯的螺线管总磁矩近似计算公式为[4]

(12)
式(12)中:t为线圈中心与螺线管中心的纵向距离;l为线圈宽度的一半;V为螺线管体积;ae为等效旋转椭球体长半轴,be为等效旋转椭球体短半轴,分别如下[10]:

(13)

(14)
2.3 混合模型
将螺线管式磁源磁场等效为均匀磁化旋转椭球体、磁偶极子阵列的混合模型,如图3所示,以磁体中心为原点建立b系;以传感器中心为原点建立s系。
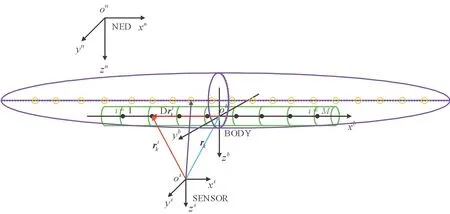
图3 混合模型Fig.3 Hybrid model


(15)

(16)

(17)
式(17)中:i=1,…,N对应磁偶极子模型,i=N+1对应椭球体模型。
综上,磁总场F为磁场矢量的模
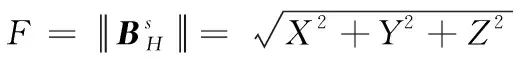
(18)
式(18)中:X、Y、Z分别为在s系中的三轴磁场。
3 磁场模型仿真及验证
设置不同的仿真条件,分别控制不同的变量进行仿真。然后将螺线管磁体仿真结果与船模试验结果对比,验证螺线管式磁源对舰船磁场的模拟程度。
3.1 仿真条件设置
仿真采用传感器坐标系下的磁感应强度矢量表示。影响螺线管磁体在传感器处的磁场的因素为传感器与磁体的相对位置、磁传感器敏感轴姿态、磁体的姿态、螺线管电流、螺线管线圈数、螺线管线圈方位、螺线管线圈间隔、复合模型中混合模型的设置等。
考虑传感器姿态在NED坐标系中仅受到偏航角的影响,忽略横摇角、纵摇角的影响;考虑磁体姿态在NED坐标系中仅仅受到偏航角的影响,忽略横摇角、纵摇角的影响。控制磁体的偏航角、螺线管线圈数、螺线管线圈方位、螺线管线圈间隔、复合模型中混合模型的设置为常量,分别控制传感器偏航角、传感器深度、磁体航速、传感器与磁体的横距、螺线管电流等4个变量进行仿真,仿真变量设置如表1所示。仿真常量设置如表2所示[10]。
3.2 通过特性仿真
针对情况1—情况5,磁体磁场时域曲线如图4所示。

表1 仿真变量设置Table 1 Simulation variations setting
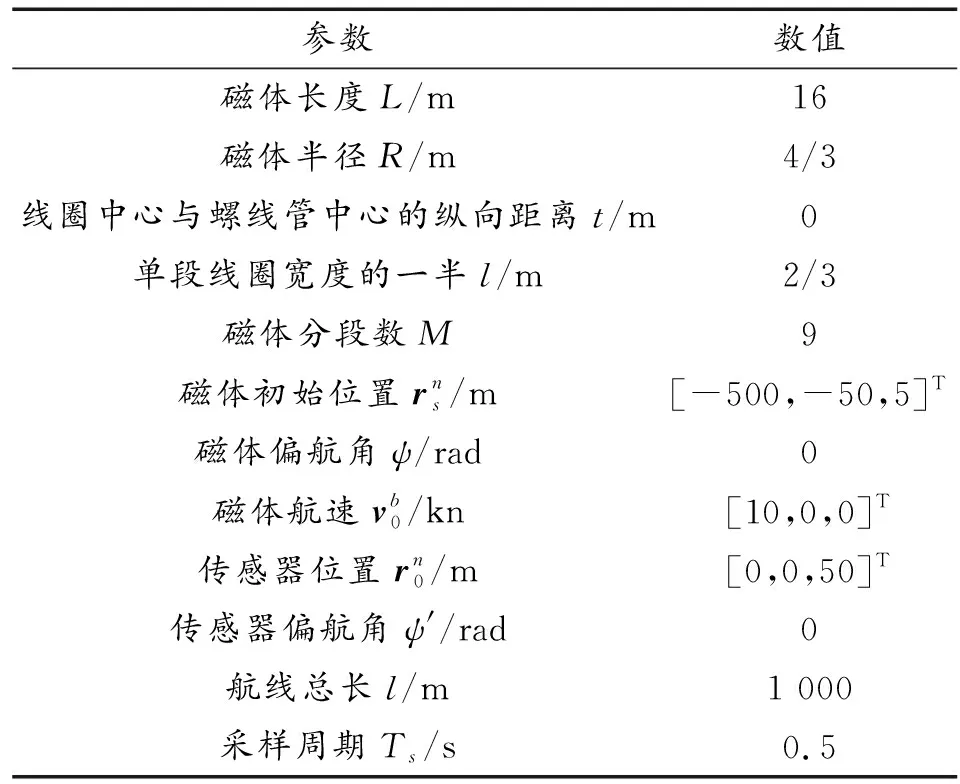
表2 仿真常量设置Table 2 Simulation constants setting

图4 螺线管式磁源磁场通过特性Fig.4 Magnetic field passing characteristics of solenoid magnetic source
由图4(a)、图4(b)可知,改变传感器的偏航角,只改变Bx、By,不影响Bz;由于偏航角改变90°,所以Bx、By互换。由图4(b)、图4(c)可知,减小传感器的深度,Bx、By的显著增大,Bz不增反降,这是由于螺线管仅存在mx。由图4(c)、图4(d)可知,改变磁体航速,不改变磁场强度,只改变磁场时域跨度。由图4(c)、图4(e)可知,改变电流幅值,改变磁场强度。由图4(e)、图4(f)可知,改变磁体与传感器的横距,改变磁场三分量的强度。 磁体磁场空间分布如图5所示。由图5(a)知,Bx关于xb轴对称分布,关于yb轴对称分布,磁场分布范围较大,在纵向和横向上从10 nT减小到1 nT范围延伸达500 m。由图5(b)知,By关于xb轴反对称分布,关于yb轴反对称分布,磁场分布范围较大,在对角方向从10 nT减小到1 nT范围延伸达700 m。由图(c)知,Bz关于xb轴反对称分布,关于yb轴对称分布,磁场分布范围较小,在横向方向从10 nT减小到1 nT范围延伸达250 m。由图(d)知,磁总场达8 000 nT。
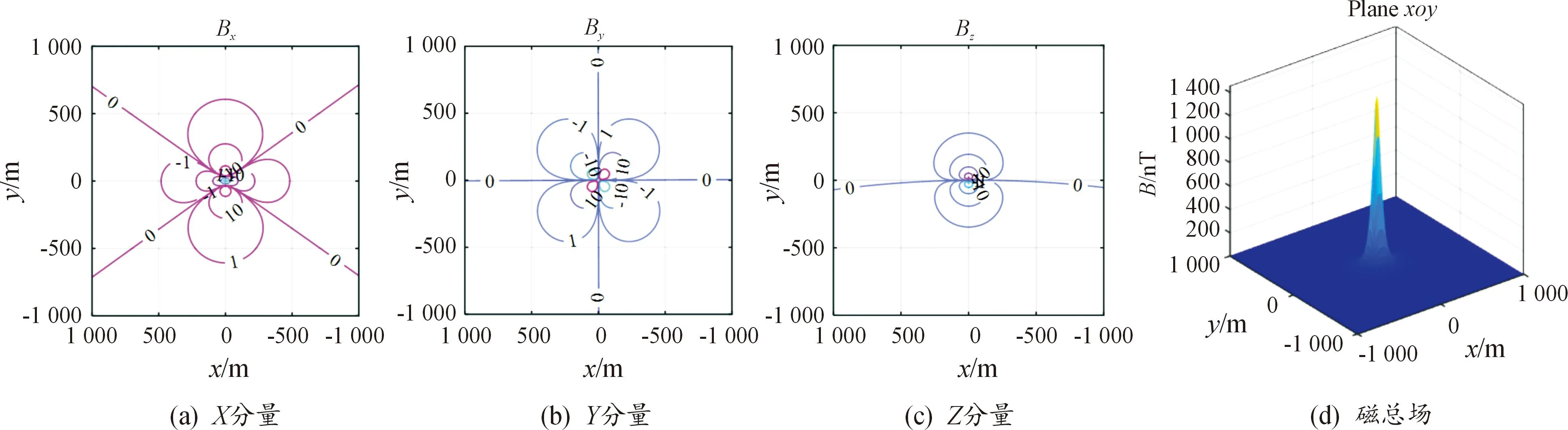
图5 磁体磁场空间分布(情况1)Fig.5 Spatial distribution of magnet magnetic field(case 1)
3.3 船模磁场对比
通过试验测量船模磁场,然后通过舰船磁场混合模型反演建立船模的磁场模型,利用船模磁场模型正演与磁体相同条件下的磁场,对比分析磁体和船模磁场特性。船模参数如表3所示。仿真条件设置与表1、表2相同。

表3 船模参数Table 3 Ship model parameters
船模磁场通过特性如图6所示。磁场时域特征对比如图7所示。船模磁场空间分布如图8所示。
下面分别针对5种情况进行对比分析。
1) 情况1
对比图4(a)和图6(a)可知,磁体三分量的变化趋势和相对关系与船模基本一致。但是磁体的Bx与Bx、Bz差异过大,船模的三分量幅值差异不明显。由图7(b)可知,磁体Bx磁倾角余弦与船模Bx磁倾角余弦相似性高,磁场标量梯度相似性较低。
对比图5和图8可知,磁体磁场Bx、By的空间分布与船模磁场Bx、By的空间分布相似性高,磁体磁场Bz的空间分布与船模磁场Bz的空间分布相似性低。
2) 情况2
对比图4(b)和图6(b)可知,磁体三分量的变化趋势和相对关系与船模基本一致。但是磁体的By过高,船模的By与Bz变化趋势一致,幅值差异明显。由图7(a)可知,磁体Bx磁倾角余弦与船模Bx磁倾角余弦相似性高,磁场标量梯度相似性较低。
3) 情况3
对比图4(c)和图6(c)可知,磁体Bx的变化趋势与船模基本一致。但是磁体的Bz与船模的Bz差异明显。由图7(c)可知,磁体Bx磁倾角余弦与船模Bx磁倾角余弦相似性低,变化趋势一致;磁场标量梯度相似性较低。
4) 情况4
对比图4(d)和图6(d)可知,磁体Bx的变化趋势与船模基本一致。但是磁体的Bz与船模的Bz差异明显。由图7(d)可知,磁体Bx磁倾角余弦与船模Bx磁倾角余弦相似性低,变化趋势一致;磁场标量梯度相似性低。
5) 情况5
对比图4(f)和图6(f)可知,磁体Bx的变化趋势与船模基本一致。但是磁体的By、Bz与船模的By、Bz差异明显。由图7(e)可知,磁体Bx磁倾角余弦与船模Bx磁倾角余弦相似性低,变化趋势一致;磁场标量梯度相似性低。
通过上述对比分析,可以看出未经优化(通过优化算法调整电流、磁源航速、磁源偏航角等参数)的磁源磁场,通过特性曲线、磁倾角余弦、空间分布能够在一定程度上模拟舰船的磁场特征。

图6 船模磁场通过特性Fig.6 Magnetic field passing characteristics of ship model

图7 磁场时域特征对比Fig.7 Comparison of time domain characteristics of magnetic field
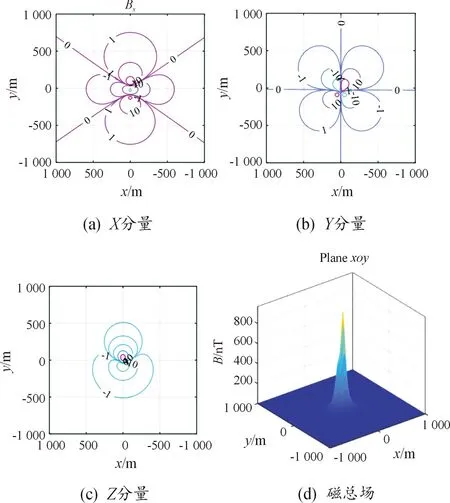
图8 船模磁场空间分布(情况1)Fig.8 Spatial distribution of model magnetic field (case 1)
3.4 基于欧几里得距离的相似性度量
为了度量磁场时间序列相似性,采用欧几里得距离(Euclidean distance,ED)对磁场时间序列进行相似性度量[11-12]。
ED适用于等长时间序列的相似性搜索,ED定义为[13]

(19)
式(19)中:fa=(a1,…,an);fb=(b1,…,bn)为2条等长的一元时间序列。
航速、航线总长、偏航角相同时,磁场相似度随电流变化规律如图9所示。

图9 磁场相似度随电流变化规律Fig.9 The variation of magnetic field similarity with current
由图9可知,单独控制电流变化,无法使得文中所选取的所有时域特征量的ED同时达到最小值,但是可以选取磁总场模值作为优化目标,当电流为6 500 A左右时,ED达到最小值。由表4可知,电流为10 000 A时的ED大于电流为6 500 A时ED,说明电流为6 500 A时的相似度高,结合图10可知,波形的直观对比也说明电流为6 500 A时的相似度较高。

表4 不同电流时的相似度Table 4 Similarity at different currents

图10 不同电流时的磁场时域特征量对比Fig.10 Comparison of magnetic field time domain characteristic quantities at different currents
4 结论
建立了基于混合模型的螺线管式磁源磁场模型,选取磁场通过特性、磁倾角余弦、磁场标量梯度等时域特征及磁场分布空域特征,通过仿真和船模试验验证了该模型对舰船磁场模拟的可行性。从磁场时间序列相似性的角度,通过基于欧几里得距离的相似性度量定量分析了螺线管对舰船磁场的模拟能力,同时也为区分螺线管式磁源与舰船磁场提供相应的参考,对工程实现螺线管式磁源模拟舰船磁场具有较大参考价值。

