电磁脉冲作用下NMOS管的电磁敏感性研究

李万银,张晨阳,查继鹏,郑国庆,李吾阳,张祥金

(南京理工大学 机械工程学院, 南京 210094)

0 引言

复杂的战场环境中充斥着各种干扰信号,其中电磁脉冲武器产生的高功率脉冲是最主要的电磁脉冲干扰信号,该脉冲耦合入电路中会使敏感器件发生失误甚至损伤[1]。NMOS管作为一种电压控制集成开关具有输入阻抗高、噪声低、成本低、工艺简单[2]等优点,常用在引信中控制信号的通断[3],但其电磁敏感性较差,若在战场电磁干扰如超宽带脉冲[4]或是电磁武器攻击下发生误通或者失效会直接影响导弹的正常工作[5]。

外部电磁脉冲(EMP)会以电磁波的形式向外扩散并通过耦合路径进入设备腔内,最终对器件造成损坏[6]。因此,人们对电磁脉冲对器件和电路的干扰和损伤现象越来越关注[7]。当耦合到NMOS管上的电磁能量过大时,可能会发生整流效应,导致NMOS管误操作甚至直接造成破坏[8]。针对电磁脉冲作用下NMOS管的损伤效应已有许多研究[9]。一项国外研究[10]指出,二次击穿属于热效应,其中PN结电流发生局部集中,从而导致PN结局部熔化。然而,该研究提出的理论模型过于简化,与实验结果的吻合并不好。D.C.Wunsch等[11]进行了70多种MOS管的阈值失效测试,并对实验数据进行了筛选和验证,最终建立了一个半经验公式。Egawa[12]建立并分析了PN结的失效模型,研究了雪崩击穿与二次击穿失效机理之间的联系,指出二次击穿的原因是由于雪崩击穿产生的负阻导致的,然而该理论的计算结果与实验存在较大差距,不够准确。国内的研究者任兴荣等[13]研究了二极管、晶体管在强电磁辐射下器件内的电流、电压密度和延迟时间等随输入脉冲变化的情况,得出了二极管、晶体管等在强电磁辐射下的损伤机理以及注入能量与注入干扰信号波形之间的关系。徐稳等[14]使用自编写的数学模型和程序计算出了微波条件下NMOS管内部的温度、电流和电压变化情况。范菊平等[15]对晶体管进行了微波注入,分析结果得出了器件在微波条件下的损伤位置和失效机理。

针对某型反坦克导弹在强电磁环境下失效的问题,发现起爆控制电路中NMOS管时常出现击穿、烧毁等现象,因此需要对NMOS管在电磁脉冲下损伤机理进行分析,研究其在战场环境下受到强电磁脉冲干扰下的电磁敏感性,即研究强电磁脉冲经过屏蔽外壳后耦合到晶体管上的干扰电压对其所造成的损伤效能。借助半导体仿真软件Silvaco TCAD建立相应的NMOS管模型,研究晶体管内部电流密度与电压密度随激励源注入的变化规律,对晶体管的损伤模式与损伤机理等特点进行分析。

1 NMOS管数值计算模型

仿真模拟外部电磁脉冲注入下的晶体管工作模式与损伤效应,需要计算半导体器件内温度分布,而器件热量受多种电学特性影响,由热传导方程、泊松方程、电子和空穴连续性方程组成如下热力学模型。热传导方程[16]为:

(1)

式(1)中:c为材料晶格热容,T是器件内部温度,κ为材料热导率,Pn为电子的绝对热导率,Pp为空穴的绝对热导率,φn和φp分别为电子和空穴的准费米势,q为基本电荷,R为符合率,kB为波尔茨曼常数。

电子和空穴连续性方程为:

(2)

(3)

式(2)—式(3)中:Jn和Jp分别指的是电子电流密度和空穴电流密度,n和p分别为电子密度与空穴密度。

其中,Jn和Jp的方程为:

Jn=-nqμn▽V+μnkBT▽n

(4)

Jp=-pqμp▽V+μpkBT▽n

(5)

式(4)—式(5)中:μn与μp为电子与空穴的迁移率。

泊松方程为:

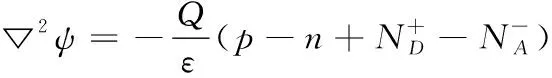
(6)

式(6)中,ε为电容率。

为了提高仿真的精度,精确模拟器件内各种电学特性对热能的影响,还需要考虑载流子的迁移、电场功耗与温度对载流子扩散输送的相互作用,其中对载流子的输送影响最为关键的是低场迁移率模型与载流子生成-复合模型。

仿真采用Klaassen提出的Philips统一迁移率模型来描述低场载流子迁移率。

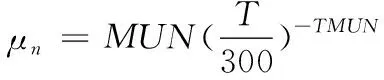
(7)

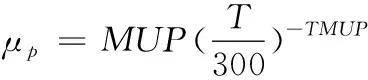
(8)

其中各模型参数值如表1所示。

载流子产生-复合过程考虑了SRH复合模型和俄歇复合模型。其中SRH复合即间接复合,SRH给出了电子重新组合的速率,该速率可表示为:

(9)

(10)

(11)

式(9)—式(11)中:Eupp为缺陷能级和本征费米能级之差,nie指的是本征载流子浓度(即未掺杂半导体中的载流子浓度)和本征空穴浓度,n1和p1分别指的是电子和空穴载流子浓度,τp和τn指的是和陷阱能级相关的参数。

俄歇复合模型为:

(12)

式(12)中:AUGN与AUGP分别为电子与空穴的俄歇复合因子,该模型参数见表1。

仿真意在模拟晶体管正常工作受到电磁脉冲时产生的损伤,所以边界条件使用欧姆接触,以金属材料铝作为电极,使晶体管与外部形成良好的欧姆接触,热量只能通过金属接触实现热量流通,器件的其余部分设置为绝热状态。

表1 模型参数

2 仿真流程与电路设计

使用Silvaco TCAD软件进行半导体器件仿真,对建模、材料、掺杂浓度与求解方式设置的基本仿真流程见图1。

图1 仿真流程图

仿真采用图2的电路模型,使用到外部脉冲电源VCC,外部稳定电压源V1,漏极电阻R1,源极与基极相连接地。

图2 仿真电路模型

3 器件结构建立

本仿真对晶体管做研究分析,建立NMOS管二维模型见图3,模型为典型NMOS管结构,为N-P-N结构,模型横向宽度为1 μm,衬底厚度0.6 μm,结深0.2 μm,图中基板(substract)与源极(source)接地,栅极(gate)外接电压源,漏极(drain)注入电磁脉冲信号,建模完成后以硅(Si)为衬底,进行离子注入与扩散,对衬底进行P型掺杂,掺杂浓度为2×1017/cm3,使用高斯分布,对源极与漏极进行N型掺杂,掺杂浓度为9.3×1019/cm3,源极与漏极间为P型半导体。实现管内浓度分布见图4。

图3 NMOS管二维结构图

图4 掺杂浓度分布图

NMOS管横向(沿x轴)杂质浓度分布见图5,NMOS管两端为高掺杂N区,中间0.4～0.6 μm处为低掺杂P区,由于电子与空穴间的相互吸引会导致高掺杂N区与低掺杂P区间形成一层耗尽层而隔断开路无法导通。

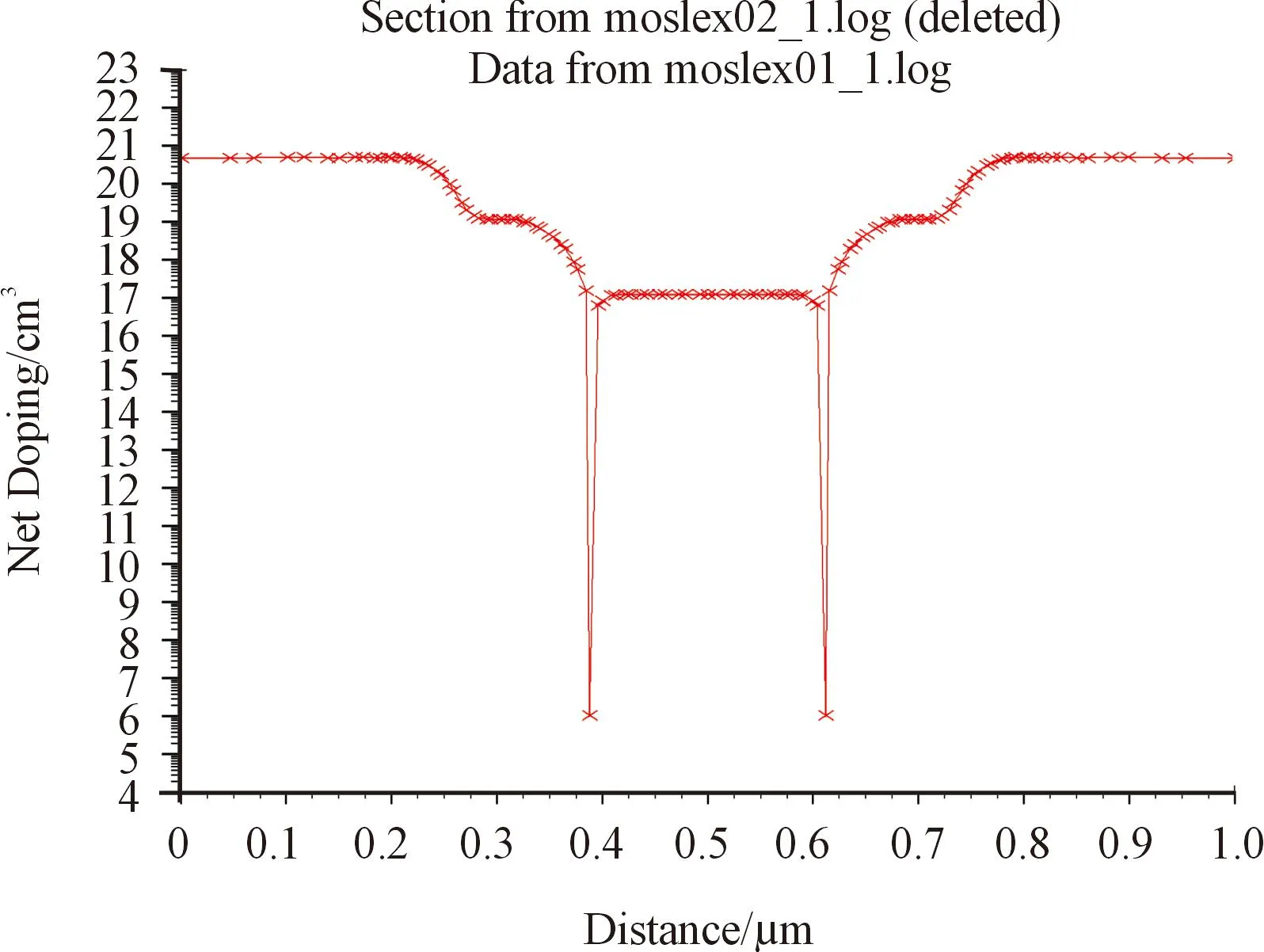
图5 纵轴掺杂浓度分布

4 仿真结果与数据分析

4.1 漏极脉冲电压注入仿真

对NMOS管的漏极、源极与基极均设定为理想欧姆接触,栅极与薄氧化层设置为薄绝缘栅条件并设置漏极为理想热接触。

根据仿真电路,保持源极与基极短接接地,栅极施加3 V电压使NMOS管处于正常工作区,此时从漏极上注入上升时间为1 μs,电压幅值为20 V的脉冲电压信号,脉冲与时间变化关系见图6所示。

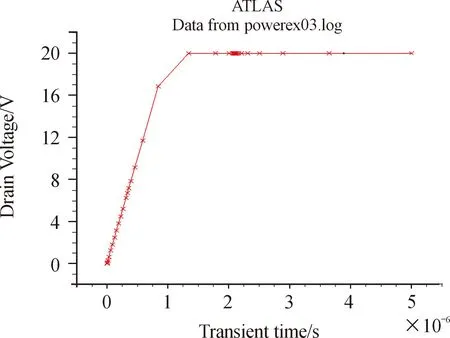
图6 20 V电磁脉冲与时间关系图

4.2 NMOS管的端特性随脉冲作用时间的变化规律

见图 7,NMOS管在正常工作状态下,由于栅极电压的施加使得空穴被排斥,向基极沉积,电子被吸引到栅极并在漏极与源极间形成一条窄N沟道区,连接起源极与漏极,使得电流能够流过,此时NMOS管导通,漏极电流迅速增大,但由于衬底中的电子数量有限,形成的沟道较窄,随着漏极电压的施加,漏极电流逐渐稳定,趋于不变,但在这过程中,漏极电压依然不断增加,最终超过雪崩击穿电压,造成NMOS管漏极击穿,在离散电子冲击下,发生雪崩倍增效应产生大量的载流子,因此漏极电流以指数级的趋势迅速增大,致使NMOS的局部导体温度升高,发生局部熔化,从而进一步增大电流,不断循环,最终造成NMOS管失效,甚至发生热击穿导致永久性失效。

图7 NMOS管端特性曲线

4.3 NMOS管的管内特性随脉冲幅值的变化规律

图8—图10分别为漏极注入不同幅值脉冲时的NMOS管内部的电场密度、电流密度与y=0.22 μm处的轴线上电场强度与电流密度分布图。

图8为NMOS管在脉冲幅值为10 V时的电压强度与电流密度参数示意图,此时NMOS管处于正常工作区,由于栅极施加3 V电压,在源极与漏极间搭起一条N沟道,连通起漏极与源极,形成高浓度电子区,在漏极电压作用下,电子随之迁移,形成电流,但并未出现雪崩击穿现象,而在y=0.22 μm 的横轴上,电压分布较为均匀,在漏极与衬底形成的PN结弯曲处由于PN结的结曲率效应,漏极PN结的边缘线上的电场强度出现峰值,稍大于平面区的电场强度,而衬底底部电场强度较小,电流主要集中在漏极与源极的直线上,与理论相一致,其他位置电流较小,在源极与漏极下方由于N型掺杂区与P型掺杂区形成耗尽区,电流密度趋于0。

图9为NMOS管在脉冲幅值为15 V时的电压强度与电流密度参数示意图,此时NMOS管的漏极与衬底处的电压峰值明显增大,而平面区的电场强度区域稳定保持在对数为5.1 V/cm上下,而电流密度与0.2 μs相比,虽然也增大了,同时漏极与源极下方的电流密度近0区域也减小了,但是电流密度相比并未发生明显变化,其他参数的分布情况也趋于一致,只是在数值上随漏极电压的增大而有所增加。

图8 t=1 μs幅值10 V NMOS管内部各参数分布情况

图9 t=1 μs幅值15 V NMOS管内部各参数分布情况

图10 t=1 μs幅值20 V NMOS管内部各参数分布情况

图10为NMOS管在脉冲幅值为20 V时的电压强度与电流密度参数示意图,由图10可见,此时沿着漏极与衬底处的PN结曲面上,电压强度只有少量增大,但电场分布区域大幅扩散,可以判断这是由于漏极施加大电压下,超过雪崩击穿电压,发生了雪崩击穿,电子发生碰撞、分离,产生大量离散电子,电子迁移穿过PN结流向衬底使得电场强度与电子浓度急剧增加,此时y=0.22 μm处的横轴线上电场强度与15 V 时相比只有峰值处电压有所增大,但横轴线上电流密度显著增大,验证雪崩效应确实发生,致使载流子数量大幅增加,并在2个PN位置处形成双峰值。查看管内温度分布与最大温度随时间变化见图 11,此时管内温度以漏极PN结处为中心,向外迅速减小,温度中心与电流密度峰值处、电场强度相重合,所以该区域的功率密度远大于其他部位,造成区域性的热量集中使得局部(PN结处)温度急剧升高,局部高温形成多处热斑,热斑处电流迅速增大,循环作用产生大量热能,使得温度0.83 μs时开始在短时间内从350 K升温至1 870 K,已经超过的半导体材料硅的熔点,这说明在短时间内NMOS管的漏极处已经发生高温熔融现象,产生了局部缺陷,对NMOS管的形成造成了永久性的损伤,这种现象属于热二次击穿。

根据1 μs内随着漏极电压注入的不断增大,器件内部电学特性与温度的变化规律,可以得出,一开始,在漏极电压未达到雪崩击穿电压前,NMOS管正常工作,电场分布均匀,电流密度在2个PN结处较为集中,温度保持在300～350 K以内,随着漏极电压超过雪崩击穿电压,漏极处的空间电荷区、电场强度分布扩大,在漏极PN结处发生电场强度峰值、电流密度峰值剧增现象,可以判断在PN结曲面上首先发生雪崩击穿,造成电学特性剧变,导致管内温度上升,电阻减小,电流增大,引起热二次击穿,使得温度迅速增大并超过硅的熔点,NMOS管发生永久性失效。

图11 幅值20 V NMOS管内部温度参数图

4.4 NMOS管击穿电压与栅极电压关系

图12为保持漏极电压注入幅值为20 V,扫描分析栅极电压分别为1、2、3、4 V时漏极电流与漏极电压变换关系曲线图,栅极电压影响着形成N沟道的宽度与源极、漏极连接时内阻的大小,随着栅极电压的增大,P掺杂区中越来越多的电子向N沟道汇聚,产生了更多的自由电子,相同漏极电压下未击穿时饱和区电流大小也随之越大,同时由上文可知NMOS管失效主要是因为漏极PN结反偏电压超过雪崩击穿电压导致,而栅极电压的增大减小了漏极PN结的反偏程度,从而增大了雪崩击穿电压,所以适当的增大栅极电压更有利于NMOS管的有效工作,但是需要注意,栅极电压的增大会导致栅极与漏极间的电压增大,而高电压会导致栅极氧化层击穿发生栅-源击穿,可以通过并联齐纳二极管进行优化。

图12 栅极电压1、2、3、4 V击穿参数图

4.5 仿真结果与实验验证

文献[17]进行了NMOS管漏极注入高功率微波实验,实验结果表明,从漏极注入微波时,主要发生的是漏极PN结击穿导致电流异常增大,热量累计,温度升高,致使电流进一步集中,循环之下出现热斑,局部温度迅速升高超过硅的熔点从而发生局部烧毁,这与图11所示的仿真结果相吻合。通过实验结果与仿真结果相验证表明,建立的二维电热模型能够很好的反映NMOS管内电场强度与电流密度随漏极注入脉冲幅值的变化规律,预测发生击穿时烧毁的位置。

5 结论

1) 通过使用Silvaco TCAD建立了NMOS管二维电热模型,仿真得到了漏极注入脉冲电压时NMOS管的管内瞬态特性,研究了管内电场强度与电流密度变化规律。

2) 通过图8—图10可得,漏极电压注入下,首先形成平稳N掺杂沟道,NMOS管正常工作,当漏极电压超过雪崩击穿电压18 V(见图7),发生雪崩击穿造成电流在结面处集中,发热增加造成结面处热量不断积累,持续作用下发生热二次击穿,管内电阻减小,局部电流与温度迅速上升并出现热斑,形成熔融通道,使得PN结烧毁,烧毁点主要发生在漏极PN结曲面处。

3) 栅极电压也会影响漏极雪崩击穿电压的大小,栅极电压越大雪崩击穿电压也越大,但栅极电压过大时栅-源易发生氧化层击穿。

4) 仿真数据与研究结果对于战场环境下半导体器件的电磁脉冲损伤机理和电磁敏感性研究具有参考意义。