基于灰度特征和众数原则的迭代双边中值滤波

衷 文，罗启强

基于灰度特征和众数原则的迭代双边中值滤波

衷 文，罗启强

（南昌工学院 信息与人工智能学院，江西 南昌 330108）

为了在去除红外图像的脉冲噪声的同时，有效保持和恢复图像的边缘细节，提出了基于灰度特征和众数原则的迭代双边中值滤波方法。此方法根据脉冲噪声的灰度特征以及众数原则，将取最小和最大值、而在邻域的灰度分布上孤立的像素识别为噪声。根据基于空间距离和灰度相似的加权系数，对邻域中的无噪像素与已经去噪恢复的像素进行频次加权，用频次加权中值作为噪声像素的估计值。其中，以迭代遍历的方式执行去噪处理，充分利用前次遍历处理的结果，以去除高密度噪声。实验数据证明，此方法去噪所得的PSNR和EPI值以及视觉效果均优于现有方法，具有更好的去噪性能。

脉冲噪声；红外图像；加权频次；双边中值滤波；边缘保持指数

0 引言

红外成像可以在夜晚和特殊环境下进行，但是往往亮度偏暗，且伴有脉冲噪声的干扰。脉冲噪声会降低红外图像的质量和视觉效果，对红外图像的分析和应用产生负面效果，噪声去除对红外成像非常重要。标准的中值滤波[1]对所有像素作统一去噪处理，会破坏无噪像素的原始信息。为了仅对噪声像素进行处理，Erkan等[2]提出一种开关中值滤波算法，将噪声像素检测出来，有针对性地进行去噪处理。Balasubramanian等[3]以重叠和迭代的方式调用标准中值滤波，虽然算法计算快速，但是对高密度噪声没有优势。Zhang等[4]基于证据推理提出多策略噪声检测方法和自适应中值滤波器，但是由估计的噪声密度决定去噪邻域的大小，缺乏局部鲁棒性。Erkan等[5]在自适应中值滤波的基础提出了频率中值滤波（adaptive frequency median filter, AFMF），用剔除噪声像素后的邻域像素的频率中值对噪声像素进行灰度估计，估计值更加接近像素的原始灰度。Shao等[6]对均值滤波进行改进，用自适应的加权均值滤波对噪声像素进行恢复，虽然算法计算快速，但是去噪效果的提升不明显。

为了更好地保持图像的细节特征，徐超等[7]提出了基于形态学级联运算的加权均值滤波，在对噪声进行抑制的同时，增强红外图像的轮廓特征。Liu等[8]用拉普拉斯金字塔对图像进行多尺度分解，用双边滤波对各尺度分解图像进行去噪处理。很显然，对多尺度分解图像的多重去噪处理会破坏像素之间的相关性，从而造成图像的模糊。为了实现多种决策的优势互补，以去除高密度噪声，Goel等[9]提出一种非对称自适应修剪的均值滤波算法（modified decision based unsymmetric adaptive neighborhood trimmed mean filter，DAMF），其中融合了非局部均值滤波、裁剪均值滤波和自适应中值滤波。顾雅青等[10]提出一种模糊滤波器，但是其仅根据最小和最大灰度值进行噪声检测，而红外图像中取最小值的无噪像素往往较多，未能保持这部分像素的原始信息。针对部分方法在噪声密度较高时难以取得理想的去噪效果，Vasanth等[11]提出一种非对称修剪的几何平均算法，但是大小固定的3×3邻域，始终是其去噪效果提升的瓶颈（decision based asymmetrically trimmed modified geometric mean algorithm, DTGM）。Sharma等[12]提出一种检测和去除脉冲噪声的多层决策迭代滤波器（multilayer decision based iterative filter for removal of salt and pepper noise, MDIF），用固定大小的邻域以保持最大的相关性，基于噪声密度的有效决策在去除噪声的同时能较好地保持图像的边缘和细节。鉴于当前的红外图像降噪方法在降噪效果和细节保持上各有侧重，王加等[13]对目前主流的红外图像降噪算法进行了调研，提出了一种基于图像分层的自适应降噪算法。但是图像分层的参数选取依然是一个病态问题，缺乏理论基础。

为了去除红外图像的脉冲噪声的同时，有效保持和恢复图像的纹理细节，本文提出了一种基于灰度特征和众数原则的迭代双边中值滤波（bilateral median filter based on intensity features and mode principle, BMF）。BMF方法利用脉冲噪声的灰度特征和局部像素分布的众数原则，将噪声像素检测出来，然后针对噪声像素，用基于空间距离和灰度相似的频次加权中值作为噪声像素的估计值，以迭代遍历的方式去除高密度的噪声。主、客观的实验结果证明了本文方法的有效性和优越性。

1 基于灰度最值和众数原则的噪声检测

1.1 脉冲噪声的定义

脉冲噪声是一种随机噪声，将部分像素重新赋值为最小灰度值或最大灰度值，以破坏图像的信息。脉冲噪声对图像的破坏程度以噪声密度衡量，对于灰度级数为的红外图像，其分布服从数学模型：

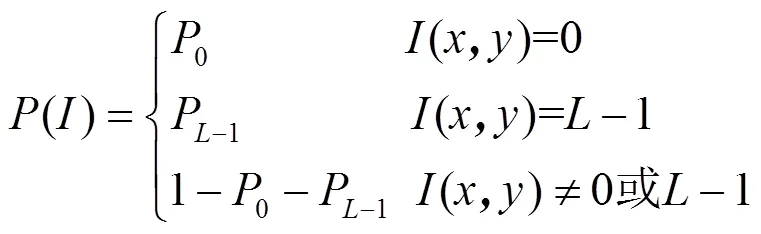
式中：(,)表示图像中处于第行、第列的像素，以下定义与此相同；( )表示概率密度函数，最小值噪声和最大值噪声的密度分别为0和P－1，因此有100×(1－0－P－1)%的图像像素未受到噪声的影响。

1.2 结合灰度特征和众数原则的噪声检测

噪声检测是为了仅对噪声像素进行去噪处理，而保护无噪像素的原始信息；检测的准确性在一定程度上决定后续去噪处理的效果。在红外图像中，会存在原本灰度值为0和－1的部分像素，根据脉冲噪声所服从的数学模型(1)可知，这部分像素与噪声像素仅从灰度取值上难以区分。因此，仅根据脉冲噪声的灰度特征进行检测会产生部分误检。所以，除了根据噪声的灰度特征进行噪声检测之外，本文进一步在邻域中利用众数原则作进一步的检测，以尽可能地降低噪声检测的误检率。

邻域像素在红外图像中具有较大的相关性，而脉冲噪声以一定的概率随机地分布于红外图像中，与邻域的无噪像素不具有相关性，且灰度差别较大。取最小值0或最大值－1的像素，如果其灰度值与当前邻域中多数像素的灰度取值相同或相近，可大概率地判断其为无噪像素，否者为噪声像素。根据以上分析，提出了基于灰度特征和邻域的众数原则的噪声检测方法。

假设图像的灰度级数为（灰度级范围为0～－1）；为大小与图像一样的噪声识别矩阵，用(,)＝0标记噪声像素而用(,)＝1标记非噪声像素；(x,y)()为以像素(,)为中心、边长为的方形邻域，噪声检测的具体步骤如下。

1）对于图像中的每一像素(,)，如果(,)＝0或(,)＝－1，令(,)＝0，否者令(,)＝1。

2）对应(,)＝0的每一像素(,)，如果(x,y)(5)中灰度为0的像素数超过，即sum((x,y)(5)＝0)＞，识别(,)为无噪像素，令(,)＝1。

3）对应(,)＝－1的每一像素(,)，如果(x,y)(5)中灰度为－1的像素数超过，即sum((x,y)(5)＝－1)＞，识别(,)为无噪像素，令(,)＝1。

4）对应(,)＝0或(,)＝－1的每一像素(,)，如果(x,y)(5)存在非最值像素，且(,)与非最值像素均值的绝对差小于，识别(,)为无噪像素，令(,)＝1。其中为(x,y)(5)中非最值像素的标准差。

对于步骤2）和3）中的阈值，经过在实验中应用试错法，确定＝20为最优。步骤1）检测出的噪声像素，包括了所有的噪声像素与取最小和最大值的无噪像素，而步骤2）～4）根据局部的众数原则将取最小和最大值的无噪像素从候选噪声中剔除，降低噪声的误检率。

2 迭代的双边中值滤波

红外图像相邻的像素，一方面具有空间邻近的相关性，即空间距离越小的像素，其之间的相关性越大；另一方面相邻像素具有灰度相似的相关性，即在灰度上差别较小的像素，其之间的相关性越大。双边滤波就是根据以上思想，利用邻域像素在空间域的相关性和像素域的相关性对当前像素进行恢复，但是其属于加权均值滤波，能有效去除高斯噪声，但是不适用于脉冲噪声。因此，本文提出迭代的双边中值滤波。

2.1 加权系数

对于每一对应(,)＝0的像素(,)，令(,)为邻域(x,y)()中的像素，基于空间距离的加权系数定义为：

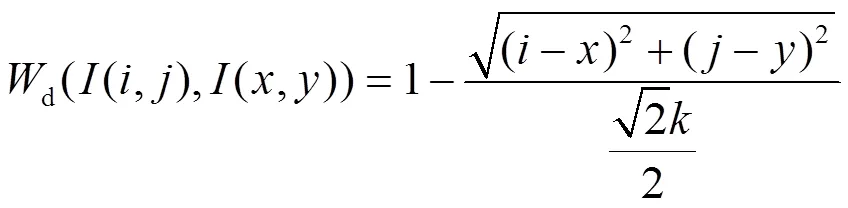
基于灰度相似的加权系数的定义如式(3)所示。

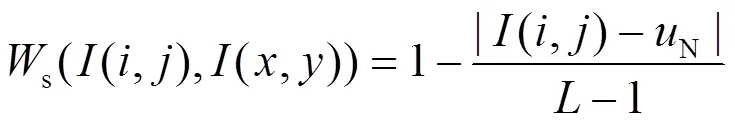
式中：－1为灰度绝对差的归一化因子；N为邻域(x,y)()中无噪像素的均值；加权系数s反比于灰度绝对差，差值越小，加权系数越大，最小系数为0，最大系数为1。

因为空间域与灰度域的量纲不一样，所以在式(2)和(3)中将其归一化处理，实现量纲的一致性。将以上两加权系数的均值作为综合空间域相关性和灰度域相关性的加权系数：

＝(d＋s)/2 (4)

特别地，的加权系数只对应邻域(x,y)()中的无噪像素，(x,y)()中噪声像素(,)对应的加权系数为0，即(,)＝0。噪声无相关性，不参与对当前噪声像素(,)的恢复。

2.2 基于加权系数的加权频次

根据中的加权系数给(x,y)()中的无噪像素(,)分配加权频次，加权频次按顺序地正比于无噪像素(,)对应的加权系数(,)，其中最小的加权系数的加权频次为1。具体方法如下。

1）分别统计中非零的元素个数、以及非零且值不同的元素个数。

＝numel(≠0) (5)

＝unique(≠0) (6)

2）将中的非零且值不同的元素升序排序，得到个元素的序列（中值相同的多个元素对应中同一个元素）。

＝{()|()＜(+1),＝1,2,…－1 } (7)

3）根据序列中的序号，按顺序地给对应权值()的无噪像素(,)赋予加权频次()：

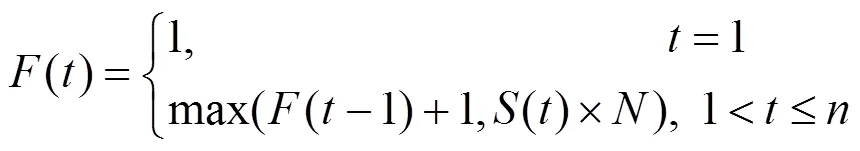
式(7)根据序列中的加权系数()分配的频次的特点为：对应最小加权系数(1)的无噪像素(,)分配的加权频次为1；其余无噪像素分配的加权频次正比于对应的加权系数()，但是至少保证对应加权系数()的加权频次比(－1)大1。合理地体现邻域(x,y)()中的无噪像素(,)对当前中心像素(,)相关性的大小。

2.3 迭代的加权中值去噪

根据式(7)分配的加权频次()，对邻域(x,y)()中的非噪声像素(,)进行复制操作，然后取中值作为当前噪声像素(,)的新灰度值，实现噪声像素的恢复：

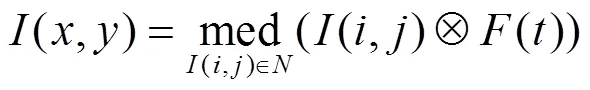
式中：med为取数列排序后的中间值的函数；Ä为复制操作符。

当脉冲噪声密度较低时，对红外图像的所有像素进行一次遍历加权中值去噪，基本上能对所有的噪声像素进行恢复。当噪声密度较高时，部分噪声像素(,)的邻域(x,y)()中的像素全被噪声破坏，没有无噪像素可以对当前的噪声像素(,)进行恢复。虽然可以通过进一步扩大邻域以包含远处的无噪像素，但是过度扩大邻域以包含进来的无噪像素与当前像素的相关性较弱，用其对当前噪声像素的灰度进行估计，可能与原始的真实值偏差较大。因此本文提出固定邻域的、迭代的加权中值去噪方法，具体步骤如下。

1）对于图像中的每一尚未恢复的噪声像素(,)，如果其邻域(x,y)(5)存在无噪像素或已经去噪恢复的像素，即对应的sum((x,y)(5))＞0，用式(8)方法对其进行恢复，且令(,)＝1。

2）重新统计噪声密度，如果噪声密度降到非常低，即sum()/numel()＜，转3），否者转1）。

3）对于图像中的每一尚未恢复的噪声像素(,)，用其邻域(x,y)(5)中的所有像素的均值作为其新的灰度值。

因为3×3邻域太小，当噪声密度较高时，其难以彻底去除噪声，而7×7邻域太大，用相关性较弱的无噪像素对噪声像素进行恢复，会产生模糊效果，因此方法中采用大小为5×5的邻域，且根据实验和经验，用5×5的邻域通过迭代足以去除密度高达90%的脉冲噪声。另外，步骤2）中的阈值设为0.01。当噪声密度较低时，迭代执行步骤1）较少的次数，便可基本上去除所有噪声；当噪声密度较高时，迭代执行步骤1）多次，便可彻底去除噪声。

3 实验结果与分析讨论

为了验证本文方法的有效性和实用性，将本文方法与部分最新提出的方法应用于图1所示的红外图像以及红外人脸数据集CBSR NIR Face Dataset，根据峰值信噪比（peak signal to noise ratio，PSNR）[14]和边缘保持指数（edge preservation index，EPI）[15]、视觉效果和计算速度对方法进行分析评价。参与实验比较的方法为AFMF[5]、DAMF[9]、DTGM[11]和MDIF[12]。

3.1 PSNR和EPI

峰值信噪比PSNR逐像素地度量两幅图像的像素相似性，去噪图像与原无噪图像的像素越相似，对应的PSNR就越大，说明去噪效果越好。边缘保持指数EPI度量去噪图像相对于原无噪图像的边缘保持和恢复的效果，边缘保持和恢复得越好，对应的EPI越大，说明去噪图像的边缘信息更丰富。

各方法应用于含各种密度噪声的场景一图像所得的PSNR和EPI值如图2所示。其中方法DAMF在噪声密度较低时，其去噪效果较好，但是随着噪声密度增大，其去噪效果骤降，PSNR和EPI值走向最小。方法MDIF的去噪效果不够理想，其PSNR和EPI较小，因为其仅根据脉冲噪声的灰度特征进行噪声检测，部分像素的原始信息未能得到保持。方法DTGM的PSNR和EPI值处于中等，其自适应的几何均值去噪方法对去噪性能的提升不明显。方法AFMF的去噪效果较好，PSNR和EPI值都较大。相对地，本文方法的PSNR和EPI值大于其他方法，其在噪声去除以及边缘细节的保持和恢复上均表现良好。

图1 实验图像

各方法对含各种密度噪声的场景二图像进行去噪所得的PSNR和EPI值如图3所示。其中，方法DTGM的PSNR和EPI值较小，其固定的3×3邻域限制了其去噪性能的提升。方法AFMF的PSNR和EPI值相对处于中下水平，而在噪声密度特别高时，其PSNR值骤然走低，其用频率中值代替自适应中值的效果不明显。方法DAMF的PSNR和EPI值均相对处于中等水平，其仅根据灰度特征的噪声检测方法限制了其对黑色背景的保持能力。方法MDIF的去噪效果相对较好，其PSNR和EPI值均较大。

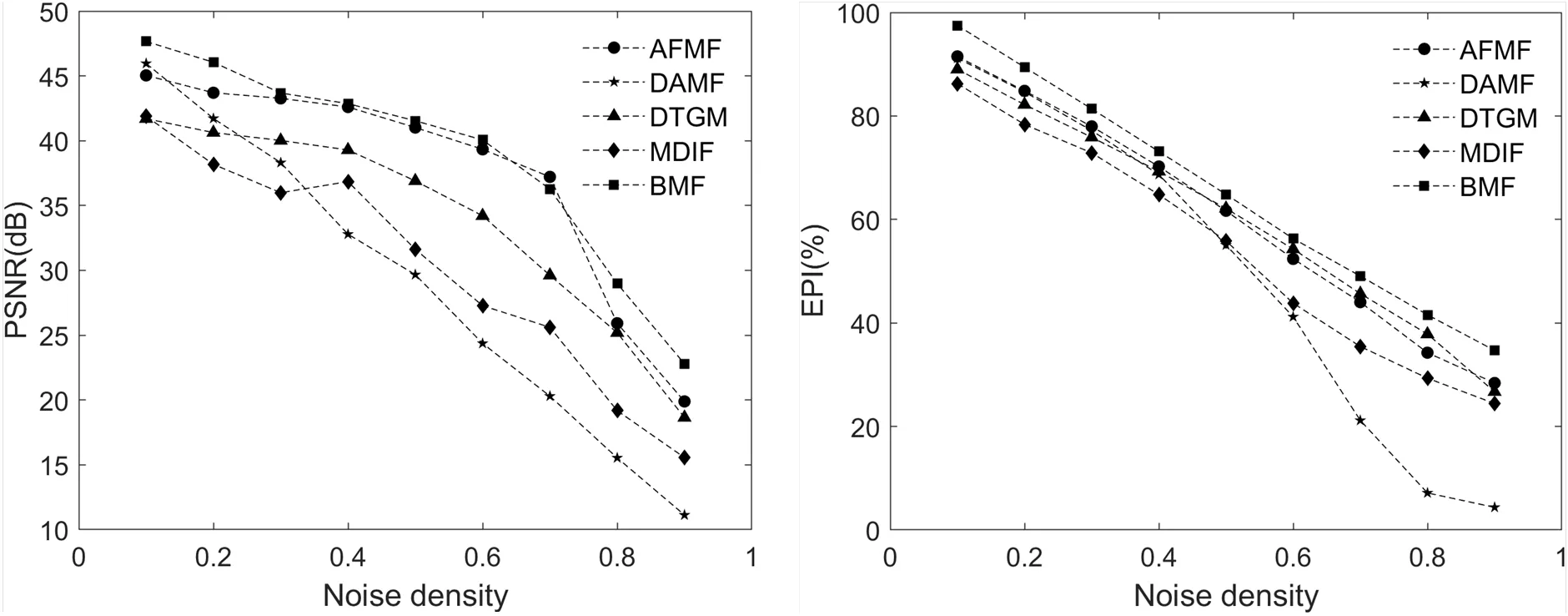
图2 各算法对含各种密度噪声的场景一的量化指标值

相对地，本文方法以最高的PSNR和EPI值，表现出优于其他方法的去噪效果，对于不同的噪声密度，其PSNR和EPI曲线始终与其他方法保持一定的差距。

对于场景三图像，其细节信息较丰富，而黑色背景的区域较少。各方法对其进行去噪所得的PSNR和EPI值如图4所示。其中，不管是低噪声密度还是高噪声密度，方法DTGM的PSNR和EPI值均小于其他方法，其在较小的邻域中采用几何均值对像素进行恢复，难以有效保持和恢复图像的边缘和细节信息。方法MDIF的PSNR值相对稍低，但是EPI值较大，图像边缘的保持和恢复能力较好。方法AFMF在逐像素的恢复和边缘信息的保持上处于中等水平，方法DAMF的PSNR值较大，EPI值大致处于中等水平。本文方法在逐像素的恢复与边缘信息的保持和恢复上均表现出优越的性能，其PSNR和EPI值均大于其他方法。

3.2 视觉效果

人眼的视觉感知能辨别噪声去除是否彻底、去噪图像是否清晰和边缘细节能否较好地恢复。鉴于低密度噪声的去除效果难以用视觉感知进行辨别，因此采用高密度噪声。各方法对含噪密度0.8的3个不同场景红外图像的去噪图像如图5～7所示。其中，为了更清晰地辨析各方法对边缘细节的恢复能力，将各去噪图像中白色小矩形的细节区域放大7倍，显示于图像的右下角。

含噪密度为0.8的场景一红外图像以及各方法的去噪图像如图5所示，其中，方法DAMF的去噪效果较差，黑色的背景被破坏，因为其噪声检测方法不能区分噪声像素与取最小和最大值的无噪像素。MDIF基本上能对噪声图像进行恢复，但是出现了异样的区域，如白色箭头所指。方法DTGM的去噪图像出现部分白色斑块，根据右下角的细节放大部分，其边缘细节略显模糊。方法AFMF的去噪效果较好，放大区域也显示出良好的边缘保持能力，但是，原图像右上角的白色区域未能较好地恢复，且增加了白色斑块。本文方法在彻底去除噪声的同时，保持较高的图像清晰度，且细节放大区域显示出其具有较好的边缘保持能力。

图3 各算法对含各种密度噪声的场景二的量化指标值

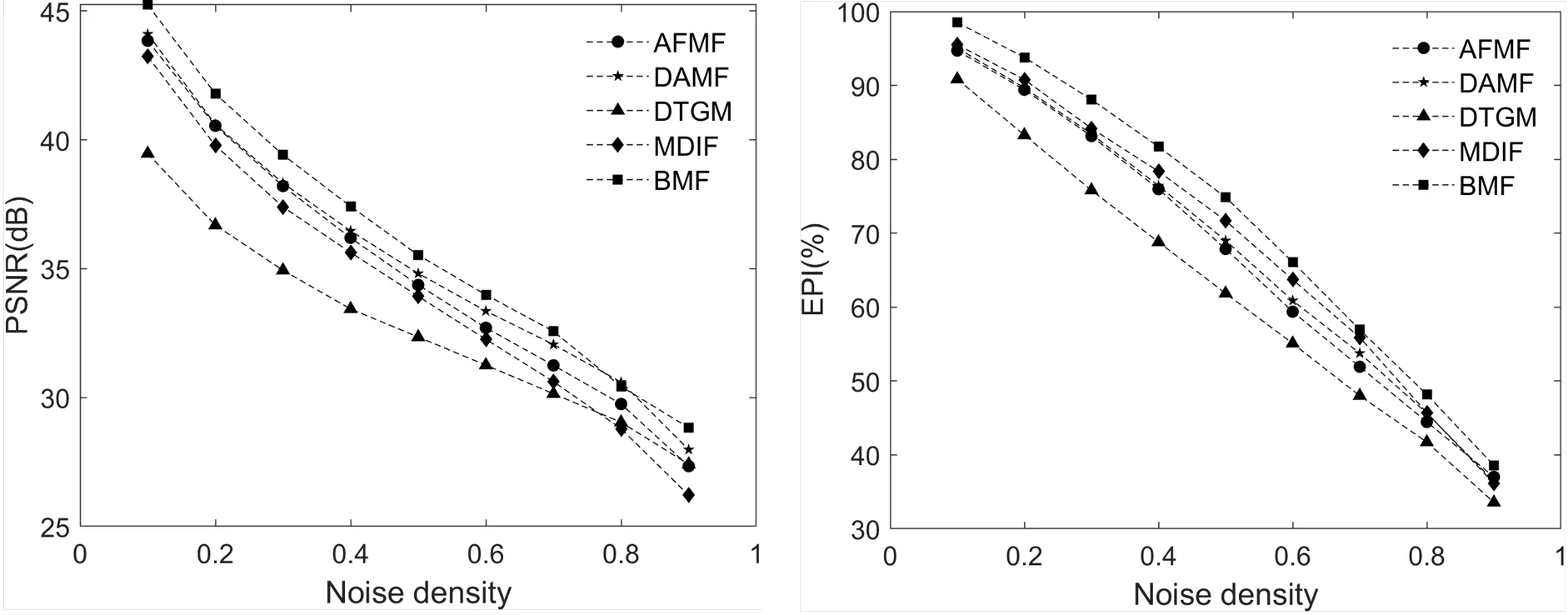
图4 各算法对含各种密度噪声的场景三的量化指标值

图5 各方法对噪声密度0.8的场景一的去噪图像

各方法对含噪0.8的场景二的去噪图像如图6所示。从噪声图像很难识别出任何的图像信息，但是各方法均能在一定程度上对其进行了去噪恢复。其中方法DTGM的边缘保持能力较差，其去噪图像的边缘较模糊，边缘线条不连续。方法AFMF的去噪图像的清晰度不高，边缘线条的锯齿效果较明显，从细节放大区域可以看出部分微小的边缘被破坏。方法DAMF和MDIF的去噪效果相对较好，两者相差不大，但是边缘线条还是有部分锯齿效果。相对地，本文方法的去噪图像较清晰，较好地恢复了图像的边缘细节，锯齿效果不明显，放大的细节区域的细节信息较丰富。

图6 各方法对噪声密度0.8的场景二的去噪图像

场景三红外图像的纹理边缘较丰富，能更好地验证去噪方法的边缘保持能力。各方法对含噪0.8的场景三的去噪图像如图7所示。方法DTGM的去噪效果较差，画面较模糊，对比度低，有雾化的效果。方法AFMF去噪不够彻底，图像上有少数的噪声斑块，从细节放大区域看，其边缘线条的锯齿效果较明显。方法DAMF和MDIF的去噪效果相差不大，均能在彻底去除噪声的同时，较好地恢复图像的纹理边缘，但是边缘线条依然有部分锯齿效果。相对于其他方法，本文方法去噪后的图像边缘线条较平滑，只有轻微的锯齿效果，画质较清晰，且根据细节放大区域可以看出，其恢复的细节信息较丰富，边缘连贯。

图7 各方法对噪声密度0.8的场景三的去噪图像

以上根据量化的图像质量指标和质化的视觉感知对各方法进行比较与分析，其中从图像质量指标与从视觉感知得出的结论基本上是一致的，结论分别如下：

1）对于不同的红外图像，本文方法在逐像素的去噪恢复和边缘细节的保持上，均优于现有的方法。

2）对于不同的红外图像，或不同的噪声密度，部分现有方法的去噪性能不稳定，对于部分图像去噪性能较好，而对其他图像较差。而本文方法对于不同的红外图像以及不同的噪声密度，均表现出一致良好的去噪性能，优于现有的方法。

3.3 计算速度

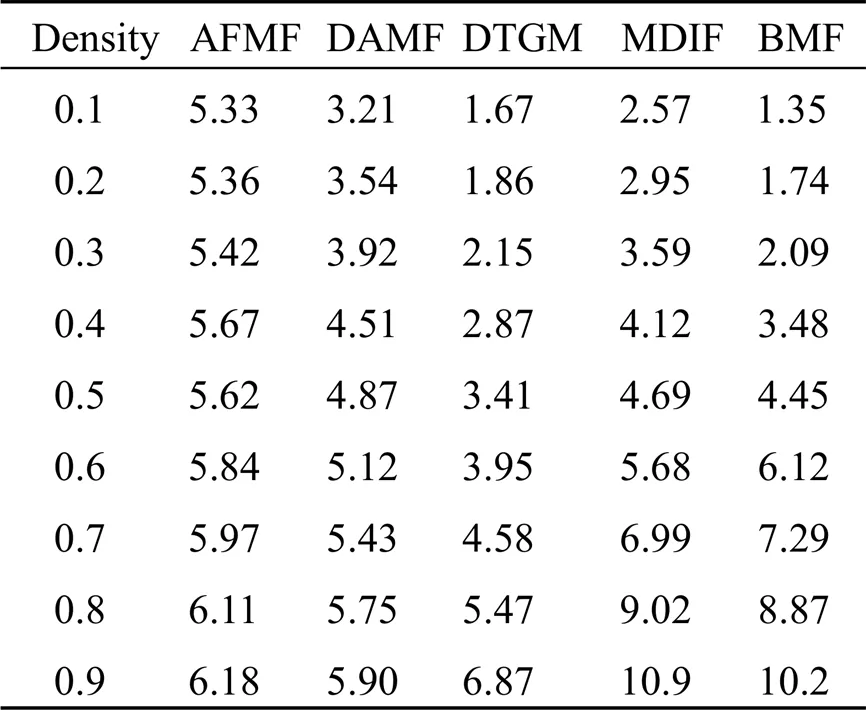
为了评价算法的实用性，在配置为i7-12700H CPU和16G内存、安装有Win10和Matlab 2021a的笔记本电脑上，将各方法用于红外人脸数据集CBSR NIR Face Dataset。各方法对数据集单张图像的平均计算时间如表1所示。

从总体上看，方法DTGM的计算速度较快，其次为方法DAMF和本文方法，方法AFMF和MDIF较慢。因为本文方法对于密度较低的噪声，用一次去噪遍历或较少次的迭代即可去除噪声，而对于密度较高的噪声，需用多次的迭代去噪遍历，才能彻底去除噪声，所以本文方法对于低密度噪声的计算速度较快，而对于高密度噪声的执行速度较慢。假设图像的像素数为，邻域大小为×，由于采用矩阵运算，本文方法的噪声检测的计算复杂度为22O()，而噪声去除处理的计算复杂度为(22＋1)O()；假设迭代次数为，本文方法总的计算复杂度为(42＋1)O()，因为≪，≪，所以近似为平方阶O(2)。本文方法的计算复杂度处于可接受的水平。

表1 各方法对数据集单张图像的平均计算时间

Table 1 Average computational time of each method for a single image of the dataset

4 结论

提出的迭代双边中值滤波方法，根据脉冲噪声的灰度和分布特征，将噪声像素检测出来，然后针对噪声像素，用基于空间的邻近度和灰度相似度的双边中值滤波进行去噪处理，以迭代遍历的方式去除高密度噪声。主、客观的实验结果均证明了提出方法的有效性和鲁棒性，相对于部分现有方法，能更有效地去除红外图像中的脉冲噪声。

[1] Khan S, Lee D. An adaptive dynamically weighted median filter for impulse noise removal[J]., 2017, 2017(1): 1-14.

[2] Erkan U, Gökrem L. A new method based on pixel density in salt and pepper noise removal[J]., 2018, 26(1): 162-171.

[3] Balasubramanian G, Chilambuchelvan A, Vijayan S, et al. An extremely fast adaptive high performance filter to remove salt and pepper noise using overlapping medians in images[J]., 2016, 64(5): 241-252.

[4] ZHANG Z, HAN D, Dezert J, et al. A new adaptive switching median filter for impulse noise reduction with pre-detection based on evidential reasoning[J]., 2018, 147(2018): 173-189.

[5] Erkan U, Serdar E, Thanh D, et al. Adaptive frequency median filter for the salt and pepper denoising problem[J]., 2020, 14(7): 1291-1302.

[6] SHAO C, Kaur P, Kumar R. An improved adaptive weighted mean filtering approach for metallographic image processing[J]., 2021, 30(1): 470-478.

[7] 徐超, 冯辅周, 闵庆旭, 等. 基于形态学和OTSU算法的红外图像降噪及分割[J]. 红外技术, 2017, 39(6): 512-516.

XU C, FENG F, MIN Q, et al. Infrared image denoising and segmentation based on morphology and Otsu method[J]., 2017, 39(6): 512-516.

[8] LIU N, YANG C, CAO H. Noise suppression of the reconstruction of infrared digital holography based on pyramid-based bilateral filter[J]., 2017, 85: 352-358.

[9] Goel N, Kaur H, Saxena. Modified decision based unsymmetric adaptive neighborhood trimmed mean filter for removal of very high density salt and pepper noise[J]., 2020, 79: 19739-19768.

[10] 顾雅青, 葛宾, 高晨. 基于模糊滤波器的钢水红外图像混合噪声处理[J]. 红外技术, 2019, 41(7): 623-627.

GU Y, GE B, GAO C. Fuzzy filter-based mixed noise processing for molten steel infrared image[J]., 2019, 41(7): 623-627.

[11] Vasanth K, Ravi C, Nagaraj S, et al. A decision based asymmetrically trimmed modified geometric mean algorithm for the removal of high density salt and pepper noise in images and videos[J]., 2021, 225(2021): 147-154.

[12] Sharma N, Sohi P, Garg B, et al. A novel multilayer decision based iterative filter for removal of salt and pepper noise[J]., 2021, 80(17): 26531-26545.

[13] 王加, 周永康, 李泽民, 等. 非制冷红外图像降噪算法综述[J]. 红外技术, 2021, 43(6): 557-565.

WANG J, ZHOU Y, LI Z, et al. A survey of uncooled infrared image denoising algorithms[J]., 2021, 43(6): 557-565.

[14] Enginoğlu S, Erkan U, Memiş S. Adaptive cesáro mean filter for salt-and-pepper noise removal[J]., 2020, 7(1): 304-314.

[15] CHEN J, ZHAN Y, CAO H. Adaptive sequentially weighted median filter for image highly corrupted by impulse noise [J]., 2019, 7(2019): 158545-158556.

Iterative Bilateral Median Filter Based on Intensity Features and Mode Principle

ZHONG Wen，LUO Qiqiang

(,,330108,)

In order to effectively maintain and restore the edges and details of infrared images while removing the impulse noise, an iterative bilateral median filter based on intensity features and mode principle is proposed. In this method, based on the intensity features of impulse noise and the mode principle, the pixels that take the minimum and maximum values and are isolated on the intensity distribution of the neighborhood are recognized as noisy pixels. According to the weighted coefficients with respect to the spatial distance and intensity similarity, the noiseless pixels in the neighborhood and the pixels that have been denoised and restored are weighted by the frequencies, and the frequency weighted median is used as the estimated value of noisy pixels. Furthermore, the denoising processing is performed in the way of iterative traversal processing, which makes the most of the results of the previous traversal processing to remove high density noise. The experimental data confirm that the PSNR and EPI values and the visual effects achieved by the proposed method are better than the existing methods, with better denoising performance.

impulse noise, infrared image, weighted frequency, bilateral median filter, EPI

TP391

A

1001-8891(2023)12-1330-07

2022-09-14；

2023-02-28.

衷文（1984-），男，江西万安人，硕士，副教授，研究方向为计算机图形学与智能软件，E-mail: 65141955@qq.com。

罗启强（1980-），男，江西贵溪人，硕士，副教授，研究方向为图像处理与信息系统项目。

国家自然科学基金（61562063）；江西省教育厅科学技术研究项目（GJJ212517）。