考虑多台区互联的中低压交直流混合配电网双层协同优化调度方法
刘科研,盛万兴,詹惠瑜,佟博,张璐,唐巍
(1.中国电力科学研究院有限公司配电技术中心,北京市 100192;2.中国农业大学信息与电气工程学院,北京市 100091)
0 引 言
高比例分布式电源(distributed generation,DG)和新型用电设备接入配电网,给传统配电网的安全运行带来更多挑战。光伏、电动汽车等设备在促进能源清洁化的同时,也会带来电压越限、功率波动等问题[1]。随着电力电子技术的发展,交直流混合配电网将成为新型电力系统的重要组成部分[2]。与传统交流配电系统相比,交直流混合配电系统打破了配电网辐射状运行的壁垒,其功率控制更为灵活[3-4],在高比例分布式电源和不确定性负荷接入的场景下具有更大的优势[5]。随着源荷设备的增加,中低压交互、多台区互联的交直流混合配电网得到多越来越多的关注,如何实现台区内的功率自治和台区间的协同功率优化,成为亟需解决的问题。
目前,对于交直流混合配电网的功率优化问题,已经有了较为成熟的研究。文献[6]考虑配电网电压变化,及其在安全约束下与储能经济运行策略间影响关系,提出了一种配合降压变压器及电压源型换流器(voltage source converter,VSC)调压的含储能交直流配电网日级别经济运行优化方法。文献[7]通过二阶锥松弛将交直流配电网稳态潮流约束转化为二阶锥形式,进而提出了基于二阶锥规划的多时段日前优化调度模型。文献[8]建立了考虑风电不确定性的交直流配电网分布式优化运行模型,并搭建典型的交直流混合配电网结构和分布式优化框架。文献[9]以交直流配电网向上级电网购电成本和系统运行成本最小为目标,建立了交直流配电网储能与换流站协调经济调度模型。文献[10]以配电网主体盈利最大为目标函数,考虑DG接入、电容器组投切、储能充放电调节、电价型需求响应、VSC运行以及网络重构等多种约束,建立了基于数据驱动的交直流配电网分布鲁棒优化调度模型。为有效适应交直流配电网分布式光伏和负荷不确定性波动带来的电压安全问题,文献[11]提出了一种计及交直流配电网电压风险感知的优化调度方案。
然而,现有研究中大多针对单一交流和直流线路互联的情况进行功率优化,对于多台区、多电压等级的交直流配电网功率交互研究尚不充分。文献[12]计及分布式电源和负荷的不确定性建立源荷概率分布模型进行随机潮流计算,并提出一种免疫混沌杂交粒子群优化算法用于求解交直流配电网电压优化模型。但其只考虑了单一电压等级下一交一直互联的情况,并未分析多台区互联的场景。文献[13]将含柔性变电站的交直流配电网系统解耦为中压交流子系统、中压直流子系统、低压交流子系统、低压直流子系统和柔性变电站子系统等可独立优化调度的子系统,并建立各子系统的二阶锥优化调度模型,但锥转化要求目标函数必须为支路电流的增函数,因此目标函数仅考虑了运行成本,并未考虑源荷不确定性造成的电压波动问题。文献[14]计及风电和光伏出力在空间上的相关性,提出基于场景分析法的优化调度模型,并提出基于二阶锥松弛技术和线性逼近法的逐次凸逼近规划模型进行求解,然而其并未考虑电动汽车等灵活性负荷的特点,且未计及储能在交直流配电网中发挥的重要作用。综上所述,对于多电压等级、多台区互联的交直储混合配电网优化调度,仍是需要进一步研究的问题。
针对上述不足,本文提出考虑多台区互联的中低压交直流混合配电网功率双层协同优化调度方法。将交直流配电网功率优化问题分为中压上层优化和低压下层优化问题。其中,下层低压台区内功率优化调度模型以运行成本最小为目标,得到各个区域内储能和电动汽车充放电策略;上层中压优化调度模型以系统综合电压偏差最小、综合运行成本最小为目标,得到互联换流器的功率交换方案。上、下层之间以功率和电压作为耦合变量进行交互,并以此进行迭代优化直至中压系统和各个低压子系统全部收敛。上、下层分别采用多目标遗传算法和二阶锥优化方法进行求解。最后,通过算例验证所提方法在多台区互联交直流系统功率优化中的有效性。
1 多台区互联的中低压交直流混合配电网
“双碳”目标下,为提高可再生能源消纳率和系统运行经济效益,含高比例新型源荷设备的交直流混合配电网将成为配电系统的新发展趋势,中低压协调、多台区互联的新型配电网结构得到越来越多的关注。交直流配电网功率调控手段灵活,特别是在接入光伏、储能、电动汽车等设备后,源网荷储间的功率协调成为亟需研究的问题。因此,本文对多台区互联的中低压交直流混合配电网进行双层协调优化调度,以提高系统的经济性和可再生能源消纳能力。
1.1 多台区互联的交直流混合配电网结构
多台区互联的中低压交直流配电网结构如图1所示,其中A、B、C为3个低压台区,A、C为直流台区,B为交流台区,共同接在中压交流10 kV线路上。3个台区接有光伏、电动汽车、5G基站、储能等不同特性的源荷设备,台区之间通过交直流换流器互联,可实现功率的转供。
上述交直流混合配电网中,低压台区内包含分布式光伏(photovoltaic,PV)、电动汽车(electric vehicle,EV)、储能(energy storage system,ESS)、5G基站(5G base station,BS)等设备,其中独立储能系统和基站备用储能系统均可作为可调度电源,电动汽车可通过V2G(vehicle to grid)技术参与电网调度。光伏发电电能一方面可直接用作负荷供电,另一方面可通过储能进行存储。系统的调度框架如图2所示。
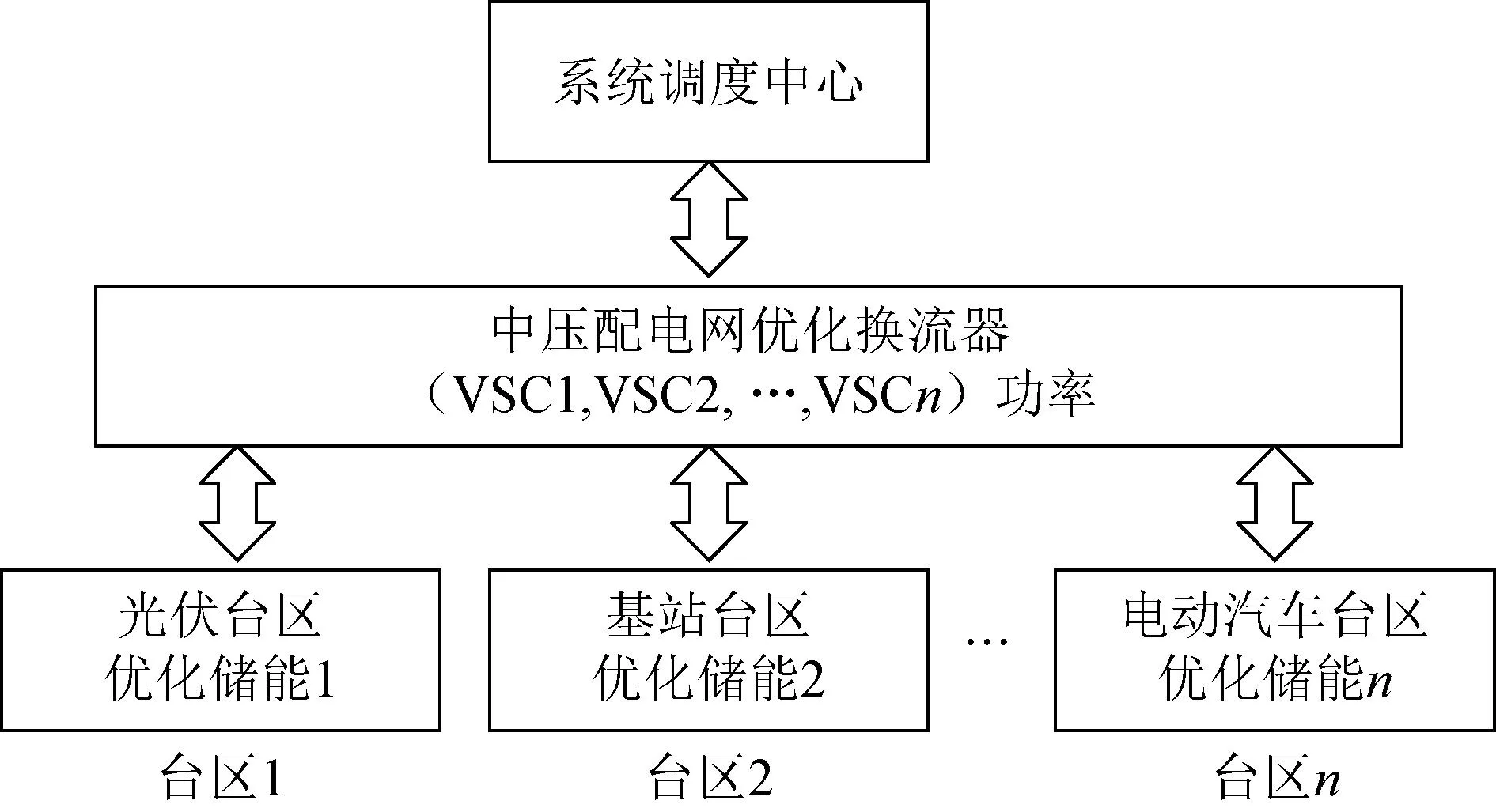
图2 系统调度框架Fig.2 System scheduling framework
如图2所示,调度中心收集中压系统和低压系统的负荷分布情况及系统运行参数,首先针对各个台区的源荷特性,优化低压台区的储能充放电策略和电动汽车V2G策略,实现低压层的各个子区域功率优化。其次,收集中压台区的负荷情况和运行参数,并将各个低压台区的优化参数作为已知量,共同参与中压层各个换流器的功率优化。完成第一轮优化计算后,中压优化结果中的节点电压和注入功率值,将传递给各个低压台区,进行子区域的第二轮优化,以此进行迭代直至收敛或达到最大迭代次数。
1.2 多台区互联的中低压交直流配电网分析与建模
1.2.1 低压台区分析及建模
1)分布式光伏。
光伏通过光伏阵列将太阳能转化成电能,其输出功率和光照强度近似满足线性关系,假设太阳能光伏阵列有M个电池组件,每个组件的面积和光电转换效率为Am和ηm(m=1,2,…,M),则太阳能光伏阵列总输出功率PPV表达式为[15]:
PPV=rAη
(1)
式中:A、η分别为光伏阵列总面积和光伏电池板的光电转换效率;r为光照强度。
若光伏直接接在直流线路上,则无需逆变设备,若接在交流线路,则需满足逆变器容量约束:
(2)
式中:Pinv、Qinv分别为逆变器输出的有功功率和无功功率;Sinv为逆变器容量。
2)储能。
图1所示结构中,共有3处位置装有储能设备。光伏台区的储能用作储存光伏电能,5G基站所在台区的储能用作基站的备用电源,同时可参与电网调度,电动汽车充电桩所在台区的储能可供给电动汽车负荷充电。储能设备应满足充放电容量约束:
(3)
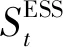
此外,还应满足充放电功率限值约束:
(4)

3)5G基站。
5G基站作为新基建背景下的新型负荷,其用电功率与区域的通信负载密切相关,根据爱立信公司测试结果,5G基站用电负荷与通信负载近似呈一次线性关系[16]:
Pb=ab+βbTb
(5)
式中:Pb为基站用电负荷;Tb为基站通信负载;ab、βb为常系数。
基站供电量应满足通信需求约束:
(6)
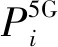
4)电动汽车。
由于电动汽车的充放电具有随机性,因此电动汽车参与V2G调度,需要对其负荷分布进行刻画。用户行为特性是影响电动汽车功率需求的关键因素,包括日行驶里程、出行开始和结束时刻。日行驶里程能反映出车辆行驶一天所消耗的电能,一般认为出行结束时刻即为车辆的开始充电时刻。
日行驶里程满足对数正态分布,其概率密度函数fLD为:
(7)
式中:μD为日行驶里程的期望值;σD为日行驶里程的标准差;x为日行驶里程。
以用户在最后一次出行结束后的时刻作为开始充电时刻,出行开始时刻的概率密度为:
(8)
式中:μe为充电开始时刻的期望值;σe为充电开始时刻的标准差;xe为充电开始时刻。充电持续时间与日行驶距离和百公里耗电量有关,计算表达式为:
(9)
式中:T为充电时长;W为车辆百公里耗能;Pc为充电功率。
台区内任一时刻的充电负荷,即为该时刻在桩充电的电动汽车数量乘以充电功率。根据建模结果,即可得到电动汽车负荷的概率分布情况,从而为V2G调度提供参考。
1.2.2 中压配电网分析及建模
中压配电网主要对各个互联换流器的传输功率进行优化,本文采用电压源型换流器,换流器可实现交直流变换,其单相结构如图3所示。为便于表述,本文规定从交流侧流向直流侧为功率正方向。

图3 电压源型换流器结构Fig.3 Topology of VSC
图3中:Us∠θs为交流网络侧母线S处电压;Uc∠θc为换流器交流侧母线C处电压;Yt为换流器复合导纳,表征变压器等效导纳和换流器等值导纳。交流网络母线S处的注入功率Ps和Qs为:
(10)
式中:Gt为换流器复合电导;Bt为换流器复合电纳;Δθsc=θs-θc。
换流器交流侧C处的注入功率Pc、Qc为:
(11)
在VSC直流侧,VSC注入直流网络的有功功率Pc,dc为:
Pc,dc=Pc-Pc,loss
(12)
式中:Pc,loss为换流器的损耗功率。采用广义换流器损耗计算模型:
(13)
(14)
式中:Ic为VSC交流侧电流,由交流侧流向VSC为正方向;SN为VSC的额定容量;Ud为直流侧电压;Uc为VSC交流侧电压。
2 多台区互联的中低压交直流配电网优化调度模型
为提高中低压交直流混合配电网的运行经济性并降低系统的电压波动,实现中低压交直流配电网的协同优化,本文建立双层优化模型,以节点电压和功率作为交互变量,通过上层中压模型和下层低压模型迭代求解,直至中低压系统均达到收敛,实现中压系统和各个低压子系统的全局优化。
2.1 低压台区功率优化调度模型
低压台区功率优化以系统综合成本最小为目标,成本主要包括购电成本、弃光成本、网络运行损耗成本和储能调度成本。目标函数可表示为:
minClow=Cpur+CPV+Closs+CESS+CEV
(15)
式中:Clow为低压台区总成本;Cpur为向上级电网购电成本;CPV为光伏弃光成本;Closs为交直流系统运行损耗成本;CESS为储能充放电成本;CEV为调度电动汽车放电成本[17]。各个成本计算公式为:
Cpur=ωtEt
(16)
CPV=ωPVEPV
(17)
Closs=ωtPloss,t
(18)
(19)
CEV=ηEV1PEV+ηEV2NEV
(20)
式中:ωt为t时刻的电价;Et为t时刻向上级电网的购电量;ωPV为光伏补贴电价;EPV为弃光电量;Ploss,t为t时刻网损;nESS为调度周期内储能充放电次数;NESS为储能寿命内允许的总充放电次数;Cinv为寿命内的储能投资成本;ηEV1为调度电动汽车单位功率的电量补偿成本;PEV为参与调度的总功率;ηEV2为改变用户充电行为的补偿成本[18];NEV为参与调度的电动汽车总数。系统运行损耗成本又包括交流系统损耗成本、直流系统损耗成本。
Ploss=Ploss,AC+Ploss,DC+Ploss,VSC
(21)
(22)
式中:Ploss,AC为交流网络功率损耗;Ploss,DC为直流网络功率损耗;Ploss,VSC为VSC功率损耗;NAC为系统中交流网络的节点数;NDC为系统中直流网络的节点数;Ω(i)为节点i相邻节点的集合;rij,AC为交流支路ij的电阻;rij,DC为直流支路ij的电阻;Iij,AC为流过交流支路ij的电流值的平方;Iij,DC为流过直流支路ij的电流值的平方。
约束条件主要包括1.2节中设备运行约束,此外还应包括电网安全运行约束:
(23)
式中:Pac,i、Qac,i分别为交流系统节点i注入的有功功率和无功功率;Gac,ij、Bij、θij分别为交流系统节点i和节点j之间的电导、电纳和电压相位差;Uac,i、Uac,j分别为节点i和节点j的电压幅值;Pdc,i为直流系统节点i的注入有功功率;Udc,i、Udc,j分别为直流系统节点i和节点j的电压幅值;Gdc,ij为直流系统节点i和节点j之间的电导。
且节点电压、支路功率应满足限制约束:
Umin≤Ui≤Umax
(24)
Pmin≤Pij≤Pmax
(25)
2.2 中压配电网功率优化调度模型
中压交直流配电网优化调度以系统综合电压偏差最小,综合成本最小为目标,优化变量为各个换流器的有功功率和无功功率。目标函数可表示为:
(26)
(27)
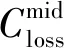
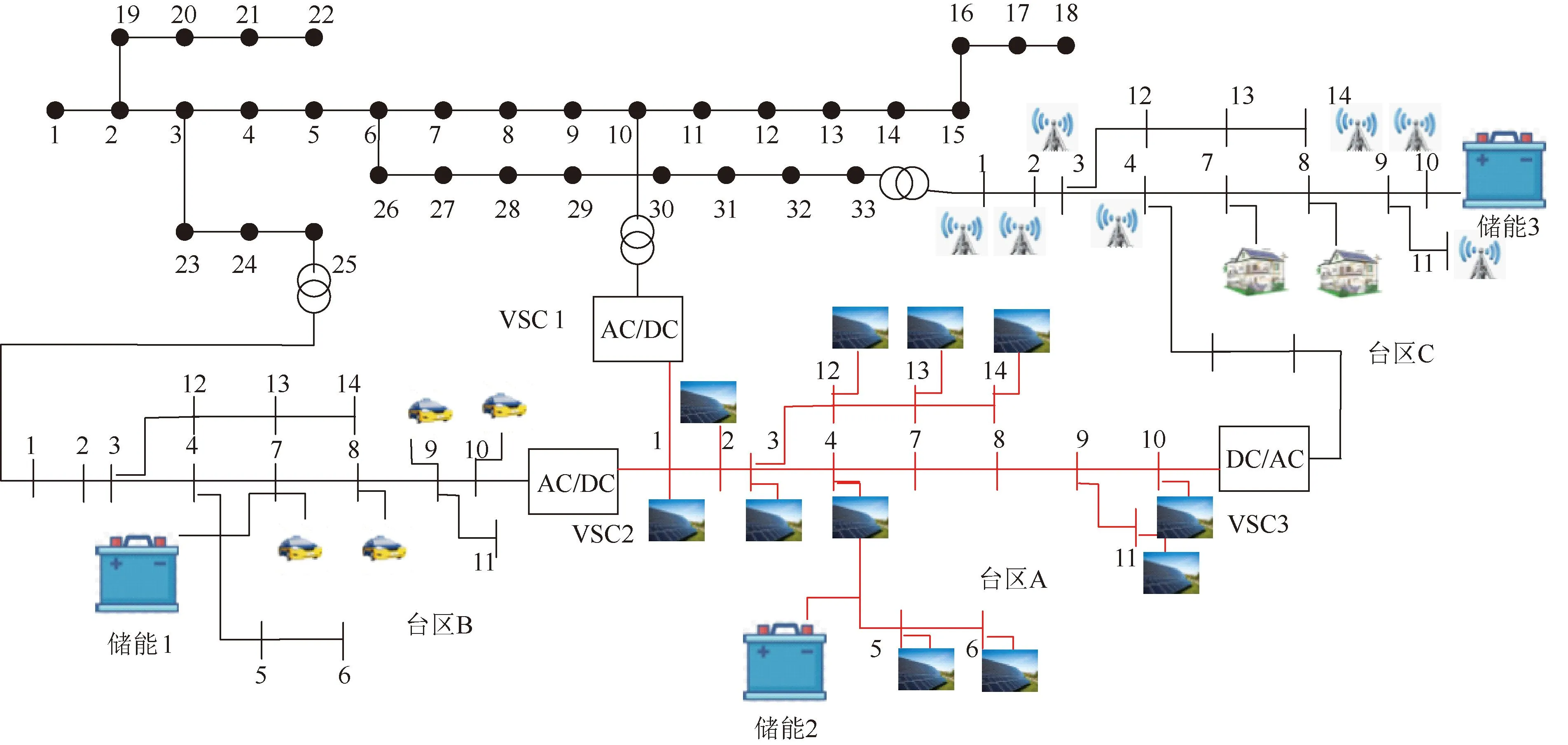
约束条件有换流器运行约束:
(28)
此外,还有式(23)—(25)所示的电网安全运行约束。
3 求解方法
3.1 中压配电网功率优化调度模型
多目标问题的数学模型可表示为:
(29)
式中:Ψ为决策变量的可行域;fm(x)为第m个目标函数。对于任意2个决策变量x1和x2,若求解问题为最小化问题,那么当且仅当满足式(30)时,称x1支配x2[19-20]。
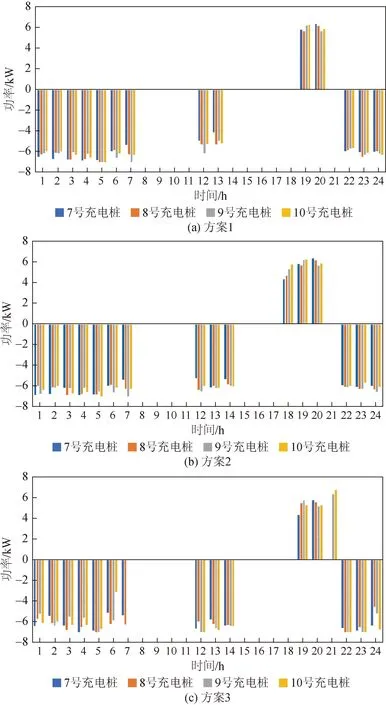
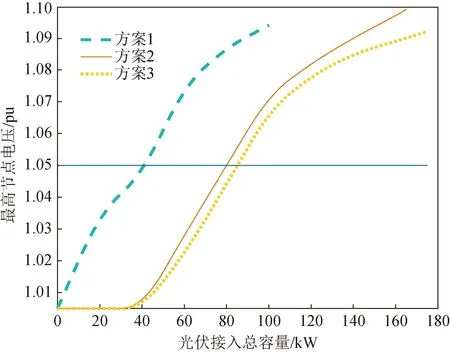
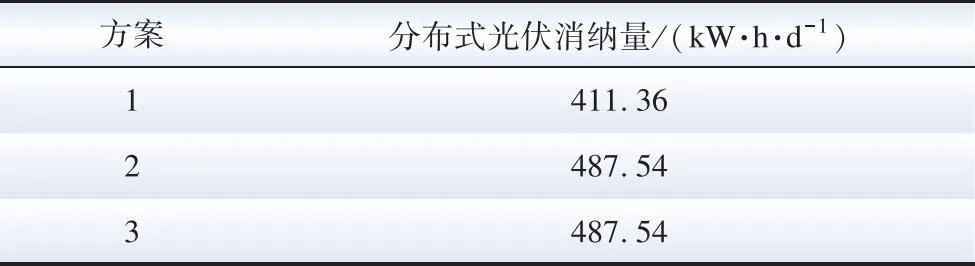
fm(x1) (30) 若对于决策变量xa∈Ψ,其不被解空间内的任意解支配,则称xa∈Ψ为该多目标问题的非劣解或Pareto最优解。所有Pareto最优解对应的目标函数向量集合称为Pareto前沿。因此,求解多目标问题的本质是找到Pareto前沿,并在其中选取最优解[21-22]。 由于各目标函数相互制约、相互竞争、没有可比较性,所以需要在Pareto最优解集中找到一组折中解作为最优结果。本文采用对所有目标函数均衡考虑的决策方法将各个Pareto最优解对应的多个目标函数值转化为单个进行比较。一个Pareto最优解每个目标适应度函数计算公式为[23-24]: (31) 式中:fi,j为第i个Pareto最优解的第j个目标函数值;fmax,j和fmin,j分别为Pareto解集中第j个目标函数的最大值和最小值。对于第i个Pareto最优解,其标准化适应度函数为[25-26]: (32) 式中:Q为目标函数的维度。 采用交替迭代的方法对上述双层模型进行求解,上、下层通过边界变量P、Q、V进行耦合。首先对低压配电网优化问题求解,得到下层问题的初始最优解,将下层求得的低压配电网状态变量返回上层。中压配电网以下层运行状态作为已知量,进行上层优化。上述模型的求解流程如图4所示。 图4 模型求解流程Fig.4 Flow chart of model solution 本文采用IEEE 33节点中压算例系统和14节点低压算例系统作为仿真背景,网络结构如图5所示。其中,中压系统电压等级为12.66 kV,低压系统电压等级为380 V。设定中压系统中的节点10、25、33分别为光伏、电动汽车、5G基站接入的台区,节点10为直流台区A,节点25、节点33为交流台区B和C。交直流台区之间通过换流器进行互联,VSC额定容量均为100 kV·A。A台区中,除普通负荷外,光伏分别接入在节点1—5、节点10—14,每个节点光伏额定功率为5 kW,具体出力可根据式(1)进行计算;储能集中配置在节点5,最大容量为100 kW·h,最大充放电功率为40 kW,充放电效率为0.9;台区B中,电动汽车充电桩接在节点7—10,单台充电桩额定功率为7 kW,储能安装在节点7,参数设定同台区A;台区C中,5G基站安装在节点1—4、节点9—11,功率按照与通信负载的关系计算,储能安装在节点10,参数设定同上。 图5 算例拓扑Fig.5 Topology of case study 采用数学优化软件Matlab R2016a作为平台对本文所提方法进行验证。硬件环境为英特尔四核i5-1155G7.4.5 GHz。遗传算法采用二进制编码方式对换流器功率进行编码,设定种群最大迭代次数Tmax为100,种群总数Pop为100,交叉变异率为0.8,收敛精度ε为0.01。 中压配电网总基础负荷见附录表A1,夏季典型日台区A、B、C的光伏、电动汽车、5G基站、居民负荷的出力曲线如图6所示。低压台区电价如表1所示。 表1 台区电价情况Table 1 Electricity price of courts 图6 光伏和负荷曲线Fig.6 PV and load curve 为验证本文所提方法在降低系统运行成本、平抑电压波动和提高可再生能源消纳率方面的有效性,设置3种优化方案进行对比分析: 方案1:中低压系统分别进行优化调度,且低压台区之间无互联; 方案2:中低压系统分别进行优化调度,低压子系统之间通过换流器连接,可进行功率交互; 方案3:中低压系统协同优化调度,低压子系统之间通过换流器连接,可进行功率交互,且中压系统可根据低压系统进行功率分配调整。 4.2.1 系统调度结果分析 不同方案下,各个台区储能的充放电情况如图7所示。 图7 储能充放电策略Fig.7 Energy storage charging and discharging strategy 7号充电桩电动汽车的调度方案如图8所示,其余充电桩充放电情况及数据见附录图A1。 图8 7号充电桩电动汽车调度方案Fig.8 EV charging and discharging strategy of No.7 charging station 不同方案下,各个换流器流过的功率情况如图9所示。 图9 VSC功率流动情况Fig.9 Power flow of VSC 对比上述调度结果可以看出,方案1不考虑低压台区之间的功率转供,无法实现台区之间的源荷互补。 对于接入大量光伏的台区A,正午时刻光伏大发,然而由于缺少功率转移途径,尽管方案1的储能在12:00的充电功率达到25.65 kW,仍然无法通过本地负荷和储能完全消纳光伏功率,导致换流器1出现了功率返送。方案2通过换流器实现低压台区间的互联,在正午光伏无法消纳的时段,可通过换流器2、3进行功率转供,既实现了台区A的光伏消纳,同时可以供给台区B、C的负荷。然而方案2未考虑中低压之间的交互,中压配电网无法根据低压台区情况调整换流器功率,台区互补的优势无法得到充分发挥。方案3通过中低压协同进行优化,储能和电动汽车的调度方案与换流器的交互功率得到了有效配合,充分实现了源荷互补。 4.2.2 系统运行经济成本分析 不同方案下低压台区各项成本情况如表2所示。中压配电网网络损耗及电压偏差情况如表3所示。 表2 不同方案成本对比Table 2 Comparision of total cost under different cases 表3 中压配电网损耗及电压偏差对比Table 3 Power loss and voltage deviation of mid-voltage distribution network under different cases 由上述结果可知,方案1台区间无功率转供,会造成76 kW的光伏资源浪费,从而导致台区总体向上级电网购电的成本增加,且由于光伏所在台区的电压升高,造成系统综合电压偏差较大;方案2考虑台区互联,将光伏功率充分用于其他台区的负荷供电,使低压总调度成本降低了29.6%,同时网络损耗降低了22.1%;方案3在通过低压台区互联提高光伏消纳能力的同时,中低压调度策略之间可以实现灵活协调,尽管电动汽车调度成本略微增加,但低压总调度成本降低了31.4%,中压网络损耗降低了26.3%,有效提高了系统的经济效益。 4.2.3 系统电压分析 不同方案下,系统在典型日内的峰谷差如表4所示。3种方案下,中压配电网在调度日内的电压分布如图10所示。 表4 不同方案峰谷差Table 4 Peak valley difference under different cases 图10 节点电压分布情况Fig.10 System node voltage 由表4可知,相较于调控前和方案1,方案3的峰谷差分别降低了25.42%和22.51%。由不同方案的电压分布结果可知,方案1由于缺乏光伏消纳手段,在正午光伏大发时刻,节点10的电压标幺值达到了1.076 pu,节点11的电压标幺值达到1.073 pu,均超过了电压上限,且系统电压波动明显。方案2通过换流器进行功率转供,使得正午时刻的光伏功率得以转供给其他台区,节点10和节点11电压分别降至1.025和1.021 pu,然而由于中低压之间缺乏交互导致不同电压等级的调控手段难以实现有效配合,系统电压仍存在较大波动。方案3通过中低压协同优化,有效降低了光伏台区所在节点的电压,系统最高电压值相对方案1降低了5.85%,且系统电压综合偏差相较方案1降低了25.53%。 4.2.4 可再生能源消纳能力分析 台区A作为光伏接入台区,其光伏消纳能力除了受到本台区负荷水平限制,同时也受到网架结构限制。以台区A最高节点电压不超过上限值作为约束,计算不同调度方案下台区A可接入的光伏最高比例,结果如图11所示。 图11 分布式光伏接入情况Fig.11 PV access capacity 典型日内分布式电源的消纳总量如表5所示。 表5 分布式光伏消纳总量Table 5 PV absorption of different cases 由表5可知,相较于方案1的各自单独调控,方案3中低压交直流协调优化使得分布式光伏消纳总量提高了18.47%。此外,对于可接入的分布式光伏总量而言,由图11可知,方案1由于台区之间无互联,缺乏功率转供手段,当光伏接入总量达到40 kW时,低压台区A最高节点电压即达到上限值1.05 pu。而方案2考虑低压台区互联,方案3进一步实现中低压之间的交互协调,光伏接入最大容量分别达到80 kW和85 kW。在方案3的调度策略下,相较于方案1,分布式电源最大接入量提高了112.5%。可见本文所提调度策略可有效提高光伏消纳能力。 本文考虑分布式光伏、储能、电动汽车等源荷设备接入中低压交直流配电网,提出了考虑多台区互联的中低压交直流混合配电网双层协同优化调度方法,低压台区以综合成本最小为目标建立交直流配电网子区域内功率优化调度模型;中压配电网以系统综合电压偏差最小、综合运行成本最小为目标,建立交直流配电网区域间优化调度模型。最后通过改进的IEEE 33节点算例系统对方法进行了验证,结果表明,中低压配电网的协同优化策略可充分发挥低压台区柔性互联的优势,并通过影响中压配电网的功率分配实现中低压迭代优化,从而减小系统网络损耗,降低电压波动。未来,随着中低压交直流配电网规模的进一步扩大,越来越多的可再生能源和新型负荷将接入配电网,如何计及源荷功率的不确定性进行复杂交直流系统的功率优化,将是未来重要的研究方向。 附录A 图A1 不同方案电动汽车充放电调度结果Fig.A1 The schedule results of electric vehicle charging and discharging under different cases 表A1 中压配电网线路参数及基础负荷Table A1 Line parameters and basic load of medium voltage distribution network3.2 中低压交直流配电网优化求解步骤

4 算例分析
4.1 算例背景
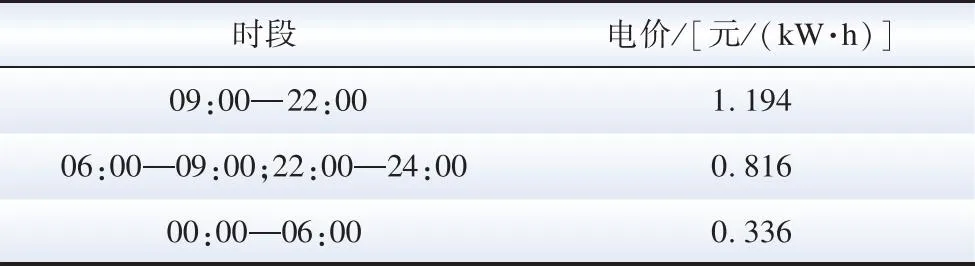
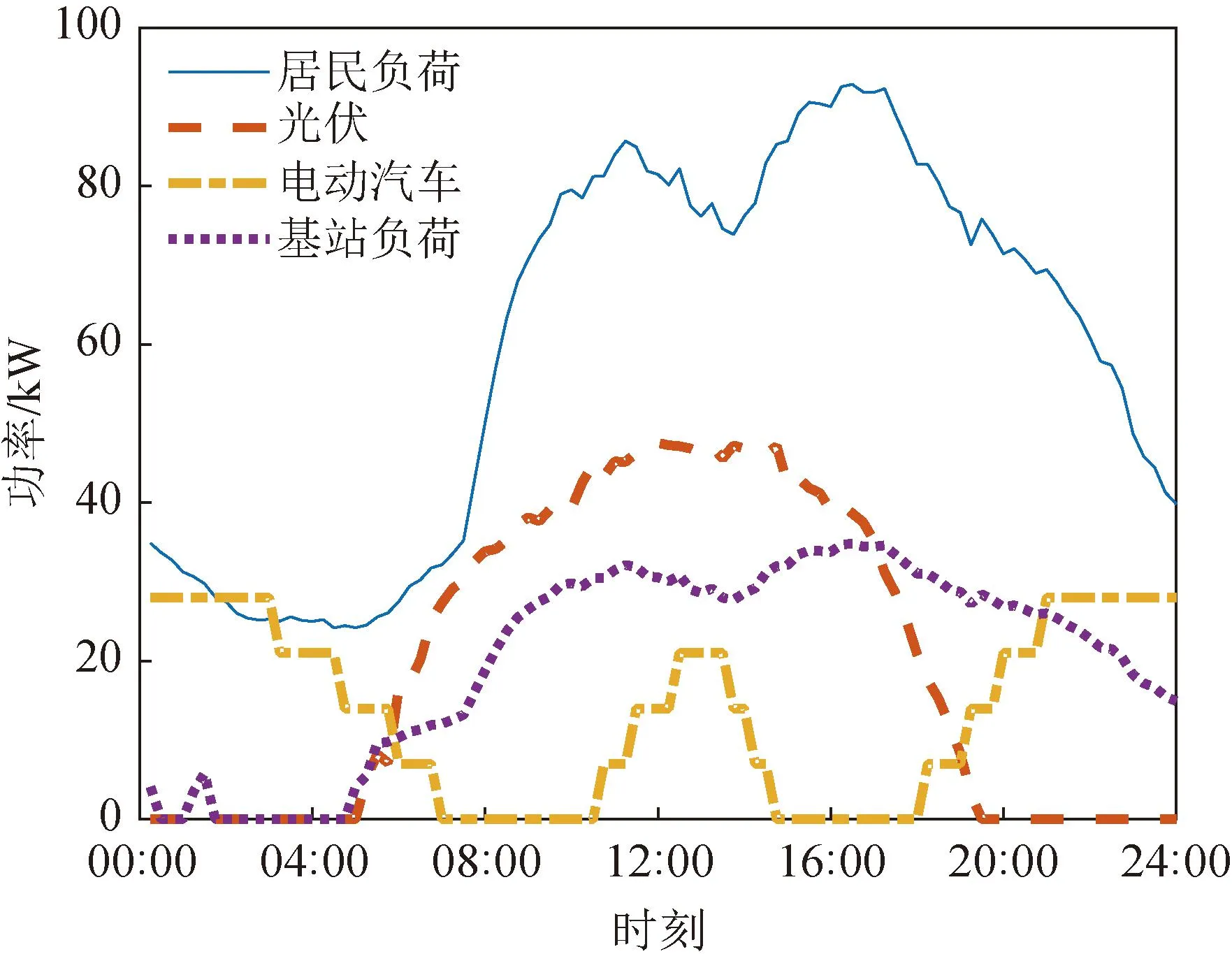
4.2 不同方案调度结果分析
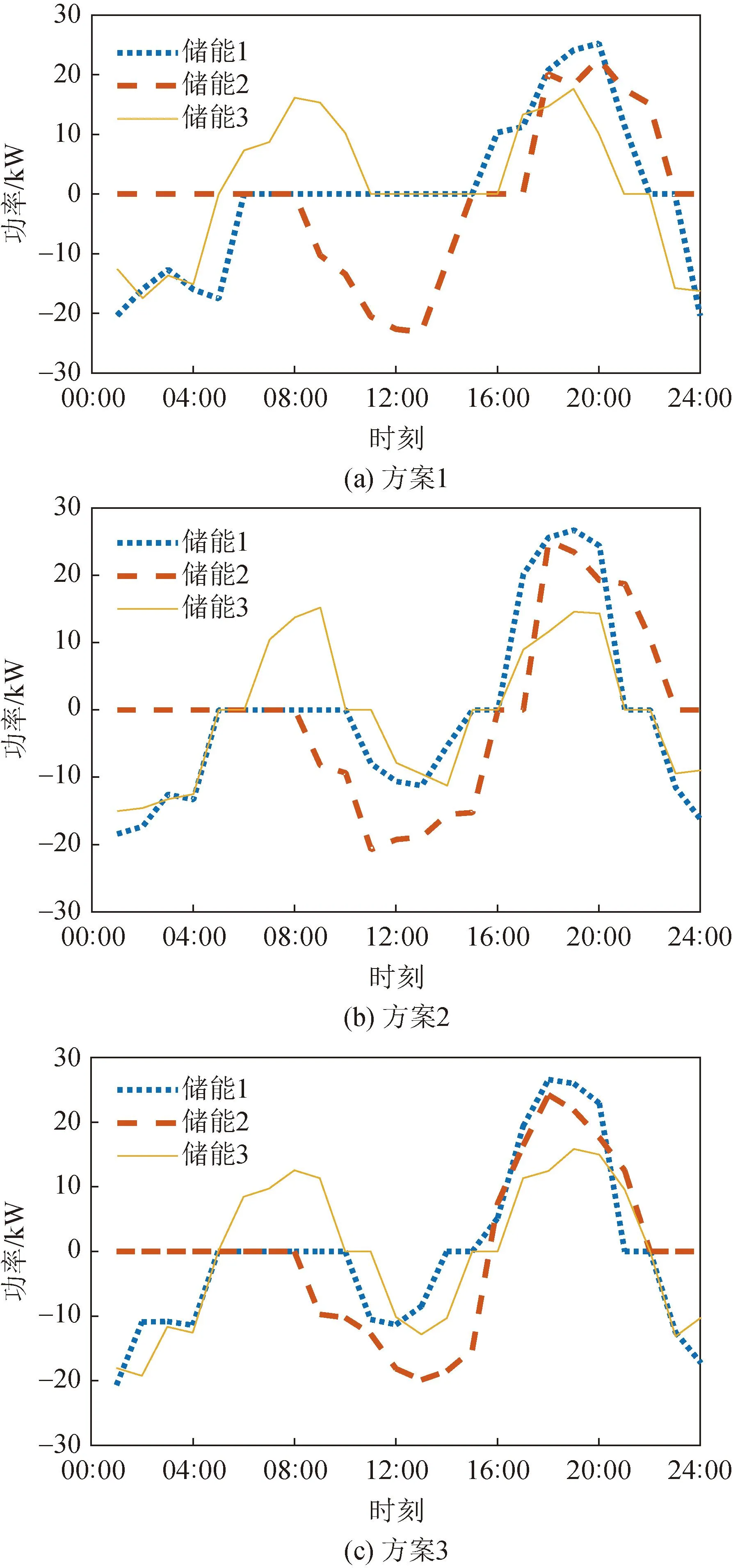


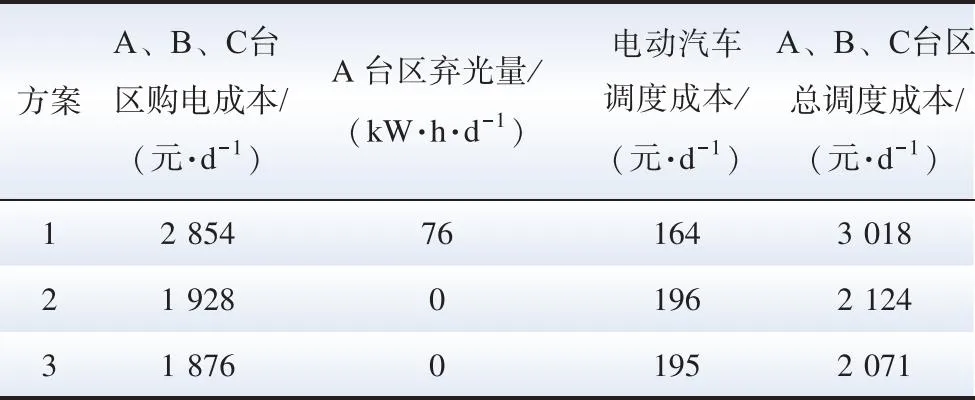
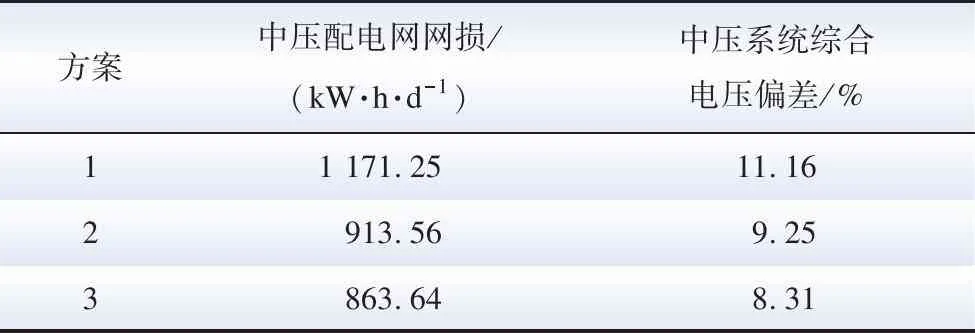

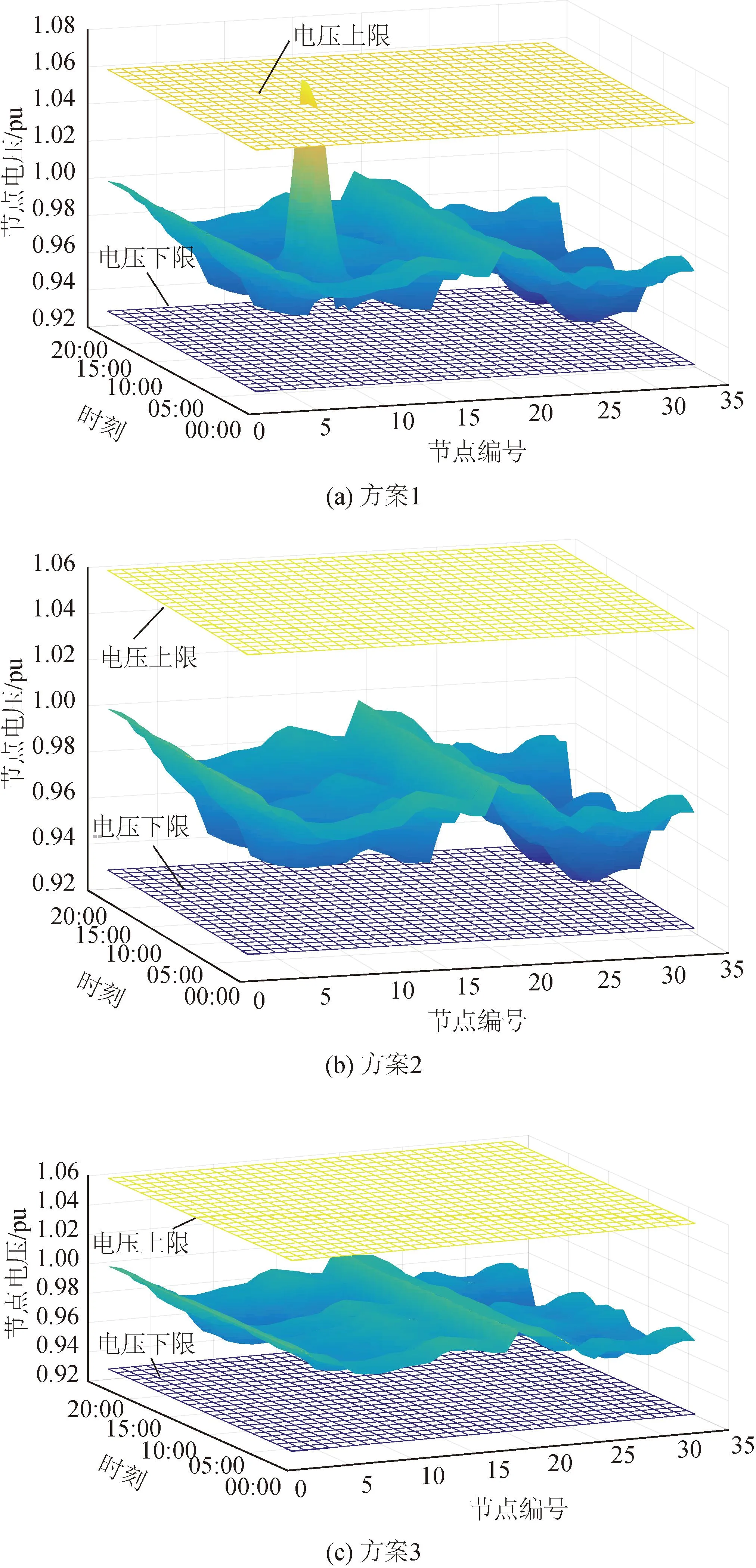
5 结 论