考虑风电时空特性和相对波动率的平衡成本分摊方法

何义琼,李鑫,贾海清,刘长玺,刘茹,谷旭东,雷霞

(1.内蒙古东部电力交易中心有限公司,呼和浩特市 010000;2.西华大学电气与电子信息学院,成都市 610039)

0 引 言

“十三五”以来,全国风电发展迅速,弃风限电情况逐年改善明显。2021年全国风电新增并网装机容量4 757 kW,同比增长16.6%;风电年发电量6 526亿kW·h,占全部电源总发电量的7.8%;年弃风电量208.8亿kW·h,弃风率下降至3.1%。“十四五”是电力低碳转型的关键期,大力发展风电依旧是主旋律,现阶段更为积极的目标应是在提升风电消纳能力的基础上,进一步完善电力交易机制和价格激励方式,促进风电和电网的可持续发展[1-2]。目前,我国现货市场建设如火如荼,其通过短时间尺度的快速交易及与中长期市场的配合,可进一步缓解风电波动对电网运行的影响并减少弃风,这也对挖掘短时间尺度的风电成本提出了更高要求。此外,风电仍以平准化度电成本为基准报价,其并网产生的成本在市场交易中未量化体现,这不利于系统对风电的接纳。只有全面厘清与现货交易时间尺度一致的风电分时段真实成本,才能保证新能源现货市场交易的公平性,并促进系统精准调度方案的制定。

风电作为清洁能源对于节能减排具有正向价值,但风力发电易受环境和自然资源影响,具有波动性和不确定性,因此,风电并网后需要常规机组或储能的启停、调节、预留备用等一系列操作来确保电力系统的实时有功平衡[3],由此带来的系统额外运行成本即为“平衡成本”[4]。针对风电平衡成本计算方法与定性分析的问题,国内外学者进行了大量的研究工作。文献[5]对大规模风电并网的美国德州电力市场进行了研究,指出在该市场环境下,风电并网会对市场其他参与者产生影响,评估风电价值不能忽视风电与其他电源之间的影响关系;文献[6]研究了英国风力发电对系统平衡成本的影响,结果表明风电并网容量增大时,系统平衡成本显著增加;文献[7]研究了风电并网时平衡成本的量化方法,基于线性回归和随机规划的方法对不同风电渗透率下的平衡成本进行了计算;文献[8]结合电力系统优化调度分析了风电波动对电网运行的影响,提出应构造无风电平衡成本的等效场景,使风电能源价值从平衡成本中剥离,在等效时将风电出力处理为恒值出力;文献[9]研究了定量分析风电平衡成本的计算思路,并分季节对不同风电接纳量系统的平衡成本进行了测算分析;文献[10]基于波形相似理论度量风电场实际出力曲线和等效出力曲线的波动整体性差异,兼顾风电场装机容量的影响,确定各风电场因未能有效跟踪负荷波动而承担的风电波动成本份额;文献[11]研究了基于平衡成本的调峰补偿成本测算方法,并在其基础上提出了风电分段调峰补偿机制,结果表明弃风段的风电因平衡成本过高而交易价值较低。以上研究工作主要针对风电在较长时间段或调度周期内总的平衡成本进行定量和定性分析,难以满足现货市场短时间尺度交易的需要,因此,有必要对风电功率短时间尺度的波动特性及其量化评估方法进行研究。

目前已有很多针对风电波动特性方面的研究。文献[12]提出一种考虑最优核函数带宽选择的改进型非参数核密度估计法,建立了风力发电随机分布模型,从不同时间尺度分析了不同区域间的风电出力概率特性差异;文献[13]提出了一种基于混合尺度参数和位置参数的t分布模型对风电功率波动变化率进行拟合,该方法基于统计原理,在对风电功率波动的研究过程中消除了时序特征;文献[14]研究了在不同装机容量和不同差分尺度下的风电功率波动特性,结果表明风电功率波动在时间尺度分布上具有趋势性;文献[15]研究了风电功率波动在不同时间、空间尺度上的分布特性,研究结果表明,随着风电场群空间分布广度的增大会使得风电功率的波动出现平缓效应,但并未对波动进行定量的刻画;文献[16]研究了不同时间分辨率下各时段风电功率波动的统计特性,实现了具有时序特征的风电功率波动特性的定量分析;文献[17]提出了分析风电功率时间序列波动性与预测误差关系的方法,对风电功率波动的时序特征进行了较为准确地描述。上述关于风电功率波动性的研究,对其功率时间序列的演进变换特征进行定量刻画的方法主要运用统计学模型,对数据要求过高,从而降低了在风电波动成本分摊中应用的实用性。

针对上述问题,本文从对风电功率波动特性的分析出发,提出一种考虑风电时空特性和相对波动率的平衡成本分摊方法。首先,构造“等电量-顺负荷”场景,考虑风电每日的出力特性,对一天的系统运行进行优化调度,对比预测场景和等效场景优化调度的系统总运行成本计算得到调度周期内总的风电平衡成本[9-10];其次,兼顾风电场的空间分布和容量对平衡成本分摊的影响,提出风电平衡成本的空间分布分摊方法。随后,提出一种用于刻画风电功率波动时序特性的指标即分时段三角系数,在此基础上进一步定义用于量化风电功率分时段波动的分时段波动率,以及反映风电相对负荷波动程度的指标即分时段相对波动率;最后,以各时段相对波动率指标为依据对风电平衡成本进行逐时段的分摊,即得到风电分时波动成本。最后以某地区含高比例风电接入的网架结构进行数值仿真分析,验证所提方法的有效性。

1 风电相对波动性及平衡成本分析

波动性是一种描述物质运动规律的物理学概念,强调的是物质的时变特性,只要事物处于持续变化的状态,就一定存在波动。据此,风电的波动性则指风电的输出功率随时间的持续变化状态。风电波动性产生的根本原因在于风机的动力元素——风能受天气和地势等多种不可抗拒的自然因素影响,且目前风电机组控制功率波动的能力有限,因此波动性是风电的固有特性。即使风电预测具有很高的准确度,甚至不存在预测误差,风电出力仍然会表现出波动性。

风电作为电源,难以像水电、火电等常规机组那样“完美”地跟踪负荷,而且其呈现的波动性及反调峰特性使得风电出力与负荷的变化趋势难以同步[18-20],因此从调度资源来看,风电既具有电源特性也具有负荷特性[21]。本文将风电与负荷的持续相对运动形式定义为风电相对波动性,将其认为是风电出力中的电源异质性,呈现的是风电的负荷同质性,是平衡成本产生的根源。

随着风电并网规模的逐步增大,风电相对波动性会对系统的运行特性造成影响[22-23]。一方面,系统净负荷的峰谷差及变化率会因风电相对负荷的波动而改变,此时,常规机组调节自身出力不仅需要实现负荷的实时匹配,还要平抑因风电并网可能导致的更大净负荷峰谷差及变化率,这势必会使得其启停等调节成本大大增加;另一方面,风电并网使系统转动惯量减少,降低了电网的耐频能力,需要预留一定的旋转备用以确保系统的安全稳定运行,使得系统预留备用容量的费用也进一步增加。因此,为了保证系统的供需平衡和安全稳定,系统需对各机组启停、出力和旋转备用等进行调节,这部分额外的系统响应成本即为风电的平衡成本。

2 风电分时段平衡成本计算

风电平衡成本的产生源于风电的相对波动性,需要由系统调度常规机组来进行平抑,因此其量化可利用电力系统运行的优化调度模型完成。求解风电分时段平衡成本的关键在于:1)将常规机组平衡风电波动的调度成本与平衡负荷波动的调度成本剥离;2)根据各风电场的容量大小及其波动特性对系统平衡成本的影响程度,将剥离出的调度成本分摊至各风电场;3)精准刻画在各调度时段风电出力相对负荷波动功率的时序演进特征,探寻风电平衡成本合理分摊至各时段的依据和方法。由于构成风电平衡成本的主体是常规火电机组,为平抑风电相对负荷波动而实施启停、调用出力及提供旋转备用而产生的成本,且各调度时段平衡成本的产生并不孤立,而是存在着必然的耦合因素,因此,计算分时段平衡成本不能简单地仅基于各时段系统局部优化调度结果进行求解,而应该先求解系统调度周期内总的平衡成本,再遵循合理原则对平衡成本进行时段分摊。

风电分时段平衡成本的计算框架如图1所示。

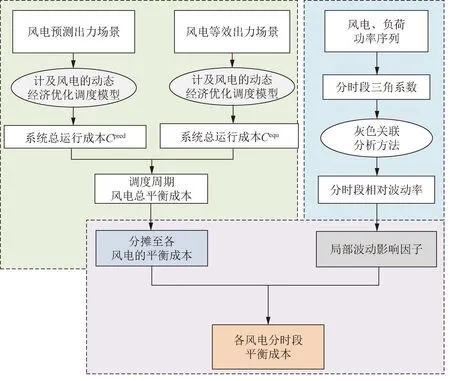
图1 风电分时段平衡成本计算框架Fig.1 The proposed calculation method flowchart of time-segment balance cost of wind power

首先对风电预测出力场景进行等效,得到零风电平衡成本的风电等效出力场景,分别计算2种场景下的系统总运行成本,二者之差即为调度周期风电总平衡成本;通过分时段三角系数对风电相对负荷波动功率序列的时序演进特征进行定量提取,基于灰色关联分析方法在一定时间窗口内(本文取15 min)筛选分时段三角系数的次优解,归一化处理后得到逐时段描述风电相对负荷局部波动程度典型状态的分时段相对波动率;以各时段风电相对负荷波动功率的局部典型状态对整个调度周期风电相对负荷功率的宏观波动特征的影响(即局部波动影响因子)大小为依据,对调度周期内风电总平衡成本逐时段分摊,即得到15 min时间尺度的风电分时段平衡成本。

2.1 调度周期风电总平衡成本计算方法

针对上述思路的关键点1,本文利用文献[9-10]提出的“等电量-顺负荷”方法构造了一个零风电平衡成本场景,将风电等效为调度周期内输出功率能够始终跟踪负荷的等效替代电源。基于系统优化调度,通过计算风电预测出力场景和风电等效出力场景下系统总运行成本差异,得到风电调度周期内的总平衡成本。

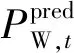
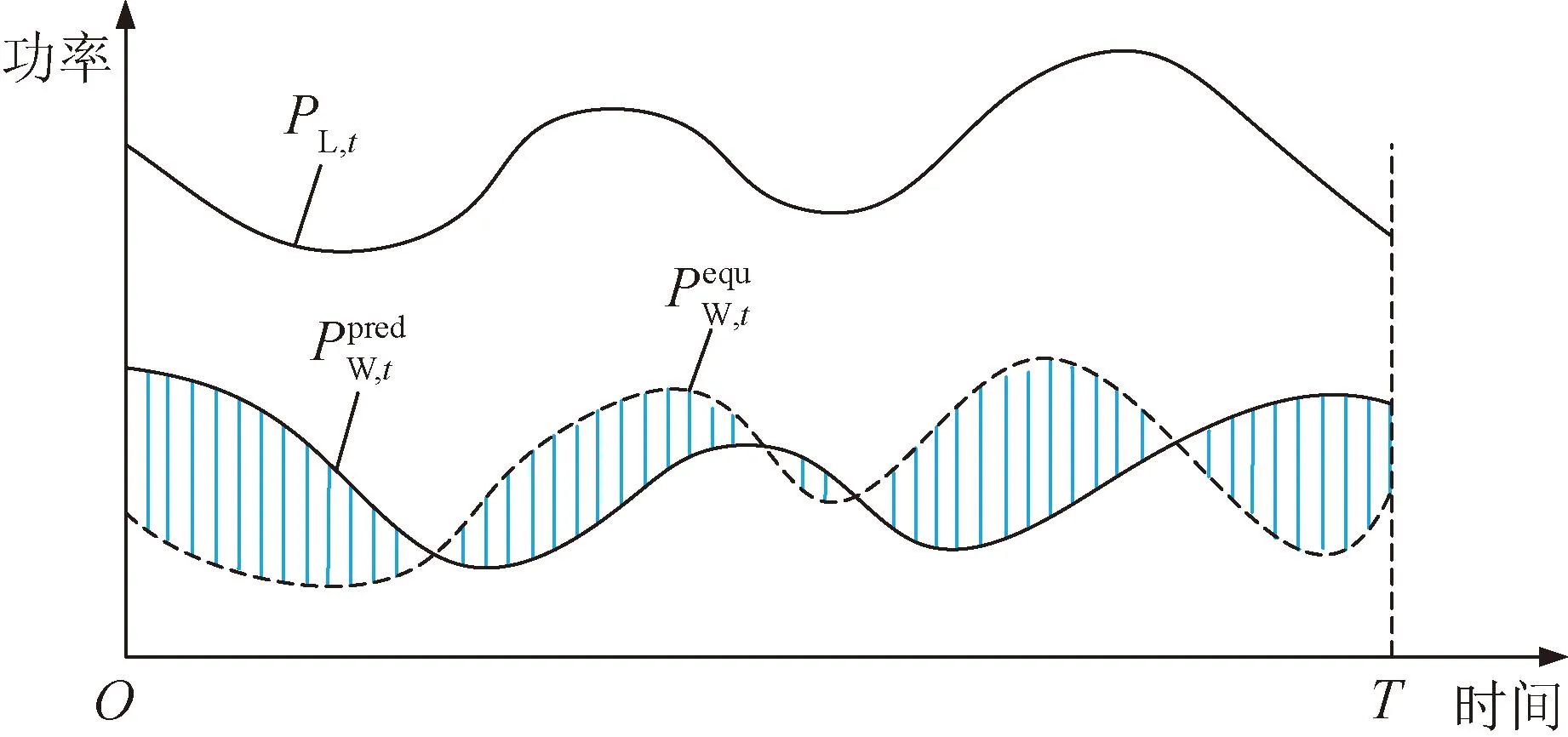
图2 风电等效替代电源构造示意Fig.2 Equivalent alternative power supply construction diagram of wind power

风电等效替代电源构造方法为:

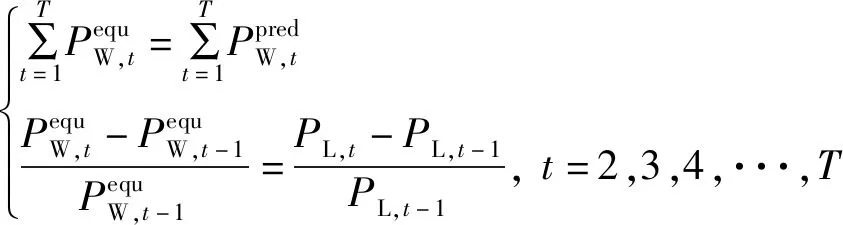
(1)

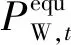
2.2 计及风电的动态经济优化调度模型

本文构建的计及风电的动态经济优化调度模型的目标是在满足负荷及系统安全运行约束的前提下同时优化火电机组出力、火电机组启停及旋转备用优化配置,使调度周期内的系统总运行成本最小。

目标函数为:

minCTOC=min(CG+CSU+CSR+CW)

(2)

式中:CTOC为系统的总运行成本;CG、CSU、CSR分别为火电机组的发电成本、启停成本、预留旋转备用成本;CW为风电运维成本。

1)火电机组发电成本。

(3)

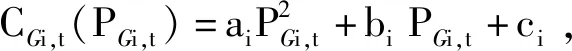
2)火电机组启停成本。

(4)

(5)

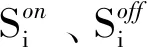
3)风电的运维成本。

(6)

式中:kW为风电场的单位运维成本;PWj,t为风电场j在t时刻的计划出力;NW为风电场数。

4)火电机组预留旋转备用的成本。

(7)

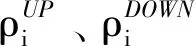
约束条件包含以下部分:

1)系统有功功率平衡约束。

(8)

式中:PL,t为t时刻总的负荷预测功率。

2)机组出力约束。

(9)

(10)

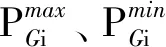
3)火电机组爬坡约束。

(11)

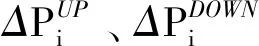
4)最小启停时间约束。

(12)

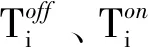
5)旋转备用约束。

(13)

(14)

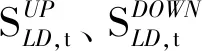
6)线路有功潮流约束。

本文中潮流约束考虑直流潮流模型,各支路有功潮流通过发电机输出功率转移分布因子矩阵Gln计算得到。

(15)

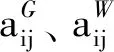
为第l条线路的有功传输上限。

将火电机组发电成本分段线性化处理后,利用上述混合整数线性规划模型分别得到调度周期内风电预测出力场景下的系统总平衡成本Cpred和风电等效出力场景下的系统总平衡成本Cequ,再由式(16)计算可得一个调度周期内风电总的平衡成本Ctot。

Ctot=Cpred-Cequ

(16)

2.3 风电平衡成本的空间分布分摊方法

实际系统中往往存在多个风电场并网,如果单独计算各自产生的平衡成本,则忽略了风电场之间的集群效应。本文综合考虑各风电场容量和对系统运行的影响大小,将总平衡成本分摊至各风电场,以解决关键点2。

风电平衡成本的空间分摊方法如下所示:

1)计算各风电场的单一平衡成本。在计算第j个风电场的单一平衡成本时,将其余风电场预测出力按前文所述等效处理,保留第j个风电场的原预测出力。计算第j个风电场原预测出力下的调度成本与风电场全部等效出力的调度成本差值,以该差值作为风电场j的单一平衡成本Cj。

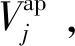
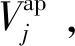
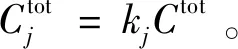
2.4 分时段相对波动率

针对关键点3,本文提出基于分时段三角系数的定量提取风电相对负荷波动功率时序演进特征的指标——分时段相对波动率。分时段三角系数与传统评估风电波动的一阶差分形式指标[24-25]侧重点各有不同。后者模型简单易懂且已经在衡量各种能量波动的研究中得到广泛的应用,其重点在于描述相邻时刻波动功率的变化;前者为了与逐时段合理分摊风电平衡成本的目标相契合,更着重于捕捉风电相对负荷波动功率序列在各时段内的持续波动特征。为了与现货交易时间尺度保持一致性,本文将风电相对波动率的时段定为15 min。

图3为风电相对负荷波动功率序列的15 min三角系数求解示意图,图中标注了个别功率极值点、非极值点、功率三角形的幅值U及相角θ。通过不同功率三角形的幅值U和相角θ可对该时段风电相对负荷功率的持续波动状态进行定量描述。

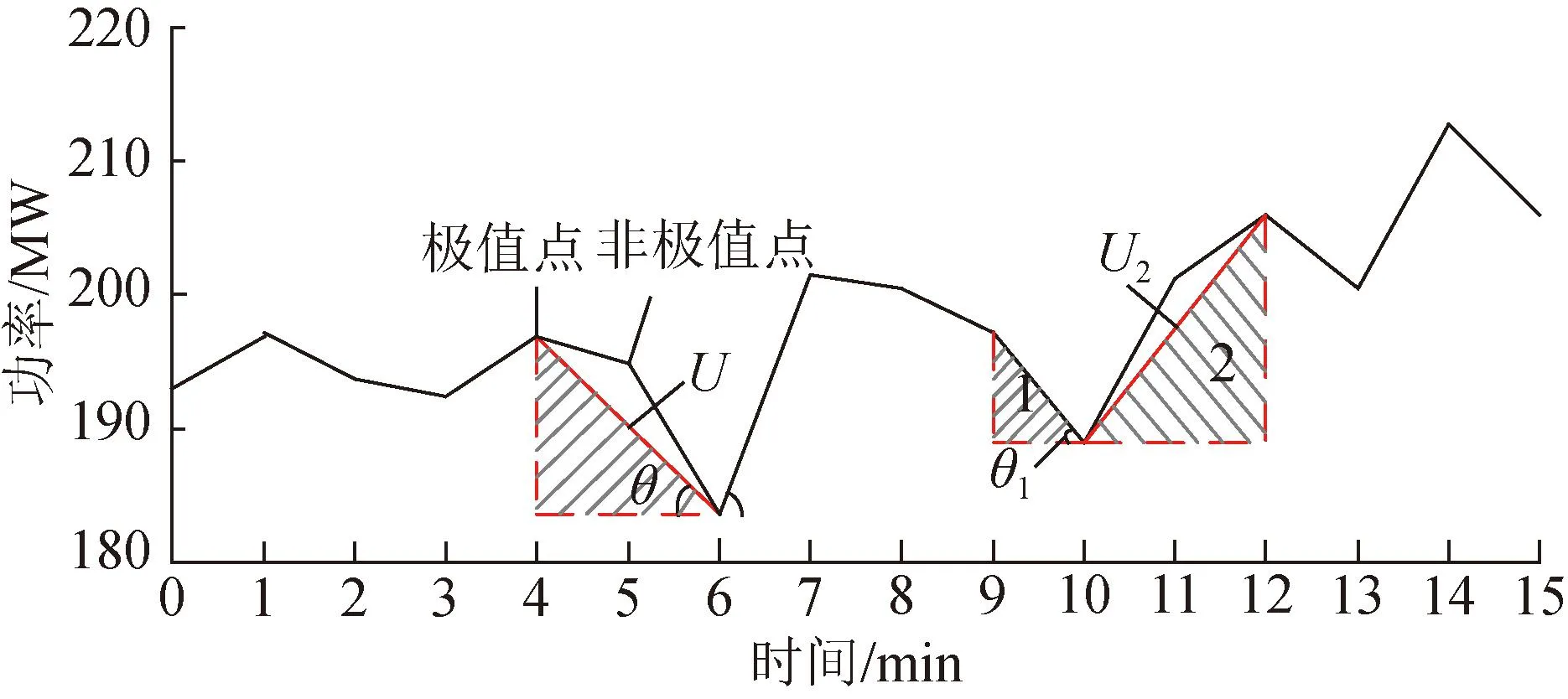
图3 功率序列分时三角系数示意图Fig.3 Diagram of time-sharing triangle coefficient of power sequence

1)逐小时输入1 min时间尺度风电相对负荷波动功率序列PW-L(1),PW-L(2),…,PW-L(k),…,PW-L(15)。

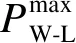
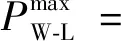
(17)

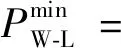
(18)

3)忽略功率序列中的非极值点,形成新的功率序列P′W-L,序列中相邻2个数据点间连线与垂直和水平方向相交后形成功率三角形,如图3中阴影部分所示。

4)计算功率序列P′W-L中各功率三角形的幅值和相角,二者共同构成分时三角系数。

在每15 min内的风电相对负荷功率序列中,如果某时段的风电相对负荷波动剧烈,则该段时间的波动功率序列变化过程应呈现变化时间快、波动幅度大的特征,即该时段的三角系数应同时满足幅值最大和相角最大2个条件。但上述2个条件难以同时满足,如图3所示,功率三角形1具有最大相角θ1,而功率三角形2具有最大幅值U2,在该时间段内,最大相角和最大幅值并未同时出现,故采用灰色关联分析法这一多属性决策方法以寻求此15 min内幅值和相角的次优解。

灰色关联决策提供了一种衡量不同因素间关联程度大小的重要量化处理方法,该方法能够找出理想最优方案对应的效果评价向量,由决策问题中各个方案的效果评价向量与最优方案效果评价向量之间的灰色关联度大小确定问题的最优解决方案和优劣排序[26-28]。通过灰色关联分析方法可挖掘代表风电相对负荷波动功率序列各时段波动程度典型状态的分时段三角系数,具体步骤如下:

1)根据事件集A={a1,a2,···,an}和对策集B={b1,b2,···,bm}构造局势集S={sij=(ai,bj)|ai∈A,bj∈B}。本文中以各时段风电相对负荷的持续波动状态为事件集A={a1,a2,···,a12},分时段三角系数的幅值和相角作为对策集B={U,θ}。

2)确定决策目标k,k=1,2,···,s。

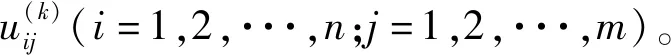
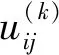
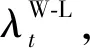
(19)

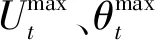
(20)

依据式(20)提取的各调度时段风电相对负荷局部波动程度特征量(即分时段相对波动率),对完整调度周期内风电相对负荷宏观波动状态的影响(即局部波动影响因子)大小,将调度周期内各风电场分摊的平衡成本逐时段进行分摊,即得到风电分时段平衡成本。

(21)

(22)

式中:Cj,t为风电场j在t时刻的风电分时段平衡成本;φj,t为风电场j在t时刻相对波动率的局部波动影响因子。

3 算例分析

3.1 算例参数概述

本文采用某地区32节点含高比例风电接入的网架结构作为计算调度周期内风电分时平衡成本进行仿真分析,系统拓扑结构如图4所示,调度时间尺度设置为15 min。

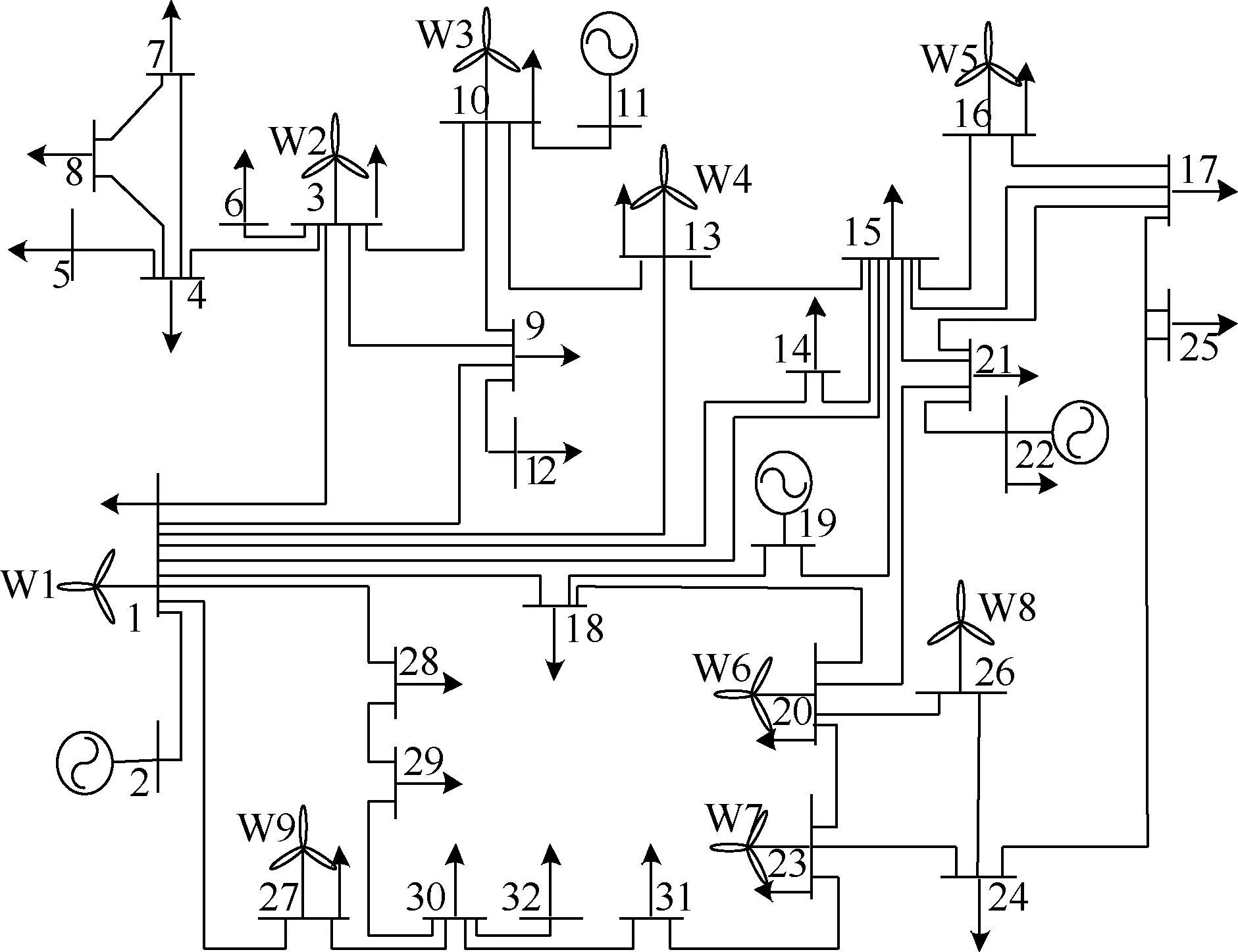
图4 某地区32节点网架结构Fig.4 32-node grid structure in a certain area

该系统包含4台火电机组,参数见表1,9个风电场,风电出力和负荷功率数据采用该地区的历史数据。其中火电装机容量为2 000 MW,占比28.6%;风电装机容量为5 000 MW,新能源发电占比71.4%。火电机组旋转备用成本为120元/(MW·h),弃风惩罚成本为160元/(MW·h)。求解各风电场出力相对于负荷的分时段波动率时,选取时间尺度为1 min的风电、负荷预测功率序列。

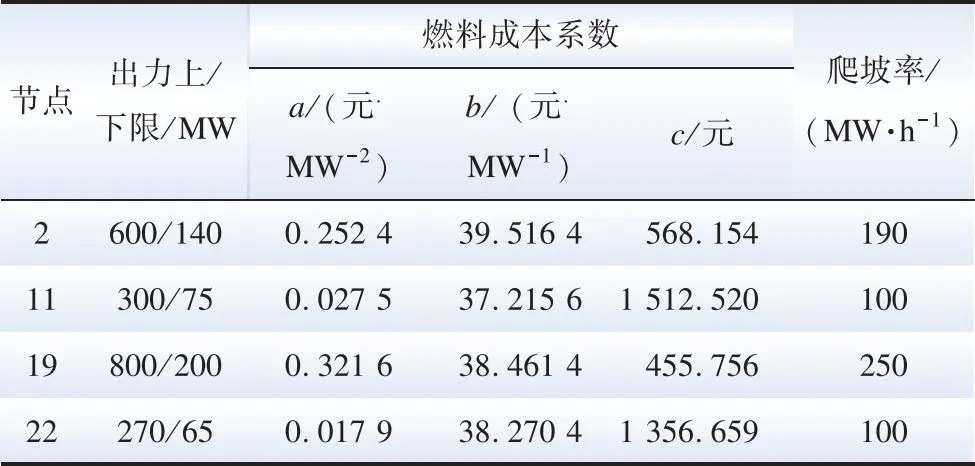
表1 火电机组运行参数Table 1 Operation parameters of thermal power units

3.2 算例结果及分析

3.2.1 风电场平衡成本分摊结果

根据本文所提风电场平衡成本分摊方法,计算出某典型日的总平衡成本为10 822.4元,其中9个风电场的分摊成本如表2所示。

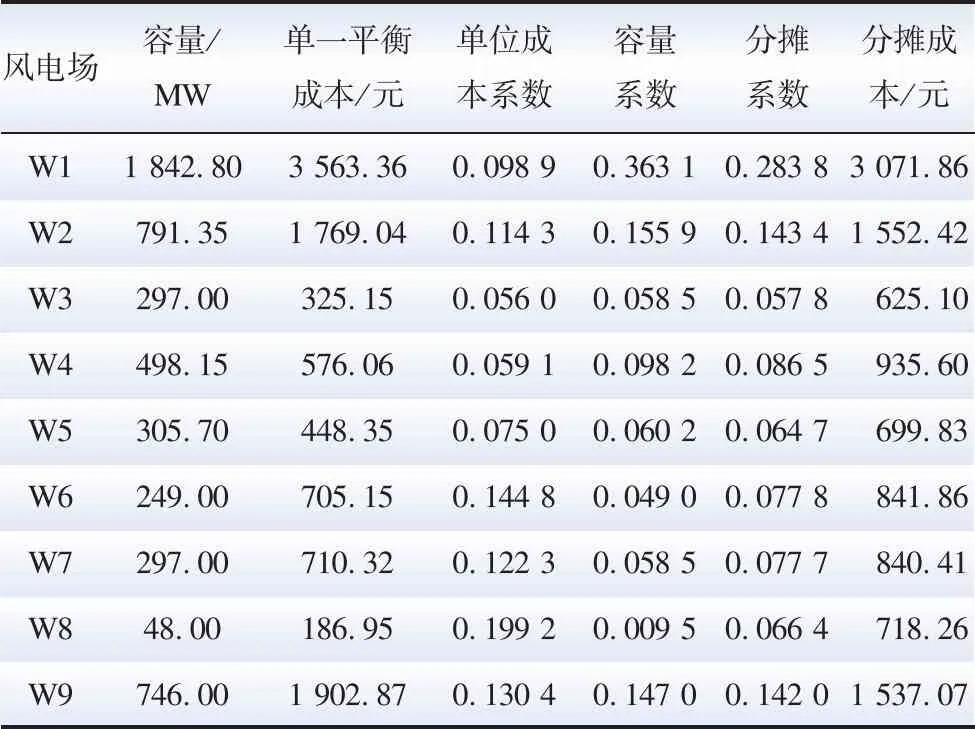
表2 风电平衡成本分摊Table 2 Balance cost allocation of wind power

表2反映了9个风电场的分摊系数及各自的分摊成本。由表2可知,W1的单位平衡成本为中等水平,但由于其容量远大于其他风电,对系统产生的影响最大,因此分摊到的平衡成本最多;W3并网下单位容量引起的平衡成本最小,且其容量也较小,因此分摊系数最小,分摊到的平衡成本最少;W8虽然容量最小,但由于其波动特性对系统安全运行影响较大,所以其分摊的平衡成本比较大。

3.2.2 风电的空间分布对平衡成本分摊的影响分析

为分析风电的空间分布对平衡成本分摊的影响,本文将W7、W8的容量相易,同时不改变其出力预测曲线的波动趋势,再根据本文所提风电场平衡成本分摊方法重新进行计算,计算得到某典型日的总平衡成本为11 351.70元。各风电场的分摊成本如表3所示。

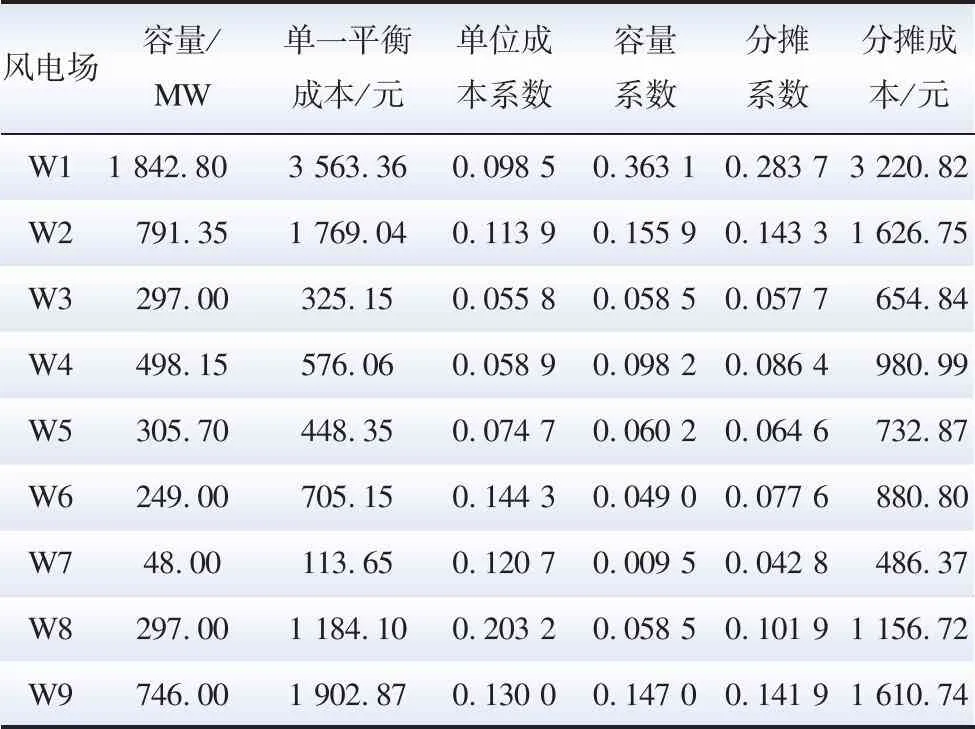
表3 W6、W7容量相易后风电平衡成本分摊Table 3 Balance cost allocation of wind power after capacity conversion of W6 and W7

在W7和W8容量相易,出力预测曲线波动趋势不变的情况下,系统的总平衡成本是略微有所增加的,对比表2和表3中W7和W8的单位成本系数可知,系统总平衡成本的增加是由于相对负荷波动程度更大的W8的容量增大引起的。对比表2和表3中W7和W8的分摊成本可知,在机组容量变化、出力预测曲线波动趋势不变的情况下,各机组的并网容量发生改变会影响其分摊到的平衡成本。对比表3中容量相同的W3和W8机组可知,在容量相同的情况下,风电场的单位成本系数更高,则其分摊到的平衡成本更大。这说明风电场相对负荷波动程度的大小会影响到平衡成本的分摊。

由以上结果分析,风电场在系统中所处的空间位置将会影响其并网产生的平衡成本,这是由于风电场所处的地理位置不同,其风力资源也不同,进而导致其风电的出力特性不同。同时,在同一地理位置,若风电场的容量增大,则其对系统的影响也将增大。本文所提风电平衡成本的空间分布分摊方法在进行系统总平衡成本分摊时,同时考虑了风电场容量及其相对负荷波动程度对系统总平衡成本分摊的影响。

3.2.3 风电波动程度对分时段平衡成本的影响分析

为分析风电出力波动程度对分时段平衡成本的影响,本文选取表2中容量相近且分摊成本基本相同的风电场W6、W7进行分析。图5为W6、W7的净负荷曲线以及其分时段平衡成本。通过对比分析不同风电波动程度下风电分时段平衡成本的差异和变化来确定其影响关系。

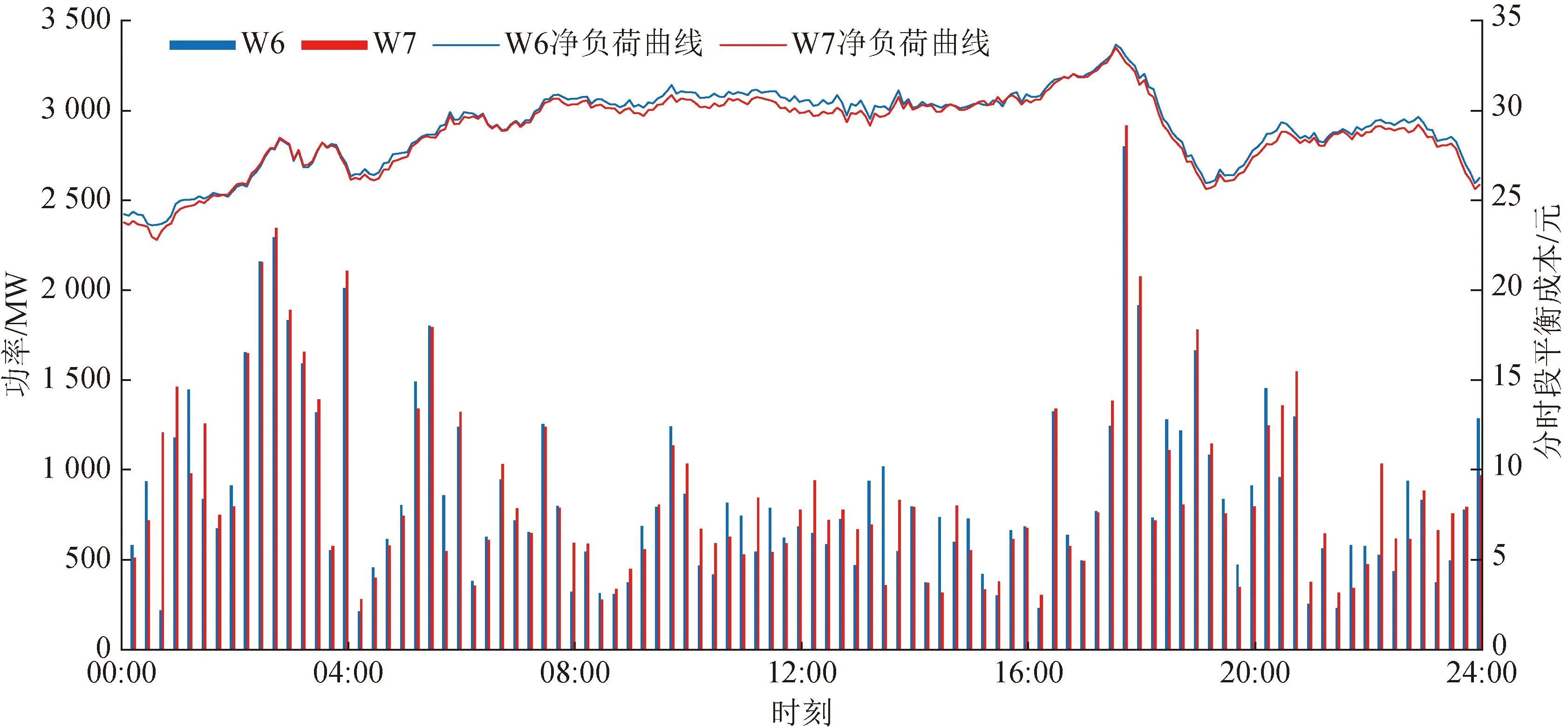
图5 W6、W7净负荷曲线及分时段平衡成本对比Fig.5 Comparison of net load curves and time-segment balance costs of W6 and W7

结合图5可知,各时段的平衡成本大小与风电场的净负荷曲线的波动程度呈正相关,风电场净负荷曲线的波动程度体现了风电场追踪负荷的能力。在净负荷曲线波动较剧烈的时候,表明风电追踪负荷的能力较差,该时段的平衡成本就较高,如图5中17:00—20:00所示。反之,净负荷曲线波动较平稳的时候,表明风电追踪负荷的能力较好,该时段的平衡成本较低,如图5中08:00—16:00所示。在图5中,W6、W7的净负荷曲线整体趋势大体相近,但各个时段内的波动率存在差别,这也导致了两者在各个时段内的分时段平衡成本有所差异。本文所提的分时段相对波动率为风电总平衡成本进行逐时段分摊提供了量化依据。

4 结 论

为解决新能源现货市场的定价问题,针对风电接入电网后其固有的波动性给常规机组带来的额外调节成本,本文结合日前优化调度模型,研究了一种基于风电相对负荷波动功率特性分析的风电分时段平衡成本计算方法。提出了定量描述风电相对负荷波动功率序列时序演进特征的指标即相对波动率,并基于相对波动率获取局部波动影响因子对风电调度周期总平衡成本进行了逐时段分摊,通过算例仿真验证了模型的有效性,得到不同风电并网容量、不同风电波动程度下的分时段平衡成本计算结果。从算例结果可以看出,风电并网容量越大,其对系统平衡成本产生的影响也就越大;风电在某时段内相对于负荷波动越剧烈,则在该时段对应的平衡成本也越高。且风电的平衡成本是一个动态值,会随着风电功率、负荷需求的实时波动及系统灵活调节能力的改变而持续变化。本文所提的风电分时段平衡成本计算方法,一是对风电场在某地理位置的容量规划有一定的指导意义;二是对后续建立健全现货市场风电交易机制和价格激励方式具有一定的实际价值,亦可为风电消纳的辅助服务市场价值研究提供理论分析基础。