直流网光伏系统多时间尺度调度算法

叶清泉,倪佳华,吴旭光,陈伟,吴明启,项基

(1.国网浙江省电力有限公司平阳县供电公司,浙江省温州市 325400;2.浙江大学电气工程学院,杭州市 310015;3.平阳县昌泰电力实业有限公司,浙江省温州市 325400;4.浙江大学工程师学院,杭州市 310027)

0 引 言

电网调度历来是电网运营的重要组成部分,科学的调度能降低电网运营成本、改善电能质量,提升经济效益[1-4]。光伏低渗透率情况下,光伏一般以最大功率模式运行,电网调度延续传统的模式,通过调度储能和燃料发电机来消纳光伏的不确定性波动并优化运营成本[5-7]。

随着光伏渗透率的增加,电网消纳光伏波动的成本也随之增长,光伏的最大功率运行模式已难以为继,电网调度开始将光伏作为一种容量可变的电源纳入调度范畴[8-10]。文献[11]建立了包含多种电源类型的混合动态经济排放调度优化模型,并通过增强的蛾火优化算法求解。文献[12]提出了光伏启停和出力优化的混合整数非线性模型,利用正则化和半正定松弛技术将该模型松弛为凸优化问题后求解最优值。文献[13]提出了一种多能合作博弈优化模型,采用均衡度对比各主体收益,通过智能优化算法求解最优调度量,以求达到各主体的收益分配公平性。文献[14]提出了负荷跟踪、功率平滑两种出力模式的调度模型,利用非支配排序遗传算法和层次分析法确定最优调度方案。但是,这些文献都是以预测后得到的光伏容量为基础,从潮流优化或能量平衡的角度利用不同工具求解光伏等新能源接入下的多目标最优问题,没有考虑光伏出力的不确定性。

为了减小光伏不确定性波动带来的影响,提升电网电能质量,学者们研究如何把光伏不确定性纳入调度考量。文献[15]提出了基于机会约束的电网动态经济调度模型,将光伏的出力预测误差用随机变量表示,把机会约束转化为确定性等价类,最后用改进的粒子群优化算法求解。文献[16]提出了基于电源分类的两步式优化调度,首先用三阶混合高斯分布量化光伏可用容量预测误差,用蒙特卡洛法估计光伏不确定性的成本函数期望值和方差;然后用粒子群优化算法在一定量的样本中找到成本均值最优的调度方案。文献[17]提出了一种基于区间线性随机机会约束规划的优化调度策略,以正态分布函数量化光伏预测误差,得到机会约束规划模型,再用常规的规划方法求解。文献[18]提出了一种基于模型预测控制的优化调度方法,以光伏出力作为扰动变量,柴油机和储能作为控制变量,基于未来一段时间已知的扰动变量进行滚动优化和反馈矫正,以保证调度结果的鲁棒和抗扰性。文献[19]提出了一种多目标鲁棒优化调度方案,对光伏的不确定性做区间估计代入鲁棒优化模型,以兼顾系统的灵活性和稳定性。这些文献都从数学角度对光伏出力的不确定性进行了量化建模,以此刻画出力不确定性对整体调度的影响。但是,这些文献都提前对光伏不确定性波动做出了调整,以减小未来发生光伏波动时的影响。此类方法牺牲了当前时刻下的最优调度性能以弥补未来的不确定性影响,并且无法实时响应光伏的功率偏差。

有学者通过对模型或算法的训练,使光伏系统输出自适应光伏的不确定性波动。文献[8]定义了一个参与因子用以刻画调度周期间光伏对指令的跟随程度,以此动态调整下一个周期的参与度,减少不确定性带来的影响。文献[20]提出了一种基于神经网络的调度方案,利用历史数据训练神经网络以提取光伏不确定性特征,在调度中依据预测的波动特性进行提前响应而增强系统稳定性和经济性。文献[21]提出了一种基于自适应约束随机模型预测控制的调度策略,光伏的不确定性可以根据违规水平与期望水平的实际偏差概率以及偏差概率的当前变化率自适应地收紧或放松约束。文献[22]提出了一种基于深度强化学习的自适应不确定性调度方法,引入深度强化学习中深度确定性策略梯度算法,通过训练完成的模型自适应光伏随机波动,避免了对复杂不确定性的建模。然而,光伏出力的随机性特征是难以用数学模型精确量化和提取的,所以上述方法在实际使用过程中对光伏功率偏差的应对效果是无法保证的。

综上,光伏系统经济调度的相关研究中,已有调度方法没有实时精确处理光伏不确定性带来的功率缺额问题。当前研究对调度中光伏不确定性的处理方法主要分为两类:量化和特征化。量化,就是用经典概率函数或可缩放的扰动变量描述光伏不确定性输出功率,以此得到带随机变量的潮流优化模型,然后利用各种求解工具求解。特征化,就是对历史光伏波动特征进行学习和提取,在算法运行中可以动态地自适应调整光伏的调度,避免了对复杂不确定性的建模。当前在调度中对光伏不确定性的处理思路是通过对不确定性的预估,提前预留一定的备用功率,以此减少不确定性波动发生时的负面影响。但是,光伏的随机性和间断性是难以被准确量化和度量的,所以在调度间隙还是会发生光伏缺电现象,由此恶化电能质量。虽然提高调度频率可以缩短调度间隔,以实现对光伏更及时的调度,但是这无疑会增加调度中心的计算负担,尤其在大规模电网中,调度周期还会受信息传输和处理速度的制约。因此,当前的研究空白在于缺乏一种低负担的方式直接实时响应光伏的调度功率偏差问题。

本文提出了一种多时间尺度的光伏系统调度策略,以实现光伏热备用的经济高效调度。不同于传统的在集中式调度算法对光伏的不确定性进行数学建模,所提调度方法引入了一致性分布式调度配合集中式调度方法。所提调度算法在不同时间尺度整合了集中式调度和分布式调度算法的优势:在长时间下的集中式调度算法,可以根据全局信息实现全局优化;在短时间尺度下的分布式调度算法,可以根据光伏电源相邻节点间的信息实时调度备用功率。所提调度算法无需对光伏输出的不确定性进行复杂建模,可以实时响应光伏不确定性波动带来的功率输出偏差,又保证了全局最优调度。

本文将首先分析光伏在不同天气条件下的出力特征,再对传统集中式调度方法及其存在问题进行阐述,然后介绍本文所提的多时间尺度调度方法,最后在IEEE 5节点和IEEE 14节点系统上测试所提算法的性能。

1 光伏在不同天气条件下的出力特征

光伏出力受到环境的影响(辐照度、温度等),具有随机性和不确定性。如图1所示,分别为额定容量1 kW的光伏面板在杭州晴朗和多云天气下的最大出力变化曲线。在晴朗天气下,如图1 (a)所示,光伏出力相对稳定,其可用容量呈现钟型分布。图1 (b)在20 min内展示其可用容量,光伏容量变化很小,波动在10 W以内。在多云天气下,如图1 (c)所示,阳光受不确定性云朵影响,其光照强度存在随机波动,导致24 h内的光伏可用容量曲线也存在随机和不确定性波动。图1 (d)同样为20 min内的容量变化曲线,其在20 min内的可用容量波动高达220 W。

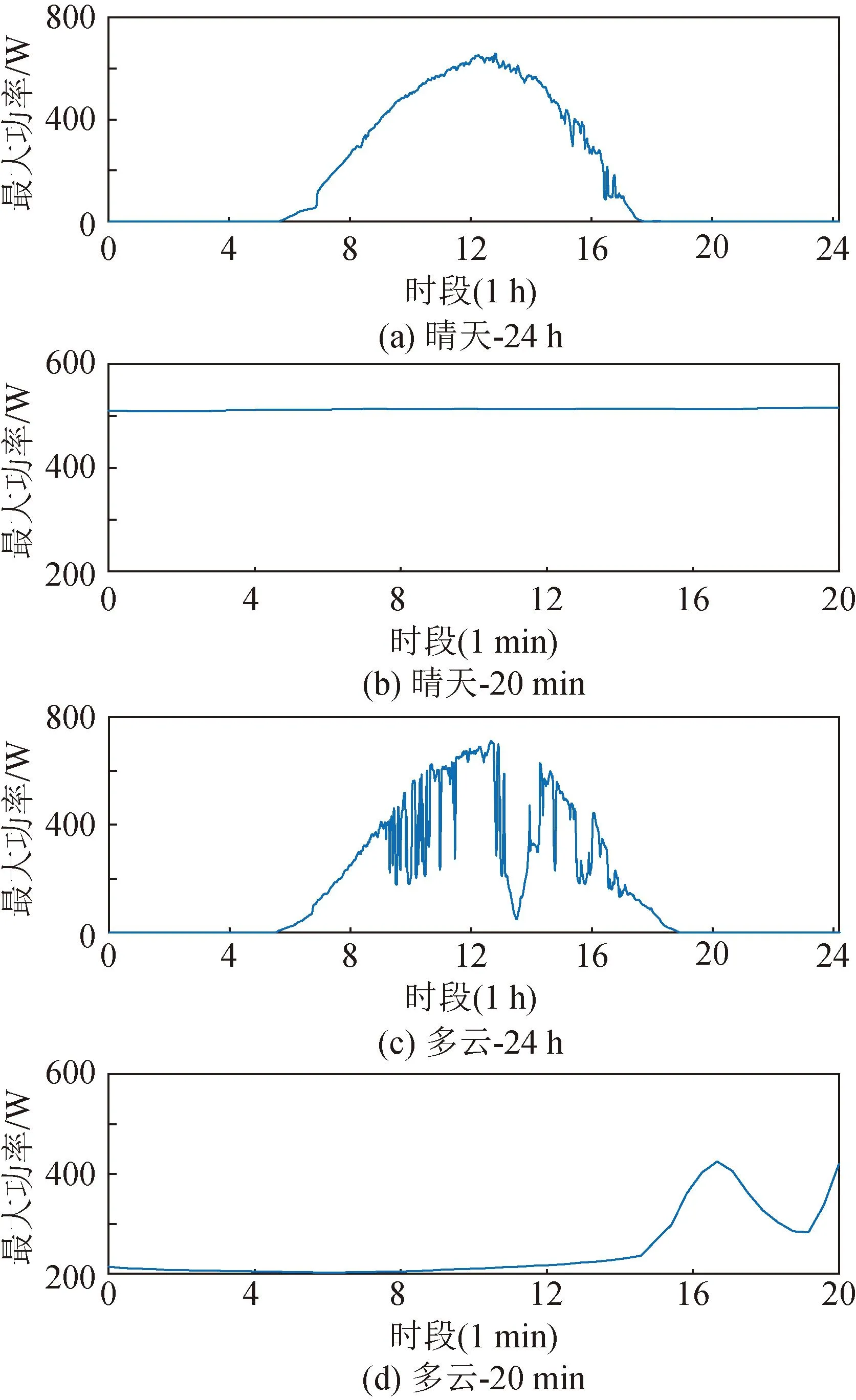
图1 同一光伏面板在不同天气情况下的出力Fig.1 A PV panel’s maximum power under different weather condition

2 传统调度算法及其存在问题

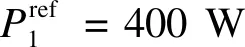
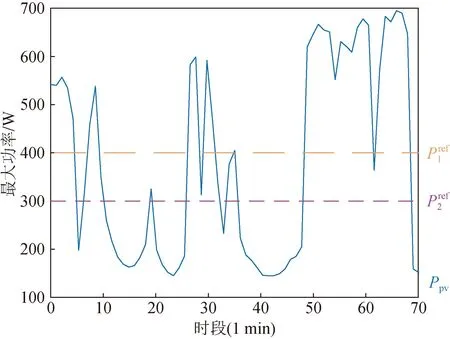
图2 不同功率输出参考值下的交互曲线Fig.2 The interaction curves with different power references

2.1 传统调度算法

在传统发电机为主体的配电网中,为了使得运行成本最小,其调度优化目标一般为发电成本最小:

(1)

式中:Pg是发电机输出有功功率矩阵;G为发电机集合;Pg,i为第i台发电机的输出有功功率;c2,i,c1,i,c0,i为发电成本系数。

或者网损最小:

(2)

式中:I是支路电流矩阵;L为支路集合;Imn为支路mn上的电流值;Rmn为支路mn的等效阻抗。

从上面两式可知,传统的调度算法本质上是在满足负荷需求的前提下,尽可能减少发电机的燃料消耗成本和线路损耗。但是,当电源由光伏系统构成时,情况有所不同。光伏,作为一种新能源电源,其安装完成后,发电成本是忽略不计的。而且,从发电用户侧考虑,总是希望其发得越多越好,以提升售电收益,所以光伏的调度会从其热备成本和节点电压偏移角度考虑,调度优化目标为:

minf=cψΨ(I)+cφΦ(Pc)+cγY(V)

(3)

式中:cψ≥0,cφ≥0,cγ≥0为权重系数;Ψ(I) 为线损函数;Φ(Pc) 为光伏备用功率函数;Y(V) 为节点电压相关函数,三者的具体表达式如下:

1)线损函数:网络中的功率损耗。

(4)

2)功率热备函数:光伏功率热备带来的成本。

(5)

式中:H为光伏集合;ah,bh为成本系数;Pc,h为第h台光伏电源的备用功率。

3)电压偏移函数:各节点电压偏移平均值的程度。

(6)

式中:N为节点集合;n为节点个数;Vi为节点i的电压。

2.2 问题描述

对比式(2)和式(3)可知,后者增加了备用功率成本和电压偏移代价函数,但是仍然存在两个问题:其一,网损最小和热备成本最小的目标是矛盾的,在负荷一定的情况下,备用功率等于可用容量减去负荷,要减小备用功率,唯一的途径就是增加网损,显然对于电网运营方,即购电方,是不能接受的;其二,调度指令往往是基于当前时刻光伏的可用功率,在调度指令更新的时间间隔内,光伏的可用容量是会随着环境变化而发生不确定波动的,光伏出力的优化没能考虑实际可用容量不确定变化带来的影响。如图3 (a)所示,红色为调度指令,每10 min根据当前光伏的可用功率更新一次,但是受光伏出力不确定性的影响,在下一次调度指令更新之前,可用功率可能小于调度指令,如阴影部分所示。有一种自然的方案就是缩短调度指令更新间隔,如图3 (b)所示,当调度指令更新时间间隔从10 min缩短到5 min,在同样的光照条件下,光伏系统发生功率偏差的时间有所减少,但是越高的调度指令更新频率,意味着越多的数据传输和处理量,尤其是在节点众多的大规模网络中,对于中央处理器是一个不小的负担。

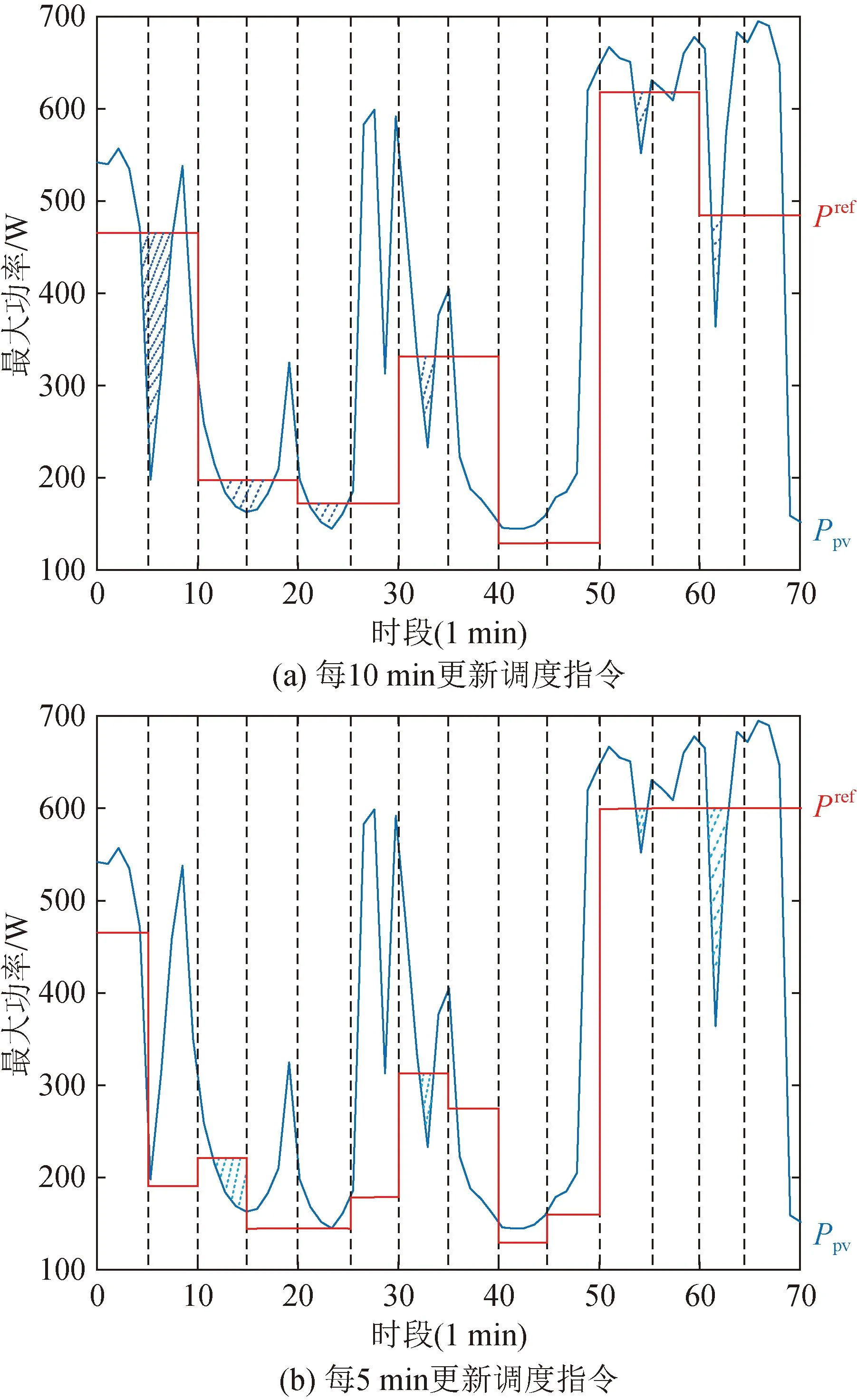
图3 调度指令下的交互曲线Fig.3 The interaction curves with different dispatching orders

3 所提调度算法

为了解决集中式调度算法更新频率和计算负担之间的矛盾,本文提出了多时间尺度的调度方案:上层是集中式的潮流优化调度方法,以满足网损和节点电压要求;下层是分布式光伏热备调度方法,以解决光伏调度功率偏差问题。两者执行的频次和信息交互方式如图4所示,图4(a)中红色方块为集中式调度执行时间,蓝色方块为分布式调度执行时间,由图可见,分布式调度的时间间隔更短其执行频率更高;图4(b)中红色虚线为集中式调度的信号传输线,蓝色实线为分布式调度的信号传输线。因为集中式调度收集各节点的负荷和容量信息,结合网络拓扑进行全局优化,因数据量一般较大,指令更新间隔较长频率较低,而分布式调度算法只运行在各节点本地,和相邻节点进行信息交换,指令更新间隔较短频率较高。

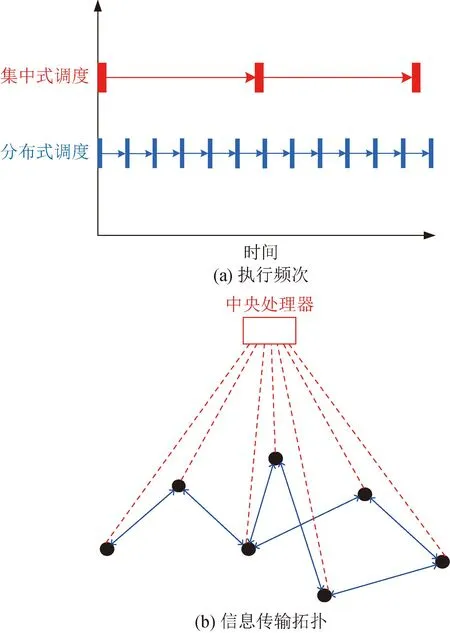
图4 集中式和分布式调度逻辑Fig.4 Logic of center dispatching and distribute dispatching

3.1 上层集中式调度算法

本文从电网运营者的角度调度光伏输出功率,所以无需考虑光伏热备成本,上层调度优化算法以网损最小和电压偏移最小为目标,其目标函数如下:

(7)

式中:V为节点电压矩阵。

根据图5所示的支路模型,可建立如下约束:

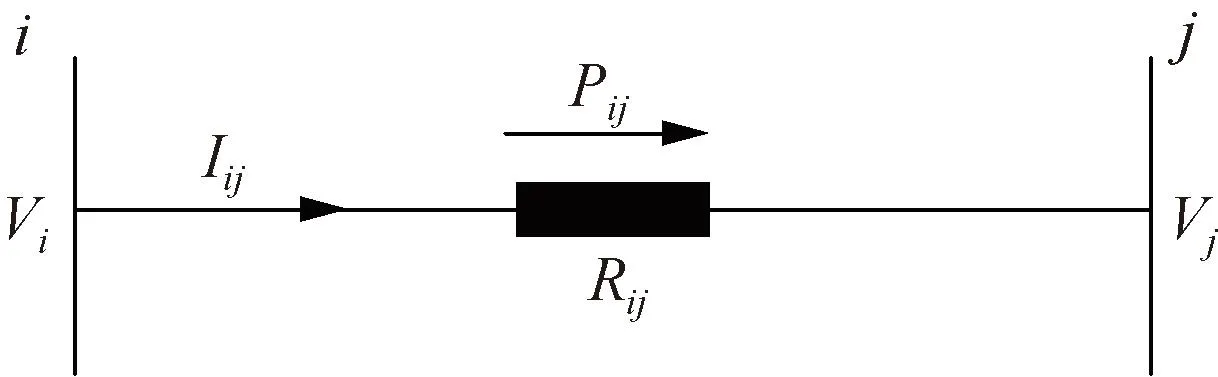
图5 支路模型Fig.5 Branch model

1)功率平衡约束。

(8)

(9)

(10)

式中:Pg,i是i节点处光伏电源的输出功率;Pd,i是i节点处负荷的功率;E+={(i,j)|ij且i,j∈N}为有向支路集,(i,j)表示两点节点为i,j且正方向为i→j的有向支路;E+为功率流出i节点的支路集合;E-为功率流入i节点的支路集合;Pij为节点i流向节点j的功率。

2)节点电压约束。

(11)

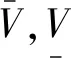
3)光伏约束功率。

(12)

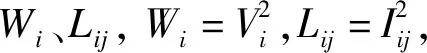
(13)

(14)

电压约束式(11)变为:

(15)

4)二阶锥松弛。

式(14)可以松弛为如下:

(16)

式(16)为二阶锥松弛约束,等价于如下约束:

(17)

式(17)可以表示为如下二阶锥松弛标准格式:

(18)

5)凸优化模型。

综上,可以得到如下凸优化模型:

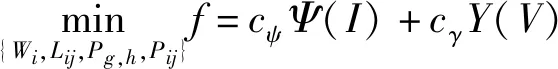
(19)

3.2 下层分布式调度

分布式调度算法的目的是调度光伏备用功率,让留有多余备用功率的光伏电源根据一定规则调整输出功率,以补足部分光伏电源因受光照影响而产生的功率偏差。分布式调度算法的指令更新频率可以在集中式优化调度的10倍以上,各节点只和相邻节点交换数据,因此无需担心计算负担,且适应拓扑多变情况。

1)算法描述。

光伏电源间构成强连通的无向图G=(N,E),节点个数为n,节点集合N={1,2…,n},边的集合为E,各节点的度为D={d1,d2…,dn}。Ps,i为节点i处的光伏电源功率偏差,指可用容量不足时,输出参考功率和可用容量之间的功率差额,即Ps,i=Pref,i-Pmax,i,Pref,i>Pmax,i,容量充足时,功率偏差为零,即Ps,i=0,Pref,i≤Pmax,i;Ps={Ps,1,Ps,2…,Ps,n}为各电源功率偏差构成的向量;Ps(k)为k时刻的功率偏差向量;每两个时刻的间隔时长为分布式算法执行的周期。

分布式一致性平均算法可表示为:

(20)

式中:P′s(k+1)为中间变量;A=[aij]n×n为权重矩阵;f(·)为自定义运算。

权重矩阵A设计为Metropolis-Hastings矩阵[26],即:

(21)

由于当功率偏差被分配到有多余功率热备的光伏节点时,功率偏差会被节点消纳,此时偏差置零,所以需要对平均后的功率偏差进行处理,运算规则f(·)为:

(22)

即,当前电源输出功率增加分摊的功率偏差后[Ps,i′(k+1)+Pref,i(k)],若超过可用容量[Ps,i′(k+1)+Pref,i(k)>Pmax,i(k)],则超出部分为其功率偏差,如未超过[Ps,i′(k+1)+Pref,i(k)≤Pmax,i(k)],则分配的功率偏差被全部消纳,其功率偏差为零。

2)稳态分析。

上文所提出的分布式一致性平均算法和经典的分布式一致性平均算法有所不同,即每一次运算后会经过f(·)运算调整。但是,其稳态值可以根据经典分布式一致性平均算法的理论推导得到。

首先,回顾经典分布式一致性平均算法的运算规则和稳态值。假设每一次运算结果不经过f(·)函数调整,则可以得到经典分布式一致性平均算法的表达式:

Ps(k+1) =A·Ps(k)

(23)

因为权重矩阵A是双随机的(1nA= 1nandAT1n= 1n),根据Perron-Frobenius 原理[26],可得到经典分布式一致性平均算法的稳态值:

(24)

式中:1n为元素全为1的n维向量。

然后,分析所提分布式一致性算法的稳态情况。因为在平均分配过程中,有多余热备的光伏电源会消纳部分功率偏差,所以总的功率偏差是随时间非增的,即:

(25)

根据光伏可用功率和输出参考功率之间的关系可得以下两种情形:

情形1：总的光伏可用功率小于等于总的参考功率之和那么必然在某一个时刻k1,光伏可用热备均被消耗完毕,此时:

Pref,i(k)=Pmax,i(k),∀i∈N且k≥k1

(26)

结合式(20)、(22)和(24),可得:

(27)

情形2：总的光伏可用功率大于总的参考功率之和,那么必然在某个时刻k2,功率缺额被全部消纳,此时:

Ps,i(k)=0,∀i∈N且k≥k2

(28)

同理可得:

(29)

式中:On是元素均为0的n维向量。

3)算法实现。

上文已经对分布式一致性算法进行了数学描述,为了指导部署和实施,现给出各节点结合集中式调度指令的实现伪代码,如图6所示。每一个分布式算法调度周期下,各节点都根据自身的备用功率和周围节点的功率偏差功率信息更新调度指令Pref,i。

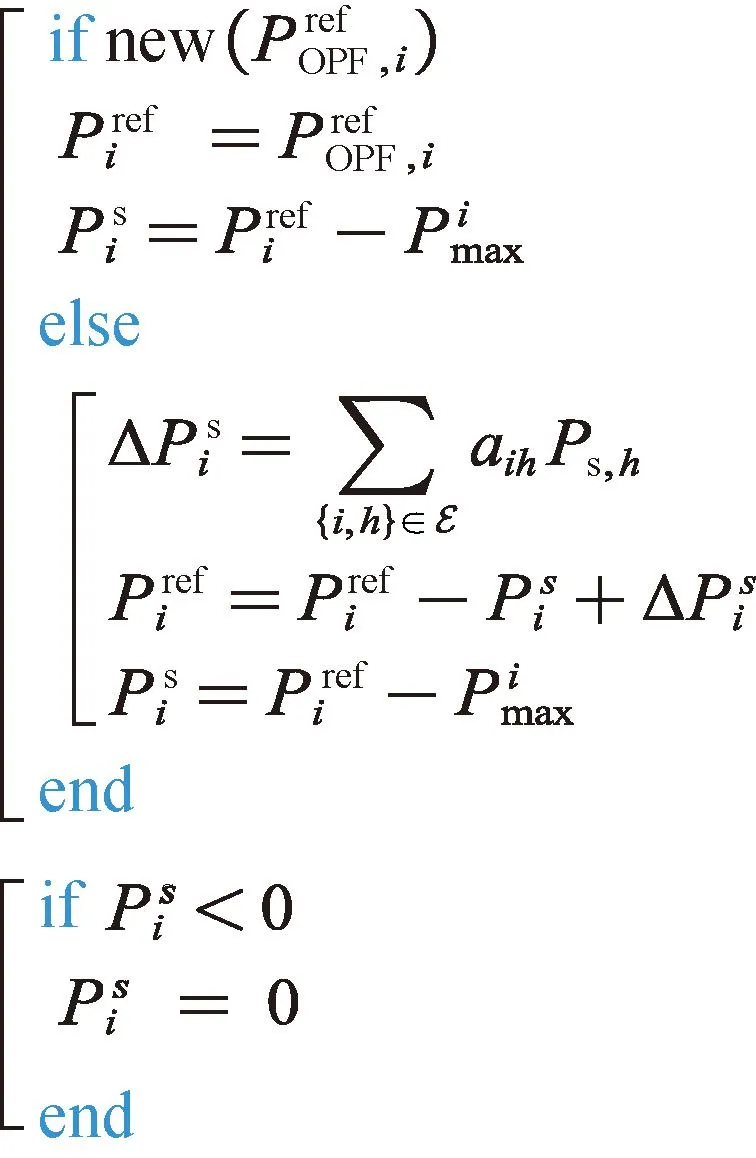
图6 i节点的调度指令更新伪代码Fig.6 Dispatching order updating pseudocode of node i

4 仿真案例分析

为了验证所提算法的有效性,本节设计了3个案例场景进行测试:测试场景1为仿射状IEEE 5节点拓扑下,不同位置单个电源发生功率偏差时的系统表现;测试场景2为标准IEEE 5节点拓扑下,不同位置单个电源发生功率偏差时的系统表现;测试场景3为标准IEEE 14节点拓扑,在模拟真实光照变化下的系统表现。

4.1 测试场景1:仿射状IEEE 5 节点拓扑下不同位置单电源容量变化

先测试结构比较简单的仿射状IEEE 5节点拓扑下的算法性能表现,拓扑结构如图7所示。各节点标准条件下光伏电源容量和负荷信息如表1所示。集中式调度算法更新周期为15 min,分布式调度算法更新周期为1 min。我们设置3处光伏电源分别在不同时间发生缺电:

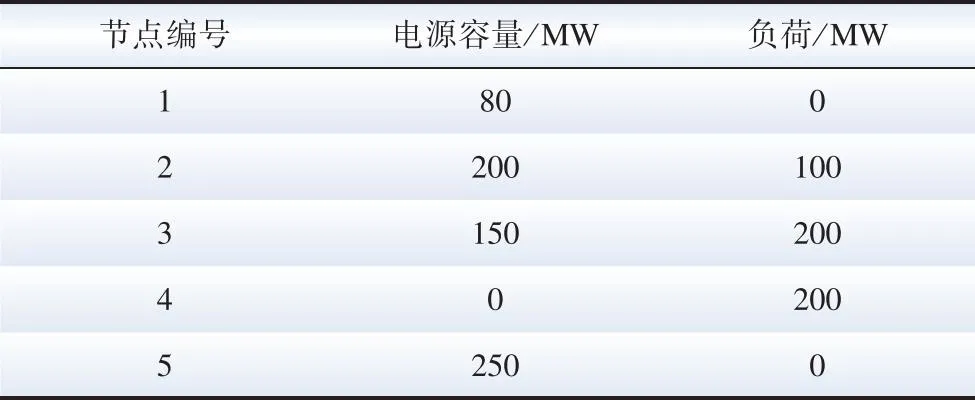
表1 IEEE 5节点拓扑电源和负荷信息Table 1 Generation and load information of IEEE 5-node topology

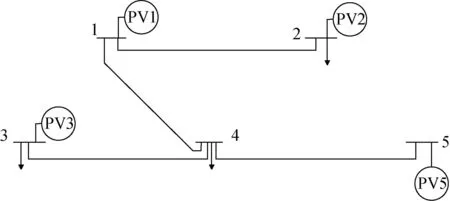
图7 仿射状IEEE 5节点电路拓扑图Fig.7 Topology diagram of affine IEEE 5-node

在16 min时,节点3处的3号光伏电源容量发生衰减至100 MW;在35 min时,节点2处的2号光伏电源容量发生衰减至150 MW;在50 min时,节点5处的5号光伏电源容量发生衰减至140 MW。

0 min时启动集中式调度算法,3 min时启动分布式调度算法。

图8所示为所提多时间尺度调度算法的系统性能表现。图8(a)中实线为调度算法给出的各电源功率输出参考指令Pref,i,虚线为各电源的可用容量Pmax,i;图8(b)为各节点电压幅值;图8(c)为各电源功率偏差Ps,i=Pref,i-Pmax,i;图8(d)为总功率偏差。

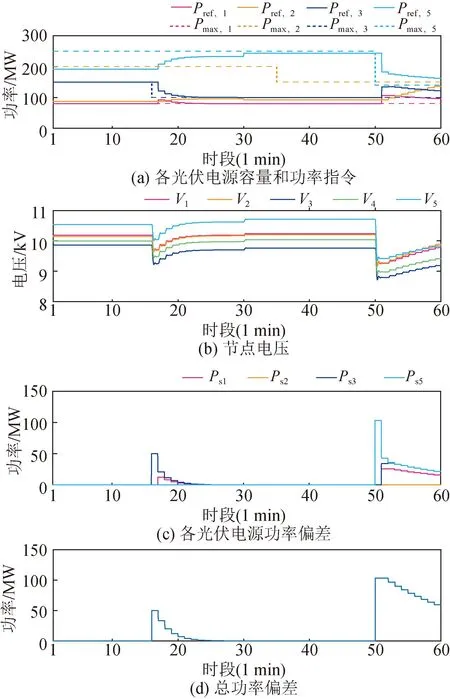
图8 所提多时间尺度调度算法系统输出性能Fig.8 System performance of the proposed multi-timescale dispatching algorithm

0 min时,各光伏电源接收集中式调度算法的功率指令,分别输出80 MW /80 MW,87.46 MW /200 MW,150 MW/150 MW,191.5 MW/250 MW,其中1、3号光伏电源满发,2、5号光伏电源有裕量。

3 min时分布式调度算法启动,因无功率偏差,各光伏电源输出功率保持不变。

16 min时,3号光伏电源发生功率偏差,其可用功率,如图8 (a)中深蓝色曲线所示,从150 MW 降至100 MW,出现功率偏差50 MW,电压发生跌落,如图8 (d)所示。同时,分布式算法执行后,各电源的功率偏差得到更新,分别为 0 MW,0 MW,50 MW,0 MW。此时总功率偏差为50 MW,如图8 (c)所示。

17 min开始,在一致性平均的分布式算法作用下,功率偏差在各节点之间平均,3号光伏电源的功率偏差值逐渐递减,2号和5号光伏电源的接受部分功率偏差而提高输出功率,如图8 (a)中黄色和浅蓝色实线所示,因两者的备用功率充足,参考输出功率可达到,所以功率偏差一直保持为零。1号电源在18 min时承担3号电源的12.5 MW功率偏差,因其已经满发,故其功率偏差为 12.5 MW。19 min开始,1号电源的功率偏差也开始和周围节点平均,由1号和5号电源消纳,故其功率偏差也逐步递减。同时,各节点电压也逐步恢复至额定值附近。

25 min时,功率偏差逐步递减至零,偏差值基本由2号和5号电源消纳,此时各电源的输出功率分别为:80 MW/80 MW,95.56 MW/200 MW,150 MW/150 MW,232.48 MW/250 MW

30 min时,集中式调度算法进行全局优化调度,各光伏电源出力调整为 80 MW/80 MW,92.26 MW/200 MW,100 MW/100 MW,243.18 MW/250 MW。

35 min时,2号光伏电源可用功率下降至150 MW,备用功率仍有富余,故功率输出保持不变,至到45 min。

上述两种缺电情况都是在总体可用功率大于负荷的条件下发生,经过分布式算法的若干次迭代后,功率偏差由存在多余功率热备的电源消纳。为了测试算法的稳定性,设计了可用功率小于负荷的情况:

50 min时,5号节点上的光伏电源可用功率减少至140 MW,产生功率偏差103.18 MW,此时电源全部容量为470 MW,负荷500 MW。同时,分布式算法更新各电源功率缺额:0 MW,0 MW,0 MW,103.18 MW。

51 min时,5号电源功率偏差和其相邻的1号和3号电源平均,由于1号和3号电源已经满发,功率偏差无法消纳,各电源缺额功率分别为:25.81 MW,0 MW,34.41 MW,43.01 MW。

52 min开始,1、3、5号电源功率偏差均逐步减小,2号电源作为1号电源的相邻节点消纳1号电源功率偏差,输出功率逐步增加。从图8 (c)可知,总功率偏差逐步减小。直至60 min,受收敛时间所限,各电源之间功率偏差仍未趋于一致,但整体的收敛趋势是不变的。

图9所示为传统的集中式调度算法系统输出性能,光伏电源输出功率每隔15 min进行调整,16 min发生光伏功率偏差,虽然由底层下垂控制进行了功率分担而减缓了电压跌落,但是各电源逐渐恢复到参考功率,等到30 min时才进行输出功率调整,50 min处亦然。

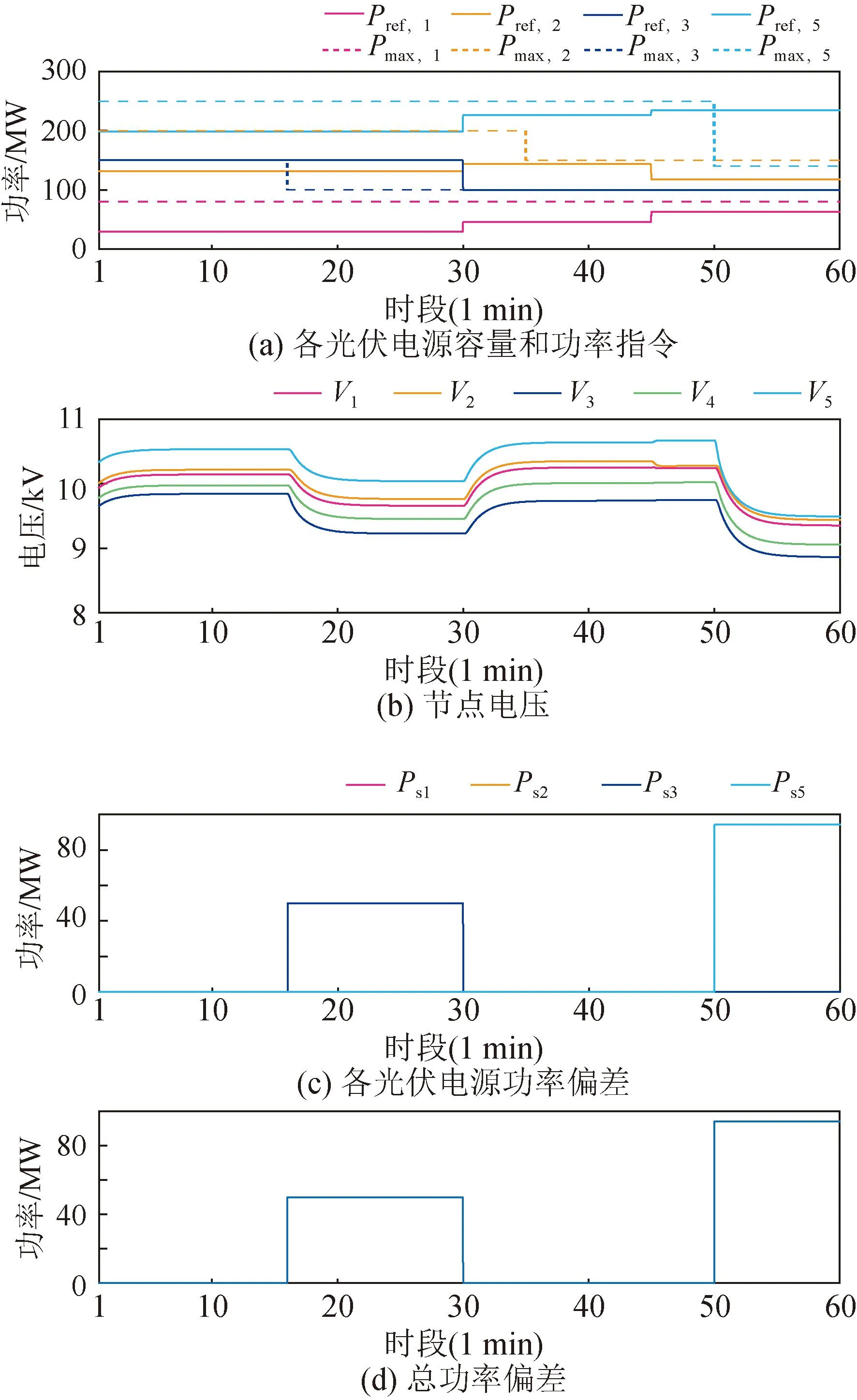
图9 传统集中式调度算法系统输出性能Fig.9 System performance of traditional center dispatching algorithm

4.2 测试场景2:标准IEEE 5 节点拓扑下不同位置单电源容量变化

本小节测试标准IEEE 5节点拓扑下的算法性能,如图10 所示,与测试场景1相比,网络拓扑存在环路而变得更为复杂,各节点电源容量和负荷,以及工况变化和测试场景1一致。

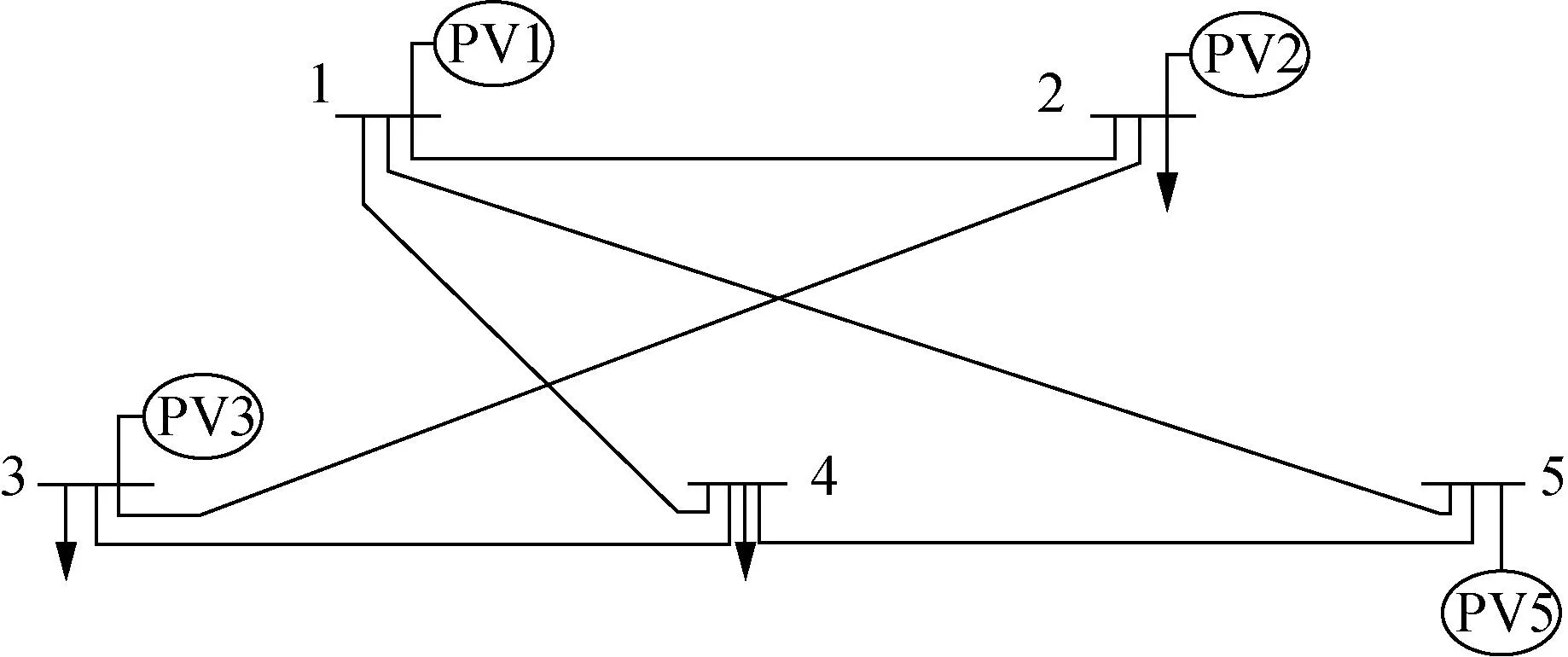
图10 标准IEEE 5节点电路拓扑图Fig.10 Topology diagram of standard IEEE 5-node

图11为所提多时间尺度调度算法的系统性能表现,各子图含义同上文。0 min时各光伏电源接收集中式调度算法的功率指令,分别输出25.21 MW /80 MW,191.06 MW /200 MW,150 MW /150 MW,138.23 MW /250 MW,其中3 号光伏电源满发,其余光伏电源均有裕量。3 min时分布式算法启动,因没有发生功率偏差的电源,电源功率指令保持不变。

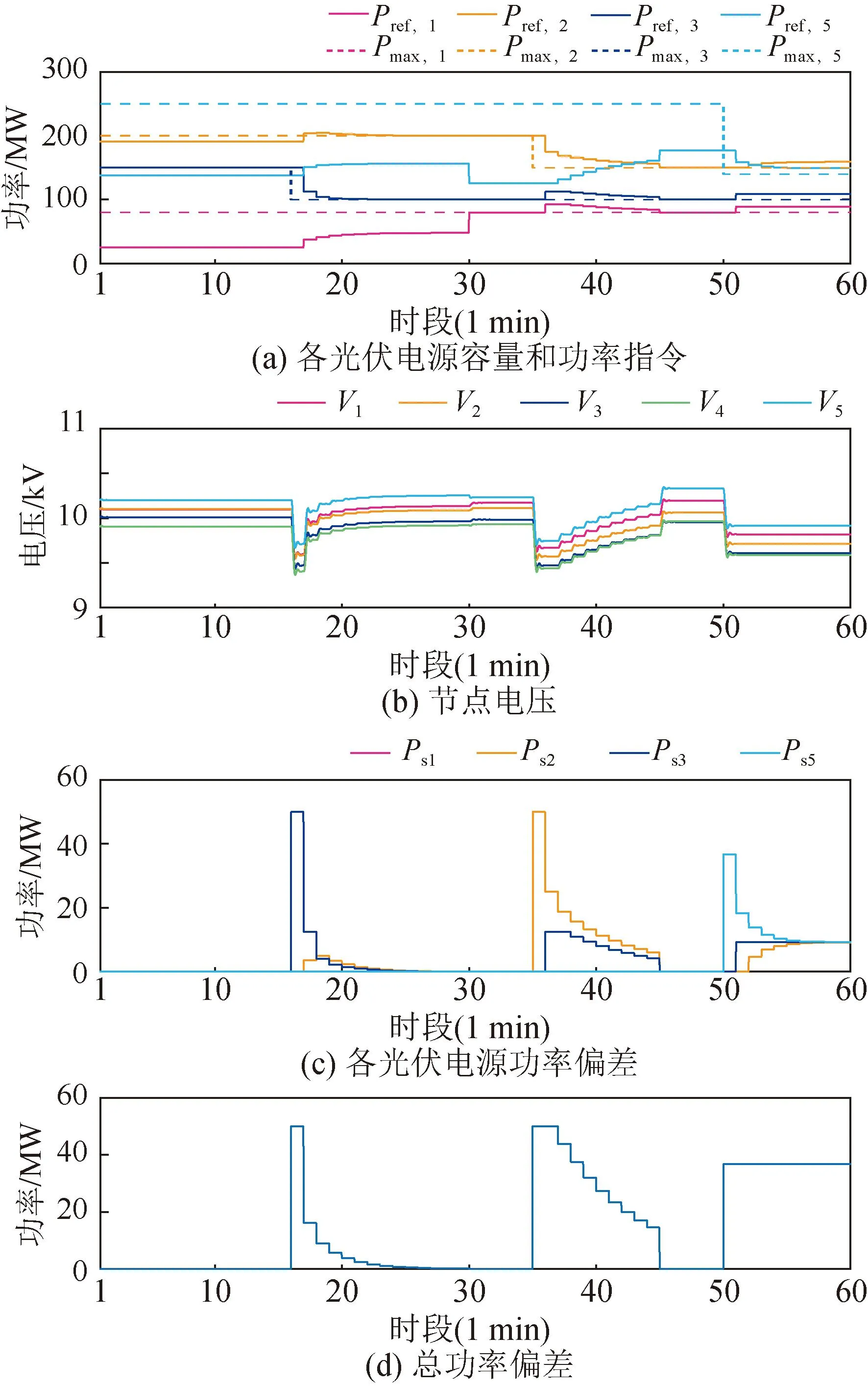
图11 所提多时间尺度调度算法的系统输出性能Fig.11 System performance of the proposed multi-timescale dispatching algorithm

16 min时,3号光伏电源发生功率偏差,其可用功率,如图11 (a)中深蓝色曲线所示,从150 MW降至100 MW,出现功率偏差50 MW,电压发生跌落,如图11 (d)所示。同时,分布式算法执行后,各电源的功率偏差得到更新,分别为0 MW,0 MW,50 MW,0 MW。此时总功率偏差为50 MW,如图11 (c)所示。

17 min时,与3号电源的功率缺额与相邻的1、2、5号电源平均,各电源参考功率分别调整为:37.71 MW /80 MW,203.56 MW /200 MW,112.50 MW /100 MW,150.73 MW /250 MW。此时,3号电源的功率偏差减小为12.5 MW,1、5号电源热备容量充足而消纳分配的功率偏差,2号电源可用容量不足,产生3.56 MW的功率偏差。之后,在分布式一致性平均算法的作用下,2、3号电源的功率偏差逐渐减小由1,5号电源消纳。

26 min时,总功率偏差接近零,此时,各电源输出功率为:47.73 MW /80 MW,200 MW /200 MW,100 MW /100 MW,156.31 MW /250 MW。各节点电压恢复至额定值10 kV附近。

30 min时,集中式调度算法进行全局优化调度,各光伏电源出力调整为 80 MW /80 MW,200 MW /200 MW,100 MW /100 MW,125.69 MW /250 MW。

35 min时,2号光伏电源可用功率下降至150 MW,产生功率偏差50 MW。分布式算法更新各电源功率缺额,如图11 (b) 所示,分别为:0 MW,50 MW,0 MW,0 MW。

36 min时,2号电源功率偏差和其相邻的1号和3号电源平均,由于1号和3号电源已经满发,功率偏差无法消纳,各电源缺额功率分别为:12.5 MW,25 MW,12.5 MW,0 MW。

37 min开始,1、2、3号电源功率偏差均逐步减小,5号电源作为1、3号电源的相邻节点消纳1、3号电源功率偏差,输出功率逐步增加。从图11 (c)可知,总功率偏差逐步减小。直至45 min,受收敛时间所限,各电源之间功率偏差仍未趋于一致,此时,进行集中式全局优化,各电源输出功率调整为:80 MW /80 MW,150 MW /150 MW,100 MW /100 MW,176.24 MW /250 MW。

上述两种缺电情况都是在总体可用功率大于负荷的条件下发生,经过分布式算法的若干次迭代后,功率偏差由存在多余功率热备的电源消纳。同样,设计了可用功率小于负荷的情况:

50 min时,5号节点上的光伏电源可用功率减少至140 MW,产生功率偏差36.24 MW,此时所有节点都达到满发,无法消纳功率偏差。

51 min开始,各电源功率偏差趋于一致,在57 min时,基本相等,各电源功率偏差均为9.1 MW左右。此后,保持稳定功率缺额和各电源功率偏差都保持不变。

图12所示为传统集中式调度算法在同样的工况下的系统输出性能。与所提控制算法相比,各光伏电源输出功率只在集中式算法运行的时候进行调整,无法实时处理光伏电源的出力缺电情况。在15.5 min,30.5 min和45.5 min,光伏电源产生功率偏差而导致电压跌落。对比图11 (c)和图12 (c)所示各节点电压的平均偏移程度,传统的集中式调度算法所示的电能质量更差。

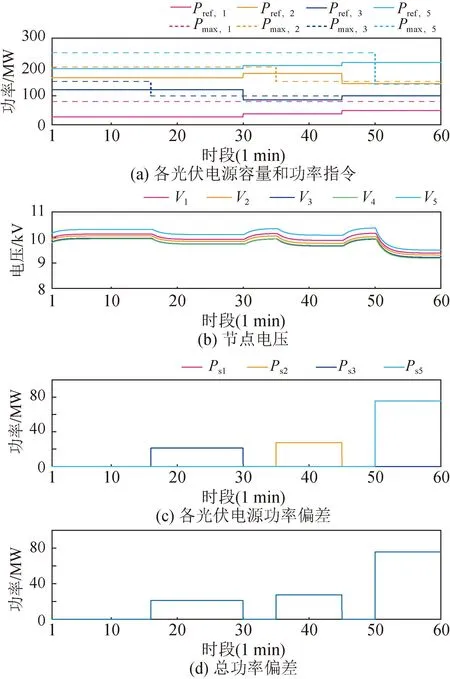
图12 集中式调度算法的系统输出性能Fig.12 System performance of traditional center dispatching algorithm

4.3 测试场景3:标准IEEE 14节点系统在模拟真实光照下的系统表现

本小节在标准IEEE 14节点拓扑下进行算法测试,IEEE 14节点网络拓扑结构如图13所示,为体现高比例直流网特性,分别在1、2、3、6、8、10号节点接入光伏电源,且光伏装机总容量大于正常负荷消耗,即由光伏电源承担全部功率平衡责任。各光伏电源在标准条件下(25 ℃,1000 W/m2)的容量和节点负荷信息如表2所示,光伏系统总容量为1 150 MW,负荷消耗为800 MW。光伏系统间信息传输拓扑为完全图,故分布式算法权重矩阵A=J6/6,J6表示全部为1的6× 6矩阵。

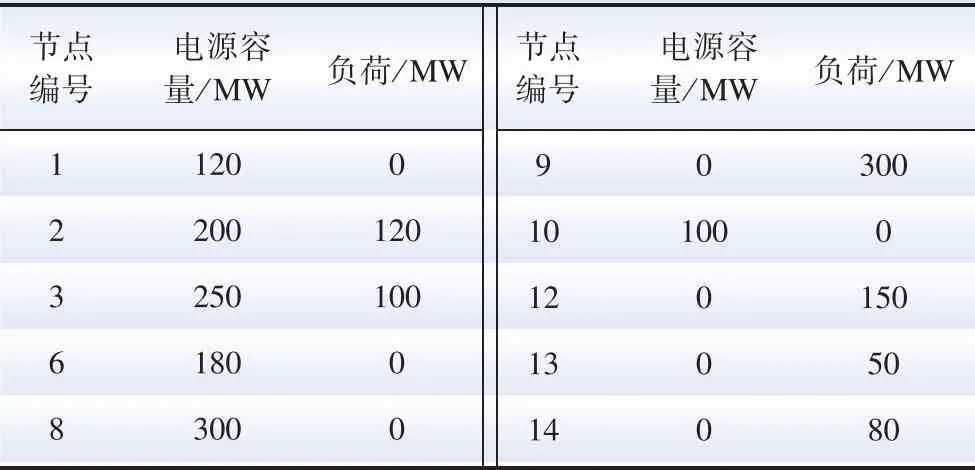
表2 IEEE 14节点系统电源和负荷信息Table 2 Power sources and loads of IEEE 14-node system

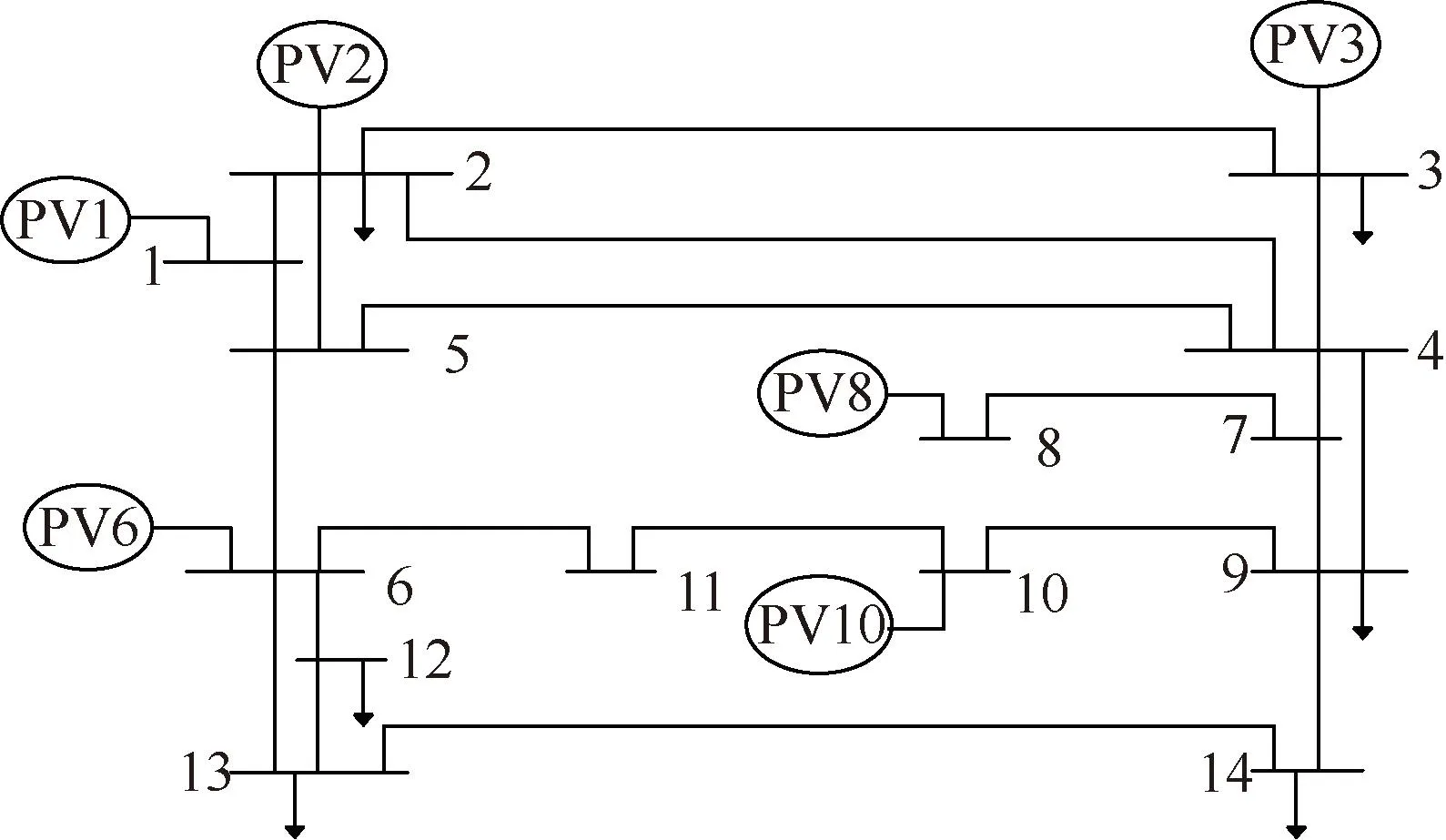
图13 IEEE 14节点直流网拓扑图Fig.13 Topology diagram of IEEE 14-node DC grid

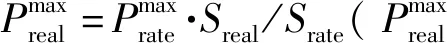
图14 各光伏电源辐照度曲线 Fig.14 The irradiance curves correspond to photovoltaic sources 1,2,3,6,8,and 10

调度算法更新周期和上文一致,集中式调度算法每15 min 运行一次,分布式调度算法每1 min 运行一次。

图15和图16分别为所提多时间尺度调度算法和考虑光伏不确定性的集中式调度算法[27]的系统输出性能。对比两者结果,从宏观角度看,因为系统运行时间长,长时间尺度上仍由集中式调度算法主导,故光伏系统输出曲线和节点电压波动曲线两者较为相似。但是,从局部短时间尺度看,特别是光伏容量减少的下行段,两者有较为明显的区别,如30 min、70 min、120 min、160 min、240 min 附近,图15 (b)中,总功率偏差在所提分布式算法的调整下逐渐减小,而图16 (b)中,两次集中式调度之间总功率偏差保持不变。为量化比较系统性能,计算了各电源平均功率偏差和各节点的电压标准差:表3所示为各电源平均功率偏差,从表中可知,所提控制算法作用下的1号和10号光伏电源平均功率偏差比对比算法略高,其余4 台光伏电源的平均功率偏差均比对比算法更小,尤其是2、3、6号光伏电源的平均功率偏差减小较为明显;表4所示为各节点电压标准差,所提多时间尺度调度算法各节点上电压标准差较对比算法有较大改善,即所提多时间尺度调度算法下系统的节点电压稳定性更好。

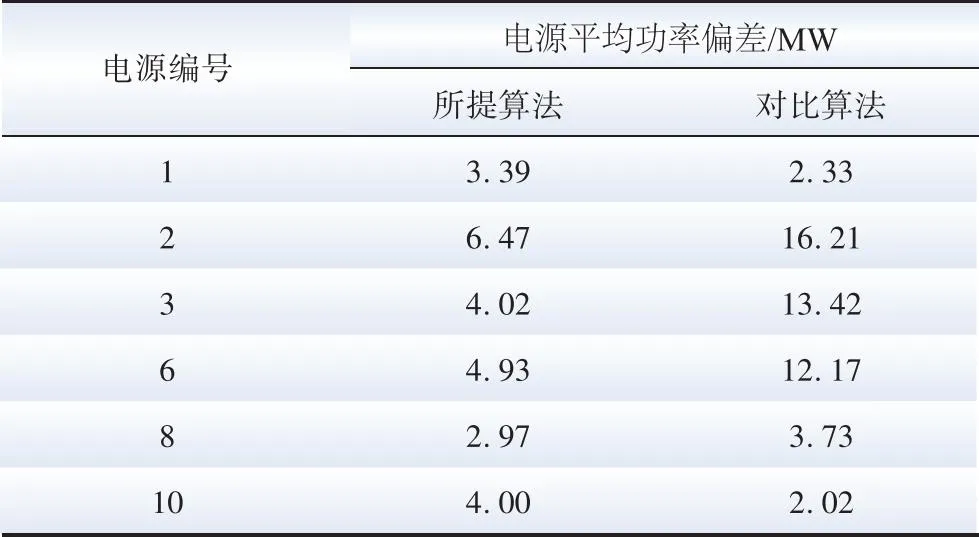
表3 各电源平均功率偏差Table 3 The average power deviation of each power source

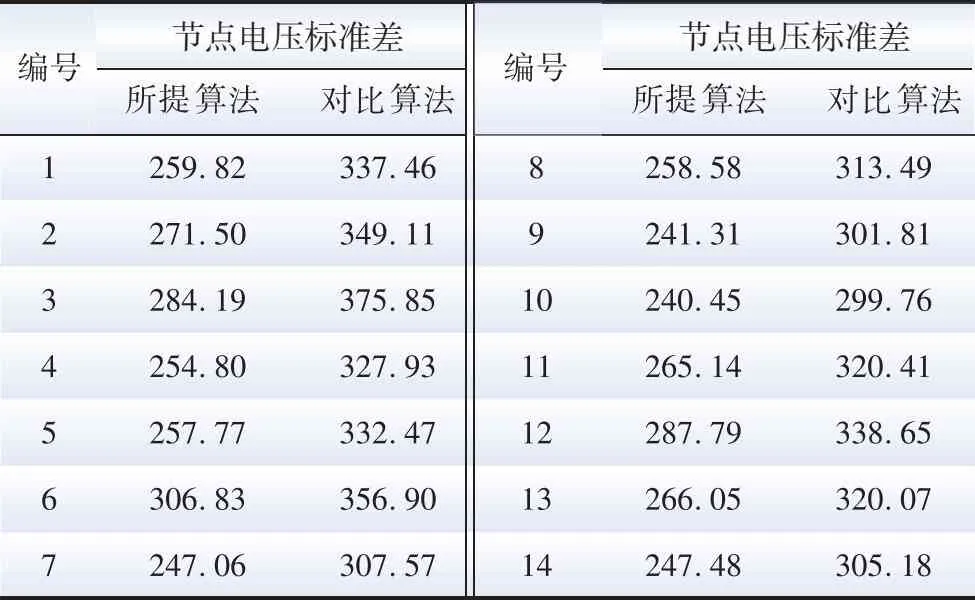
表4 各节点电压标准差Table 4 The standard deviation of voltage at each node

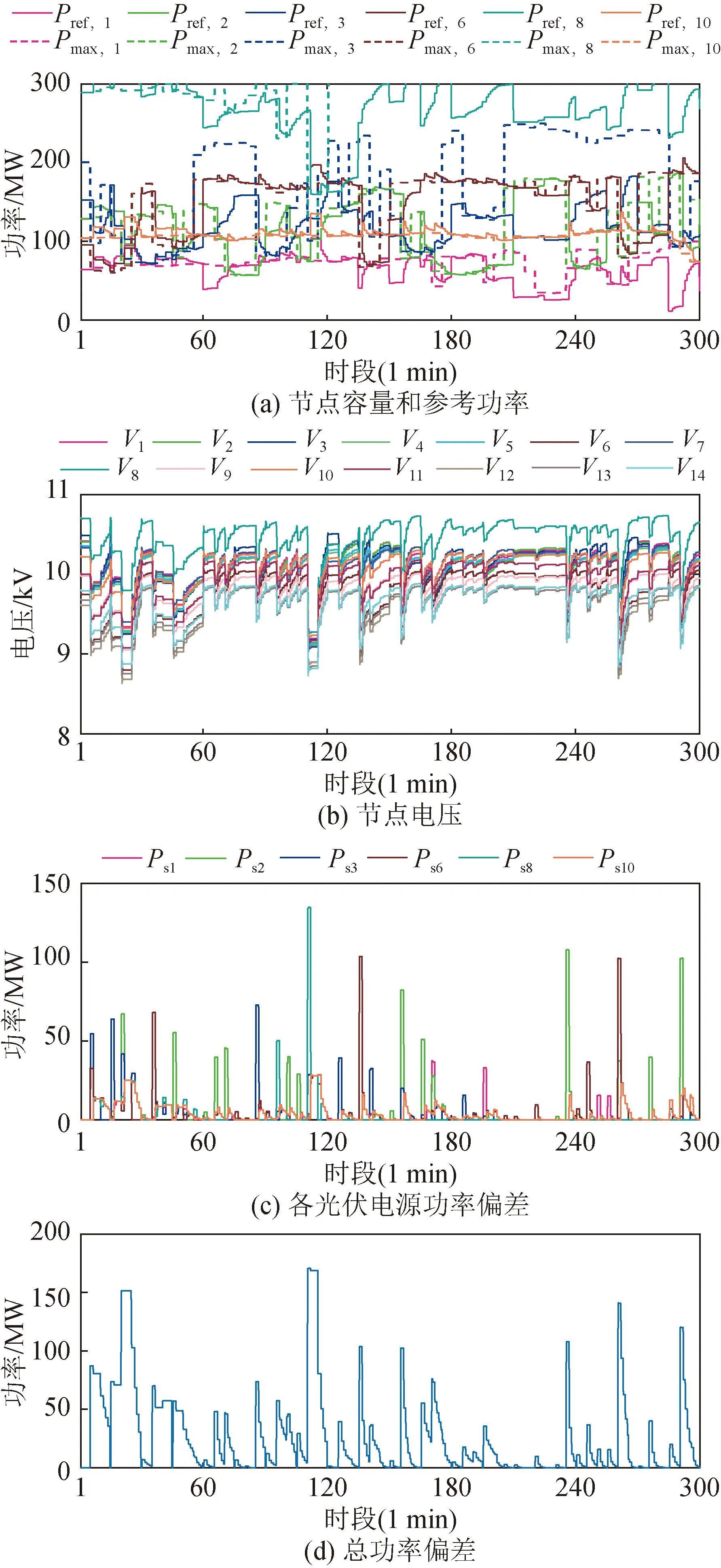
图15 所提多时间尺度调度算法在历史光照场景下的系统性能Fig.15 The system performance of the proposed multi-time scale scheduling algorithm is evaluated under historical irradiance scenarios

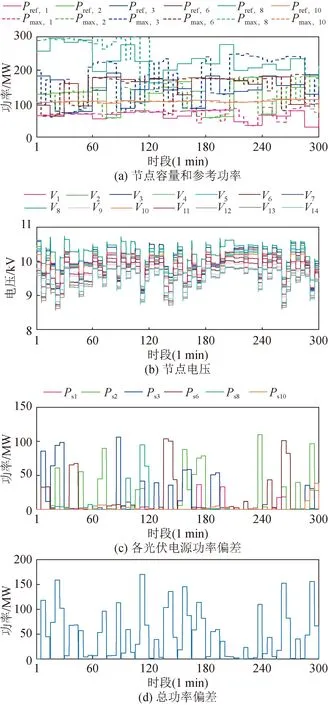
图16 考虑光伏不确定性的集中式调度算法在历史光照场景下的系统性能Fig.16 The system performance of centralized scheduling algorithm considering photovoltaic uncertainty is evaluated under historical irradiance scenarios

5 结 论

本文针对光伏系统经济调度问题提出了一种多时间尺度的调度算法,解决了传统集中式调度算法在光伏不确定性波动下的调度负担和调度实时性之间的矛盾。所提多时间尺度调度策略分为两层:第一层为在长时间尺度下的集中式调度算法,可以根据全局信息实现全局优化;第二层为在短时间尺度上的分布式调度算法,光伏电源根据相邻节点间的信息调度可用功率。建立了直流网下基于二阶锥松弛的全局凸优化模型和光伏系统间信息交换和功率调整规则。最后,在IEEE 5节点系统上进行了单电源和多电源容量变化下的仿真测试,在IEEE 14节点系统上结合历史光照信息进行了模拟真实光照环境的测试,结果表明所提多时间调度算法提升了光伏系统备用功率的利用效率,减小了各电源的平均功率偏差,而且使节点电压具有更好的稳定性。