考虑风速时空分布及机组运行状态差异的风电场有效惯量估计

李东东,张先明,姚寅,徐波,巩伟峥

(1.上海电力大学电气工程学院,上海市 200090;2.国家电网有限公司华东分部,上海市 200120)

0 引 言

随着能源供应紧缺和环境保护的重视,风力发电依靠成熟的技术和良好的应用前景在电网中的比例逐年增长。以双馈异步发电机(doubly fed induction generator,DFIG)为代表的风电依靠电力电子器件并入电网,导致机组无法响应系统频率的变化,降低了系统转动惯量水平[1-3]。为满足风电的发展要求以及避免系统频率稳定性的恶化,应充分挖掘风电机组虚拟惯量响应潜力,当前已有众多学者针对风机转子动能控制展开研究,使其具备类似同步机组惯量响应的能力,并类比同步机组摇摆方程对风机惯量水平进行估计。但仍存在以下弊端亟需解决。

其一,风速具有随机性和不确定性,大型风电场的风速分布差异性显著。导致DFIG转子旋转惯量难以实时评估。当前风场风速预测的方法分为两类:基于空间相关性和数值天气预报的机理驱动法[4],基于时间序列、概率模型和机器学习预测的模型驱动法[5-7]。文献[8]提出计及尾流效应、时延效应的风速相关性分析方法,效率高,但大规模风电场预测精度低。文献[9]基于大气数据提出数值天气预报法,通过数值计算实现场站级别风速预测,而单机计算量过大,实时性较差。对于模型驱动法,文献[10-14]提出Copula函数风速预测方法,其准确度受模型选取及精度的影响。综上,本文采用尾流效应分析相邻机组和混合Copula函数分析任意机组风速相结合的双驱动风速预测方法。在保证精度的同时显著提高预测效率,便于后续风机惯量实时在线估计。

其二,风机虚拟惯量支撑能力受外界风速和自身运行状态影响,其能量来源——转子动能直接受风速影响。低风速下受转速下限的约束,仅能提供少量惯量支撑[15],高风速下受电磁功率上限的约束,无法提供足够的额外有功功率支撑[16]。对此在中高风速下通过减载控制降低功率输出,不仅使机组具备一次调频能力,还能改善惯量响应特性[17]。文献[18-20]考虑不同风速下风机运行状态的差异,得到各风速区间内的惯量评估表达式。文献[21]提出减载控制和虚拟惯量结合的方式,能够有效减小虚拟惯量响应能量输出,避免转子失速和频率二次跌落。但未对减载控制后的风机虚拟惯量特性展开具体研究。对此本文分析不同风速区间减载控制下风机惯量响应特性的变化,并对参与惯量响应的转子动能进行评估。

其三,DFIG虚拟惯量响应时,转子转速不断下降使其风能捕获偏离最大功率点跟踪状态。捕获机械功率低于初始值并不断下降,缺额部分功率由转子动能补充,这造成了能量的损耗,使转子动能不能100%参与惯量支撑。对此,风电场惯量评估需针对虚拟惯量动态过程进行具体分析,以修正惯量估计值,对此文献[22]分析风机惯量响应过程中转子动能损失以及转速恢复阶段的动态过程,但文章后续聚焦于改进惯量控制策略以减少动能释放。文献[23]通过内电势相位运动方程,推导了异步电机的时变惯量表达式。文献[24]从机-网特性的视角,基于双馈风电机组的并网频率响应模型推导其惯量表征式。文献[25-28]从能量释放角度给出DFIG惯量时间常数表征式。以上分析都忽略了风机惯量响应时刻机组运行情况。对此,本文考虑各机组运行状态差异,对虚拟惯量动态过程进行解析,提出修正后的风电有效惯量估计方法。

综上,本文提出双驱动风速预测模型实现风场风速时空分布预测。同时,对于不同运行状态和不同控制参数下的风机虚拟惯量响应过程进行动态分析,得到风电机组有效惯量表达式。最后,结合风速预测模型实现风电场有效惯量的在线估计,为掌握风电场真实惯量响应水平提供依据。

1 双驱动风电场风速概率模型

本节采用双模型驱动方法对风电场风速概率分布展开预测。具体流程见图1。

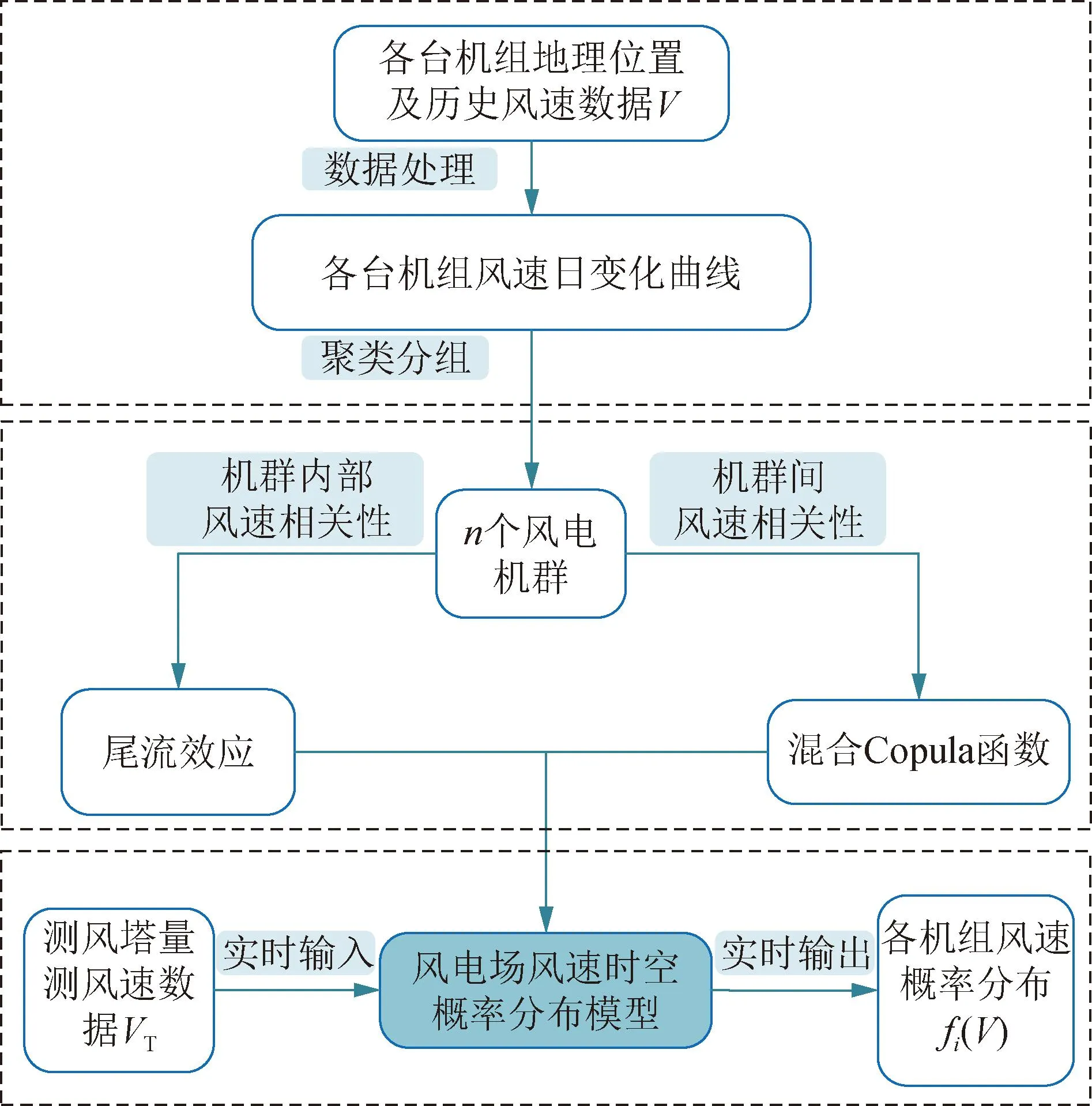
图1 风电场风速概率模型构建流程图Fig.1 Flow chart of wind farm wind speed probability model construction

风电场通常利用测风塔获取实时风速数据,测得的风速数据准确度高,能反映风电场整体风能资源大小,为构建风电场风速时空分布模型提供数据支撑。首先,对各台风机风速数据进行优化处理,并采用k-means聚类法实现风电场的聚类分区[29-31]。对于机群内部,采用尾流效应分析相邻机组间风速的相关性。对于机群之间,采用混合Copula函数拟合风电场内各机群和测风塔风速的相关性。该模型的特点在于只需输入测风塔实时量测数据,即可得到各机组实时风速概率分布。

1.1 尾流效应机理

依据空气动力学原理,下游机组受上游机组尾流遮挡,机端风速降低。这种现象称为尾流效应。伴随当前风机设计能力的加强,桨叶半径越来越大,遮挡面积增加。同时风场逐步朝着大规模级别发展。风场内部尾流效应明显。在考虑风电场内部风速变化特性时,尾流效应不可忽略,如图2所示。

图2 尾流效应原理图Fig.2 Schematic diagram of wake effect

式(1)为常规Jensen尾流模型[32]描述上下游机组间风速关联公式。

(1)

式中:VWT1、VWT2为机组WT1、WT2的机端风速;d为风速下降系数;CT为推力系数;R为叶片半径;D为两机组间隔;tanα是尾流常数,其中α为圆锥顶点系数。

图1中WT2完全处于WT1尾流效应投影范围内,但在实际运行中,由于风机地理位置以及风向的转变,大多数风机处于尾流效应部分遮挡的区域,对此,修正后的公式为:

(2)

对于上游n′台机组的尾流效应影响,下游机组j的风速受上游风机尾流效应叠加影响,如式(3)所示。

(3)

式中:Vj0为机组j未受尾流效应的风速。对于机群内部风电机组,采用尾流效应分析风速相关性的准确度较高。然而对于大型风电场,风速尾流效应叠加层次多,对于下游机组的风速拟合准确度较差,对此采用聚类方式实现风电场规模的降维处理,后续通过Copula函数预测各机群风速。

1.2 混合Copula函数

Copula函数可以实现多元随机变量边缘密度函数和联合概率分布函数的连接,能将N个随机变量的联合分布分解为N个变量各自的边缘分布以及一个Copula函数,实现变量随机性和耦合性的分离,具体分析如下。

设测风塔测量的风速为V1以及各机群中心机组构成的多维风速随机变量为V2,利用非参数核密度估计法构造边缘分布函数f(V1)、f(V2),详细过程见附录A。若F(V1、V2)为两处风速变量的联合分布函数,则存在唯一的Copula函数C(·)将联合分布函数和边缘分布函数进行连接。

F(V1,V2)=C[f(V1),f(V2)]

(4)

不同相关性分析采用不同类型Copula函数,常见Copula分类见文献[10],单一的Copula函数拟合时会出现失真,导致相关性分析误差过大,对此可将特性不同的Copula函数按式(5)组合,构造混合Copula函数提高风速预测精度。

(5)

式中:m表示Copula函数的种类,一共有M个;φm∈[0,1]为权重系数;θm为描述相关变量之间相关性的相依系数。参数的求解是构造混合Copula函数的关键。本文提出利用EM算法进行参数估计,如算法1所示。

算法1 EM法估计混合Copula函数参数输入:最大迭代次数I,相互独立的观测变量X。参数估计步骤:1.对需要估计的参数θ赋初值θ(0),进行EM算法迭代,迭代次数不能超过I。2.E步(期望步):第一轮采用θ(0),后续采用上一次M步求得的θ(t),计算隐变量z的条件概率Q(t)(z(m)|x(m);θ(t))。3.M步(极大步):根据求得的Q值,按下式更新参数θ(t+1)。θ(t+1)=argmax∑i∑z(i)Q(t)i(z(i))logp(x(i),z(i);θ(t))Q(t)i(z(i))(6)4.重复步骤2、3直至结果收敛,收敛依据为更新差值小于阈值ξ或达到最大迭代次数I:(θ(t+1)-θ(t)≤ξ)∪(t=I)(7)输出:模型参数θ。

混合Copula函数拟合精度高,但是构建过程复杂,为减小算法计算量,仅构建各机群中心机组与测风塔的混合Copula函数。利用求得的混合Copula函数并结合公式(4)、(5)可以得到测风塔风速与中心机组风速联合概率分布函数F(V1、V2),若已知t时刻测风塔风速为V1-t,则代入公式(4)后可以得到t时刻中心机组的风速概率分布函数f(V2-t)。由此获得各中心机组风速的概率分布。

综合上述两节内容,构建双驱动风电场风速时空分布概率模型,为各机组有效惯量估计提供数据支撑。

2 风机有效惯量估计

DFIG自身特性导致其惯量估计复杂,一是换流器控制策略决定虚拟惯量支撑功率大小,控制策略的灵活多变导致不能简单地通过换流器参数来估计惯量水平,二是机组惯量水平受当前外部输入和自身运行方式的变化而波动,机端风速影响最为显著。相较于同步机转子转速在±5%的范围变化,DFIG在虚拟惯量响应时转速变化范围为0.7～1.2 pu。以上这些特性都导致参与虚拟惯量支撑的能量随时间剧烈波动,风电场内部惯量空间分布的差异更加明显。

综上,从能量角度分析风电机组惯量水平是最佳选择,以风速为输入量,通过分析机组运行状态及其惯量响应过程,求解风机虚拟惯量能量波动。

2.1 DFIG运行特性分析

双馈风机捕获风能转化为机械能,拖动感应电动机旋转,输出电磁功率Pe,其中捕获的机械功率Pm由式(8)决定:

(8)

式中:ρ为空气密度;CP(λ,β)为风能利用系数,是叶尖速比λ和桨距角β的函数;λ表示叶片末端线速度与风速的比值;ω为转速;V为风速。

风能利用系数CP与λ、β详细关系如附录B所示。桨距角固定不变时,存在唯一的叶尖速比λopt使风能利用系数最大,这种运行状态称为最大功率跟踪(maximum power point tracking,MPPT)。该模式下风机既无功率备用,也无惯量支撑能力。

为使风机具备参与惯量响应和一次调频的能力。通过转子动能控制将风机转子存储的动能转化为额外有功支撑。常采用PD型综合虚拟惯量控制,控制模型见图3。

图3 风机综合运行控制框图Fig.3 Fan integrated operation control block diagram

由图3可知附加虚拟惯量控制的风机输出电磁功率由式(9)决定:

(9)

式中:Pref为正常运行参考功率;KD、KP为虚拟惯量控制比例系数;fmeas为实测频率;fref为额定频率参考值。

为保证频率数据不受杂波影响,图3中附加了低通滤波器(low pass filter,LPF)和高通滤波器(high pass filter,HPF)。图3中风机处于正常工作状态时,功率曲线按照风速范围的不同可分为启动区、MPPT区、恒转速区和恒功率区。各区间转速-功率曲线按照公式(8)推导如下:

(10)

式中:k为启动区的比例系数;kmax为MPPT区的比例系数;Pmax为最大功率;ωmax、ωmin分别为最大、最小转速。

由图3可知,除正常运行方式外,可按照预先设置的减载率δ%要求,通过超速减载或桨距角控制实现功率备用。中低风速下,转子尚未达到额定转速,通过超速减载控制,使其偏离MPPT运行点,风机转速增加,输出电磁功率减小。则减载运行下的叶尖速比δ%可利用式(11)求解:

(1-δ%)·CP(λopt,β)=CP(λδ%,β)

(11)

高风速下,为减小风力的冲击,机组通过桨距角调节实现功率恒定在最大值,此时转子转速达到最大,只能通过进一步调节桨距角大小实现功率的备用。

2.2 考虑机组运行状态的有效惯量估计

双馈风机实际参与惯量支撑的过程如图4所示。虚拟惯量响应过程中,按照用途的不同,存在3部分能量:转子释放动能ΔED(作为惯量响应的能量来源)、能量转化损失ΔELOSS、机械能损失ΔEM。故转子释放动能并未全部参与惯量支撑,对此本文定义参与实际惯量支撑的能量为有效惯量ΔEK,如式(12)所示:

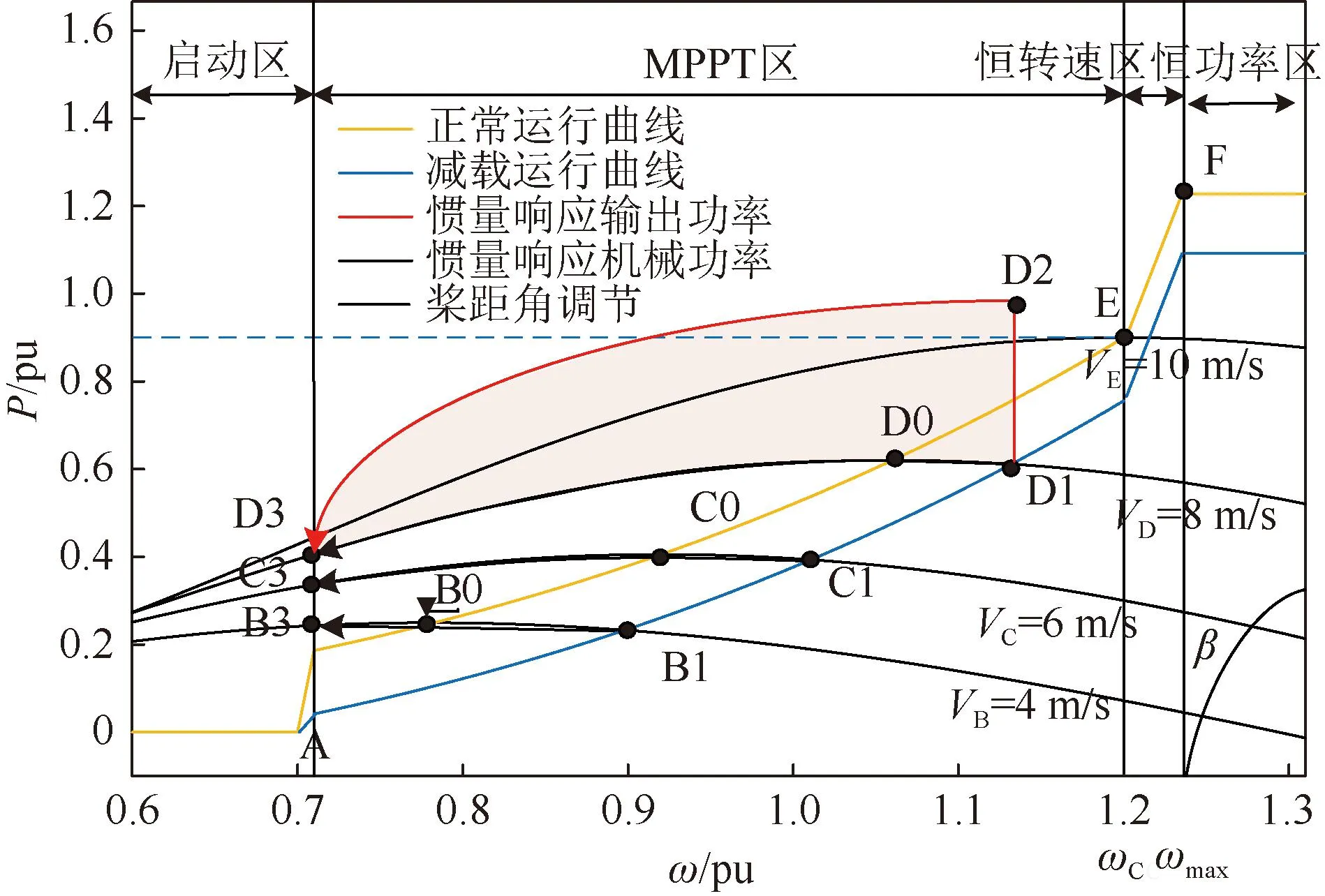
图4 风机惯量响应过程分析Fig.4 Analysis of fan inertia response process

ΔEK=ΔED-ΔEM-ΔELOSS

(12)

双馈风机惯量响应时,转子转速下降释放动能。结合图4从外部能量角度分析,转子释放动能ΔED约等于电磁功率与机械功率差值关于时间的积分,如式(13)所示。

(13)

(14)

机械能损失ΔEM是双馈风机异于同步机组的特性。即转速变化会影响机械功率的捕获,导致虚拟惯量响应时,捕获机械能减小,用于补充该部分的能量损失称之为机械能损失,计算公式如下:

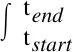
(15)

式中:Pm(t)可由公式(8)展开,与机端风速、风能利用系数相关。惯量响应持续时间一般为秒级,可认为这期间风速维持不变。风能利用系数的变化则复杂的多,对此需进一步求解分析。

以MPPT运行状态为例,桨距角恒为0。虚拟惯量响应阶段转速变化曲线通过线性拟合可得:

(16)

其中:

(17)

利用式(16)结合公式(8)中转速和叶尖速比的关系得叶尖速比时变函数如下:

(18)

在桨距角为0的情况下,将叶尖速比时变函数代入到风能利用系数表达式中。

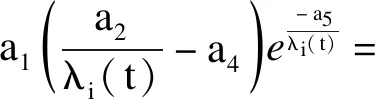
(19)

式中:CP为风能利用系数,是关于时间t和叶尖速比λ、桨距角β的函数;λi是与λ相关的中间系数;α1、α2、α3、α4、α5为相关系数。

由此得到惯量响应阶段风能利用系数时变函数。将式(19)代入到式(8)、(12)、(15)可得风机有效惯量展开解析式,见附录C。可知MPPT运行状态下有效惯量是关于风速、转速、捕获机械功率和惯量响应持续时间的函数。其他运行状态对有效惯量估计的影响分析如下。

（1）对整条光链路进行故障判断。具体方法为在两站端连接至继保装置处的尾纤头用光源和光功率计测试。一站端的尾纤头连接光源发光，另一站端的连接光功率计测试。收发两条链路都要进行检查测试，检查链路是否畅通，衰耗是否满足继保通道的需求。若畅通且衰耗满足要求，则可认定为光链路无任何问题，故障并不在通信专业的运维界面内，流程转至第（5）步；若不通畅或者衰耗不达标，则需要进行具体故障位置定位，流程转至第（2）步。

1)正常恒转速运行状态,风机脱离MPPT运行,公式(16)不再适用于推导转速与风速的关系,此时可通过线性拟合的方式解析风速与转速的关系。

2)正常恒功率运行状态,通过桨距角调节实现高风速下功率的恒定,不同风速对应不同桨距角。惯量响应时风能捕获利用系数不仅与叶尖速比有关,还需要获取桨距角大小,对此需要修正风能利用系数表达式(19),见附录C。

3)超速减载运行,该运行状态对有效惯量估计的影响为两方面,一是捕获机械功率降低,如图4中超速减载运行点B1、C1、D1纵坐标与正常运行点B0、C0、D0纵坐标对比,比例系数即为减载率。二是风机转速增加,转子动能增加。如图4中超速减载运行点横坐标所示。

4)变桨减载运行状态:捕获机械功率下降,叶尖速比脱离最优值,桨距角进一步增大。注意,高风速区正常运行时,通过桨距角控制实现功率恒定为最大值,若减载运行也需采用变桨控制,使功率恒定在次最大值,这两种运行都需要变桨调节实现,但是目标功率不同。

最后,中低风速时,超速减载运行下的机组在惯量响应时,为尽可能释放转子动能,会不断降低转子转速直到最小值;而超速减载控制下的机组在参与一次调频时,为尽可能实现持续的功率支撑,转速降低到最优转速,使其工作点由次运行点回归到最大功率捕获运行点,持续增加输出电磁功率以应对功率缺额,本文仅对风机惯量水平展开评估,因此不考虑第二种状况,超速减载只考虑转速降低到最小值这种情况。

3 仿真分析

3.1 双驱动风速预测模型分析

以某风电场38台机组为例,测量数据为各风机机端风速、转速及功率,采样间隔为10 min。各参数设置见附录D,双驱动风速预测模型步骤如下。

1)风速边缘概率分布函数。

风速的随机性使得其边缘分布函数难以用常见的分布模型进行匹配,对此本文采用非参数核密度估计法构建风速边缘概率分布函数,该方法能适应风速复杂的分布特性,结果如图5所示。

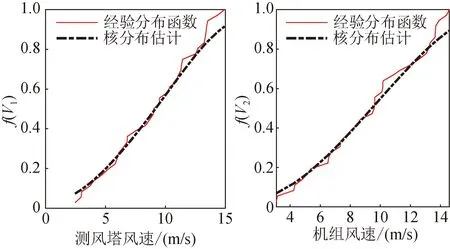
图5 非参数核密度估计对比分析 Fig.5 Comparative analysis of nonparametric kernel density estimation

2)混合Copula函数的构建。

为确定各类Copula函数对实际风速相关性的拟合效果,需绘制测风塔和机组的风速联合频率分布直方图,如图6所示。

图6 联合频率分布直方图 Fig.6 Joint frequency distribution histogram

由图6可知,风速联合频率分布主要集中在45°对角线上,表现出明显的尖峰后尾特性。表明测风塔与机组风速具备等比关系,且在高风速下具备尾部强相关性。据此,采用不同类型Copula函数进行拟合,效果如图7所示。

图7 不同类型Copula函数联合概率密度图Fig.7 Joint probability density map of different types of Copula functions

对上述四种典型Copula函数进行组合,利用本文所提EM算法估计混合Copula模型的参数,结果见表1。

表1 混合Copula函数模型Table 1 Mix the Copula function

将表1中参数值代入公式(5)中得到混合Copula函数公式,拟合结果如图8所示。

图8 混合Copula函数概率密度图 Fig.8 Mixed Copula function fitting graph

为验证混合Copula函数拟合的优越性,对不同类型Copula函数拟合效果进行比较,如表2所示。

表2 拟合度对比Table 2 Comparison of fit degree

表2中Kendall系数衡量变量间变化趋势方面的相关性程度,Speaman系数衡量不同变量间的依赖性程度。欧氏距离表示各类Copula函数与经验分布Copula函数的距离,可以衡量拟合程度的高低[34-35],相关内容详见附录E。由表2可知,混合Copula函数的Kendall系数、Speaman函数均与经验Copula函数相关系数更为接近,同时欧式距离也最小。故本文所提混合Copula函数在拟合风速相关性方面效果优异。

3)风速预测效果对比。

通过将混合Copula函数结合尾流效应可得风电场内各机组风速分布概率,取概率分布期望值为风速预测结果。将本文所提双驱动风速预测方法与仅采用尾流效应或仅采用Copula函数法获得的风速预测结果进行对比以验证预测效果。取风电场内某台机组全天风速预测结果如图9所示。

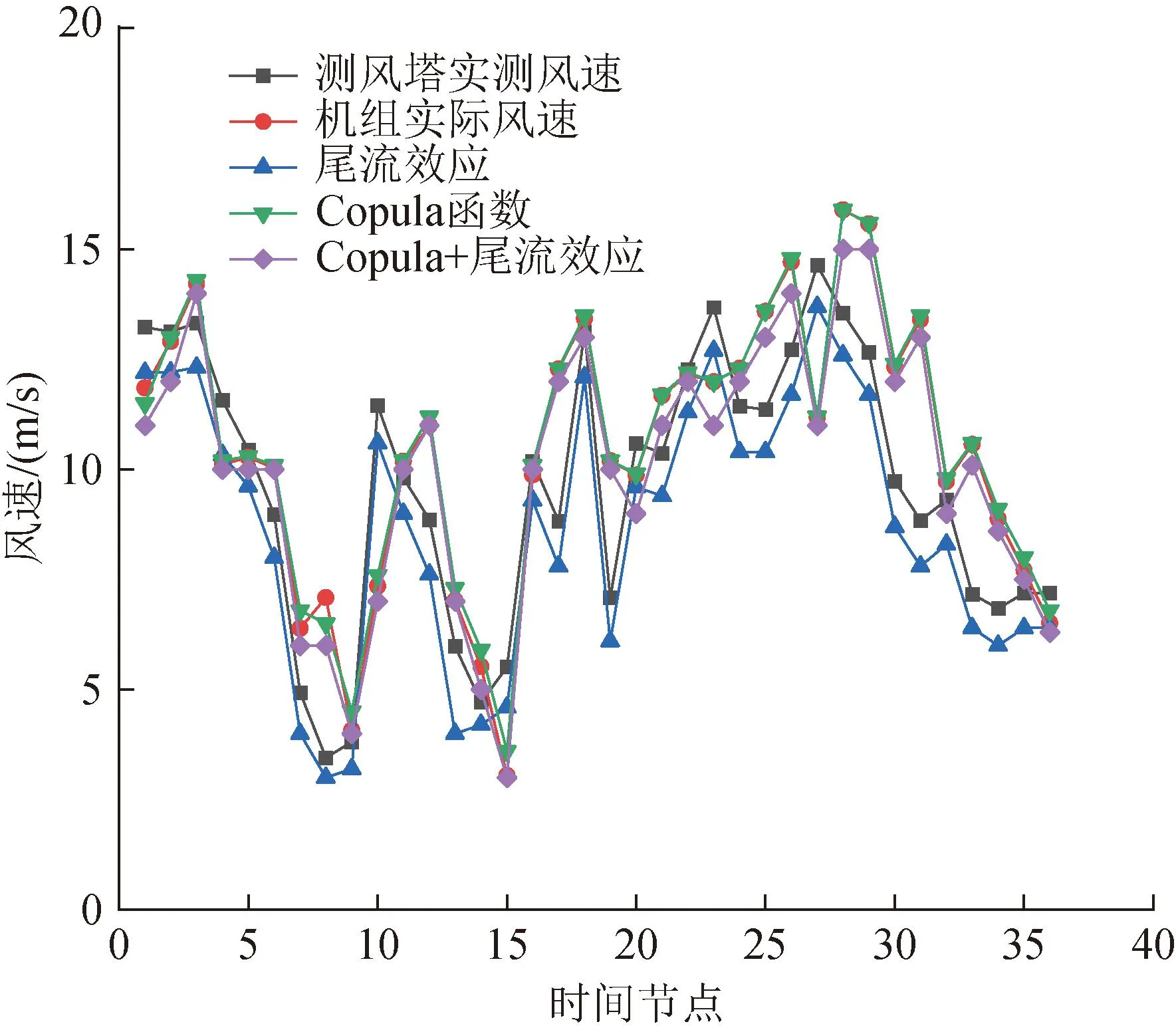
图9 不同风速预测方法对比 Fig.9 Comparison of different wind speed prediction methods

由图9可见,仅采用尾流效应的风速预测结果明显偏离实际值,而仅采用Copula函数的风速预测结果最符合实际风速。为更加直观比较不同方法的预测准确度,各时间节点预测结果误差见表3。

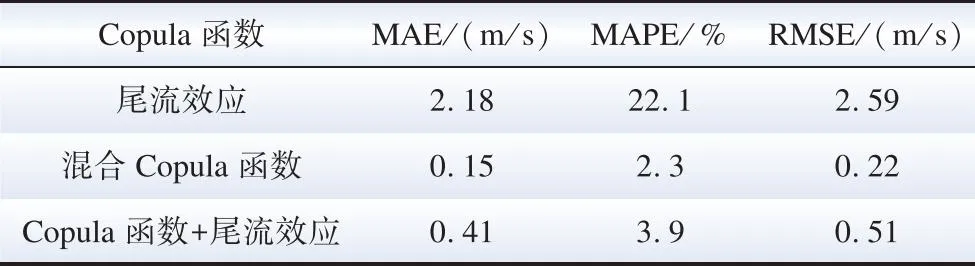
表3 预测误差对比Table 3 Prediction error comparison

预测误差分析采用平均绝对误差(mean absolute error,MAE)表示预测值与实际值之间的相似程度,采用平均绝对百分比误差(mean absolute percentage error,MAPE)表示对数据的变化敏感程度,均方根误差(root mean square error,RMSE)可以体现预测值与实际值的整体偏差。由表3可知,Copula函数法预测风速精度最高,其次是本文所提算法,但二者精度差别不大。考虑到风电场内每台机组并非都适合采用Copula函数分析,且偏远机组由于相关度较低可能无法发挥Copula函数的优势,所以仅采用Copula函数的方法不适合实际应用。同时,由Copula函数的构建流程可以看出,仅采用Copula函数预测每台机组风速会增加计算复杂度。综上,本文所提风速预测算法在保证较高准确度的前提下,能简化整体计算流程,提高计算效率。

3.2 单机有效惯量估计

本文参考simulink模块中双馈风机模型,并附加虚拟惯量控制、减载控制模块,对本文所提有效惯量估计算法进行仿真验证。分析不同风速、不同减载率下双馈风机惯量响应过程。

仿真输入风速设置为恒定值8 m/s,在tstart=5 s时设置负荷扰动,机组启动虚拟惯量响应,不同减载率下的风机输出电磁功率、捕获机械功率和转速变化曲线如图10所示。

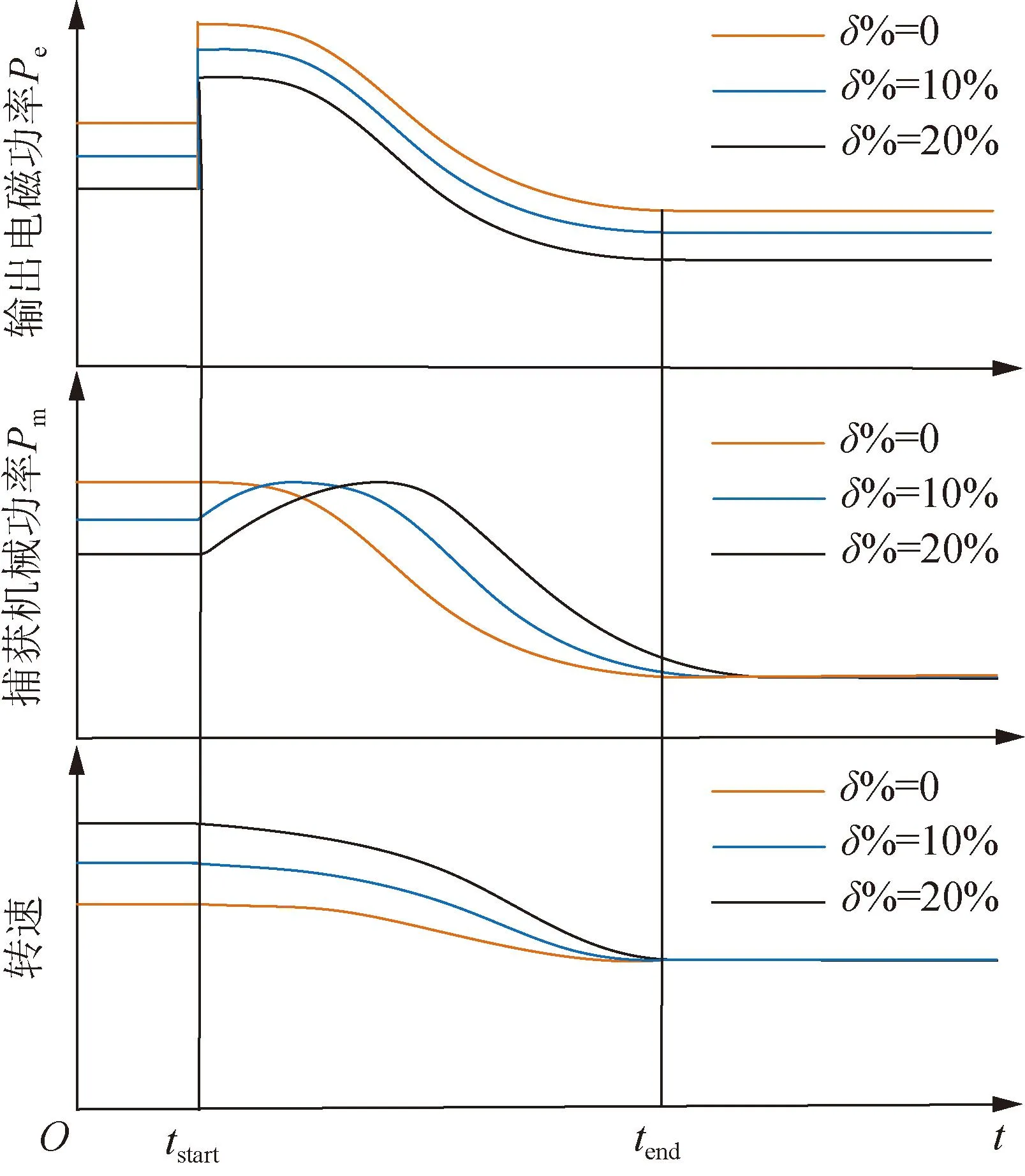
图10 惯量响应阶段变化曲线Fig.10 Phase curve of inertia response

由图10可知,与非减载运行状态(δ%=0%)相比,减载运行下,输出电磁功率和捕获功率按δ%值大小成比例缩减。惯量响应阶段,增发输出电磁功率随着转速的下降逐渐降低。而捕获机械功率在惯量响应初期呈上升变化,达到最优捕获功率值后转为下降状态,且变化程度由减载率决定。结合公式(14)可知减载运行状态下,风机捕获功率损失ΔEM小于正常运行状态。这也是有效惯量估计过程中不能忽略机组运行状态差异即减载率差异的原因。

在实际风电场中,风速不断变化,对此,改变输入风速值,通过多次重复仿真,得到不同风速下风机惯量响应中各能量值,结果如图11(a)所示。其中能量转化损失ΔELOSS无法通过数模仿真测得,只能通过实际机组实验获得,为简化分析过程,取ΔELOSS=5%ΔED。

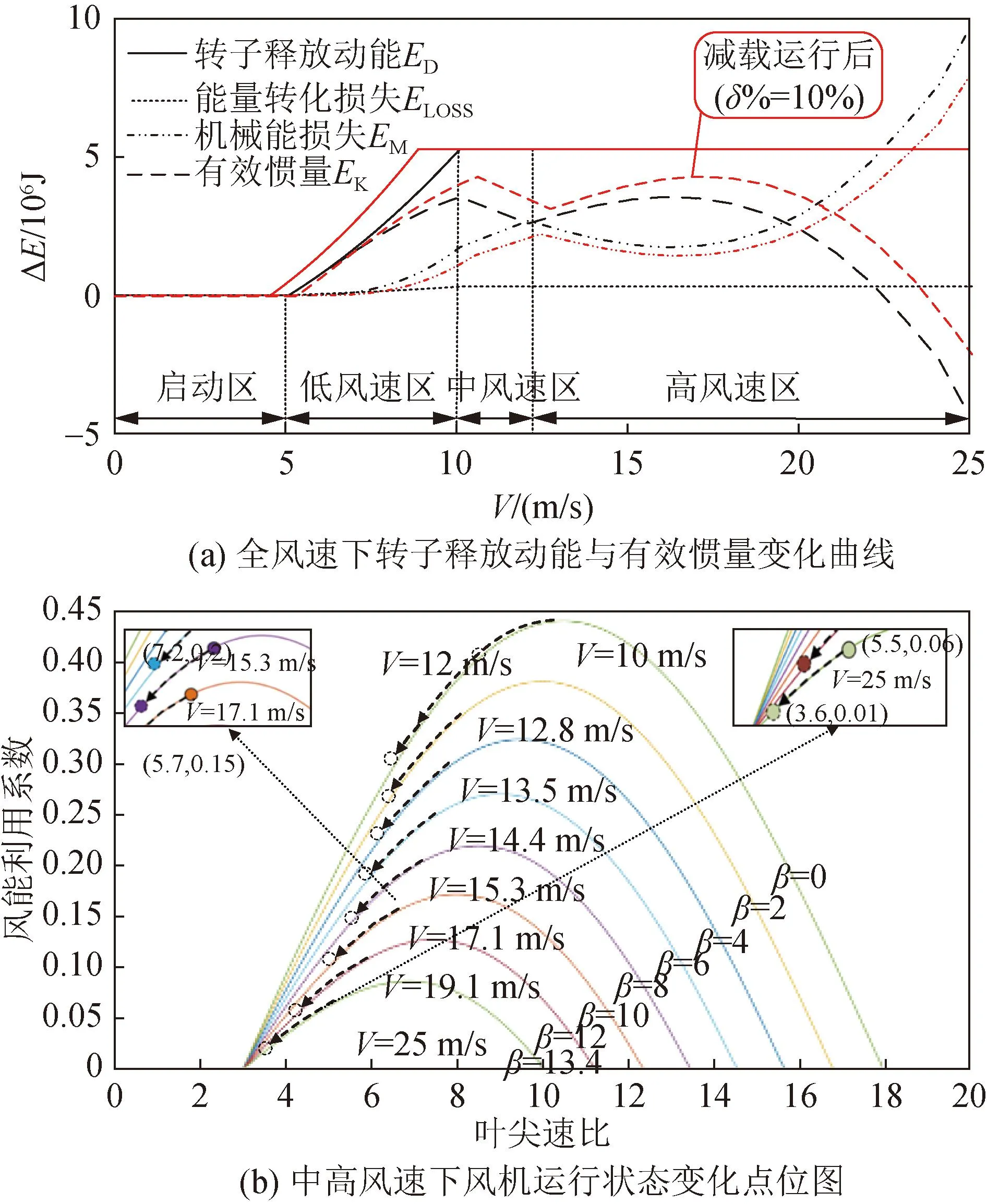
图11 有效惯量变化曲线及高风速运行点偏移分析Fig.11 Effective inertia change curve and high wind speed operating state migration analysis

由全风速下转子释放动能曲线可知,低风速区风机转子释放动能与风速呈正相关,当风速达到10 m/s,风机转子释放动能不再变化。在恒转速区机械能损失ΔEM与风速呈正比,在恒功率区ΔEM先减后增。有效惯量随风速变化特性进行分区定性分析如下:

低风速区(5～10 m/s):MPPT运行状态下风机有效惯量与风速呈现正相关特性;超速减载状态下有效惯量曲线沿风速方向平移。

中风速区(10～12 m/s):恒转速状态下,风机逐渐达到满发状态,转子转速保持不变,转子释放动能为固定值。而在惯量响应阶段,随着转速的下降,风机捕获机械功率大幅下降,导致机械能损失增加,有效惯量降低。

恒功率区(12～16 m/s):通过变桨调节维持功率的恒定。惯量响应时,风机捕获机械功率随转速的下降仍能维持在较高水平,因此机械能损失较低,有效惯量仍然继续增加。

恒功率区(16～25 m/s):风速极高,桨距角调节程度进一步增加,风能利用系数很低。此时参与惯量响应,随着转速的下降风能利用系数到达极低的水平,捕获功率降低程度较为严峻,机械能损失较大致使有效惯量不增反降,甚至低于0。

针对恒功率区下有效惯量先增后降的情况。可通过惯量响应始末时刻风机运行状态进行定量分析,以间接解释这种现象。

图11(b)中不同风速下的运行状态点对应不同颜色,右侧为初始运行点,沿箭头方向变化到终止运行点。在风速为12 m/s时,随着转子动能释放,风能利用系数由0.42降为0.30,风机捕获功率降低为初始时刻的71%;风速为16 m/s时,风能利用系数由0.18降为0.15,风机捕获功率降低为初始时刻的83%;风速为25 m/s时,风能利用系数从0.06降为0.01,风机捕获功率降低为初始值的16%。由此可推知,风速为12～16 m/s时,始末时刻捕获功率差值随风速增大而减小,机械能损失相应减少;风速为16～25 m/s时,风机终止运行点捕获功率随风速的增加而急剧减小,最小达到初始功率的16%,损失机械能持续增加,有效惯量下降。由此可解释有效惯量先增后减的特性。风速为25 m/s时,机械能损失极大,甚至转子释放动能不能弥补这部分差值,致使有效惯量为负值,说明高风速下风机调频能力较低甚至会对实际调频起负面作用。

3.3 风电场有效惯量估计

以某风电场38台机组为例,监测数据为各风机机端风速、转速及功率。采样间隔为10 min。其中,设置50%机组采用正常追踪风速变化的方式运行,另外50%采用减载控制(δ%=10%)的方式运行。

利用本文所提双驱动风速概率预测模型得到38台机组风速时空分布。并利用本文所提有效惯量与风速关系式,对考虑运行状态和不考虑运行状态两种情景下的风电场有效惯量进行估计。同时依据实际风速测量数据求解风电场有效惯量真实值,结果如图12所示。

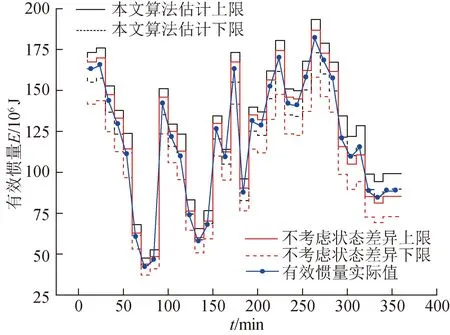
图12 不同有效惯量算法估计结果对比Fig.12 Comparison of estimation results of different effective inertia algorithms

风速概率预测模型得到的是各机组风速概率分布函数,取90%置信度下的风速预测上下限。进而得到有效惯量估计上下限。由图12可知,本文所提考虑各机组运行状态差异的有效惯量估计结果上下限都在有效惯量实际值两端,而不考虑运行状态的评估方法,出现多次实际值越限的情况,越限的次数占全部评估次数的18%,特别是在中风速时间节点评估结果越限明显。表明本文所提估计算法具备明显的保守性,有效惯量越低时,评估结果越贴合实际值。取置信度为95%时,本文所提算法估计结果越限占比仅为2%,而不考虑运行状态差异的估计结果越限占比达到31%。表明本文所提算法可有效减小估计值与实际值之间的误差,准确度较高。

4 结 论

本文提出一种考虑风速时空分布和机组运行状态差异的风电场有效惯量估计方法。通过软件仿真和实际算例验证,得到以下结论:

1) 所提双驱动风速预测模型能显著提高风电场风速时空分布预测准确度。尾流效应在分析大规模风电场风速相关性时计算简便但误差过大,MAPE达22.1;混合Copula函数拟合准确度优于其他算法,但过程复杂。将两者结合可以提高风速预测模型的有效性和应用性。

2) 本文提出的单机级别的有效惯量估计方法相比于转子释放动能方法更能表征风机实际惯量响应支撑能力。且减载运行状态下,不仅能预留有功功率,还能改善惯量响应能力,提高惯量支撑水平。

3) 场站级别有效惯量估计方法考虑了各机组机端风速和运行状态的差异,差异化评估方法贴合风电场惯量水平分布不均的特性。评估结果更符合风电场实际惯量水平,在95%高置信度情境下,评估结果越限率仅为2%,具有良好的准确度。

附录A

基于非参数核密度估计的边缘概率分布函数构造方法如下,设{zt|t=1,2,…,T}为样本空间,相应的概率密度函数为u(z),则利用非参数核密度估计的概率密度函数u(z)为:

(A1)

(A2)

式中:Ww表示函数窗宽;K(γ)表示自变量γ的高斯核密度函数。

附录B

风能利用系数CP(λ,β)与叶尖速比、桨距角的关系展开式见式(B1),绘制的三维关联如图B1所示。具有以下特性:当桨距角固定不变时,存在唯一的风能利用系数最大值;对于任意λ,随着β的增大,CP明显减小。

(B1)

图B1 风机风能利用系数三维曲面图Fig.B1 Three-dimensional surface diagram of wind energy utilization coefficient of fan

附录C

有效惯量展开解析式如式(C1)所示:

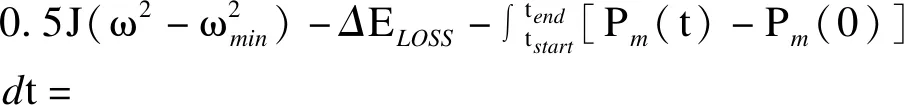
(C1)

式中能量转化损失ΔELOSS需要通过实验测得,而每次实验转子动能大小不同,转子动能转化为有效惯量的过程中的能量损失也不同,为避免每次计算都要进行实验,通过经验总结发现转化能量损失与转化能量大小有关,近似为线性比例关系,由此可通过多次实验获取平均比例系数k。则能量转化损失可转化为转子释放动能的k倍。

变桨调节控制下风能利用系数修正为下式:

(C2)

附录D

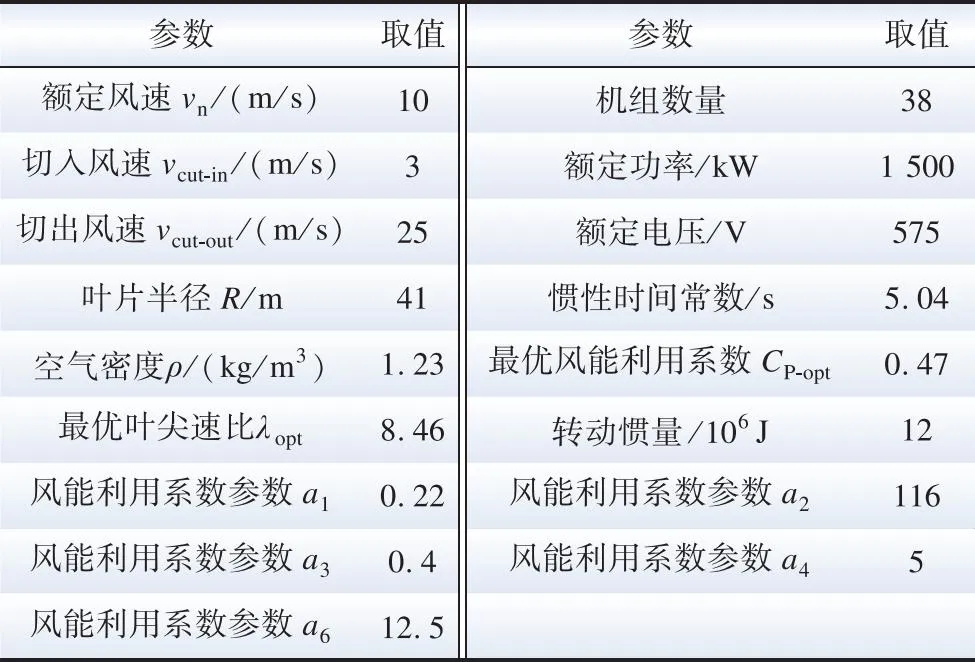
表D1 仿真算例参数Table D1 The parameters are verified by simulation and examples

附录E

经验Copula函数及欧式距离定义:

定义1(经验Copula函数):经验Copula函数由原始数据观察得到。设随机变量X和Y由S组数据构成,且其经验分布函数分别为FS(x)和HS(y),则经验Copula函数的定义式如式(E1)。

(E1)

式中:u,v∈[0,1];中间量H为判定函数,当FS(xi)≤u成立时,I[FS(xi)≤u]=1,否则I[FS(xi)≤u]=0。I[HS(yi)≤v]的判定原理同上。

定义2(欧氏距离):各类Copula函数Cp(ui,vi)与经验Copula函数间的欧式距离dC表达式如式(E2)。

(E2)

式中:p表示Copula函数的类型。不同类型Copula函数中,dC值越小说明拟合原始数据的效果越好。