基于二阶锥凸松弛的海上风电场内部无功优化

张磊,姜贞强,倪佳华,周胡,陆艳艳,项基

(1.中国电建集团华东勘测设计研究院有限公司,杭州市 311122;2.浙江大学电气工程学院,杭州市 310027)

0 引 言

能源是人类发展的最基本条件。随着经济社会的不断发展,人类对于电能的需求日益增长。煤、石油等不可再生能源的开发和使用,在为人类带来经济效益和便捷生活的同时,也给自然环境带来严重的污染和破坏。2021年4月22日,习近平主席在北京的“领导人气候峰会”上谈到中国将严控煤电项目,将“双碳”目标纳入生态文明建设整体布局[1-3]。

新能源开发与使用对推进电网的发展以及保护环境起到了不可替代的积极作用,是实现能源可持续发展战略,实现“双碳”目标的必由之路[4]。在新能源发电领域,风力发电成为仅次于水力发电之后最成熟、最具有开发潜力和最具商业化发展的发电方式[5]。其中,海上风电由于资源丰富、风速高、紊流小、发电量大,且不占用土地[6],已在全球范围内实现规模化应用[7-9]。随着风电渗透率的提高,风电将会对电力系统的安全、稳定和经济运行带来不可忽视的影响[10-13]。

海上风电场的规划、运行和调度,主要从电网可靠性角度来进行[14-18],较少从优化角度来确定风电场外送容量。由于风机有功运行在最大功率跟踪模式,海上风电场的经济运行不再是通常的经济调度问题,而是一个最优潮流(optimal power flow,OPF)问题——确定各风机最佳无功出力以最小化有功损耗。

OPF问题除了输电线路采用直流潮流方法来近似求解潮流优化外,一般性交流电网的潮流优化问题仍然是一个难以在多项式求解时间内求解的高度非线性、非凸优化问题[19-20]。对海上风电场的出力优化,启发式算法是较常采用的一类求解算法。文献[21]考虑电源、设备和过程等多约束条件,以经济性最优为目标,构建了风电场优化调度多目标数学模型;文献[22]以系统总成本最小化为目标,建立了基于多模式、双目标的调度模型,通过最优解集,为决策者提供效益最大化策略;文献[23]利用粒子群算法优化风电场内部无功,以最小化系统网损;文献[24]提出基于改进粒子群算法的海上风电并网优化算法。这些以神经网络为代表的启发式等机器学习方法,其缺陷是容易陷入局部最优,所得到的最优解不一定为全局最优。

得益于数学优化方法的进步,近年来出现了将原OPF问题松弛为凸优化问题再进行求解的方法[25]。凸松弛方法的主要思想是首先进行变量替换,其次将部分非凸约束进行松弛形成关于新变量的凸优化问题,进而求解凸优化问题的全局最优解。在精确松弛的情况下,可保证在多项式求解时间内获得原问题的全局最优解。所以,如何实现精确松弛是OPF问题求解的关键,常用的松弛方法一般有二阶锥规划 (second order cone program,SOCP) 松弛、二次凸松弛和半正定规划松弛。

目前,基于凸松驰的OPF问题主要应用在输电网和配电网侧,在风电场内部的无功优化上还鲜有应用。文献[26]利用凸松驰方法进行静态同步补偿器布点和容量规划优化。文献[27]利用二阶锥松弛技术优化新能源及负荷的不确定性接入对电力系统的影响。文献[28]则利用二阶锥规划优化主动配电网潮流。

因此,围绕海上风电场的经济稳定运行,本文基于二阶锥松弛技术建立了风电场的最优潮流凸松弛模型,在各风机有功输出最大情况下,优化其无功输出,以最优线路损耗为目标,实现总出力的最大化。

本文首先简要介绍最优潮流问题及二阶锥凸松弛方法;然后以132节点的舟山普陀风电场为实例引入海上风电场的数学优化模型,推导出基于二阶锥凸松弛的海上风电场静态工况出力优化数学模型;最后在舟山普陀风电场实际应用场景中设计算例,在四种不同工况条件下,与不进行优化的算法结果相对比,说明所提的基于二阶锥凸松弛的海上风电场静态工况出力优化算法的优势。

1 最优潮流问题和二阶锥松弛原理

1.1 最优潮流问题

最优潮流问题是电力系统中最常见的一类优化问题,是指在满足系统稳定运行和安全约束等电力网络物理约束的前提下,通过控制相关电力器件调整发电机或负荷的相关参数,使得系统总发电成本、总网损等目标函数达到最优。最优潮流问题的目标函数或约束方程通常是非线性的,优化变量可能是连续的也可能是离散的。最优潮流问题标准形式如下所示:

(1)

式中:u,x为优化变量;f(u,x)代表优化目标函数;g(u,x)表示等式约束;h(u,x)是不等式约束。最优潮流问题中的变量用于表征电力系统的运行状态,一般有:节点电压幅值和相角,节点注入有功功率和无功功率变量。

然而,由于二次潮流约束带来的非凸性,OPF问题是一个难以精确求解的非凸优化问题,在求解过程中容易陷入局部解。因此,OPF问题的高效求解依赖于凸优化理论的进步。

1.2 二阶锥凸松弛

凸松弛方法的主要思想是通过变量替换将部分非凸约束松弛成关于新变量的凸优化问题,进而求解凸优化问题的全局最优解。

采用凸松弛方法进行优化求解效率较高,且在精确松弛的情况下,可保证在多项式求解时间内获得原问题的全局最优解,其中以二阶锥规划松弛为代表的凸松弛技术目前在OPF问题求解上得到了广泛的应用。

二阶锥规划作为一种特殊的凸优化问题,具有如下的数学表达式:

(2)

式中:x为优化变量;Ai为二阶锥约束系数。二阶锥规划介于线性规划和半定规划之间,属于凸优化问题。当Ai=0时,二阶锥规划问题变成了一个线性优化;当ci=0时,二阶锥规划问题变成了一个二次约束二次规划问题。

2 海上风电场建模

2.1 海上风电场模型

舟山普陀风电场的63台风机排布如图1 (a)所示,其为仿射型结构。通过抽象建模可以得到132节点的电气拓扑结构图,如图1 (b)所示,其呈现出树状图结构。树状图中的点代表系统中节点的集合,图中的线代表系统中连接相邻节点的线路集合。现定义N={1,2,…,n}为节点的集合,E={(i,j)|i,j∈N}为线路集合,树状图的根节点代表变电站节点,节点类型为平衡节点,用序号132进行表示。将舟山普陀风电场中各个电力系统元件等值成相应的数学模型,从而建立海上风电场辐射状电力系统数学模型。

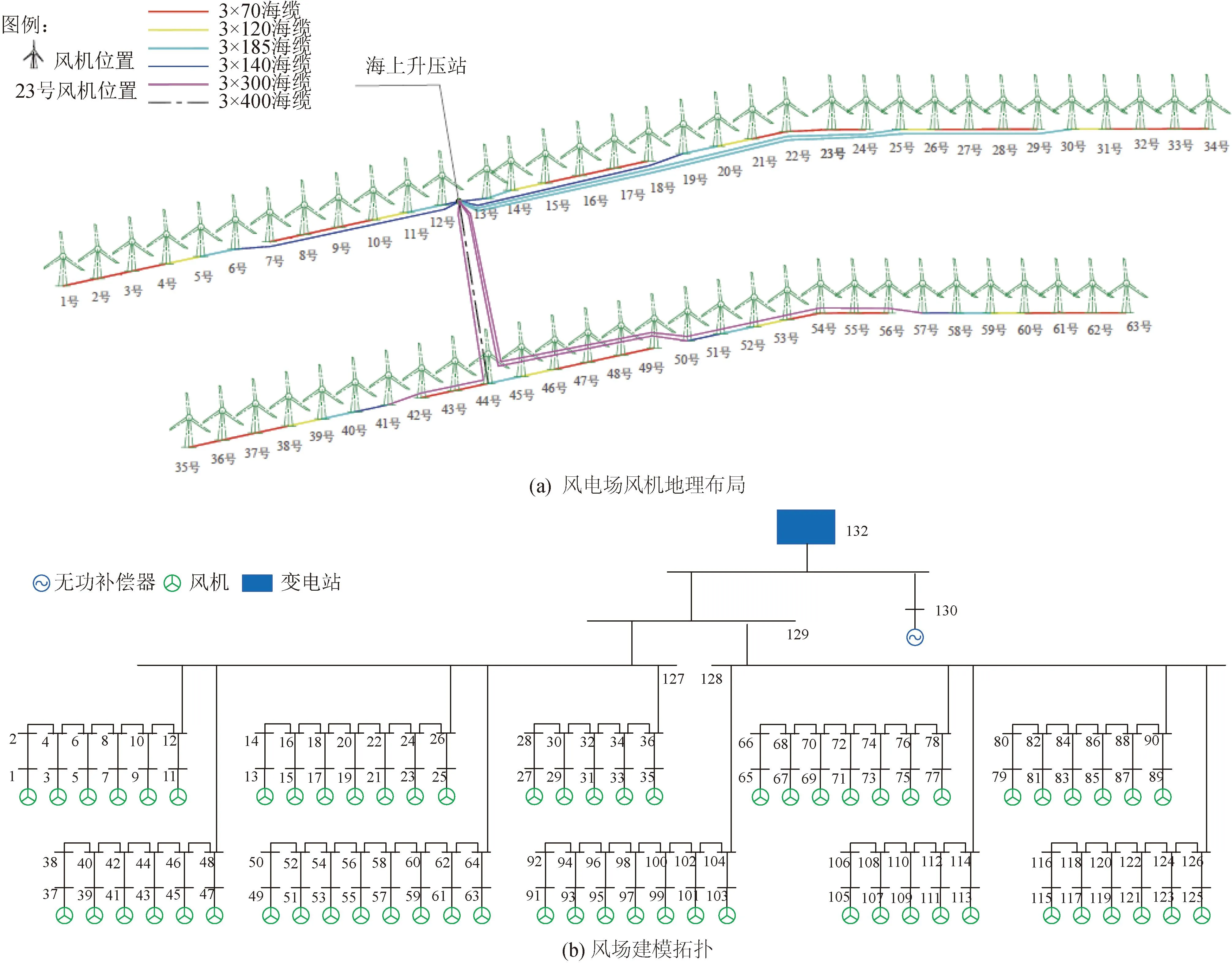
图1 舟山普陀风电场布局和拓扑Fig.1 Topology of Zhoushan Putuo wind farm

接下来将从目标函数、等式约束和不等式约束三个方面建立海上风电场潮流优化数学模型。

2.2 目标函数

海上风电场最优潮流问题的目标函数是最大化海上风电机组的净发电量,由于各风机最大有功出力是确定的,所以问题在于改善潮流,减少线路有功损耗,使海上风电场并网容量最大,目标函数为:

(3)

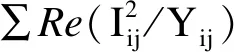
2.3 约束条件

电力系统的优化模型约束条件主要涉及潮流约束、能量约束、电压约束以及各电源的出力约束;此外,还需要考虑电力系统的网络拓扑、接线方式等。最优潮流问题的等式约束通常为非凸的潮流方程,对于一个n节点的网络,用极坐标的形式来描述:

(4)

该潮流方程等式约束聚焦于每两个节点所连接线路上的潮流方程,通过线路上潮流关系以及节点能量守恒定律构建等式约束。其中线路上流过的功率为电压与电流共轭的乘积,非凸性来源于电压与电流共轭的乘积。线路电流与所连接的节点电压之间满足欧姆定律。此最优潮流模型为支路潮流模型,如图2所示。

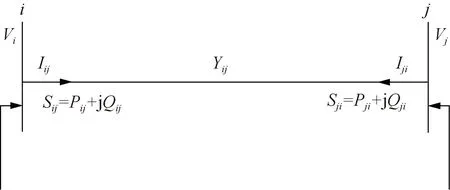
图2 潮流模型Fig.2 Power flow model

将支路潮流模型的潮流等式约束方程式(4)简写成如下数学形式:

(5)

(6)

考虑最优潮流过程中所涉及的电网稳定要求与安全裕度,不等式约束主要包括各线路传输功率容量限制、各节点电压模值范围、无功设备容量及风机出力等内容。

对于每个节点的稳态电压幅值限制约束,平衡节点的电压标么值通常固定为1 pu,除此之外的其他节点电压幅值应该保持在基准电压值的附近,电压幅值上界规定为1.05 pu,下界规定为0.95 pu。每个发电机节点发出的有功和无功功率受容量限制约束,无发电机的负荷节点的发电功率规定为0。

2.4 完整优化模型

通过建模,针对支路潮流模型,该优化问题的数学表达式为:

(7)

对于节点注入模型而言,该优化问题的数学表达式如下:

(8)

对于支路潮流模型,松弛前的海上风电场出力优化问题为等式(4)和式(6)约束的,以式(3)为目标函数的优化问题;对于节点注入模型,松弛前的海上风电场出力优化问题为等式(5)和式(6)约束的,以式(3)为目标函数的优化问题。

2.5 优化模型二阶锥凸松弛

海上风电场数学优化模型中的非线性等式约束,使得最优潮流问题为一个非凸非线性的优化问题。为了在多项式求解时间内求解该优化问题的全局最优解,采取二阶锥凸松弛方法,对非凸约束进行处理,将非凸问题转换为凸优化问题,从而通过求解松弛后的优化问题获得潮流优化解。

二阶锥凸松弛过程为:首先对变量和约束进行相应变换,其目标是将非凸潮流等式方程变成凸形式并进行相应优化求解。在变换过程中,可以将变量或相应约束条件进行松弛,将优化模型转换为凸优化问题,从而求解全局最优解。这种松弛方式虽然扩大了约束可行域,但是在精确松弛的情况下,可以在原可行域边界上得到原问题的最优解。

对于节点注入模型,定义变量Wii和Wij分别表征节点i的电压幅值变量的平方项和相邻节点之间电压变量的乘积项,用数学形式表达为:

(9)

利用新定义的变量替换等式潮流约束式(5)中的电压变量,将节点注入模型等式潮流约束变化为如下形式:

(10)

虽然式(10)解决了等式潮流约束的非凸性,但是模型中的非凸性仍然存在,对于非凸等式约束式(9),利用二阶锥凸松弛技术,松弛为如下不等式约束:

WiiWjj≥|Wij|2

(11)

则可以将非凸等式(9)进行二阶锥凸松弛得到如下二阶旋转锥,如图3所示。

图3 二阶锥Fig.3 Second order cone

对于支路潮流模型,引入如下变量:节点电压幅值平方vi和线路电流平方lij。对于等式潮流约束式(4),方程左右两边通过共轭取平方的数学变化,利用节点电压平方和线路电流平方变量将原始约束中的电压电流变量进行替换,从而将潮流等式约束表示为:

vilij=|Sij|2

(12)

(13)

将非凸等式约束式(12),利用二阶锥松弛技术,松弛为如下不等式:

vilij≥|Sij|2

(14)

其将节点电压模值平方、线路电流平方与线路复功率变量约束在二阶旋转锥中,从而构建海上风电场的二阶锥凸松弛模型。该模型通过消除电压电流中的相角信息,将潮流约束松弛为节点注入功率与节点电压平方以及节点注入功率与线路电流平方的关系。在辐射型网络拓扑中,采用反证法可以证明当负荷节点有功功率与无功功率无上界时,该二阶锥松弛为精确的,即该松弛在最优解处取到等号,因此称为精确凸松弛[29]。

对于支路潮流模型,经过二阶锥凸松弛后的最优潮流问题为:

(15)

对于节点注入模型,经过二阶锥凸松弛后的最优潮流问题为:

(16)

对于支路潮流模型,海上风电场静态工况最优潮流问题为受式(6)、式(13)和式(14)约束的,以最小化网损为目标函数的优化问题;对于节点注入模型,海上风电场静态工况最优潮流问题为受式(6)、式(10)和式(11)约束的,以最小化网损为目标函数的优化问题。利用二阶锥凸松弛技术,可快速实现优化求解,同时具有良好的收敛性能,保证解的可行性。

2.6 松弛变量还原过程

对于支路潮流模型,二阶锥凸松弛方法通过引入节点电压模值的平方与线路电流模值的平方,消除电压电流的相角信息,将潮流约束松弛为节点注入功率与节点电压平方以及节点注入功率与线路电流平方关系。松弛变量为节点电压模值平方变量以及线路电流模值平方变量,需要恢复成原始最优潮流问题的优化解。具体需要恢复的变量为节点电压模值、相角信息和线路电路模值信息,其中节点电压模值与线路电流模值均可以通过对节点电压模值平方与线路电流模值平方分别进行开根号处理,即可得到节点电压模值与线路电流模值,对于节点电压相角信息,即恢复线路两端电压差的相角信息,恢复过程如下:

(17)

式中:βij为线路两端电压的相角差,通过定义根节点的电压相角信息为零,可依此恢复其余节点的电压相角信息。

对于节点注入模型,松弛变量还原过程同理,不再赘述。

图4抽象展示基于二阶锥凸松弛的海上风电场静态工况出力优化算法流程。首先根据海上风电场的电气结构图建立标准电气模型,对相关参数进行等效计算,简化为IEEE标准拓扑结构图;其次根据标准模型建立潮流优化数学表达式(7)、(8),再对普通潮流优化模型进行二阶锥松弛得到凸优化模型式(15)、(16);然后用求解器解凸优化模型得到最优解;最后根据式(17)把松弛变量还原。

图4 算法流程图Fig.4 Algorithm flow chart

3 算例分析

3.1 模型基础

对于前述所提出的海上风电场静态工况二阶锥凸松弛最优潮流数学模型进行算例仿真测试与分析,选取的测试场景为舟山普陀风电场。仿真实验在CPU主频为3.2 GHz的第五代英特尔处理器电脑上进行,其存储内存为8 GB。采用Matlab 2019软件并嵌套YALMIP工具箱,构建二阶锥凸松弛最优潮流模型。在求解时,采用Gurobi求解器来求解最优潮流问题。

舟山普陀发电场主要包括如下电力系统元件:63台风力发电机组,每台额定容量4 000 kW;35 kV/220 kV主变压器以及220 kV/35 kV降压变压器的变压器类元件;海底电缆、电力电缆以及高压陆上架空线的导线类元件和动态无功补偿装置。风力发电机发出有功功率和无功功率,通过海底电缆和架空线传输到并网点,向电网提供能量。

每台风力发电机建模成发电机节点,可以向系统提供有功功率以及无功功率。变压器元件依据实际工程文件中的阻抗电压、短路损耗、额定容量和额定电压数据计算出相应的电阻值与电抗值。导线类元件通过工程文件中导线长度乘以单位长度的阻抗值,得到每条导线的电阻与电抗值。线路阻抗见附录表A1。动态无功补偿装置可以为系统最多提供或吸收30 MVar的无功功率。

舟山普陀风电场建模如第2节所述。设节点132为平衡节点。在进行潮流优化时,所有变量均是以标么值进行计算,系统功率以100 MVA为基准值进行标么化,电压变量模值的标么化基准值为220 kV。风速信息如图5所示,为某一历史时刻每一台风机上的测速装置记录得到。根据风机厂家的技术文件,风机的额定最大风速为12 m/s,其风速和输出功率近似为线性关系,即风机实际输出功率和额定最大功率之比等于实际风速与额定最大风速之比(Pi/Pmax=ei/emax)。

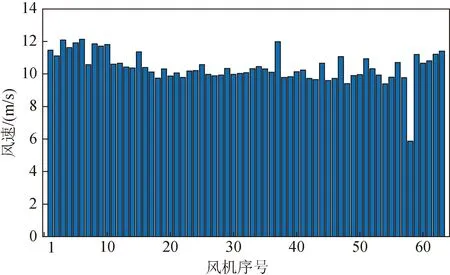
图5 各风机风速Fig.5 Wind speed of each turbine

3.2 结果对比

为表明所提基于二阶锥松弛的凸优化算法优势,将其与经典的内点法优化算法[30]、启发式的粒子群优化算法[31]进行了对比。

表1为总有功输出和网损对比,风机实际总有功输出为218.59 MW,在无任何优化的情况下,有功网损为0.98 MW,并网点输出有功功率为217.61 MW。粒子群算法优化结果网损下降并不明显,只减少了0.02 MW至0.96 MW。内点法优化算法和粒子群优化算法结果不相上下,稍优于粒子群算法,有功网损减少0.01 MW。本文所提的优化算法结果中网损下降0.55 MW(56.1%)至0.43 MW。

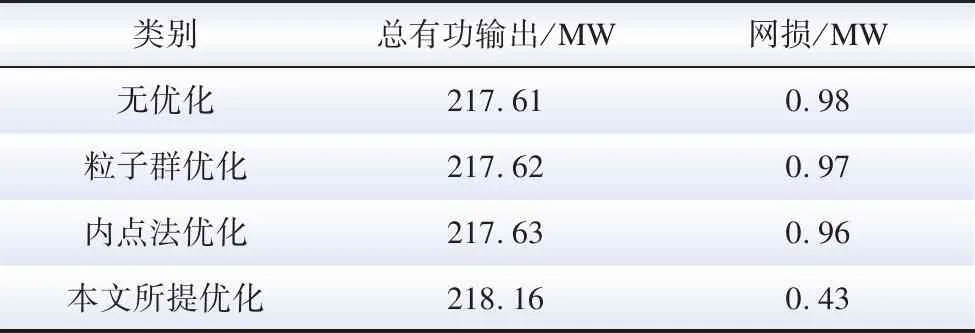
表1 优化结果对比Table 1 Comparison of optimization results

基于粒子群算法、内点法和本文所提基于二阶锥松弛的凸优化算法的各风机和无功补偿设备的无功输出值如图6所示。

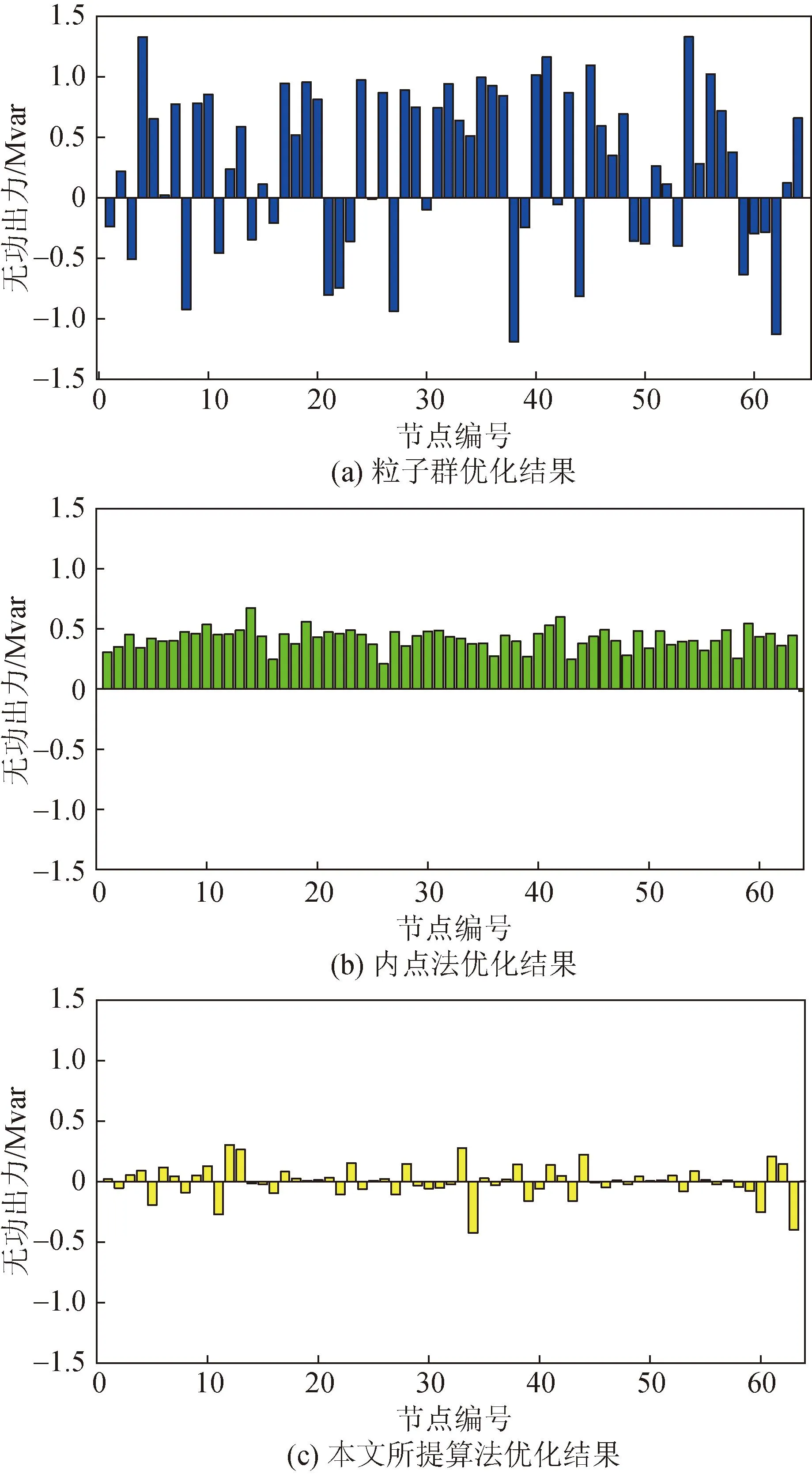
图6 无功出力优化结果对比Fig.6 Comparison of reactive power optimization results

未优化、基于粒子群算法优化、内点法优化和本文所提基于二阶锥松弛的凸优化算法的各节点电压如图7所示。其中132节点为平衡节点,其电压始终保持在1 pu,未优化前其余节点电压都小于1 pu,而基于粒子群算法、内点法和本文所提算法的各节点电压都大于1 pu,但是因潮流问题的非凸性,基于粒子群算法和内点法的优化均陷入了局部最优值,其优化结果提升并不明显,本文所提基于二阶锥松弛的优化结果取得了全局最优解,其优化效果明显。

图7 节点电压幅值优化结果对比Fig.7 Comparison of voltage magnitude optimization results

4 结 论

本文提出了风电场静态工况下的最优潮流凸松弛模型,重点研究风电场在风速一定情况下潮流优化所涉及的约束条件以及目标函数等方面的内容。通过二阶锥凸松弛数学优化方法,改善潮流,减少线路有功损耗,建立使海上风电机组净发电量最多的最优潮流数学算法。在舟山普陀风电场的真实算例中,将其与粒子群算法、内点法潮流优化算法进行了对比,表明了基于二阶锥凸松弛的海上风电场静态工况出力优化算法的优势。

本文所提算法的应用场景和缺陷:受二阶锥松弛精确性的限制,本文所提优化模型只适用于仿射网络。目前的海上风电场或大型新能源发电基地中,仍是以仿射状拓扑为主,所提模型和算法可以被广泛应用。对于存在拓扑环路的网络,需注意算法解的松弛是否依然精确。

未来研究方向:本文研究了静态风速下的无功优化问题,而实际风电场的风速是复杂而多变的,后续将考虑风速动态变化下的风电场无功优化,寻求一段时间内潮流最优,更加贴近实际需求。

附录A

表A1 海上风电场线路阻抗参数Table A1 Offshore wind farm line impedance parameters.