基于自适应虚拟阻抗的构网型与跟网型逆变器主导微网系统无功功率均分控制策略
邱晓燕,闫幸,周毅,林号缙,臧天磊,周步祥
(四川大学电气工程学院,成都市 610065)
0 引 言
随着风、光等可再生能源在电网中的大量接入,微网系统作为连接分布式发电单元(distributed generation,DG)、存储设备和负载的分布式电网,具备整合大规模可再生能源并以孤岛模式保持负载电力需求的能力,是发展“低碳”能源系统的重要组成部分。为防止DG过载与电压偏移较大,微网分层控制中要求频率与电压趋于额定值以及功率按照容量比例分配。然而,由于逆变器电源控制方式不同、容量不等、输电线路阻抗不匹配、下垂系数设置不合理等,导致无功功率难以实现均分[1-3]。其中,逆变器间的线路阻抗不匹配会造成微网中的负荷功率分配不均,从而引发环流现象[4-5],环流的存在不仅会影响负荷的均分,降低功率传输效率,还会造成系统中大量电力电子设备过热损耗,缩短设备寿命使其安全性能降低[6-7]。基于逆变器容量反比设置下垂系数实现无功功率均分可减少环流[8-9],不同逆变器根据自身容量比例提供无功功率可防止单个逆变器电源过载[9-10]。因此基于逆变器容量实现无功功率均分具有重要意义。
针对上述问题,现有方法主要包括虚拟阻抗法、电压状态观测器法、分布式一致性算法等。虚拟阻抗法一般应用于并联构网型(grid-forming,GFM)逆变器间,基于阻抗估计与环流[8,11]、偏差信息[12-14]等驱动生成虚拟阻抗项,使补偿后等效线路阻抗相等[15-16],或使线路阻抗特性满足下垂控制条件[17-19],最终实现无功功率均分。电压状态观测器法基于GFM逆变器间信息交换估计母线平均电压[20],可权衡实现电压恢复与无功功率均分。分布式一致性算法基于GFM逆变器电压与无功功率偏差生成调节项补偿至下垂控制环节[21],后续研究一般在此基础上计及额外约束[22-24]实现无功功率均分与电压恢复。上述方法中二次调节项一般补偿至GFM逆变器的电压环或下垂环节,或通过调节平均电压实现功率均分,因此难以直接应用于跟网型(grid-following,GFL)逆变器参与二次功率分配的情形[25]。
微网系统在大规模负载扰动下,仅GFM逆变器参与二次功率分配可能因调节能力不足出现电压偏移较大与过载[10]。此外,微网与分布式电源标准IEEE 1547也推荐GFL逆变器利用最大功率点剩余容量参与二次功率控制充分发挥调节潜力,通过注入无功改善电压分布[26],因此考虑GFL逆变器参与功率的二次调节具有积极意义。
基于传统控制策略的GFM与GFL逆变器由于控制方式不同难以直接实现二次功率调节的统一控制。为此,部分文献提出了应对策略:文献[27]提出在GFL和GFM逆变器控制中增加二次调节项,分别通过频率与电压偏差调节有功与无功功率,确保逆变器间功率精确分配,但其未验证即插即用与逆变器容量不等情况下所提策略的适用性。文献[28]针对孤岛微网基于电压方差调节提出了一种实现平均电压恢复和无功功率分配的分布式控制方案。然而,由于其控制目标需施加在某个DG上,由此产生的特殊性可能导致其与未施加控制目标的DG无功功率分配结果偏差较大[29]。文献[30]提出了一种考虑GFL与GFM逆变器的孤岛微网统一建模方法,基于功率解耦与扩展状态观测器(extended state observer,ESO)将不同逆变器内部动态特性与控制结构统一,最终实现电压收敛于额定值且无功功率均分;但电压观测器类方法可能因引入初值问题导致无功功率难以收敛至均分值。
另一方面,上述方法对于特定场景的适用性尚待验证[27],或依赖于过程较为复杂的非线性控制[29-30]。因此,文献[9]提出将倒下垂控制应用于GFL逆变器,使其具备类似GFM逆变器的功率下垂调节能力,从而可基于文献[21]中GFM逆变器控制策略得出全逆变器微网系统中完全协调控制GFM与GFL逆变器的主从一致性二次控制方案,实现频率/电压恢复、功率均分并抑制无功功率环流,适用于即插即用与通信退化等情形;文献[10]基于GFL逆变器倒下垂控制提出了虚拟阻抗策略用以解决因GFM与GFL逆变器间线路阻抗不匹配导致的无功功率分配问题。然而,文献[9]中主从控制方式下对主节点逆变器性能可靠性要求更高,文献[10]所提常值虚拟阻抗需预知阻抗值且无法适应线路阻抗的变化。
为解决上述问题,本文将倒下垂控制应用于GFL逆变器使其具备类似GFM逆变器的功率下垂特性;在此基础上,通过相邻逆变器无功功率偏差驱动GFM与GFL逆变器中虚拟阻抗控制环路自适应补偿异构逆变器间偏差信息,实现GFL逆变器对微网系统无功功率的主动支撑,从而使GFM与GFL逆变器间无功功率均分并实现电压恢复,增加微网的无功功率调节能力。本文的主要创新点在于:通过倒下垂控制使GFL逆变器主动参与功率的二次调节,对微网系统采用可靠性较高的对等控制,由相邻GFL与GFM逆变器无功功率偏差驱动自适应调节虚拟阻抗实现无功功率均分与电压恢复。
1 构网型与跟网型变流器主导的孤岛微网系统简介
本文研究的GFM与GFL逆变器主导的孤岛微网示意如图1所示,分布式逆变器电源通过联络线接入公共连接点(point of common coupling,PCC)共同向负载供电。其中DG1采用的构网控制方式为下垂控制,输出特性表现为受控电压源,DG2采用的跟网控制方式为倒下垂控制,输出特性表现为受控电流源[31]。

图1 GFM与GFL逆变器主导的微网系统示意Fig.1 Microgrid system dominated by GFM and GFL inverters
图1中,负荷1为6 000 W+6 000 var,其他电路参数如表1所示。
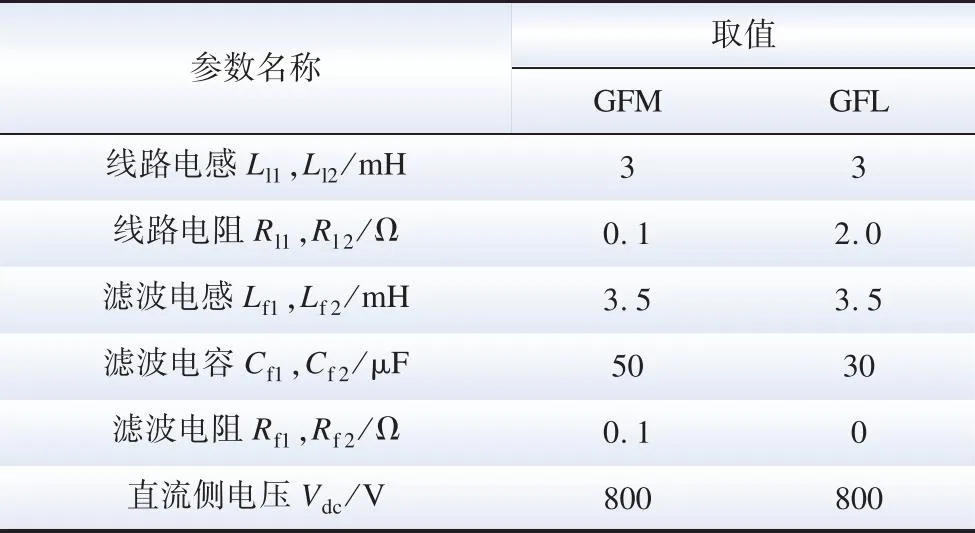
表1 GFM与GFL逆变器主导微网电路参数Table 1 Parameters of microgrid system dominated by GFM and GFL inverters
1.1 基于下垂控制的GFM逆变器
GFM逆变器下垂控制包括有功-频率与无功-电压控制[32-33],可表示为:
ω1=ωref-m1P1
(1)
V1=Vref-n1Q1
(2)
式中:ω1为角频率;V1为电压幅值;ωref和Vref分别为角频率与电压幅值的参考值;m1和n1分别为GFM逆变器频率-有功、电压-无功下垂系数;P1与Q1为输出功率。
GFM逆变器电压角度、角频率与频率关系为:
(3)
式中:φ1为电压角度;f为频率。
式(1)—(3)可实现GFM逆变器的基本控制。整体控制框图[9]如图2所示,含*变量为未滤波值。其中一阶低通滤波器可表示为:
(4)
式中:L(s)为一阶低通滤波器传递函数;ωf为截止频率。
1.2 基于倒下垂控制的GFL逆变器
GFL逆变器基本控制中的同步坐标系锁相环(SRF-PLL)可表示为:
(5)
式中:θ为GFL逆变器的锁相角;ω2为对微网q轴电压锁相得到的角频率;kppll与kipll分别为PI控制的比例和积分系数;vq2为输出侧q轴实时电压值;s为拉普拉斯算子。
借鉴同步发电机组的一次调节原理参照GFM逆变器引入倒下垂控制。倒下垂控制与dq轴参考电流可表示为:
(6)
(7)
(8)
(9)

综上,基于倒下垂控制的GFL逆变器控制框图[9]如图3所示。与前述1.1节相比,GFM逆变器通过测量输出功率并发送频率和电压参考信号,而GFL逆变器与之相反,两者表现出对偶特性[34]。
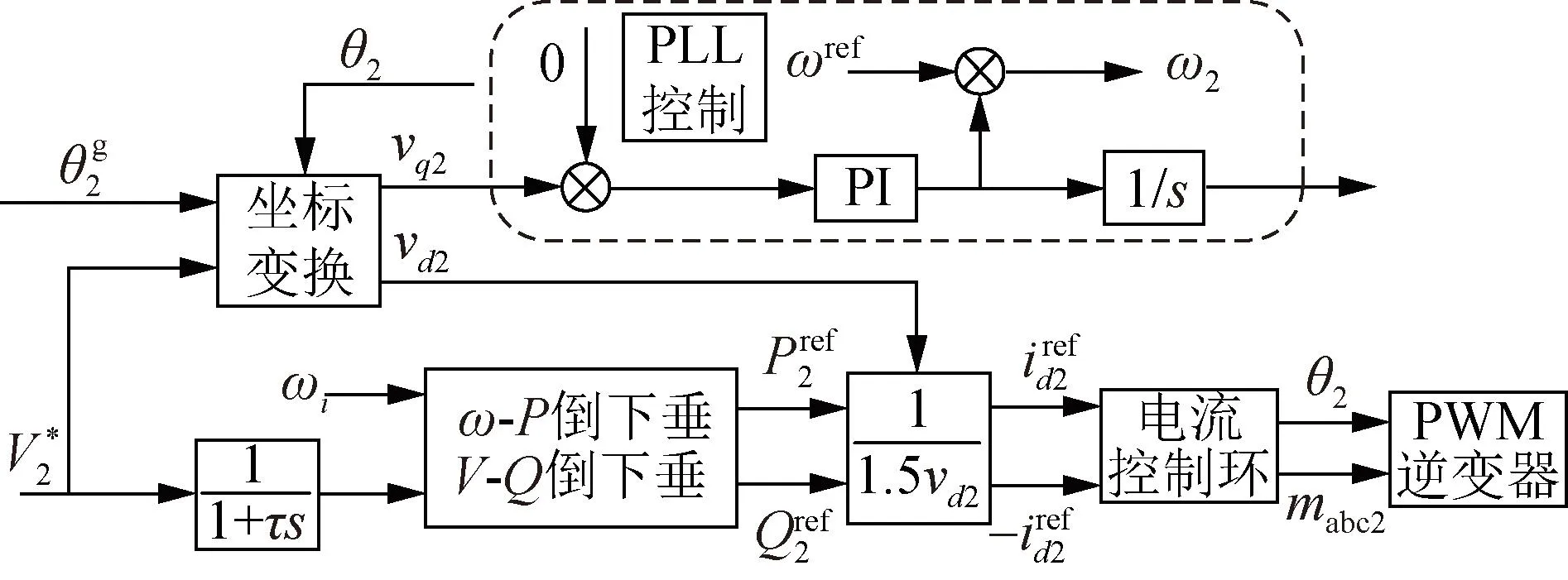
图3 GFL逆变器控制框图Fig.3 Control block diagram of GFL inverter
2 线路阻抗与无功下垂系数对无功功率分配的影响
对于图1所示GFM与GFL逆变器主导微网系统,以功率容量相等为例,无功-电压下垂系数相等时,实现无功功率均分需GFL与GFM逆变器满足下式:
Im[V1∠φ1·(I1∠δ1)*]=Im[V2∠φ2·(I2∠δ2)*]
(10)
式中:Vi为逆变器输出电压有效值,i=1,2;Ii为输出电流有效值,i=1,2;φi与δi分别为输出电压与输出电流与公共连接点间夹角,i=1,2。
当线路阻抗不匹配时,无功分配情况可描述如下:
(11)
式中:VPCC为公共点电压有效值;Xi为线路感抗;Vref为电压参考值;ni为无功-电压(倒)下垂系数。因VPCC和Vref远大于Xi,线路阻抗不匹配加重了微网无功功率分配不均的效果,甚至可能会导致系统失稳[35]。
实际运行中,由于各逆变器电源到母线处的线路阻抗不相等,导致式(10)难以满足,使得逆变器间无法按照容量比实现无功功率均分。此时调节无功下垂系数可改善无功功率分配,如图4所示,其中下标1为GFM逆变器,下标2为GFL逆变器。当n>n′时,ΔQ′>ΔQ,ΔV>ΔV′,表明下垂系数越大无功功率越趋于均分,但电压越偏离额定值,且过大的下垂系数会恶化系统稳定性[35],因此精确的无功功率均分需另寻控制策略实现。
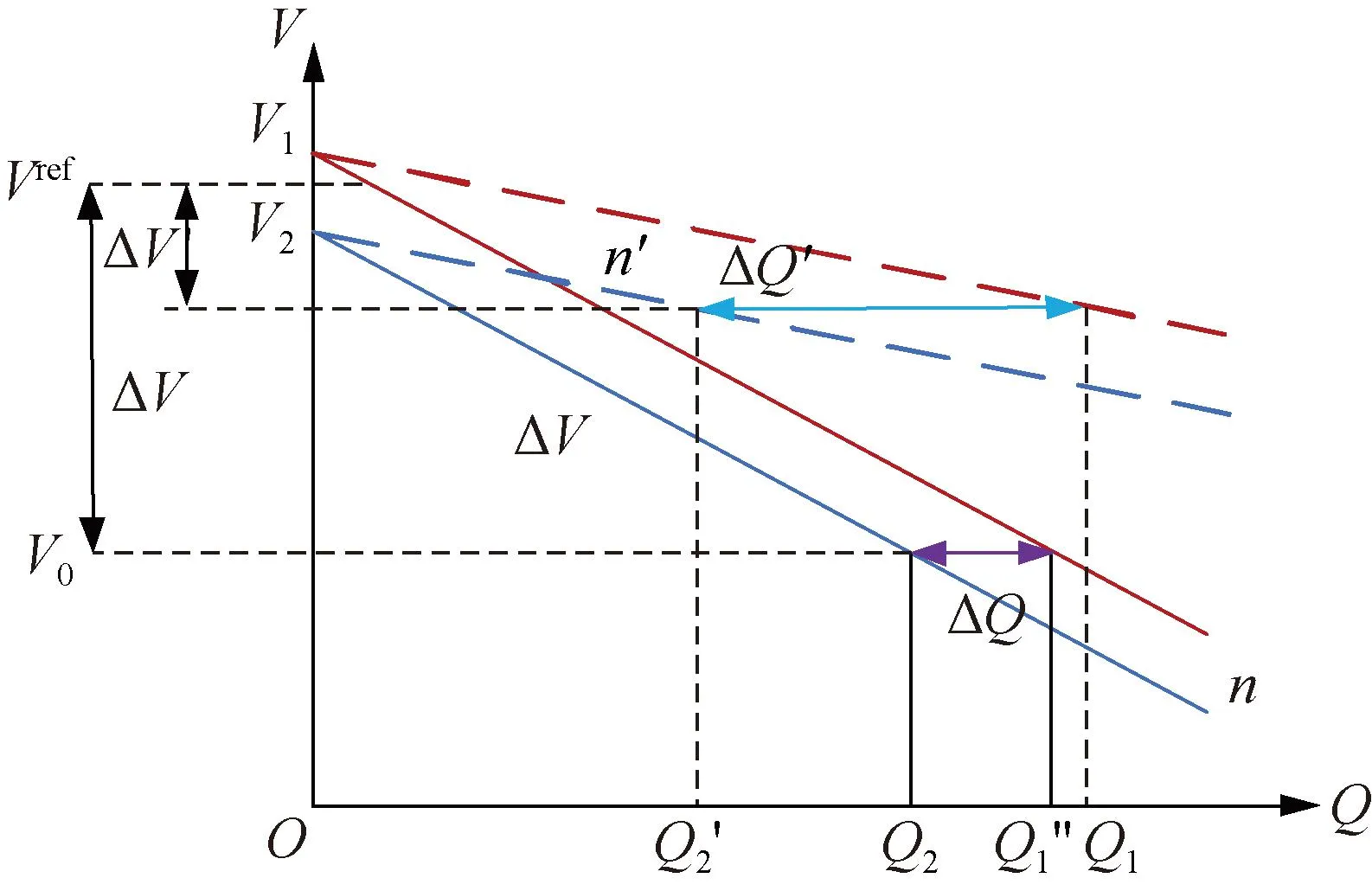
图4 调节无功下垂系数改善无功功率分配Fig.4 Adjust reactive parameter to regulate reactive power sharing
3 基于自适应虚拟阻抗的跟网型与构网型逆变器无功均分策略
3.1 虚拟阻抗控制原理
针对逆变器并联时线路阻抗不匹配导致的输出侧电压与无功分配偏差问题,可通过虚拟阻抗法[17]解决。其原理如图5(a)所示:设GFM逆变器(DG1)与GFL逆变器(DG2)容量相等,线路阻抗Zl2>Zl1,A点与B点因阻抗不匹配导致无功分配不均,通过对线路2引入虚拟阻抗Z*使B*处电压与A处接近以补偿因阻抗不匹配产生电压降同时抑制环流,最终实现无功功率均分。其控制过程如图5(b)所示。

图5 虚拟阻抗控制原理Fig.5 Principle of virtual impedance control
3.2 适用于GFL与GFM逆变器主导微网系统的自适应虚拟阻抗控制策略
由于实际微网中线路阻抗难以测量且一般不相等,补偿常值虚拟阻抗已不再适用,因此考虑基于分布式一致性自适应调节[36]无功功率偏差的自适应虚拟阻抗策略。
广义上的无功功率均分可表示为:
niQi=njQj
(12)
式中:ni/j为电压-无功(倒)下垂系数;Qi/j为逆变器输出无功功率。每个DG的无功功率控制器在比较本地与邻近逆变器无功后生成无功功率偏差:
(13)
式中:aij为反映邻接矩阵中通信链路连通变化条件的元素,相连为1,否则为0;Ni为可与第i个逆变器通信的逆变器集合。
(14)
式中:δQi为基于相邻逆变器无功偏差经积分生成的补偿量;kQi为无功偏差积分系数。所提出的自适应虚拟阻抗控制如图6所示。
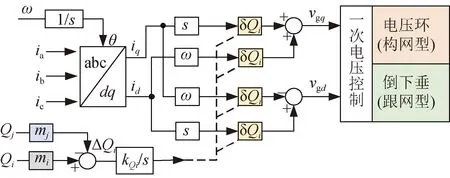
图6 自适应虚拟阻抗控制框图Fig.6 Control block diagram of adaptive virtual impedance
虚拟阻抗环节最终生成的电压矫正项如式(15)所示,补偿至GFM逆变器的一次电压环与GFL逆变器的倒下垂无功-电压控制环节。
(15)
式中:vgd与vgq为通过虚拟阻抗生成的电压矫正项;id与iq为逆变器输出电流的dq轴分量。
由于GFM逆变器需提供电压幅值支撑,故基于式(2)增加电压恢复控制:
(16)
式中:v为电压恢复项;kv为电压恢复项积分系数。
3.3 无功偏差积分系数对无功功率收敛过程的影响
上述虚拟阻抗控制中,无功偏差积分系数kQi会影响无功功率的收敛特性,需在一定范围内选取以权衡系统阻尼与响应速率。因此本部分重点分析kQi对逆变器系统无功功率收敛过程的影响。
以GFM与GFL逆变器各1台为例,自适应虚拟阻抗产生的虚拟电感值可表示为:
(17)
式中:Lvir为虚拟电感。
对本地逆变器而言,相邻逆变器经通信输送的无功信息可视为参考值,此时式(17)的小信号模型为:
(18)
虚拟电感等效补偿至线路阻抗处,如图5(a)所示,此时无功功率可表示为:
(19)
式中:VB、VB*分别为图5(a)中DG1虚拟阻抗两端电压幅值;θ为电压相角;φ为电流相角;ω为角频率。
忽略电流电压环等动态过程,式(19)的小信号模型为:
(20)
式中:Q20、Lvir0为无功功率与虚拟电感稳态值。计及无功-电压下垂(倒下垂)控制中的一阶低通滤波器,联立式(18)—(20)可得系统简化传递框图,如图7所示。

图7 系统简化传递框图Fig.7 Simplified transform block diagram of system
图7对应的传递函数为:
(21)
对于式(21)所示二阶系统,其阻尼系数与自然振荡频率可表示为:
(22)
式中:ωn与ζ分别为系统自然振荡频率与阻尼系数。
由式(22)可得:ωn随kQ2增大而增大,此时系统响应速率增加,但阻尼系数ζ变小,响应速率与阻尼系数变化趋势相反,因此实际运行中应兼顾两者折中取值,对于具体微网系统该系数的选取方法详见4.1节。
4 仿真验证
为了验证本文所提出的自适应虚拟阻抗策略可行性,在MATLAB/Simulink中搭建含GFM与GFL逆变器各1台的微网系统仿真模型,其中DG1为GFM逆变器,DG2为GFL逆变器,如无说明则逆变器容量比均为1。系统仿真参数如表2所示,仿真案例如表3所示。负荷2参数为6 000 W +3 000 var,后续负荷3参数为3 000 W+6 000 var。
4.1 无功偏差积分系数选取方法
为保证后续案例中无功输出稳定且响应速率良好,需先确定无功偏差积分系数kQi的取值范围并选取合适值[37-38]。图8为5种不同kQi值下对应的无功功率曲线收敛过程,当kQi=0.003 5时曲线模态为过阻尼,无功功率在3 s左右稳定;随着kQi逐渐增大至0.020 0,无功功率曲线逐步过渡至欠阻尼模态,输出曲线在2.5 s左右趋于稳定。
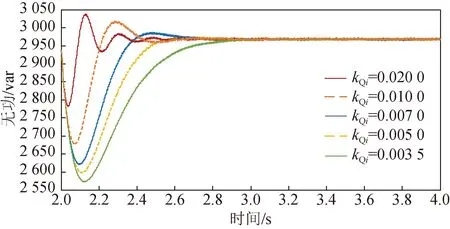
图8 不同kQi下无功功率收敛过程Fig.8 Reactive power convergence process of different kQi
随着kQi的增大,系统响应速率增加但阻尼随之下降,此时系统稳定性变差。因此综合考虑kQi取值区间为[0.002,0.100],后续案例研究中如无说明均取kQi为0.005。
4.2 案例1:对比未采用自适应虚拟阻抗
为直观且准确比较采用本文提出的自适应虚拟阻抗控制策略前后对于GFL与GFM逆变器间无功功率均分与电压恢复效果,定义无功功率偏差率nQ与电压偏差率nV如下所示:
(23)
(24)
式中:N为DG数量,偏差率越小表明无功功率均分效果越好,平均电压越接近于标幺值。
设定2台逆变器容量为1∶1,仅线路阻抗不等,具体参数如表1所示。此时仅接入负荷1。
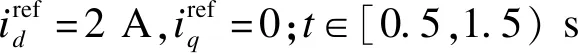

图9 未采用与采用自适应虚拟阻抗仿真结果Fig.9 Simulative waveforms of proposed strategy without and with application
对图9所得结果分析如下:
1)从图9(a)可以看出,在1.5 s前由于线路阻抗不匹配导致逆变器存在无功功率偏差,DG1与DG2分别为2 843 var与3 027 var,偏差率为3.23%;2.0 s后完全采用所提策略,稳定时DG1与DG2无功功率分别为2 869 var与2 868 var,此时偏差率为0.18%,相比于采用所提策略前明显减小。
2)从图9(b)可以看出,有功功率不受线路阻抗影响,在2.0 s完全采用所提策略后稳态时DG1与DG2有功功率相等。
3)从图9(c)可以看出,在2.0 s完全采用所提策略后,GFL逆变器电压由0.986 pu恢复至0.995 pu,GFM逆变器电压则由0.995 pu恢复至标幺值。相比于采取所提策略前,电压偏差率由1.15%降低至0.25%。
分别改变DG1与DG2线路电感为4 mH与1 mH,仿真结果如图10所示。从图10(a)可以看出,随着线路电感不匹配度加重,采用所提策略前后无功偏差率分别为13.15%与1.14%;从图10(b)可以看出,有功功率最终实现均分;从图10(c)可以看出,此时GFM与GFL逆变器电压分别由0.991 pu与0.986 pu恢复至1.00 pu与0.990 pu,电压偏差率相应由1.1%降低至0.5%。与文献[10]中采用的常值虚拟阻抗法相比,本文所提策略无需预知阻抗值,可自适应线路阻抗变化实现功率均分与电压恢复。
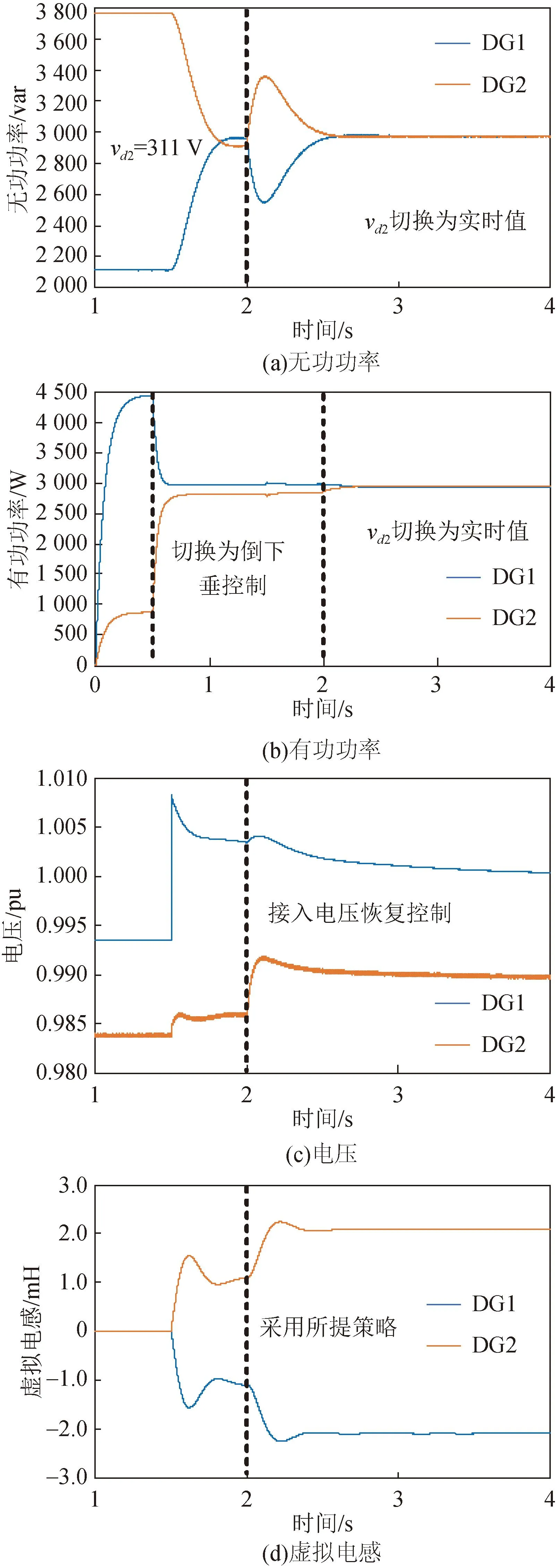
图10 线路电感变化后输出无功与电压Fig.10 Reactive power and voltage with line inductance changing
从图9(d)可以看出,DG2与DG1的自适应虚拟电感在2.5 s趋于稳态值±1 mH;从图10(d)可以看出,DG2与DG1虚拟电感稳态值为±2.15 mH,补偿后等效线路电感并不相等。其原因在于GFL逆变器电压仅基于GFM逆变器电压支撑而未受控,因此其稳态值与GFM逆变器输出电压稳态值存在偏差,使得补偿后电感不等但仍可实现无功分配。由于图10对应场景下线路电感偏差较图9增加,因此DG1与DG2输出电压偏差与等效线路阻抗偏差亦增加。
上述两种情形下负荷节点(VPCC)电压幅值如图11所示。从图11(a)可以看出,未采用所提策略前负荷节点电压为0.950 pu,t=2.0 s采用所提策略后随着逆变器输出电压幅值恢复至标幺值,负荷节点电压亦恢复至0.960 pu;从图10(b)可以看出,未采用所提策略前负荷节点电压为0.960 pu,t=2.0 s采用所提策略后恢复至0.965 pu,因此逆变器输出侧电压幅值的恢复亦有利于负荷节点电压幅值的改善。

图11 案例1未采用与采用所提策略时VPCC波形Fig.11 Load voltage amplitude of Case1 without and with proposed strategy
由于所提策略主要通过控制逆变器输出端电压实现幅值恢复而并未对负荷侧电压进行控制,故负荷节点电压未恢复到标幺值附近,但仍然在供电电压偏差所规定的标称值±7%(0.93~1.07 pu)范围内。
设定GFM与GFL逆变器容量比为2∶1且令GFL逆变器倒下垂系数增加一倍,其余参数同表1与表2,此时功率输出曲线如图12所示。从图12(a)可以看出,在1.5 s前系统无功偏差率为22.96%,2.0 s应用虚拟阻抗策略后降低为4.92%,因此所提策略适用于容量不等的情形。
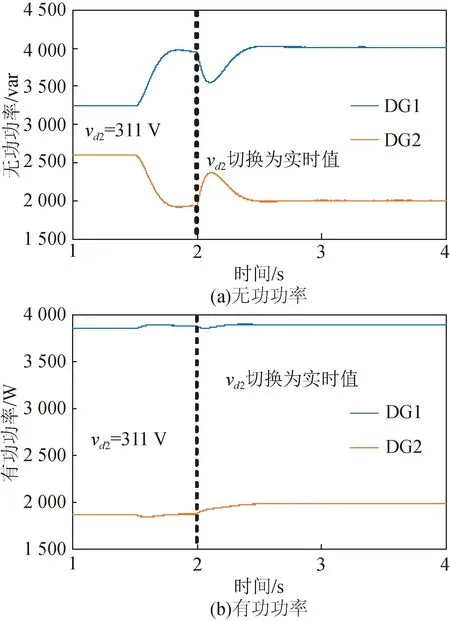
图12 逆变器容量不等下输出功率Fig.12 Power of different inverter capacity
案例1采用所提策略前后无功功率与电压偏差率如表4所示。由表4可知所提策略可改善无功功率分配并实现电压恢复。

表4 采用所提策略前后无功功率与电压偏差率Table 4 Reactive power and voltage deviation of Case1 without and with proposed strategy
4.3 案例2:负荷投切
孤岛微网中常有负载投切,因此需验证所提策略不受负荷波动的影响。负荷投入场景设定如下:t∈[0,4.5) s时微网带负载1运行,在4.5 s时接入负荷2;负荷切除场景设定如下:t∈[0,4) s时微网带负荷1与2运行,在4.0 s时切除负荷2,无功功率如图13所示。
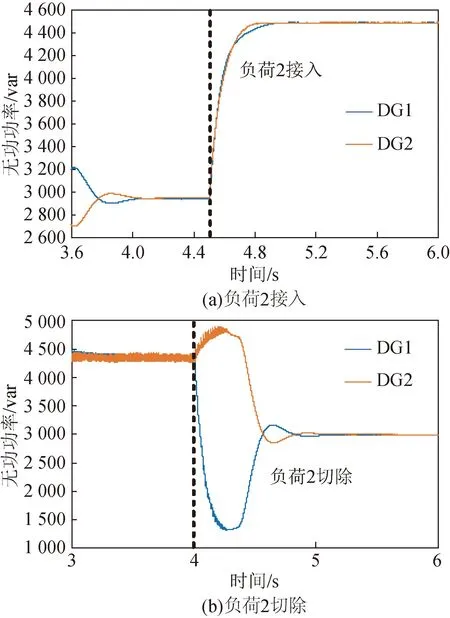
图13 负荷投切下无功功率Fig.13 Reactive power of load switching
从图13(a)可以看出,负荷2投入后0.3 s无功功率实现均分;从图13(b)可以看出,负荷2切除后1.0 s实现无功功率均分。因此在实际中发生负荷突增或突减扰动时,GFL逆变器可按照剩余容量与GFM逆变器按比例增发相应无功。
4.4 案例3:即插即用
该场景是为模拟现实中DG从微网中断开或接入的需求。设t∈[0,3.00] s微网包含DG1,DG2与DG3(GFM型)3个逆变器,其中DG3线路电感为2 mH,其余参数同DG1,1.50 s采用本文所提控制策略。t=3.00 s时切除DG3,无功功率曲线如图14(a)所示。

图14 切除与接入DG3无功功率Fig.14 Reactive power of DG3 been disconnected and connected
从图14(a)可以看出,在约1.80 s时3个逆变器系统实现无功功率均分;t=3.00 s切除DG3后约0.30 s无功功率重新实现均分。
在接入DG3前需通过预同步控制环节使其角频率,电压幅值和相位与微网一致,尽力减小电流冲击保证逆变器稳定并网[39-40],所得无功功率曲线如图14(b)所示。在t=1.0 s时启动预同步环节使角频率与DG1一致,t=2.35 s将DG3接入系统并采用所提策略。从图14(b)可以看出,当t=1.80 s时DG1与DG2实现无功功率均分,2.35 s时接入DG3,约0.40 s后重新实现无功功率均分。最终验证所提策略适用于即插即用情形。
综上所述,所提策略可适用于输电线路阻抗不等且变化、逆变器容量不等、投切负荷以及即插即用场景。
5 结 论
本文提出一种基于自适应虚拟阻抗且适用于GFM与GFL逆变器主导微网系统的无功功率分配控制策略,可实现GFM与GFL逆变器间无功功率均分与电压恢复。具体如下:
1) 采用倒下垂控制可使GFL逆变器具备无功功率下垂特性从而能够参与功率二次调节,且所提控制策略可使异构逆变器间无功功率均分与电压恢复不受输电线路阻抗影响,MATLAB/Simulink仿真结果也表明该策略在逆变器容量不等、负荷投切与即插即用下仍具备适用性。
2) 无功偏差积分系数会影响无功功率的收敛过程,其值越大无功曲线响应速率越快,但系统阻尼随之减小,应综合考虑折中选取。
本文考虑GFL逆变器参与二次功率控制时未计及剩余容量,基于此种约束的优化无功功率分配策略是后续研究的重点。

