基于路段交通量的交通需求量优化研究

赵晓晓ZHAO Xiao-xiao

（江苏建筑职业技术学院，徐州 221116）

1 动态交通需求数据优化理论基础

对交通需求数据进行优化的目的是为了弥补原始计算数据数据量上的不足，这是典型的离线动态交通需求数据反推问题，即已知研究时间范围内的历史交通需求数据（论文采用的为基于RFID 设备计算的交通需求OD 矩阵）、线圈采集的路段交通量数据、动态交通分配矩阵数据等，利用准确度较高的路段交通量数据对历史数据进行有目的的修正。

Cascetta[1]在文中对“基于路段交通量的动态交通需求数据估计问题”（绝大部分离线动态交通需求数据反推问题都包含在文献[1]的研究范畴内）做了详细的描述，并给出了如下两种一般性估计方程：

①同时估计方程（Simultaneous Estimators）。

同时估计方程“同时”的含义为：此方程可以同时估计所有研究时段的动态交通需求矩阵。

②序列估计方程（Sequential Estimators）。

序列估计方程“序列”的含义为：每次只估计一个时段的交通需求矩阵，每估计出一个交通需求矩阵，该估计值便赋值给对应时段的先验值，再继续估计下一个时段的交通需求矩阵。几乎所有的静态估计模型可以包含在这个内容下[2]。

几乎所有的离线动态交通需求反推模型都可以建模成上述两个方程的形式。

2 交通需求数据优化模型构建

任何优化问题在建模前都要先分析清楚待优化数据的特点和优化目标，本文的待优化数据为基于RFID 设备计算的动态交通需求数据，其特点为：①有与实际情况相符的变化趋势；②与对应的线圈检测交通量在数据量上有较大差距；优化目标为：在保持数据变化趋势的基础上，尽可能缩小与线圈检测交通量之间的差距。

Spiess（1990）[3]在文章中提出了静态交通需求反推方法和柯西梯度（Cauchy gradient）算法，模型如下：

观察Spiess 的模型，可以发现该模型本质上属于GLS模型的特殊一类，标准交通需求矩阵反推GLS 模型的目标函数包含两项：①待估计交通出行量与历史交通出行量之间带权重的最小二乘项；②待估计交通出行量分配到路段上的路段交通量与线圈检测路段交通量之间带权重的最小二乘项。而Spiess 只包含项目②，其含义为：给予交通量检测数据最高的可信度，权重取1，而给予历史交通需求数据最小的置信度，权重取0，这种目标模型很适用于以下两种情况：①没有历史交通需求数据的情况；②有历史交通需求数据，但是年代相隔久远，单论数据量上的参考价值不大。而RFID 计算的交通需求数据的情况与情况②大同小异，故基于RFID 计算数据的交通需求优化问题的目标函数可以参考公式（4）的形态。

初步确定优化模型的目标函数形态后，再来分析建模所需的约束条件。首先观察Spiess 方法的约束条件，条件中除了式（5）之外，只包含dij≥0 这个条件，这样泛泛的约束条件带来的弊端是：得出的最优解仅符合式（4）的目标函数，而与历史交通出行量趋势和形态相差甚远，这不符合既定的优化目标。另外，在很多研究中发现，历史交通出行量在大小趋势上往往与当前实际情况有很大的一致性，故Spiess 方法的约束条件并不合适本论文的情况。

2005 年，Doblas[4]在文章中提出以下几个静态交通需求反推问题的约束条件：

其中：lr和ur分别为起讫点对r 之间出行量的上下限；li0和ui0分别为以i 为起点的起讫点对出行量之和的上下限；ljD和ujD分别为以j 为终点的起讫点对出行量之和的上下限；l 和u 分别为路网中所有起讫点对之间出行量之和的上下限；其他未解释字母的含义同上。

观察Doblas 给出的约束条件形式，其给各交通出行量的取值、相同起点交通出行量和的取值、相同终点交通出行量和的取值、总出行量和的取值设定了一定的范围，这样的约束避免了求出的最优解与实际情况偏离太大的情况。Doblas 表示，这些范围的设定取决于规划者的判断，且具体情况具体分析，范围的设定并非一成不变。作者通过对RFID 采集数据的精度进行演算，得到本研究中比例稳定在1.1～2.6 之间，平均1.9 附近，这种范围的稳定性表明约束条件（8）是可以用于本研究的。

至此，结合Cascetta 离线动态交通需求反推问题一般方程（1）的形式，动态交通需求矩阵优化模型可建模如下：

式中，t 为每天待优化的交通需求矩阵时段，t=1，2，…，nt；

h 为优化所需的路段交通量对应的时段，h=p’，p’+1，…，nt；

dt和dt*分别为t 时段所有起讫点对r 出行量组成的列向量的实际值和优化值，向量长度为nod；

l 和u 为比例因子，根据实际情况（本研究主要考虑采集设备的特点和精度等）决定。

观察所建立的模型，目标函数（4）可以保证当把优化后的动态交通需求矩阵分配到路网上后，得到的路段交通量与实际线圈采集的路段交通量之间的差距最小；约束条件（13）限定了优化值的搜索范围，且范围的限定考虑了采集数据的实际情况，避免因优化范围太宽泛导致优化值与计算的动态交通需求矩阵在趋势上偏离过大。综上，此模型的建模思想是符合计算数据的自身特点和优化目标的。

3 算法设计

论文选取遗传算法进行优化模型的计算，其求解流程设计如图1 所示。

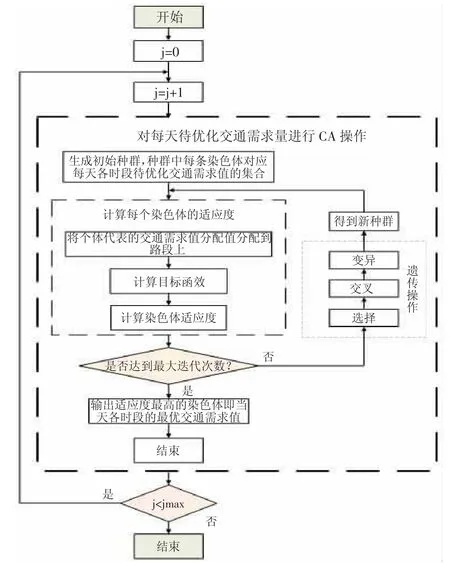
图1 GA 流程图

4 实例分析

4.1 数据描述

4.1.1 RFID 采集的过车数据

南京市作为目前RFID 基站设置密度最高的城市，拥有1300 多个基站，可以有效覆盖论文研究区域，故选取RFID 作为过车数据的采集设备。研究路网及路网内RFID基站布置情况见图2，路网包含珠江路、后宰门街、北安门街、清溪路、明故宫路、中山东路、御道街、瑞金路、黄埔路、解放路、解放南路等的部分路段。考虑研究目的，选取路网进出口路段上的RFID 基站采集过车数据。另外，经过人工调查发现，4 位置的出口路段和5 位置的出口路段交通量很小，这里在不影响研究效果的情况下对其进行省略处理，RFID 基站采集原始数据实例见表1。

表1 RFID 基站采集原始数据实例

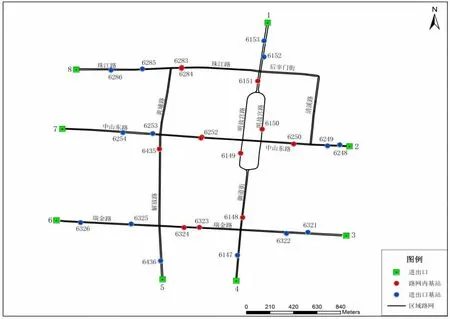
图2 研究路网及路网内RFID 基站位置

4.1.2 RFID 计算的交通需求原始数据

基于RFID 数据的交通需求量矩阵和交通分配矩阵的计算方法和实例可参见作者的前作论文[5][6]。

4.1.3 路段交通量数据

使用线圈检测数据作为研究所需的路段交通量数据，根据研究目的，设定路段交通量的采集位置和采集的时间范围与过车数据采集情况相一致，且为了简化表达，线圈编号采用相同位置的基站编号，设定线圈检测器汇集度为20min，得到的数据采集情况如表2。

表2 20min 汇集度线圈检测器采集数据实例

4.2 优化计算

4.2.1 模型和算法的参数设置

①模型参数。（表3）

表3 优化模型参数表

②算法参数。

经过多次试算，确定解决本论文模型的最优参数如表4。

表4 GA 优化算法参数表

4.2.2 优化结果

①以XX 年4 月8 日的早高峰7：00-7：20 时段为例，给出交通需求量矩阵的优化结果如表5。

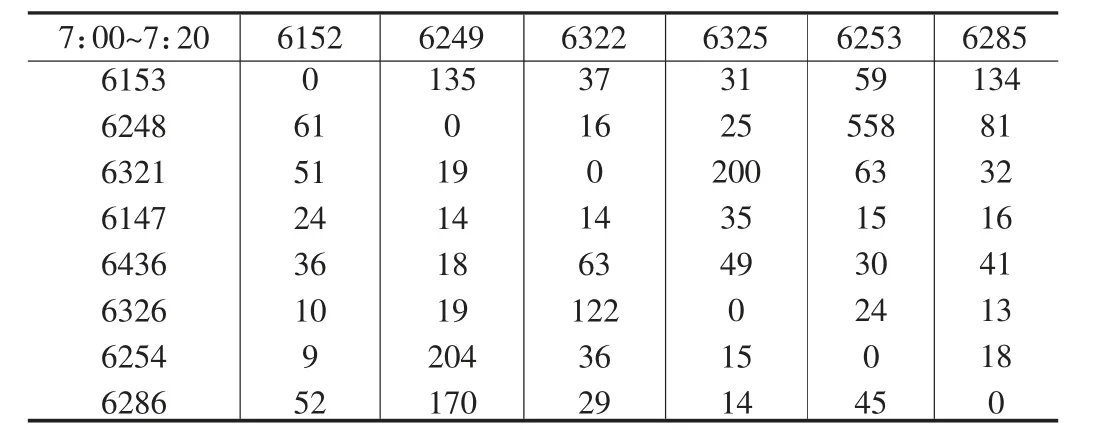
表5 XX 年4 月8 日7：00～7：20 交通需求矩阵优化终值

②该天目标函数最小值和均值的GA 收敛过程如图3。

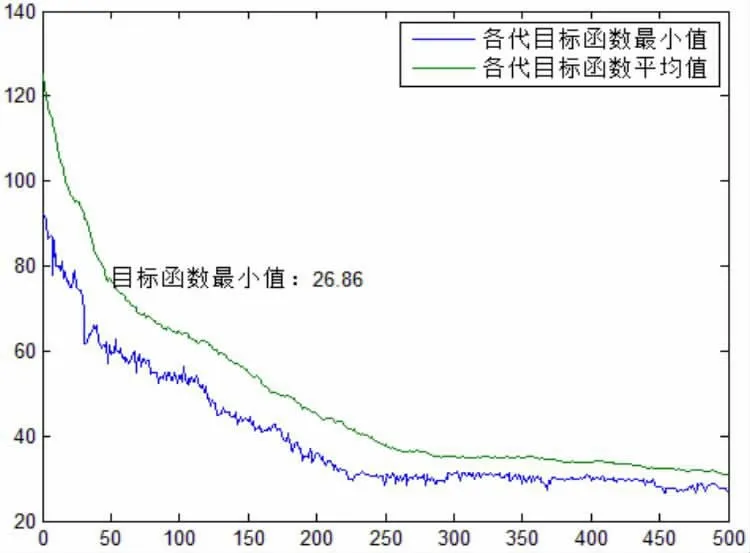
图3 XX 年4 月8 日目标函数值（适应度）收敛过程

GA 操作结束后，目标函数值为26.86，其现实含义为：将优化后交通需求量分配到路段上，与线圈检测路段交通量平均相差26.86，相当于只占检测路段交通量平均值的6%左右（XX 年4 月8 日各时段目标路段的线圈检测路段交通量均值为429），差距很小，表明优化后的交通出行量分配到路段上与实际情况十分接近。

③以XX 年4 月8 日的早高峰7：00-7：20 时段为例，交通出行量优化前后的对比图如图4。

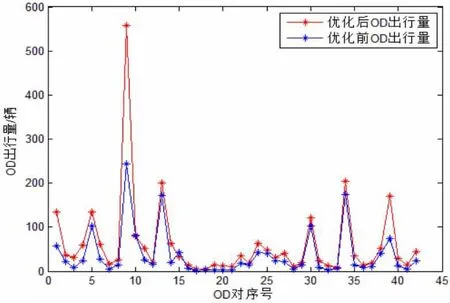
图4 XX 年4 月8 日7：00-7：20 优化前后交通需求量对比图

4.3 优化结果分析

4.3.1 相关系数检验

对优化前后的交通出行量按照如公式（14）进行相关系数检验：

其中，di*为优化后的交通需求出行量；d*为优化后交通需求出行量均值；为RFID 计算的交通需求OD 出行量；为RFID 计算的交通出行量均值。其它未解释字母含义同上。

XX 年4 月8 日早高峰6 个时段相关系数的均值求得为0.9397，证明优化前后的交通出行量高度相关，两者具有一致的变化趋势。

4.3.2 扩大效果评价

给出优化前后交通出行量与进口路段交通量关系表，进而评价模型和算法在弥补RFID 数据量不足上的效果，见表6。

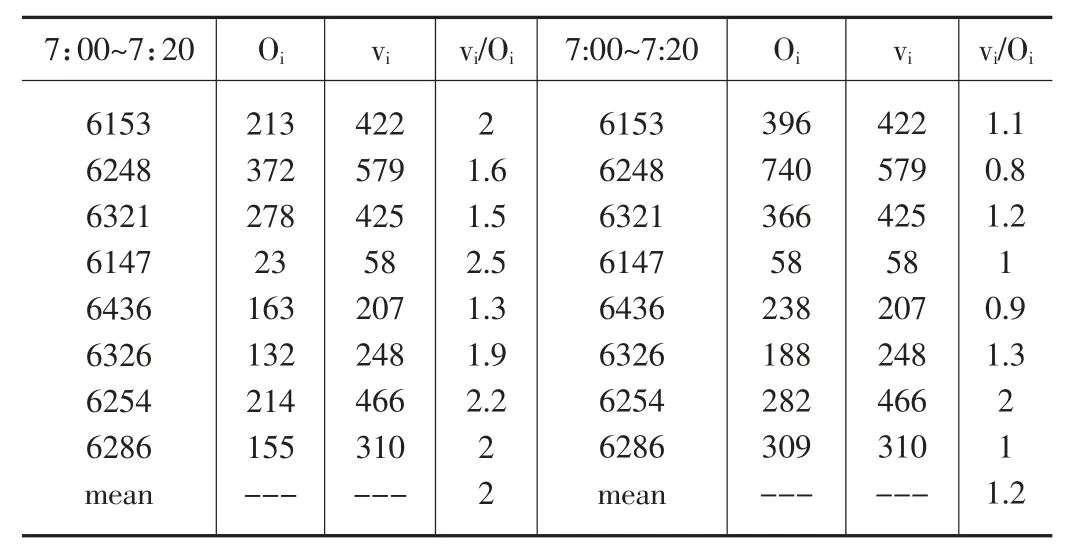
表6 XX 年4 月8 日优化前后Opi 与vip 关系表（选取7：00-7：20 时段展示）

从表6 可以发现，优化后的oi已与vi之间的差距不大，平均比值为1.2，较优化前的比值2 有了明显改善。这说明优化模型和算法在改善RFID 计算的交通需求量矩阵上有不错的效果。优化后的交通需求量可作为动态交通需求矩阵预测的历史（先验）数据，为交通状态判别、预警分析等技术提供数据支撑。