突变负载下考虑最小损耗的IPMSM滑模转速控制

张 正,李 鑫,李彩红,王传玺

(长安大学 工程机械学院,陕西 西安 710064)

0 引言

随着控制技术和材料性能的提升,IPMSM因其体积小、性能优良,被广泛应用于诸如机器人、电动汽车和数控机床等领域。虽然IPMSM具备良好的动态和静态性能,但其在工作过程中会受到外界干扰输入的影响,因此其在实际应用中的性能表现直接取决于控制策略能否处理干扰输入。研究一种能考虑外界干扰影响的控制策略是具有重要意义的。同时,负荷的变化,特别是短时过载时,会导致电流峰值大幅增加。电流在定子绕组上产生的损耗不断产生热量,其所引起的温度上升可能导致永磁体退磁。因此将损耗控制纳入控制策略的考虑中也是有必要的。

目前,针对负载突变的研究可分为自抗扰控制和滑模控制。如使用负载观测器加自抗扰控制实现对变化转矩的抗扰控制[1]。使用滑模速度控制器进行对突变转矩的抗扰控制[2-3]。针对损耗控制的研究可分为最小损耗控制[4-5]和最大转矩电流比[6]。MTPA只能实现对于定子铜耗的最小化,而没有考虑到铁芯损耗。最小损耗控制可以同时考虑铜耗和铁损的最小化,适用于需要最大效率运行的场合。因此本文以考虑铁损的永磁同步电机模型为基础,进行突变负载条件下的最小损耗和转速控制策略研究。

1 考虑铁损的永磁同步电机模型

IPMSM的损耗可分为铜损、铁损、摩擦损耗和其他杂散损耗。铜损是电流在线圈中流动产生的热损耗。铁损产生于IPMSM内部磁场的变化过程,主要为电磁效应损失。摩擦损耗为轴承等旋转部件产生的,风冷电机中的风磨损耗在本文水冷电机模型中不予考虑。其他杂散损耗是其余除上述损耗种类之外的损耗。传统永磁同步电机模型考虑的损耗只有定子电阻产生的铜损。考虑铁损的永磁同步电机模型相比传统永磁同步电机模型增加了一个损耗通路,使用铁损电阻的形式等效铁损,如图1。其中铁损电阻是通过实验测试[7]获得,将铁损电阻和转速进行插值,即可获得铁损电阻关于转速的变化曲线。

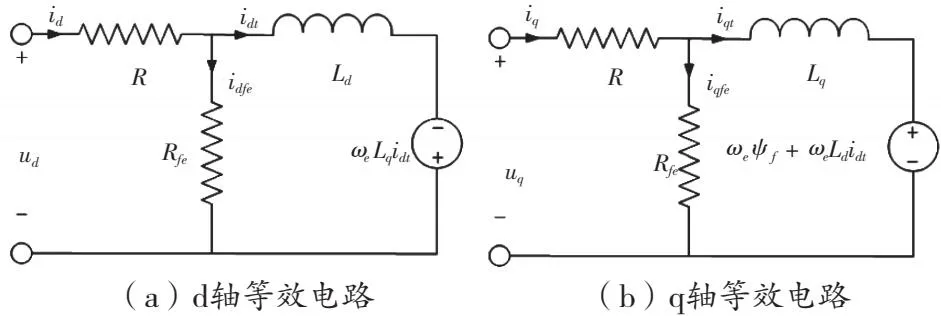
图1 PMSM等效电路

图2 PMSM控制模型

等效电路中的电流方程为:

(1)

式中,id、iq-定子电流;idt、iqt-有效电流;idfe、iqfe-铁损电流;Rfe-铁损电阻;Ld、Lq-电感;ωe-电角速度;ψf-永磁体磁链。

定子电压方程为:

(2)

将电流方程带入电压方程中可得:

(3)

PMSM的电磁转矩方程为:

(4)

式中,Te-电磁转矩;pn-转子磁极极对数。

PMSM的运动方程为:

(5)

式中,ωm-角速度;J-转动惯量;B-阻尼系数;Tm-负载转矩。

2 滑模控制器设计

2.1 新型可变边界层厚度指数趋近律

滑模控制中常用的指数趋近律为:

(6)

当系统状态s距离所设计的滑模面距离较远时,上述趋近律符号函数项和指数项同时作用,推动系统状态以一个较大的趋近速率向着滑模面靠近;随着系统状态逐渐运动到距离滑模面较近的距离时,符号函数项会占主要作用,积分项逐渐减小。趋近时间很大程度上由k1决定,增大k1可缩短趋近时间,但同时会放大抖振;减小系数可削弱抖振但会提高趋近时间,这使得常用的符号函数趋近率难以兼顾抖振和趋近时间。可用的处理方法包括将符号函数替换为饱和函数sat(s)。由于饱和函数在边界层内为一线性函数,其相比于符号函数的不断切换,可以在一定程度上抑制抖振,但作用比较有限。

使用新型指数趋近律如下[8]:

(7)

式中,k>0,k2>0,δ>0,1<ε<2,x1为系统状态变量。函数f(s)表达式为:

(8)

式中,Δ为边界层厚度。

分析上述趋近律,当s远离滑模面时,e-δ|s|趋于零,一个较大的K值使得s快速趋近滑模面。当s趋近滑模面时,e-δ|s|趋于1,此时状态变量x1一般会趋近于零,K值也随之趋近于零,使得系统抖振逐渐削弱。

此外边界层厚度也会影响抖振大小和趋近速度,因此引用可变边界层控制,使得s与滑模面距离小于ec时,自动切换到更小的边界层[9]。可变边界层厚度可描述为:

Δ=(1-α)Δ1+αΔ2

(9)

当距离大于ec时,α=1;当距离小于等于ec时,α=0。

(10)

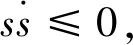
2.2 滑模控制器设计

传统速度控制多采用PI速度控制,其难以满足如IPMSM这种复杂模型的抗干扰性能和动态性能要求。滑模控制的抵抗外部扰动干扰能力强且响应速度快,因此设计滑模控制器实现转速的强抗扰控制。由于本文后续采用最小损耗控制,d轴参考电流不是id=0,而变为id=idfe,其中idfe为最小损耗电流,转速控制模型为:

(11)

定义PMSM系统的状态变量:

(12)

在单个控制周期内,可将Tm和idfe视为恒定值,根据式(11)和式(12)可推导得:

(13)

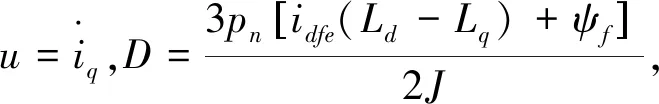
(14)

定义滑模面函数为:

s=cx1+x2

(15)

式中,c>0,为待设计参数,对s求导得:

一辆2014款上汽通用雪佛兰爱唯欧Aveo ，搭载1.4L直列4缸发动机和5速手动变速器，行驶里程为30 943km，因发动机故障灯常亮而送修。

(16)

采用指数趋近律的控制器得表达式为:

(17)

则q轴参考电流为:

(18)

2.3 负载观测器设计

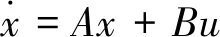
(19)

(20)

2.4 最小损耗控制

前述的损耗之中,杂散损耗和摩擦损耗是不可控的,因此不考虑这两者的控制。铜耗和铁耗则可以通过定子电流使其产生一定幅度的变化。因此最小损耗控制即是在满足负载要求的前提下调节定子电流使铜耗和铁耗组成的总损耗最小。总损耗计算公式为:

Ploss=Pcu+Pfe

(21)

在离散控制系统内进行损耗计算时,出于简化问题的考虑,认为电流在一个控制周期内是一个稳定值。因此去掉微分项,并将iqt使用转矩方程进行变换。IPMSM在实际工作中的idt电流幅值不大,且交直轴电感相差也不大,可以对损耗公式继续简化,可得:

Ploss=

(22)

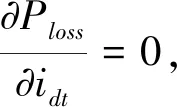
(23)

3 系统仿真

依据前述考虑铁损的IPMSM数学模型在Simulink中搭建电机的仿真模型。模型使用两电平逆变器为电机供电,转速环采用滑模控制器,电流环采用PI控制器,d轴电流参考值由最小损耗控制模块给出。电机的额定转速为3000 rpm,额定功率为30 kW,额定转矩为100 N/m,冷却方式为水冷,永磁体布置方式为内置式。电机内部参数Pn=4,Ld=0.2236 mH,Lq=0.4975 mH,R=15.7 mΩ,Ψf=75.98 Wb,J=0.018015 kg·m2,B=0.00017 N·ms。为比较分析本文控制策略的性能,将本文基于新型趋近律设计且结合龙伯格负载观测器的滑模控制器(NSMC+LDO)与传统PI和传统控制律滑模控制(SMC)进行对比分析。新型趋近律滑模控制器参数为k2=25,k=90,δ=1.2,ε=1.5,边界层厚度Δ1=10,Δ2=25;传统趋近律滑模控制器参数c=20,q=240,ε=90;PI速度控制器参数P=200,I=40;电流环参数为P=0.2,I=5。

以额定转速3000 rpm为目标转速,并在0.2 s处施加100 Nm的突变转矩,并在0.4 s处撤去负载转矩,采用三种不同控制策略的转速仿真波形如图3所示。在空载启动时,三种控制策略均在达到目标转速时产生了转速波动。其中,NSMC与LDO结合的控制策略的上升时间为0.046 s,调节时间为0.053 s,超调量为0.26%;SMC的上升时间为0.046 s,调节时间为0.063 s,超调量为0.32%;PI的上升时间为0.043 s,调节时间为0.057 s,超调量为0.44%。空载启动下的LDO不对NSMC做输出补偿,因此其上升时间与普通SMC基本一致。而新型可变边界层厚度趋近律的存在,使NSMC能够比普通SMC以更小的抖振和更短的调节时间达到目标转速值。PI控制因其大增益和积分环节的存在,以3 ms左右的差距先于滑模策略到达目标转速的90%界限,但其转速波动和超调量均比滑模策略要更大。在突加转矩时,NSMC与LDO结合的控制策略的最大转速跌落值为29 rpm,调节时间为5.2 ms左右;SMC的最大转速跌落值为36 rpm,调节时间为9.8 ms左右;PI的最大转速跌落值为37 rpm,调节时间为46.8 ms左右。LDO将负载转矩的观测值补偿至NSMC的输出中,大大加快了转速的响应速度,并减小了转速波动大小。在突然减载时,三种控制策略的最大波动转速分别为7.4 rpm、9.4 rpm、18 rpm,调节时间分别为5.4 ms、9.5 ms、8.1ms。SMC因抖振的存在,其调节时间较长。分析可得,NSMC与LDO结合的控制策略在响应速度、抗抖振性能和抗干扰能力上均比SMC和PI优良。

图3 转速响应图

图4(a)所示从上至下分别为NSMC+LDO控制、SMC控制及PI控制时,转矩的响应曲线。通过对比可以发现,NSMC与LDO结合的控制策略具有转矩响应快、超调幅度小的优点。图4(b)所示为LDO负载观测器的观测值变化曲线,分析可知其响应时间大约为4 ms,响应速度较快。

图4 转矩响应及观测图

图5从上至下分别采用最小损耗控制和采用id=0控制的总损耗变化曲线。空载时,最小损耗控制的损耗约为75 W,id=0控制的损耗约为165 W;额定转矩下,最小损耗控制的损耗约为1011 W,id=0控制的损耗约为1105 W。由于最小损耗控制的id不为零,内置式电机因交直轴电感不完全相等会额外增加部分转矩,其能使电机的动态性能得到部分提升。从图中亦可发现,最小损耗控制的调节时间比id=0时的快8 ms左右,这也导致其有更大的转速超调。因此最小损耗控制在转速发生变化的损耗会更高一些。

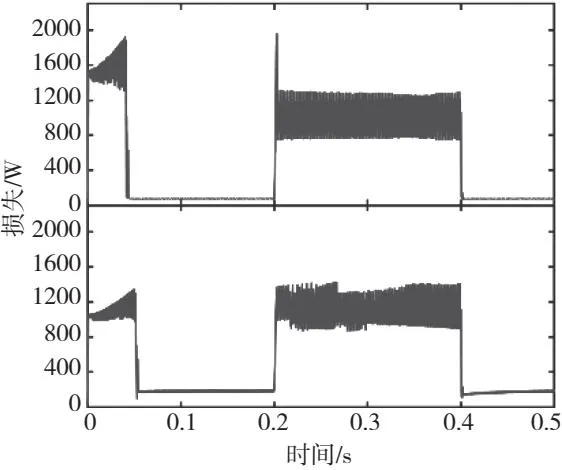
图5 损耗变化图

4 结论

本文选择考虑铁损的内置式永磁同步电机作为研究对象,并对其在同步旋转坐标系中建模,然后依据新型可变边界层厚度指数趋近律设计滑模速度控制器,并以d轴最小损耗电流为参考进行最小损耗控制。设计具有大增益的龙伯格观测器,将转矩观测值前馈补偿到控制输出中,提高控制器对于突变转矩的抗扰能力。将本文设计的控制策略与传统滑模和PI控制进行对比,结果表明,NSMC+LDO控制具有更好的抗抖振性能和较强的抗干扰能力,在应对突变转矩时更加稳定。相比id=0控制,最小损耗控制有效降低了稳态损耗。