基于刚柔耦合仿真的地铁车焊接构架疲劳分析*

王帅钧,方 吉▲,马 亮,王耀亭

(1.大连交通大学机车车辆工程学院,辽宁 大连 116028;2.包头铁道职业技术学院,内蒙古 包头 014060)

0 引言

由于城轨车有着载客量大、运营班次频繁的特点,所以其运行安全性一直备受关注。焊接构架作为城轨车最重要的承载部件之一,在城轨车运行过程中承受和传递车体和轮对之间各种复杂交变载荷作用,其线路运营条件下的疲劳问题日益突出。国内外诸多学者在焊接结构疲劳寿命评估方面取得了一定的成果,例如JW.Han等人[1]通过全尺寸台架疲劳试验对城市磁悬浮列车转向架构架进行了疲劳寿命分析。KW.Jeon等人[2]基于JIS-E-4207标准,采用Goodman-Smith曲线对转向架构架的疲劳强度进行了评估。Cera.A等人[3]结合了Apinis.R关于复合材料高频应力疲劳测试的研究成果[4],对轨道车辆常见的焊接结构形式进行了研究。孙守光教授等人[5]以高速列车在京沪客运专线上的准静态载荷-时间历程数据所创建的载荷谱为基础,对焊接构架疲劳寿命进行了理论计算。杨广学教授等人[6]提出了一种基于随机可测的等效应力幅值来对高速列车焊接构架进行疲劳寿命评估的新方法,该方法相比于其他方法更具有针对性。

本论文以某地铁车动力学性能及转向架构架疲劳寿命为研究对象,基于刚柔耦合动力学模型及实际运行线路统计数据,参照GB/T5599—2019等标准对该地铁车动力学性能进行评价。为了较准确地考虑到焊缝局部应力集中及结构振动对疲劳寿命的影响,建立地铁车整车刚柔耦合动力学模型,考虑到该城轨车复杂的线路运行条件,为了更好地模拟该车全寿命周期的运营工况,本文将结合城轨车实际运行线路统计数据,编制对应线路工况,进行动力学仿真分析,基于动力学仿真结果引入模态结构应力法对该车的焊接构架进行疲劳寿命评估与分析,并对结构进行改进方案分析与研究。

1 焊接构架柔性体模型的建立

根据该地铁车的转向架构架的几何模型,采用壳单元对结构进行离散建立到有限元模型中,如图1所示,其中焊缝局部细节如图2所示。在轴箱弹簧座、空气弹簧座、减振器安装座、纵向牵引拉杆座等位置,设置柔性体的外部接口。采用改进后的Craig-Bampton模态综合法进行求解,部分低阶柔性体模态如表1所示。

表1 柔性体部分低阶模态

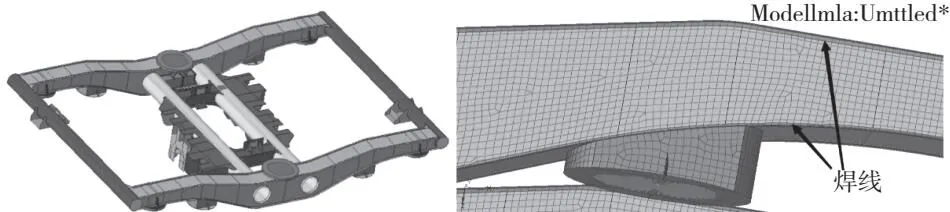
图1 城轨车转向架图2 转向架构架焊缝细节有限元模型

构架模态分析的目的是为了得到构架在受影响的频率范围中所对应的模态特性,预测构架在特定频率范围内激振源的作用下导致的响应历程或响应谱,它是结构故障诊断和动态设计必不可少的条件,防止构架发生共振和自激振荡造成事故[7]。

从上述固有频率表及固有振型图中可以得到以下模态分析结果:

(1)该城轨车转向架构架第7阶振型频率值为40.63 Hz,振型为构架整体扭曲变形,构架的最大变形发生在构架前后两端横梁与侧梁接角位置,这表明该转向架构架有一定的轮轨垂向不平顺适应能力。

(2)该城轨车转向架构架的第8阶到第10阶的自振频率分别为72.54 Hz、72.93 Hz、84.41 Hz。振型主要为前后两端横梁的弯曲及剪切变形,最大变形位置也主要集中在前后两端横梁上,这表明该转向架构架有一定的横向弯曲刚度。

(3)该城轨车转向架构架的第11阶和第12阶自振频率较大,均为100 Hz以上,振型主要为横梁及侧梁的横向、垂向弯曲,最大变形位置主要集中在构架中间的四根横梁上。这表明该转向架构架有一定的垂向、横向刚度。

在刚柔耦合转向架系统中,构架为柔性体,其他构件如轮对、轴箱、Z型牵引拉杆等都为刚体。柔性体的模态主要由约束模态和界面主模态经过二次坐标变换而来,该综合模态既能有效地拟合结构的准静态变形同时又能较好地拟合结构的振动形变[8]。本次柔性体的制作借助 ANSYS软件与ADAMS之间的接口来完成。约束模态取40阶,界面主模态96阶(16个接口,每个接口6自由度,每个自由度对应一阶界面主模态)。具体制作流程如图3所示。

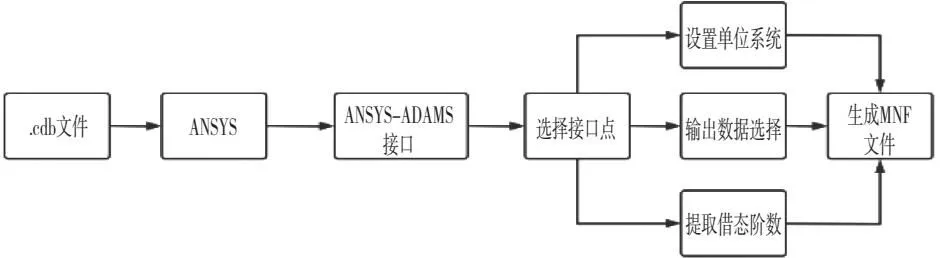
图3 构架有限元模型柔性化流程图

2 刚柔耦合模型的建立

在刚柔耦合模型中,柔性体与刚体通过动力学方程(1)来建立耦合联系。

(1)

其中,广义坐标ξ包括:模态坐标q、位移坐标x以及欧拉角坐标ω;广义力通过Q表达;L是拉格朗日函数;λ为待定因子;ψ(ξ,t)为完整约束方程。

地铁车整车动力学模型由车体和前、后两个转向架三个子系统组成,其中转向架构架为柔性体,其余除弹性元件外均为刚体模型。该地铁车动力学模型子系统结构图如图4所示。

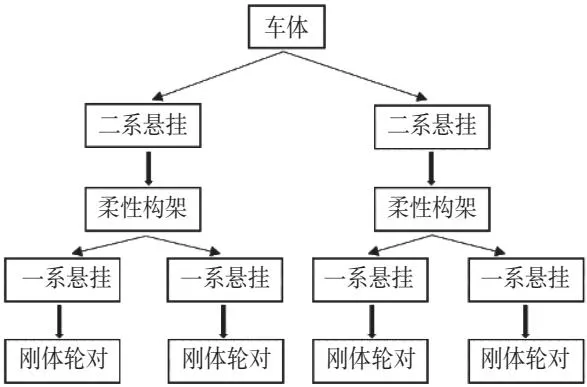
图4 城轨车子系统结构图

转向架是地铁车最重要的部件之一,主要起缓冲与减振作用,转向架刚柔耦合模型如图5所示。

图5 城轨车刚柔耦合转向架动力学模型

在车体子系统以及前后转向架子系统都建立完成之后,我们便可以在ADAMS/Rail的标准模块中对城轨车整车动力学仿真系统进行装配。本次计算以某地铁车头车基本参数进行建模,车体简化为刚体,车体与转向架构架之间通过空气弹簧、牵引拉杆、抗侧滚扭杆等子结构进行连接。装配完成后的城轨刚柔耦合动力学模型如图6所示。

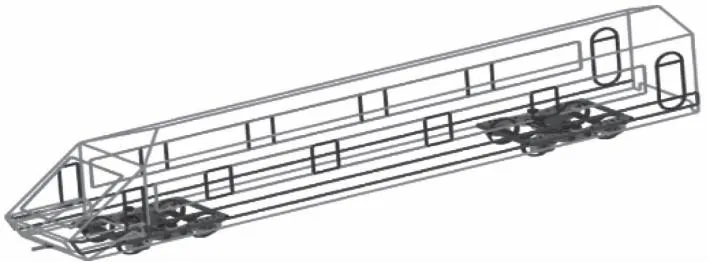
图6 地铁车刚柔耦合整车动力学模型

3 线路运行工况的模拟

本次计算以轨道不平顺为激振源,直线、曲线线路均施加美国五级轨道不平顺谱进行仿真。由于该车设计最高时速为120 km/h,而实际运营速度以100～60 km/h为主,所以分别设置120 km/h、100 km/h、80 km/h、60 km/h四种速度工况进行仿真分析。首先对车体的振动加速度进行分析并对舒适性进行评价(图7-图11),然后分析了运行速度对脱轨系数及减载率的影响(图12、图13)。结果显示:随着列车速度的提高,舒适性降低,且均小于2.5,属于优级别,随着城轨车速度的提升,脱轨系数也随之增大,且均满足标准要求。

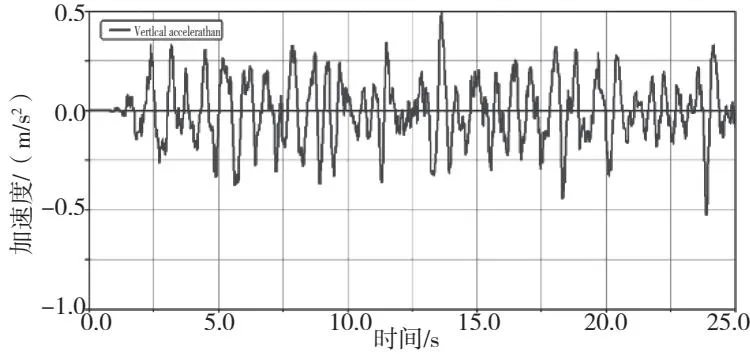
图7 车体垂向振动加速度时间历程(120 km/h)

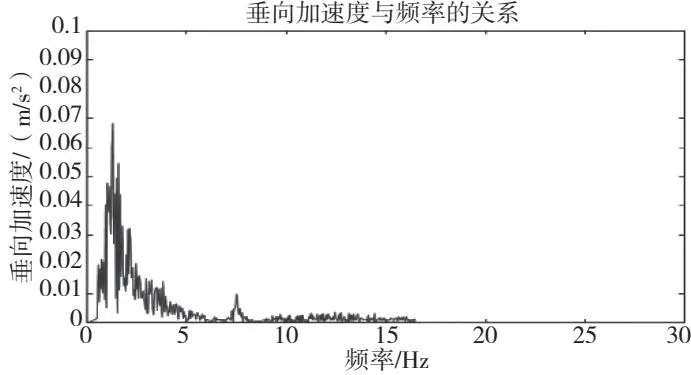
图8 车体垂向振动加速度幅频图(120 km/h)

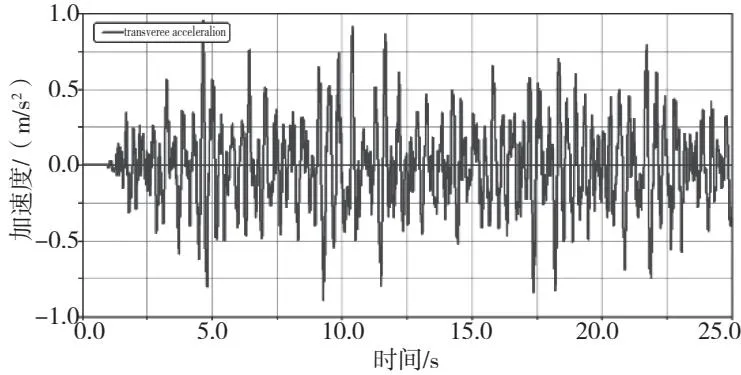
图9 车体横向振动加速度时间历程(120 km/h)

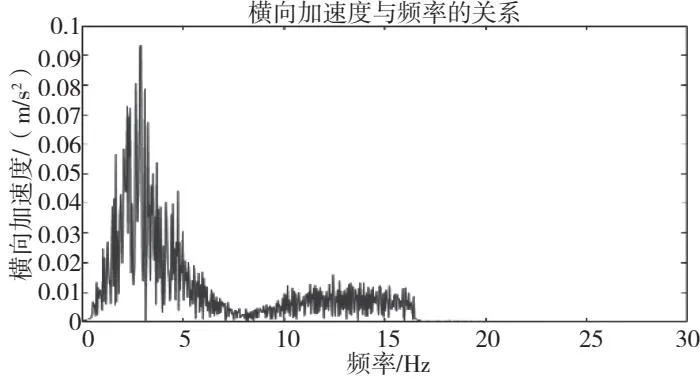
图10 车体横向振动加速度幅频图(120 km/h)

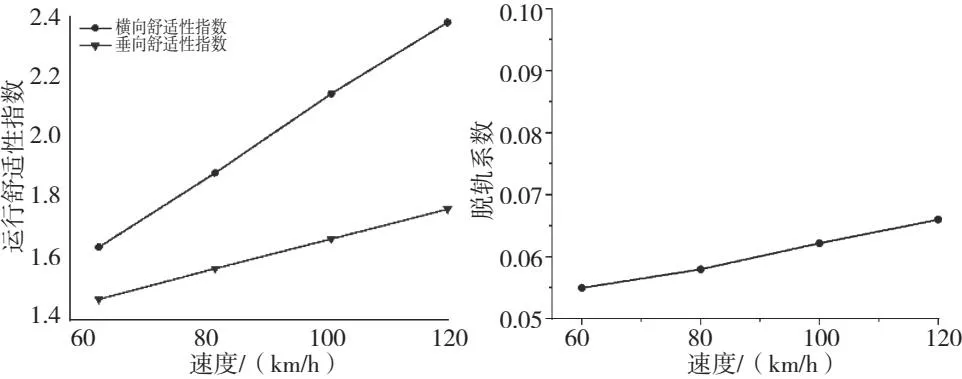
图11 舒适性评价图12 脱轨系数趋势图

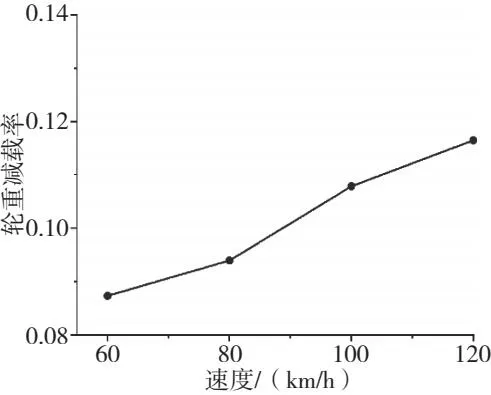
图13 轮重减载率趋势图

4 关键焊缝疲劳分析

4.1 模态结构应力法

模态结构应力法是在网格不敏感结构应力法与模态综合法的基础上提出的[8],可以适用于基于刚柔耦合时域动力学仿真结果的焊缝振动疲劳评估,其主要实施流程如图14所示。

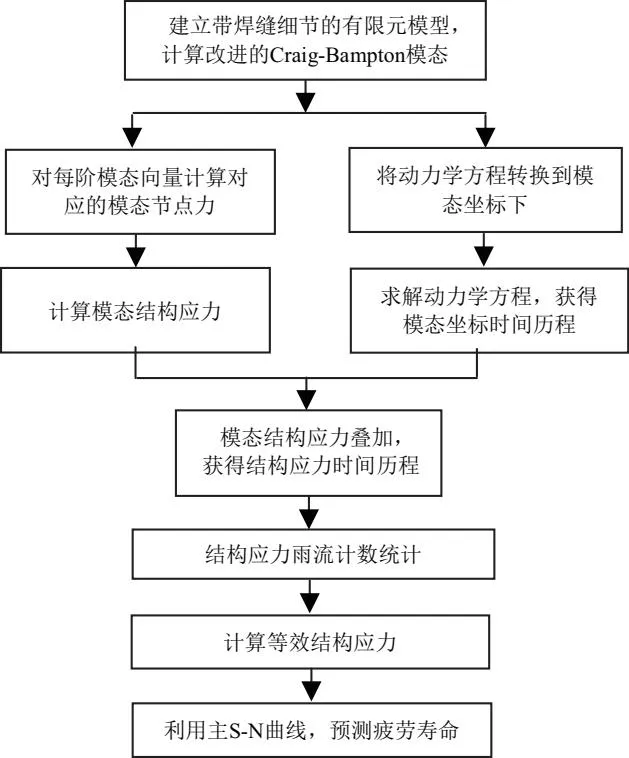
图14 基于模态结构应力法的疲劳寿命预测流程

4.2 关键焊缝的定义

由于该焊接结构的焊缝比较多,且均成对称分布,为了减少数据量,从中选取了8条具有代表性的关键焊线(图15)进行疲劳评估。

图15 关键焊缝定义

4.3 焊缝疲劳评估

基于动力学仿真获得的柔性体模态坐标时间历程,采用模态结构应力法求解来获得焊缝上焊趾处等效结构应力,如图16所示,图17则为等效结构应力雨流计数结果。

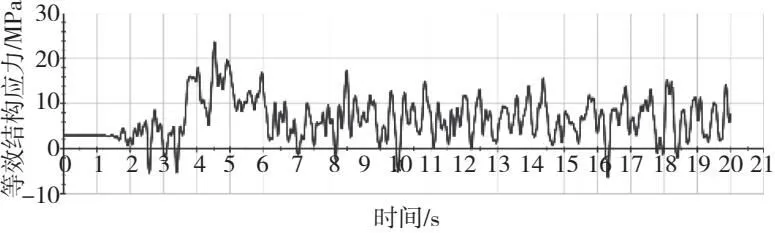
图16 等效结构应力时间历程(曲线R280)

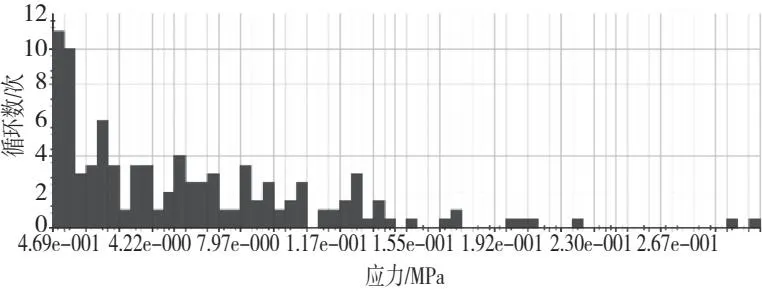
图17 等效结构应力雨流计数(曲线R280)

将各个工况计算获得的损伤按线路占比进行损伤累加,通过折算获得总寿命里程(表2)。

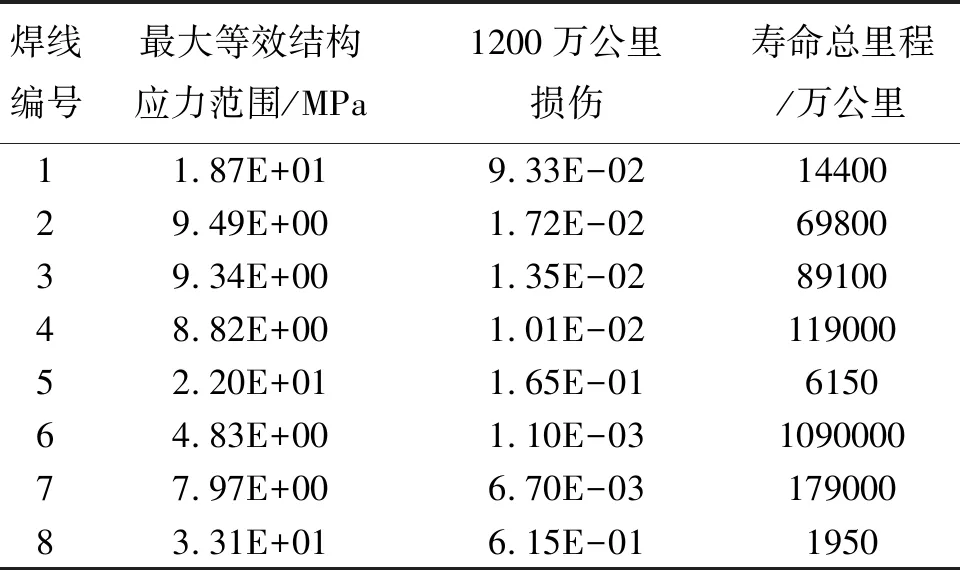
表2 构架关键焊缝疲劳评估结果

根据表2可以看出,各焊缝的疲劳寿命均满足1200万公里的要求,但是由于焊接结构抗疲劳特性的离散型,一般需要留有一定安全余量,一般要求累计损伤小于0.5,而焊缝8的抗疲劳能力未达到要求。因此需要针对该焊缝的局部结构进行优化,从而提高焊缝疲劳寿命。

5 结构改进分析

由于该地铁车的线路以曲线为主,列车通过曲线时速度较快,而空气弹簧的横向刚度比较小,因此车体产生的横向位移较大,横向止档座承受一定载荷作用,导致其焊缝寿命降低。提高焊缝抗疲劳性能主要有以下几个途径:1)焊缝位置避开应力集中;2)缓解焊缝局部应力集中; 3)降低焊缝结构承受的载荷。将安装座改成其他连接方式,结构改动太大,成本会提高;延长止档座筋板的长度可以达到缓解应力集中的效果,基于此提出了改进方案(图18)。

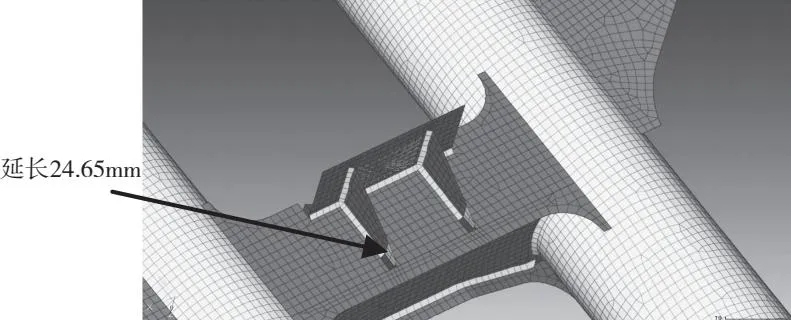
图18 焊缝8局部改进方案

按照上述改进方案,基于相同的方法进行仿真计算并给出疲劳损伤评估对比曲线,如图19所示,可以看出构架横向止档座处关键焊缝的改进方案能有效提高焊缝抗疲劳能力。

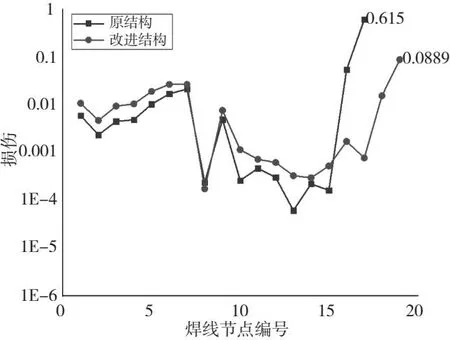
图19 焊缝8改进前后损伤对比

6 结论

本文以某地铁车转向架构架的疲劳寿命为研究对象,首先建立刚柔耦合动力学模型对地铁车的动力学性能进行评估;然后,采用模态结构应力法对构架进行了疲劳寿命分析;最后,根据疲劳分析结果,对构架关键焊缝进行结构改进。通过本次研究,得出如下结论:

(1)动力学仿真分析结构显示:该车动力学性能各项指标均满足GB/T5599—2019要求。

(2)由于该地铁车的运营线路以曲线为主,且通过曲线时速度较快,而空气弹簧的横向刚度比较小,因此车体产生的横向位移较大,横向止档座承受一定载荷作用,导致其焊缝寿命降低。

(3)构架横向止档座处关键焊缝的改进方案能使得焊缝局部刚度更协调,从而减小焊缝局部应力集中,有效提高焊缝抗疲劳能力,且结构改变小、实施方便,说明焊接结构设计过程中,保障焊缝局部的刚度协调非常重要。