大口径真空蝶阀阀体非线性稳定性分析

杨繁隆,冯万平,陆 欢

(江南阀门有限公司,浙江 温州 325013)

0 引言

结构的刚度、强度和稳定性是衡量产品性能优劣的重要指标[1],其中,刚度和强度是阀门行业评估产品结构性能的主要依据,而失稳作为结构失效的一种重要形式[2],少有企业涉及。是指当载荷超过结构内部的抵抗力时,结构失去原有几何形状的现象,即:外载荷即使有微量扰动,结构变形亦有显著变化的趋势[3]。

大口径真空蝶阀[4],安装在内部压力低于大气压的蒸汽管道系统中,是抽真空系统的关键主件。为保证真空蝶阀在负压工况下工作性能,在确保阀体刚度、强度符合要求的基础上,应避免阀体出现失稳现象。本文,以我司自产的DN1600真空蝶阀阀体为研究载体,采用特征屈曲法和弧长法,借助有限元软体,确定失稳临界载荷值,为企业在大口径真空阀门稳定性分析提供方法参考和理论依据。

1 结构稳定性有限元法

1.1 稳定性

结构稳定性是结构在外载荷作用下,外力和内力保持平衡的状态。衡量结构是否稳定的标志是确定结构失稳的临界点,当外载荷达到临界值,即使后续少有微小扰动出现,结构就会出现不断增加的永久变形。目前,常用的稳定性有限元分析方法包括:特征值屈曲法和非线性屈曲法[5],前者是基于结构弹性理论的线性计算,材料始终处于弹性行为,得到的临界值远超真实数值,无法应用于实际工程分析;后者,以材料处于屈服阶段为基础,增加模型初始缺陷和扰动等参数,得到贴合实际的屈服力[6]。

1.2 弧长法

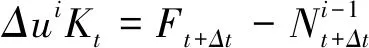
弧长法作为目前常用的非线性屈曲分析法,可以通过选取适合的极值点使得求解结果收敛。该方法的优点是对结构非线性分析中高效可靠的迭代控制[7],有效地分析非线性前后屈曲并在追踪结构加载路径、确定临界值上具有独特优势。

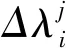
图1 弧长法迭代求解曲线

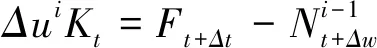
2 阀体非线性稳定性分析

2.1 真空阀阀体模型和主要性能参数

目前大口径真空蝶阀阀体多采用卷板焊接的形式:中间为阀体筒体,两侧为上下法兰筒体,阀体外圆焊以加强筋和圈筋增强阀体刚度。本次分析,以蝶阀阀体为主要载体,视焊接件为整体,对各部件重新建模得到单一零部件,去除边角等影响,得到数学模型如图2所示。

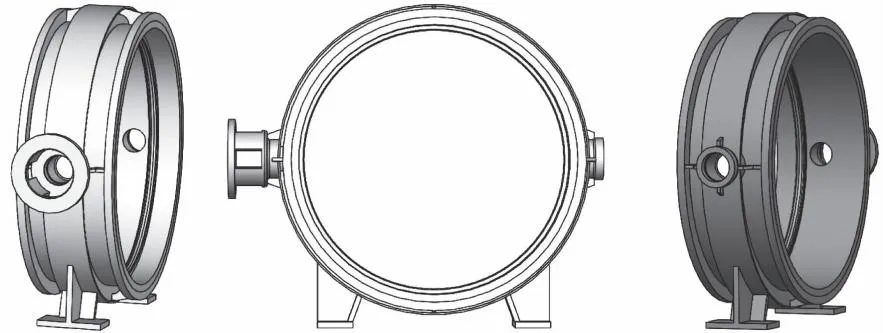
图2 三维模型

阀体材质以Q345R[8]为主,其力学参数及真空蝶阀性能参数如表1所示。

2.2 前屈曲分析

本次稳定性分析分为前屈曲分析和后屈曲分析两阶段,前者即线性特征值屈曲,是求解理想载荷系数的前提,以小位移线弹性理论为基础,辅以刚度矩阵|Ke|和应力矩阵|Kσ|求解任意阶的特征值,(Ke+λiKσ)vi=0为第i阶的平衡方程。特征值表征载荷系数,其与单位载荷的乘积即为临界载荷值,此数值相对于实际工况过于保守,但其可以作为后屈曲分析阶段的初始载荷使用。

本文使用Solidworks Simulation[9]屈曲分析模块,阀体地脚与进口段为固定端约束、出口段为径向约束,载荷为0.1 MPa负压;采用整体网格划分方式:单元数29312个,节点数51192个;求解器选用软弹簧模式,前6阶特征值数值分别为:29.152、30.237、35.553、35.843、40.425和44.051。本次分析选取第3阶特征值作为理想系数,按上述方法所述,得到后屈曲分析载荷值为-4.5 MPa。

2.3 后屈曲分析

后屈曲分析,是基于弧长法求解失稳临界值的非线性有限元法。本文认为,失稳“非线性”的体现应主要包括如下两方面内容。

首先,材料应符合非线性要求,应力应变值达到弹性阶段临界点后可自行进入屈服阶段。为便于计算且利于结果的收敛性,本文采用双线性本构方程来模拟材料屈服行为,第一阶段线性曲线的切斜率为弹性模量E的函数,第二阶段线性曲线的切斜率为切模量G的函数。

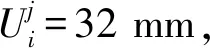
非线性屈曲分析仍采用与特征值屈曲相同的数学模型、网格结构和约束条件,材料为双线性参数形式,外载荷为-4.5 MPa。为进一步确保求解收敛,设置收敛公差ε=10E-4。

求解完成后,需选取某一节点或某一部件作为对象,得到其响应载荷因子和位移的关系曲线。本次分析,阀体以零部件形式出现,因此,得到某一节点的因子-位移曲线,即可得到真空蝶阀阀体的临界载荷因子。选择第3阶段特征屈曲分析中,特征振幅值最大的节点作为参考对象,该节点编号为12622,如图4所示。

图4 第3阶特征屈曲节点最大值

2.4 结果分析

得到节点12622的位移-载荷因子曲线,如图5所示。通过观察,将曲线分为两个阶段,第一阶段A-B:载荷因子相比于施加于阀体的位移扰动比率极大,斜率为1.55左右,此阶段阀体材料仍处在弹性阶段;第二阶段B-C:载荷因子相比于施加于阀体的位移扰动比率极小,斜率为8.9E-3左右,此阶段阀体材料进入屈服阶段,但始终没有超过材料的屈服极限值。位移呈现不断增大的情况,说明阀体在B-C段已经出现失稳现象,B点(5,1.55)即为临界失稳点,此处的载荷因子λs=1.55,即为临界载荷因子。

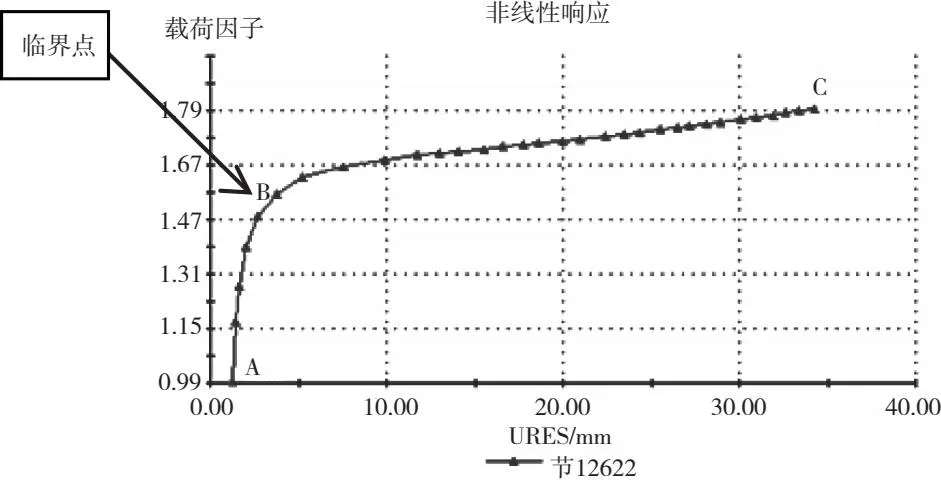
图5 位移-载荷因子曲线

本次分析初始载荷为4.5 MPa负压,临界载荷因子为1.55,得到最终的临界载荷为6.975 MPa的负压,该数值远大于阀门最大压差-1.5 bar的要求,因此,该真空阀阀体在最大负压工况下不会出现失稳现象,满足长期服役的稳定性要求。

3 结论

(1)对DN1600真空阀阀体进行非线性稳定性分析,得到失稳临界点坐标为(5,1.55),发生失稳的临界载荷为-6.975 MPa,满足实际工况要求。

(2)本文以真空蝶阀阀体为载体,借助双线性材料曲线、施加微小位移扰动,采用基于弧长法的非线性有限元分析方法,较特征值法得到更贴合实际的数据,为今后阀门企业在稳定性分析方面提供了理论依据和方法支撑。