基于负载观测的开关磁阻电机线性自抗扰控制*

贲 彤,张永超,陈 龙,b,井立兵

(三峡大学 a.电气与新能源学院;b.湖北省输电线路工程技术研究中心,宜昌 443002)

0 引言

开关磁阻电机作为一种新型的电机,因其结构简单、成本低、易于维护等优点在工业领域得到了广泛应用[1-3]。然而,SRM的非线性、耦合、时变等特性对其控制带来了很大挑战。传统的PI控制易实现,能满足大多数场景的应用,但面对外部负载变化导致的干扰时,难以满足高精度控制需求[4-5]。近年来,针对SRM的控制技术研究成为了研究的热点,以提高其控制性能和抗干扰能力[6-7]。

为了增强SRM控制系统的抗扰动能力,国内外学者提出了众多方案。韩京清[8]提出了自抗扰控制(ADRC),是PI控制的替代方案,广泛应用于电机控制中抑制速度超调和速度波动,但是其参数过多,直接影响到控制器的精度和应用;GAO等[9]基于ADRC理论,提出了线性ADRC控制器,减少了可调参数;章玮等[10]设计了降价负载观测器观测负载,并将负载转矩引入到电流控制器输入,对PI调节器做补偿;LI等[11]提出一种直接自适应神经网络控制器,该控制器考虑了参数变化、外部负载扰动和输入饱和约束,但其控制效果取决于神经网络的训练质量;HE等[12]将改进的自抗扰控制应用于无刷直流电动机,增加谐波注入方案,有效地减小了系统的转矩脉动,然而自抗扰控制的控制效果依赖于ESO的观测精度,当负载变化较大时,观测精度会受到较大扰动的影响。

针对负载扰动变化对SRM控制系统的影响,本文提出了基于负载观测的线性自抗扰控制(LADRC-L)方法。设计负载观测器可以提高负载扰动的观测精度,分担LESO的观测负担。同时,将观测到的负载转矩进行转换,对LADRC的输出进行补偿,提高了SRM控制系统的抗干扰能力,减小了负载变化引起的转速偏移。最后通过仿真实验,证明了本文提出方法的有效性。

1 SRM运动数学模型

SRM的数学模型是一个非线性、多变量的系统。由基本的电路定律可以得到第k相绕组的电压平衡方程为:

(1)

式中:Uk为第k相绕组端电压,Rk为第k相绕组电阻,ik为第k相绕组电流,ψk为第k相绕组磁链,θ为转子位置角。

当SRM电磁转矩与作用在电机轴上的负载转矩不相等时,转速就会发生变化,从而产生角加速度。根据动力学原理,可以得出此时的电机转矩平衡方程式:

(2)

式中:ω=dθ/dt,Te为电磁转矩,TL为负载转矩,J为转动惯量,D为摩擦系数。

当SRM进入稳态运行时,dω/dt=0,则有:

(3)

基于以上分析,SRM的转速受到负载转矩变化的影响。为防止负载的变化对控制系统造成影响,需要对转速进行精确的控制。

2 SRM负载观测器设计

本文基于龙伯格观测器原理来设计SRM负载观测器,龙伯格观测器是以系统状态方程为基础,利用系统中的可测误差和可观测误差作为系统反馈的状态观测器。

由式(2)可得SRM速度变化率为:

(4)

由于负载转矩TL不可测量,ω可测量,根据式(4)选取TL、ω分别作为待观测量和可测变量。即状态变量x=[ωTL]T,令输出量y=[ω],输入控制变量u=[Te]。状态空间一般形式为:

(5)

式中:A、B、C为系数矩阵,结合式(4)、式(5)得到:

(6)

利用反馈控制原理,通过反馈增益矩阵L=[L1L2]T,将系统真实输出与估算值误差引入至状态空间方程,可构造出龙伯格观测器为:

(7)

将系数矩阵A、B、C和反馈增益矩阵L代入式(7),状态方程展开为:

(8)

因此,得到SRM系统的负载观测器最终形式:

(9)

式中:L1和L2是反馈增益矩阵L中的元素。

矩阵元素L1和L2的值可以根据李雅普诺夫第二定理得到。观测器的特征方程可以表示为:

(10)

式中:E是单位矩阵,λ是特征值根。设两个期望极点为p1和p2。理想观测器特征方程表示为:

λ2-(p1+p2)λ+p1p2=0

(11)

求解约束,L1和L2为:

(12)

负载转矩观测器的结构如图1所示。反馈系数可由式(12)通过配置p1和p2使观测值接近真实值得到。

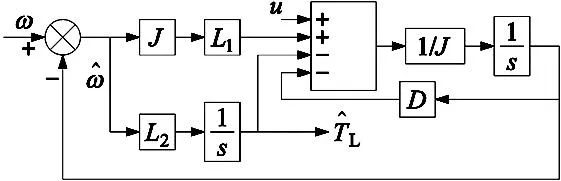
图1 负载转矩观测器的结构

3 基于负载观测的SRM自抗扰控制

根据上文分析,为了提高负载扰动的观测精度,建立了SRM负载转矩观测器。为了进一步增强SRM控制系统的抗负载扰动能力,消除转速超调,还需要设计自抗扰控制器,生成控制量。并通过转换观察到的负载转矩来补偿自抗扰控制的输出。

3.1 线性自抗扰控制器设计

将SRM系统的总扰动用f(t)表示,表示为:

(13)

式中:g(t)表示系统中未建模的未知扰动。

选取输入量u=Te,记输出量y=ω,b=1/J,由式(4)和式(13)可得到SRM速度闭环控制系统的状态方程:

(14)

根据上述公式,对于状态空间方程,可以设计二阶LESO:

(15)

式中:z1表示实际转速ω的估计,z2表示总扰动f(t)的估计,b0为输入放大系数,β1和β2为观测器的反馈增益,如果LESO的带宽为β0,可以取:

(16)

β0决定了LESO的收敛速度,一般带宽越高跟踪速度越快,但是由于噪声影响,β0的值通常是有限的。

状态误差反馈控制器设计为:

u0=KP(ωref-z1)

(17)

式中:KP表示比例系数,ωref表示参考速度。

将估计扰动z2补偿给系统可得:

(18)

基于上述方程,可得到LADRC最终形式如下:

(19)

3.2 基于负载补偿的线性自抗扰控制

式(15)中的z2是LESO估计的系统总扰动f(t),包括已知扰动和未知扰动。通过上文设计的负载观测器观测到负载转矩,分担线性自抗扰控制器中LESO的观测压力,LESO仅需观测系统内的未知扰动。因此,结合负载观测器,可以得到本文设计的LADRC最终形式为:

(20)

式中:z2被重新设计为:

(21)

此外,通过补偿因子KC将观测到的负载转矩转换为补偿值,对LADRC的输出进行补偿。将补偿后的值作为参考转矩对SRM进行直接转矩控制,其表达式为:

(22)

式中:Tref为补偿后的参考转矩。采用转矩分配函数(TSF)对SRM进行转矩滞环控制,最终的控制系统结构如图2所示。

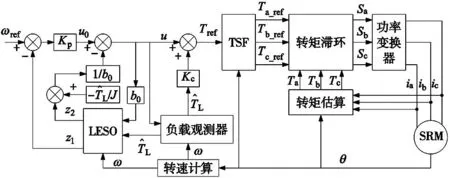
图2 LADRC-L控制系统结构

4 仿真实验与分析

基于以上理论分析,设计出了基于负载补偿的SRM线性自抗扰控制器(LADRC-L),按照控制系统总体框图如图2所示,搭建仿真模型。为验证本文提出的控制方法的有效性,对SRM速度控制系统设计仿真对比实验,分别采用经典PI控制和LADRC-L策略进行控制。

仿真的SRM参数如表1所示。

表1 SRM参数

转速超调σ和转速偏移kn定义为:

(23)

式中:nmax为转速的最大偏移量,n(∞)为稳态转速,nref为参考转速。

为验证负载观测器的有效性,给SRM施加3 N·m的初始负载,在0.2 s时变为6 N·m,0.4 s时变为4 N·m。负载转矩的观测值如图3所示。从图3可知,负载观测器的调节时间为0.03 s,稳态误差为0.02 N·m,因此该观测器动态响应快,超调量小,稳态精度高,可实时观测负载转矩。

图3 负载转矩跟踪曲线 图4 转速跟踪曲线对比

为验证转速跟随性能,设置仿真时间为0.9 s,负载为3 N·m,初始转速为500 r/min,在0.3 s时加速到1000 r/min,0.6 s时加速到1500 r/min。比较传统PI控制和LADRC-L的控制效果如图4所示。

由图4对比结果可知,在启动阶段和两次加速阶段中,传统PI控制的转速超调量σ分别为10.74%、7.73%和5.32%,LADRC-L的转速超调量均为0;传统PI控制达到稳态所用时间为0.07 s,LADRC-L仅为0.04 s。以上数据表明,LADRC-L具有更好的转速跟踪性能,能够快速无超调地跟踪转速变化。

为了验证抗负载扰动的性能,分别在500 r/min和1500 r/min的转速条件下进行仿真实验,仿真时间设置为0.9 s,初始负载为2 N·m,在0.3 s时突增为6 N·m,0.6 s时突卸为4 N·m。比较传统PI控制和LADRC-L的控制效果如图5、图6所示。

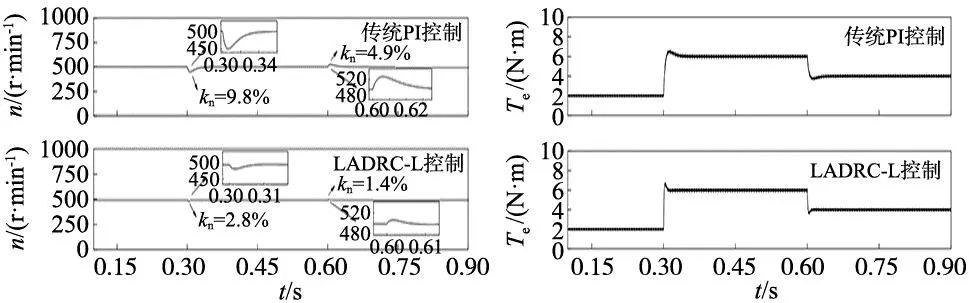
(a) 转速变化对比 (b) 输出转矩变化对比

(a) 转速变化对比 (b) 输出转矩变化对比

由图5可知,SRM在低速(500 r/min)运行时,传统PI控制在负载突变到6 N·m时,转速偏移kn为9.8%,在0.06 s后回归稳态,0.6 s时负载突卸到4 N·m,转速偏移kn为4.9%;而LADRC-L在负载突变到6 N·m时,转速偏移kn仅为2.8%,0.01 s后回归到稳态,负载突卸到4 N·m时,kn仅为1.4%。

由图6可知,SRM在高速(1500 r/min)运行时,传统PI控制在负载突变到6 N·m时,转速偏移kn为3.3%,当负载突卸到4 N·m时,转速偏移kn为1.6%;LADRC-L在负载突变到6 N·m时,转速偏移kn为0.9%,在0.01 s后迅速恢复到稳态,负载突卸到4 N·m时,kn仅为0.4%。

通过以上数据,说明在不同的转速工况下,LADRC-L抗负载扰动的性能要明显优于传统PI控制,鲁棒性强。从图5、图6可以看出,在负载发生变化时,LADRC-L的输出转矩响应速度要明显强于传统PI控制,因此LADRC-L具有更好的抗负载干扰的能力。

5 结论

针对具有负载扰动的SRM控制系统,提出了基于负载观测的线性自抗扰控制(LADRC-L)方法,减少了LESO的观测负担,并采用前馈补偿参考转矩。通过对比仿真实验得到以下结论:

(1)本文设计的SRM负载观测器能够快速、准确地跟踪负载转矩。稳态误差仅为0.02 N·m。

(2)本文提出的LADRC-L方法具有良好的转速跟踪性能,可以快速跟踪SRM的不同转速指令,跟踪速度快,无超调。

(3)本文提出的LADRC-L方法可以有效提高SRM控制系统抗负载干扰的能力。负载发生变化时,最小转速偏移仅为0.4%。且输出转矩响应更快。