基于加权最小二乘法的变保真代理模型*

韩畅阳,王 硕,刘富文,宋学官

(大连理工大学机械工程学院,大连 116024)

0 引言

代理模型是目前解决工程优化问题的有效途径,通过少量样本点构建真实系统的映射关系可以有效减少计算成本,提升设计效率[1]。然而随着设计变量和精度要求的提升,获取构建代理模型所需的样本点对于复杂系统而言面临计算成本过大的问题。对此,研究人员提出了变保真代理模型方法(multi-fidelity surrogate,MFS)[2],将样本分为高保真和低保真,高保真样本能描述物理系统的真实特征但计算成本高,低保真样本只能描述物理系统的最显著特征但计算效率高,因此需要融合两种保真度的样本建立代理模型,保证模型精度的同时平衡模型性能和建模效率的关系。值得注意的是,对于以某种方式获得的样本,无法简单判断其为高保真还是低保真[3],保真度概念是相对而言的,例如仿真数据相对于实验数据为低保真,粗网格仿真相对于细网格仿真为低保真[4]。

多保真代理模型按照建模方法可以分为3类:基于Co-Kriging的方法、基于映射的方法、基于修正函数的方法。其中基于修正函数的方法应用最为普遍[5],具体可以分为3类:乘法修正函数、加法修正函数、综合法修正函数。

乘法修正函数最早由HAFTKA[6]提出,假设高低保真度代理模型之间存在的差异为比例关系,因此通过修正因子描述相同样本处高保真和低保真响应的差异。ALEXANDROV等[7]将该理论应用到了空气动力学优化问题中,但是乘法修正函数只能较好地描述局部映射关系,当真实系统比较复杂时,该方法的精度难以达到预期;另外遇到低保真响应值趋近于0的情况时,修正因子会趋向无限大,此特性一定程度限制了其在工程领域的应用。因此,研究学者提出了加法修正函数以避免上述情况的出现。加法修正函数假设高低保真度代理模型之间存在一个偏差项,因此添加了差异函数来表达高低保真样本的偏差关系[8],该方法以其形式简单、鲁棒性强的特点被研究人员所青睐。综合修正函数结合了前两种方法的优点,进一步提升了模型准确性,被广泛应用于工程优化问题中,DURANTIN等[9]提出了一种基于径向基函数的变保真建模方法,通过留一法最小化高低保真模型的误差来优化参数,并应用到气体传感器的设计问题。SONG等[10]基于径向基函数建立变保真代理模型,并通过扩展矩阵快速计算模型系数。WANG等[11]提出了一种基于移动最小二乘法的变保真代理模型,该模型提供了一种影响域的自适应求解方案,并根据每个预测点影响域内的样本计算权重及未知系数。

受综合修正函数理论启发,本文提出了一种基于加权最小二乘法的变保真代理模型方法(MFS-WLS)。在MFS-WLS中,先使用修正因子对低保真响应进行缩放,使其与目标响应更为接近。再通过类似多项式的形式描述二者的差异关系。由于加权最小二乘法是由单项式组合形成的,因此在MFS-WLS系数求解过程中,以加权最小二乘法为基础,把修正因子和低保真响应值作为多项式的一项,将其与差异多项式构成单项式线性组合的形式,并对每个高保真训练样本分配不同的权重以增加关键样本的影响力,最后通过加权最小二乘法最小化高保真响应和MFS-WLS预测值之间的误差。

1 MFS-WLS模型

1.1 加权最小二乘法估计原理

最小二乘法的核心思想是利用已有的自变量X和因变量Y的实验数据,通过最小化误差的平方来寻找自变量和因变量之间的函数表达。一般最小二乘法解决曲线拟合问题的基础公式可表述为:

f(x)=α1φ1(x)+α2φ2(x)+…+αnφn(x)

(1)

式中:αk(k=1,2,…,n)是待定系数,φk(x)是事先选定好的一组线性无关的函数。在公式中,一般最小二乘法将不同采样数据同等对待,而在实际情况中不同采样数据重要性往往不同,因此加权最小二乘法给予了每个采样点不同的权重因素wi,构建误差平方和公式得:

(2)

对αk求偏导得:

(3)

式中:

(4)

(5)

1.2 MFS-WLS理论

在变保真代理模型的构建方法中,综合法由于结合了灵活性高和预测能力强的优势而被广泛应用,该方法的基础公式可描述为:

ye(x)=ρyc(x)+z(x)

(6)

式中:x代表设计空间中的设计变量,ye(x)代表样本x基于高保真模型的响应,yc(x)代表样本x基于低保真模型的响应,ρ为修正因子,z(x)为差异函数。综合修正法的原理是先采用修正因子对低保真响应进行缩放,然后用z(x)对缩放后的低保真数据进行校正,模型求解流程如图1所示。

图1 MFS-WLS模型求解流程图

对式(1)进行以下转化:

(7)

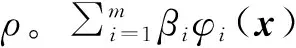
在MFS-WLS中,将缩放的低保真响应作为多项式中的首项,与差异函数集成为矩阵乘积的形式。具体的:

(8)

式中:

φ(x)=[yc(x)φ1(x)φ2(x) …φm(x)]

(9)

构建误差平方和I(β):

(10)

式中:xi(i=1,2,…,n)为高保真样本。将上述公式转换为矩阵形式:

I(β)=(φβ-ye)TW(x)(φβ-ye)

(11)

式中:

ye=[ye(x1)ye(x2) …ye(xn)]T

(12)

(13)

(14)

对式(11)求β的偏导:

φTW(x)φβ(x)=φTW(x)ye

(15)

因此:

β(x)=(φTW(x)φ)-1φTW(x)ye

(16)

根据式(11)得:

(17)

1.3 权重系数

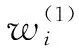
(18)

(19)

2 数值案例

本节将MFS-WLS模型与应用较广的两种变保真代理模型和一种单保真代理模型进行对比,验证其预测能力及鲁棒性。

2.1 试验设计

试验设计(design of experiment,DoE)[12]是一种结构化设计策略,通过DoE得到空间分布较为均匀的抽样点,一般抽样点越多空间填充性越好,建立的代理模型精度越高,然而抽样成本也随之升高,因此要选择合适的抽样策略,用尽量少的样本点表达整体设计空间的均匀性和填充性。目前工程中较为常用的抽样方法包括:拉丁超立方抽样(LHS)、全析因抽样(FFD)、正交抽样(OA)和中心复合抽样(CCD)等。在众多的抽样方法中,LHS作为一种分层抽样方法,因其具有产生均匀、近似随机样本的强大能力而被广泛应用,因此LHS作为本文的主要DoE方案。

由于本文将MFS与单保真和多保真两类代理模型进行比较,因此需要考虑两种保真度样本的抽样比例问题。以高保真样本表示预算抽样成本,假设总成本为5d,d为问题维度即设计变量的个数,则构建单保真代理模型时的样本个数为5d,构建变保真代理模型时,需要消耗一部分预算成本生成低保真样本,将生成高保真样本的成本和总预算成本的比值设置为θ,θ∈(0,1),将评估一个高保真样本和评估一个低保真样本的成本比值设为δ,则构建变保真代理模型时,低保真样本的个数为5δ(1-θ),具体地令δ分别取10、20、30、40、θ分别取0.8、0.6、0.4,得到如表1所示的抽样方案。

表1 抽样方案表

2.2 评价指标

代理模型描述输入变量X和输出响应Y的映射关系,作为真实系统的近似模型能够被工程实例问题采用的前提是精度符合预期要求,因此需要对MFS-WLS模型的预测性能进行评估。本文以应用最广的决定系数(coefficient of determination,R2)作为模型的评价指标。R2可以表示模型的全局预测精度,其数学表达式为:

(20)

2.3 数值测试函数

高保真函数:

ye(x)=(x1-1)2+(x1-x2)2+x2x3+0.5

(21)

低保真函数:

yc(x)=ye(x)-0.5x1-0.2x1x2-0.1

(22)

式中:x1,x2,x3∈[0,1]。

选取5d(d=3)高保真的预算成本来构建代理模型,其中80%用于产生高保真样本,剩余的20%产生低保真样本。成本比率分别设为10、20、30、40,产生不同的训练样本数量如表2所示。

表2 训练样本统计表

针对每种情况进行30次独立抽样,分别生成30组抽样点,再针对每组抽样点分别构建MFS-WLS模型、CoPRS模型、MFS-RBF模型和RBF单保真模型并计算决定系数R2,绘制R2平均值条形图(图2)、R2箱型图(图3)、MFS-WLS优于其他模型的次数统计图(图4)。

图2 模型精度均值统计图

图3 模型精度箱型图

图4 MFS-WLS优于其他模型的次数统计图

从图2中可以看出,绝大多数情况中MFS-WLS模型的平均值较其他模型更大,说明MFS-WLS模型具有更好的预测能力。图3箱型图中异常值用十字号表示,箱型图的高度(第1、3四分位数之间的距离)代表统计数据的大致范围,箱型图的高度越小,表示数据越集中鲁棒性越好,模型越稳定。反之表示鲁棒性越差。从图中可以看出,MFS-WLS模型箱型图的高度更小,因此性能更好。图4显示了MFS-WLS模型具有比其他模型精度结果更高的次数,次数最大值为30,值越大表示即使在样本分布情况不同时,MFS-WLS也具有良好的预测能力和更强的鲁棒性。例如成本比为20时,在27组样本中MFS-WLS比同组样本创建的MFS-RBF更精确,在全部30组样本中MFS-WLS均比CoPRS和RBF更精确。值得注意的是,随着成本比增大,低保真点越多,MFS-WLS模型性能表现越好,这是因为构建的低保真模型越精确,对应的修正模型也越精确。

为了进一步验证MFS-WLS的预测性能,另取10个测试函数,设置高保真样本点数为4d,成本比为20,对每个测试函数生成30组初始随机样本,依次建模并进行精度计算,最后统计模型R2的均值。结果表明,对于大部分测试函数,MFS-WLS均有更好的预测能力。

3 工程实例

压力机是机械制造领域中的一种重大装备,在汽车、轮船等制造过程中发挥着重要作用。在设计过程中,压力机横梁通常需要较高的强度和刚度以承受液压缸的推力,然而保守的经验设计经常造成质量过重,刚度冗余过大的问题,因此对压力机横梁的质量与应力的有效预测在其结构设计中具有重要意义。本节将针对压力机上梁进行轻量化设计,该上梁采用的材料为Q235-B,相关参数如表3所示。图5为模型示意图,在原有设计基础上进行优化,提取4个可优化设计变量,其中x1为肋板厚度,x2为壁板厚度,x3为上下板中线距离,x4为上盖板厚度。在保证横梁刚度前提下,通过优化横梁尺寸和形状参数,达到降低横梁重量的目的。经有限元分析,上梁的变形峰值为3.129 mm,将其作为重要约束条件;模型最大应力较小,为120 MPa,因此仅作为结果的验证条件。本节的优化问题可以写成一个标准非线性方程:

表3 横梁结构材料属性

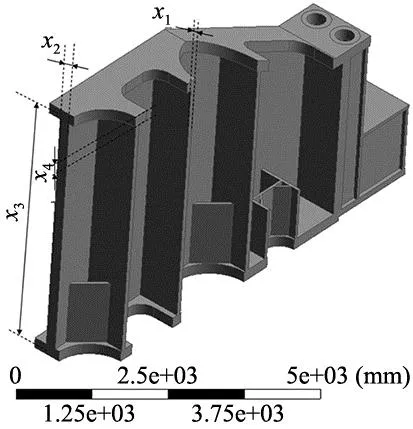
图5 上梁结构设计变量示意图

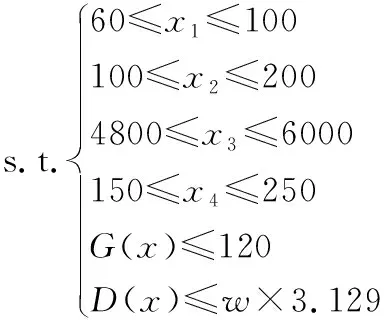
(23)

式中:x2单位为mm,M(x)为待优化上梁质量,G(x)为最大应力,D(x)为最大变形,w为最大变形系数。

本节使用网格质量作为区分有限元模型精度的指标,将网格尺寸分别设置为80 mm和55 mm,并计算不同网格质量对应的样本响应值。设置高保真点抽样成本为4d,成本比为20,本案例为4维问题,因此取16个高保真样本和20个低保真样本,分别构建质量(M)函数、变形(D)函数、应力(G)函数的变保真模型,另取20个高保真样本作为测试样本。使用MFS-WLS与前文提到的CoPRS、MFS-RBF以及RBF分别创建预测模型,并对模型的精度进行评价,计算决定系数均值,比较结果如表4所示。

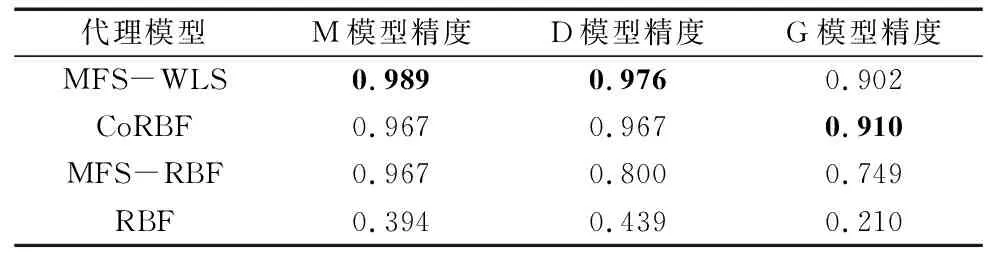
表4 模型精度比较表

由表中数据可知,MFS-WLS在构建M模型和D模型时精度更高,分别为0.989和0.976。构建G模型时精度略低于CoRBF模型,但数值相差不大。整体来看,MFS-WLS模型在实际工程问题中具有较好的预测能力。值得注意的是,单保真代理模型RBF的精度远小于另外3种变保真代理模型,由此凸显变保真代理模型在少量高保真样本情况中的强大预测能力以及开发变保真代理模型算法的必要性。

4 结论

本文提出了一种基于加权最小二乘法的变保真代理模型算法(MFS-WLS),相比于大部分变保真算法,MFS-WLS通过加权的高保真样本计算未知系数,然后利用WLS结合低保真模型和差异函数表示高保真响应。 将MFS-WLS与多个主流代理模型算法进行对比测试,在测试函数和工程实例两个方面,MFS-WLS均具有较好的预测能力和鲁棒性。此外,在总预算成本相同情况下,成本比越高MFS-WLS表现越好。

在进行工程应用之前,需要考虑问题的维度和总预算成本,尤其对于高维问题,MFS-WLS可能因为求解速度慢而表现不佳,因此在未来将继续改进模型,提升在高维问题中的计算效率和精度。