轴向力下圆锥结合面切向刚度分形模型分析*
靳 岚,李卫兵,卢世奇,曾鑫磊
(兰州理工大学机电工程学院,兰州 730050)
0 引言
圆锥连接因具有可易调整过盈量、拆卸方便和降低连接界面损伤等特点[1],广泛应用于旋转类机械装备以实现传递扭矩等工作,如高性能机床电主轴中主轴-刀柄的圆锥连接、高压辊磨机主轴与辊套的圆锥连接、船舶重载轮毂圆锥连接等。在这类圆锥连接时,由于结合面受压产生了变形,使得由结合面法向接触刚度、切向刚度组成的圆锥连接整体刚度影响着传递扭矩的有效性,其中切向刚度的强弱对工况下的圆锥连接装配体回转精度和安全性有着重要的影响。因此准确建立圆锥结合面切向刚度模型,对分析圆锥结合面的接触特性,提高圆锥连接的整体刚度尤为重要。
对于结合面切向刚度模型的建立,众多学者进行了不断地探索。陈奇等[2]建立了圆柱结合面切向刚度模型,研究了摩擦因数、分形维数、特征尺度参数、材料的特性系数等对结合面切向刚度的影响。李志涛等[3]应用改进分形理论及连续变形理论建立了切向刚度模型,发现两结合面的静摩擦力使实际接触面积增大,导致结合面刚度也增大。王世军等[4]考虑了微凸体弹塑性过渡阶段的弹性,研究结果表明,切向刚度随着法向载荷的增大而增大,随着特征尺度参数与切向载荷的增大,切向刚度减小。孙宝财等[5]根据微凸体接触变形方式,建立了滑动摩擦界面切向刚度分形模型,认为切向刚度随分形维数、真实接触面积和材料特性系数的增大而增大,切向刚度随特征尺度、摩擦系数的增大逐渐减小,但忽略了微凸体之间的相互作用。王润琼等[6]提出考虑微凸体相互作用、且引入域扩展因子可使所建结合面接触刚度分形模型更加准确。
在众多切向刚度模型研究中,很多都是建立的平面或圆柱面结合面切向刚度分形模型,很少有圆锥结合面接触刚度的相关文献。为了建立较为准确的圆锥结合面切向刚度模型,分析轴向加载过程中的圆锥结合面各参数影响切向刚度的规律,本文通过借鉴圆柱结合面接触刚度分形模型,构造了圆锥结合面接触系数λc,为建立圆锥结合面接触分形模型奠定基础;在此基础上,在考虑微凸体相互作用的前提下引入域扩展因子,构建了圆锥结合面切向刚度分形模型。最后以高性能加工中心关键部件高速主轴中的主轴-刀柄圆锥连接为研究对象,通过与实验结果的比较,验证建立的圆锥结合面切向刚度分形模型的准确性,并获得了轴向力加载过程中的分形维数D、特征尺度G、材料塑性指数φ等因素影响主轴-刀柄圆锥连接装配体结合面切向刚度的规律,为承受轴向载荷的圆锥连接设计提供了理论依据。
1 构造圆锥结合面接触系数
圆锥结合面接触系数λc主要用于修正圆锥面接触面积密度分布函数,是建立圆锥结合面切向刚度分形模型的必要条件。
1.1 圆锥结合面几何模型
将圆锥结合面沿轴向按等长度分割成N段(N∈∝),并将分割后的每一小段近似看作半径为Riy的圆柱面,如图1所示。

图1 分割后的圆锥结合面几何模型
为了计算圆锥结合面的接触系数λc,在图1中以圆锥连接小端的中心为原点o,以轴向、径向分别作为x轴及y轴建立坐标系xoy,图中R1为圆锥连接小端的半径;B为圆锥有效连接长度;L为B在轴向方向的投影;Riy为第i段圆锥连接界面等效为圆柱连接界面的半径;α为圆锥连接界面的圆锥角。
由图1可得到圆锥结合面有效接触长度B与L的关系式为:
L=Bcosα
(1)
由图1可以确定,圆锥第i段结合面的半径Riy表示为:
Riy=R1+imtanα(i=1,2,…,N)
(2)
式中:m表示每段圆柱片的长度,m=L/N。
1.2 接触系数
根据图1所示的分割后圆锥结合面的几何模型,参考圆柱结合面接触系数[7],可以得到圆锥结合接触系数λc,表达式为:
(3)

当Riy=Riy+1时,两圆锥面完全内接触,λc=0.98。
2 圆锥结合面法向载荷
对于圆锥连接装配体,如图2所示,从加工工艺角度来说,锥体(被包容件)外表面比锥套(包容件)内表面的加工更容易控制,因此在微观尺度上,锥套内表面、锥体外表面分别等效为刚性平面与粗糙表面,该两表面连接形成圆锥结合面。

图2 圆锥连接装配体
圆锥连接装配后,当图2中锥体受到F轴向力时,圆锥结合面将产生法向载荷。粗糙表面各微凸体在法向载荷的作用下发生变形,且各个微凸体之间将产生相互作用,导致粗糙表面微凸体的平均高度发生变化,如图3所示,图中R代表微凸体等效曲率半径,δ为微凸体的变形量,l为微凸体轮廓底面直径,p为法向载荷,r为实际接触面积半径,r′为理想接触面积半径,z为给定微凸体的轮廓高度,d为刚性平面与变形前微凸体平均高度面的距离,dn为刚性平面与结合面在承受法向载荷p变形后微凸体平均高度面的距离,δ′为微凸体间的相互作用而引起的平均高度面的变形量,根据G-W模型[8],假设在锥体与锥套结合面处微凸体接触域为圆形,A为理想接触面积,a为实际接触面积。

图3 微凸体在相互作用下的变形状态图
圆锥结合面接触域上,微凸体相互作用下的单个微凸体的法向载荷为[6]:
(4)
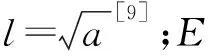
(5)
式中:l为微凸体轮廓底面直径,G为特征尺度参数,D为分形维数。
基于分形接触理论[10],结合文献[11]和1.2节中获得的圆锥结合面接触系数λc带入接触面积为a的面积密度分布函数进行修正,同时引入表示微凸体接触大小分布的域扩展因子ψ,得到圆锥结合面接触面积密度分布函数:
(6)
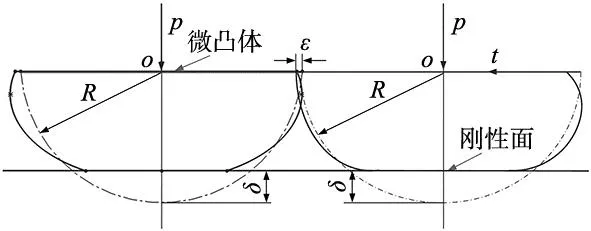
式中:al为圆锥结合面上最大接触点的面积,其中ψ值的大小与分形维数有关,且分形维数与域扩展因子之间满足[12]:
(7)
假设ac为微凸体发生弹性变形与塑性变形的临界接触面积。
当a>ac时,微凸体发生弹性变形,微凸体上的法向载荷为:
(8)
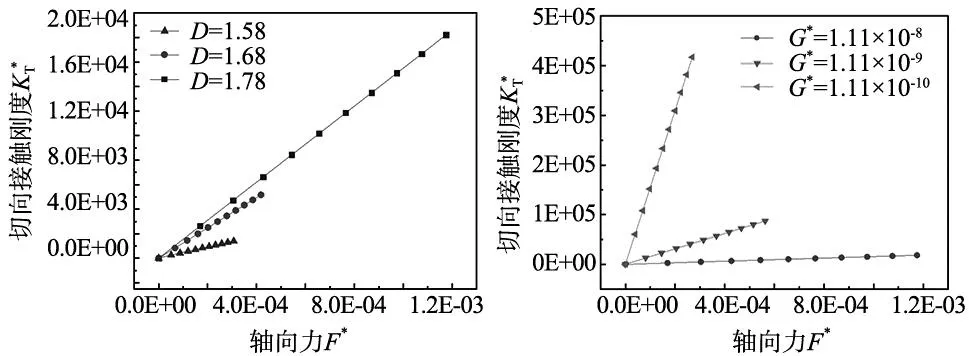
当a pp(a)=kσya (9) 式中:k是与硬度H和屈服强度σy有关的常数,且满足k=H/σy。 在锥体持续承受轴向力时,圆锥结合面上接触域微凸体将发生弹性变形和塑性变形,则微凸体上法向载荷可认为弹性载荷与塑性载荷之和。在这个状态下,对微凸体接触面积函数n(a)积分可得到圆锥结合面接触全域上的法向载荷: (10) 对式(10)进行积分整理后,推导得到综合考虑微凸体相互作用和引入域扩展因子ψ后的圆锥结合面法向载荷为: (11) 整理得圆锥结合面无量纲法向载荷P表达式为: (12) 考虑到微凸体相互作用的因素后,当单个微凸体受法向载荷p和切向载荷t后,两个微凸体之间产生切向变形量为ε,如图4所示。并存在如式(13)关系[13]: 图4 微凸体相互作用影响下的切向变形图 (13) 根据式(13),结合文献[6],推导得到微凸体相互作用下的单个微凸体的切向刚度模型: (14) 随着局部法向接触载荷的逐渐增大,发生塑性变形的微凸体将产生塑性流动,切向刚度趋近于零。因此在建立圆锥结合面的切向刚度模型时,只需考虑发生弹性变形的微凸体,则结合面的切向刚度KT可以表示为: (15) 在同时考虑域扩展因子ψ、圆锥结合面接触系数λc、最大接触点的面积al和实际接触面积Ar时满足关系: (16) 将式(6)、式(14)带入式(15)得到圆锥结合面接触全域上的切向刚度KT: (17) 根据文献[14]得知作用于单个微凸体的法向载荷p与切向载荷t之比满足T/P=t/p,其中T为结合面切向载荷,且T=τbAr(τb为锥体材料的剪切强度)。对圆锥结合面切向刚度KT进行无量纲化处理,对式中切向刚度KT、法向载荷P、临界接触面积ac进行无量纲化,即各个参数所对应的形式为: (18) 高速主轴作为高性能加工中心关键部件,其内部结构中的主要组件主轴-刀柄连接是圆锥连接的典型应用,如图5所示。本文依据3.2节建立的圆锥结合面切向刚度模型,从微观尺度对拉刀力(轴向力)加载过程中的主轴-刀柄连接装配体圆锥结合面切向刚度进行分析探讨。 图5 主轴-刀柄圆锥连接示意图 在主轴-刀柄圆锥装配体中,作为被包容件的刀柄受力分析如图6所示,图中R0为刀柄大端半径,R1为刀柄小端半径,α为圆锥角度,在主轴-刀柄宏观结合面处,P为结合面均布法向载荷,且处处相等,KT为结合面切向载荷,F为刀柄所受拉杆轴向力,L为刀柄的轴向长度。 图6 刀柄受力示意图 某高速主轴-刀柄的实测几何参数如表1所示,材料参数如表2所示。 表1 刀柄实测的几何参数 表2 主轴-刀柄材料的参数 由图6可得,R0、R1与刀柄锥面的面积Aa之间满足关系[15]: (19) 式中:R1与R0满足R1=R0-Ltanα。 刀柄锥面法向力P与刀柄拉刀力(轴向力)F满足: P=Fsinα (20) 假设主轴-刀柄圆锥结合面在宏观上所受载荷P是均布的,则在微观尺度上是一个均匀的接触状态,建立法向载荷模型和切向刚度模型时,首先需要确定微凸体临界接触面积ac和接触面上最大接触点的接触面积al,但接触面积al在微观尺度上很难直接得到,可借助式(20)刀柄受F轴向力间接计算得到圆锥面法向载荷P,结合式(11)可以得到微凸体接触面积al,将所得接触面积al带入式(16)可得出实际接触面积Ar。 刀柄表面轮廓和粗糙度通过针式表面粗糙度仪测量,采样长度为0.8 mm,采样步长为0.5 μm,粗糙度Ra为0.6。得刀柄的表面轮廓,如图7所示。 图7 刀柄表面轮廓曲线 选用结构函数法[16]计算得到刀柄表面的分形参数,在粗糙度Ra=0.6时刀柄对应的分形维数和特征尺度参数如表3所示。 表3 刀柄表面的分形参数 并将上述得到的主轴-刀柄结合面的分形参数带入所建圆锥结合面分形模型中,得到主轴-刀柄结合面切向刚度值,如图8所示。通过与文献[17]主轴-刀柄实验结果进行对比,可以得知本文建立的圆锥结合面切向刚度模型有较好的准确性,更符合实际的接触情况。 图8 理论与实验结果比较图 为了便于数据的分析比较,分形参数的取值将在实际计算值的附近取值,则分形维数D的取值分别为1.58、1.68、1.78;无量纲的结合面分形特征尺度参数G*取值分别为1.11×10-8、1.11×10-9、1.11×10-10。经计算h=T/P其取值分别为0.078、0.109、0.136;刀柄材料的特性系数φ的取值分别为0.003、0.004、0.005。 (a) 不同分形维数D下与F*关系 (b) 不同特征尺度参数G*下与F*关系 根据上述曲线图对其进行详细分析,讨论刀柄轴向力的变化在不同参数下对主轴-刀柄结合面切向刚度的影响趋势: (1)由图9a分析可知:在特征参数G、特性系数φ、不同比值h等参数不变的前提下,随着轴向力F的逐渐增大,切向刚度也逐渐增大。这是因为当结合面法向接触载荷逐渐增大时,主轴-刀柄圆锥结合面上的微凸体发生弹性变形的数量占结合面总微凸体的比例会更大;轴向力F相同的情况下,分形维数D越大则切向刚度越大,这是由于结合面的分形维数D能够反映出物体表面的粗糙程度,当结合面分形维数D增大时,表面粗糙度越小。结合面发生弹性接触的微凸体数目增多,从而结合面切向刚度增大。 (2)由图9b分析可知:在分形维数D、特性系数φ、不同比值h等参数不变的前提下,在相同轴向力F时,特征尺度参数G越小,表面越光滑,切向刚度就越大。所以减少结合面特征尺度参数G有利于提高结合面切向刚度;主轴-刀柄圆锥结合面切向刚度随着轴向力F的增大与特征尺度参数G的减小近似成线性关系,且特征尺度参数G越小结合面切向刚度增长趋势越明显。 (3)由图9c分析可得:在分形维数D、特征参数G、不同比值h等参数不变的前提下,主轴-刀柄切向刚度随着φ的增大而逐渐增大。因为随着φ的增大,可知材料的屈服强度σy也增大。临界接触面积ac将减小,接触面间的弹性接触的比例增大,导致结合面的切向刚度增大;考虑微凸体相互作用和域扩展因子时,在分形参数不变的情况下,φ越大切向刚度增大的趋势越明显。 (4)由图9d分析可知:分形维数D、特征参数G、特性系数φ等参数不变的前提下,从图中曲线可以看出,在相同的法向载荷下比值h越小则主轴-刀柄圆锥结合面处切向刚度越大;在主轴-刀柄圆锥结合面处,当切向载荷T一定时,随着比值h=T/P的逐渐减少,此时法向载荷P随之增大,即意味着轴向力F也随之增大。推得适当提高拉刀力F则有助于提高主轴-刀柄圆锥结合面处切向刚度。 本文在考虑微凸体相互作用的条件下,引入域扩展因子建立较为准确的圆锥结合面且切向刚度接触分形模型,得到了轴向力加载过程中的分形参数、材料特性系数等对其切向刚度的影响规律,分析得如下结论: (1)选择特性系数φ较大的锥体(刀柄)材料,或者增大分形维数D,即降低主轴-刀柄结合面粗糙度,可适当提高结合面切向刚度KT。 (2)轴向力F的增大有利于提高主轴-刀柄结合面的切向刚度KT,因此,适当选取合适的拉刀力可以提高结合面切向刚度KT,对主轴-刀柄拉刀力的设计提供理论参考。
3 圆锥结合面切向刚度
3.1 微凸体相互作用下的单个微凸体切向刚度

3.2 圆锥结合面全域上的切向刚度

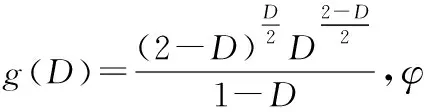
4 算例应用

4.1 切向刚度模型的实验验证





4.2 轴向力加载过程中的各参数对主轴-刀柄切向刚度的影响

5 结论

