基于混合机器学习模型的建筑工程造价预测方法*

李姣姣

(合肥城市学院 安徽合肥 230601)

随着科技和经济的不断发展，建筑工程也逐渐复杂化、大型化[1]。目前关于建筑工程造价预测的方式多集中在住宅建筑方面，同时大多通过单一的机器学习算法进行预测，这就导致适用性不强，精确度偏低的问题[2-4]。文章旨在通过多种算法结合支持向量机进行对比，从中选择最优的混合模型。

1模型指标确定与预处理

1.1输入量及预处理数据

通过企业信息收集以及造价信息网等方式，对某市新建建筑工程信息进行收集，共收集52例项目。经过分析以及筛选，得到39例样本工程数据，由此组成的箱型图如图1所示。

图1 单方造价箱型图

由图1得到的数据包含两种类型：描述型和数字型。针对描述型，工程造价在进行特征量化时按照从低到高的顺序进行。如装修标准中，毛坯房为1，简装为2，精装为3，暖通方面由低到高分为1～4级，其中1级粗糙度最高；针对数字型，按照对应的数值分析量化数据。量化后借助SPSS进行对应的标准化，所得数据如表1所示。

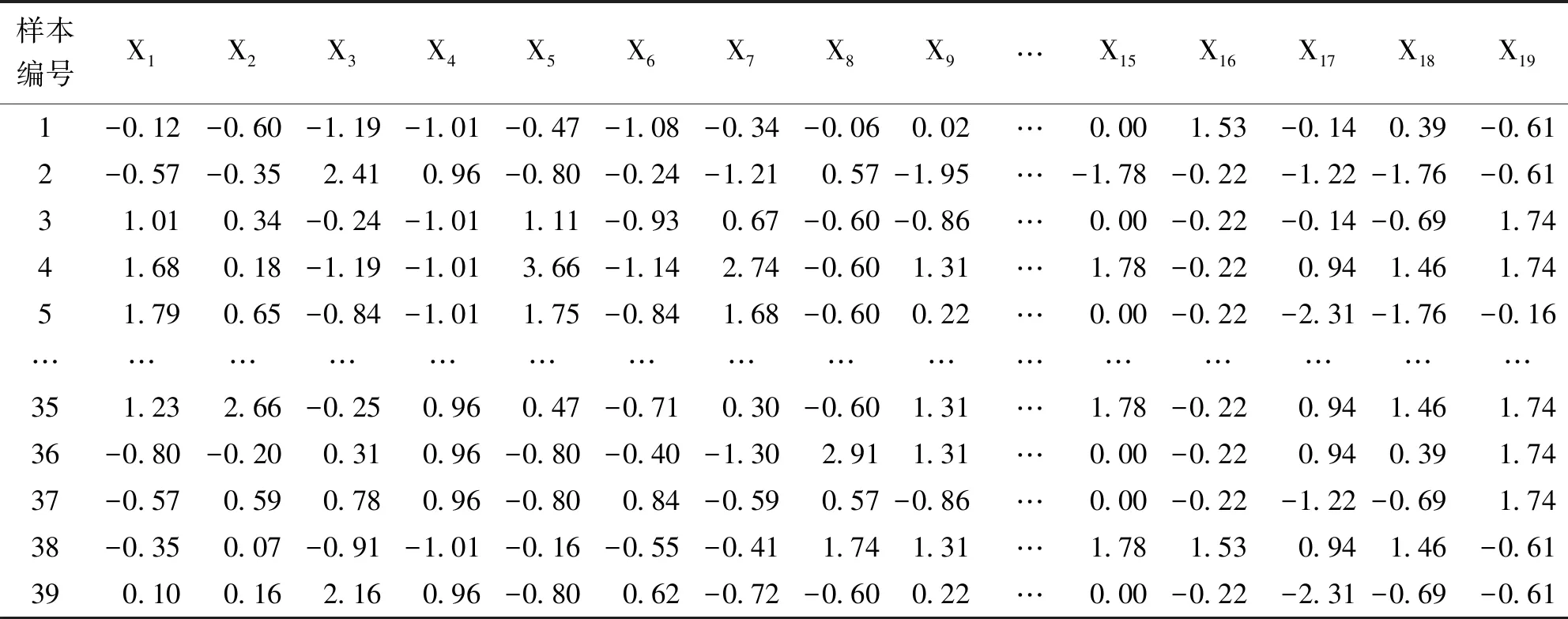
表1 标准化工程造价数据节选

表1中，节选了部分标准化的数据。其中，样本数据类型说明如表2。

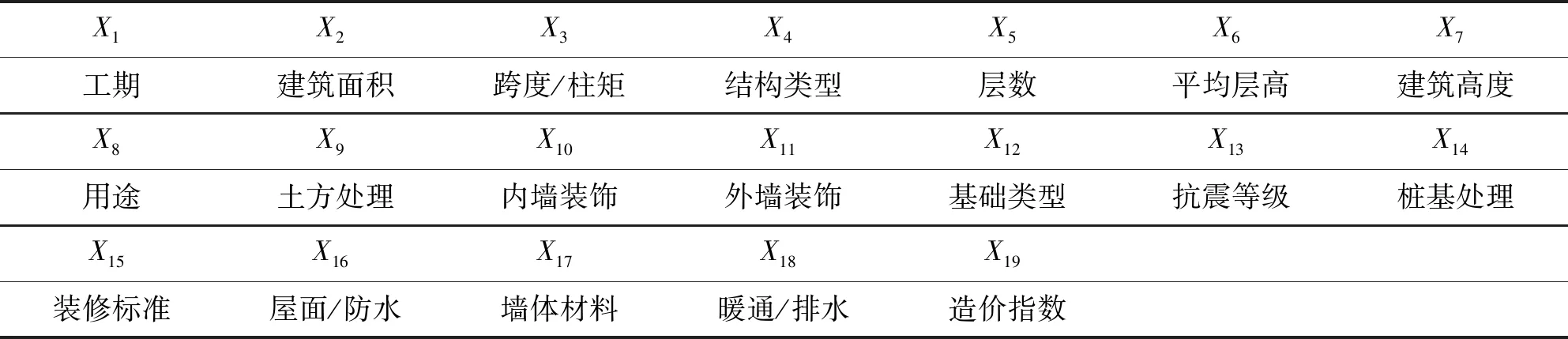
表2 样本数据类型说明

结合表2，各数据类型正则化后均在3标准差内，符合实际的数据需求。

1.2降维主成分分析

通过对多变量向少量主成分进行转化，由综合的数据指标对原始数据的特征信息反应即主成分分析。主成分分析的方法一是可以避免不同影响因素相互的关联性影响实际预测，而是可以避免输入量过多产生的过拟合问题。对筛选所得的39例样本工程数据进行主成分分析，通过降维进行少量主成分的等效转化。

以标准化为基础，对给定指标值构建相应的矩阵，如下所示：

(1)

式(1)的39×19阶矩阵中，结合SPSS中矩阵的相关性理论，对变量的相关性进行Bartlett＇s球形检验以及相应的KMO检验，所得结果如表3所示。

表3 相关性检验结果

表3中，Bartlett＇s检验所得应小于0.001，KMO检验所得值应大于0.7。Bartlett's检验值为0.000，KMO检验所得值0.717，均符合要求，也即数据输入结构合理，能够记性进一步的主成分分析。

对主成分特征值以及贡献率等进行分析，所得结果如表4所示。

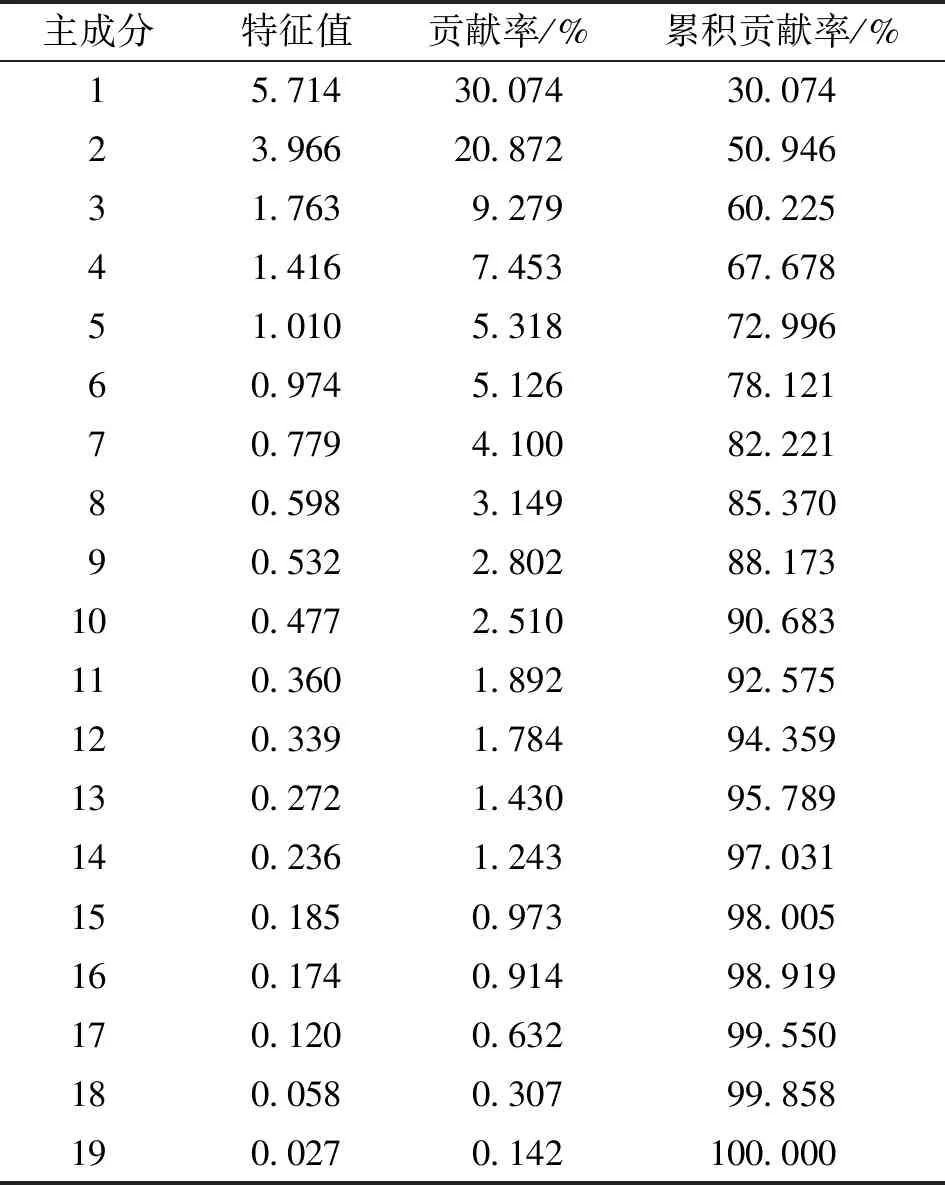
表4 主成分特征值与贡献率分析

在主成分分析中，通常要求总方差即累计贡献率超过80%，符合主成分结束的要求。方案设计将该值设定为85%，结合表4，对前8个贡献率较高的进行提取，其累计贡献率为85.530，满足总体解释需求。同时，数据因子的提取需结合造价数据碎石，如图2所示。

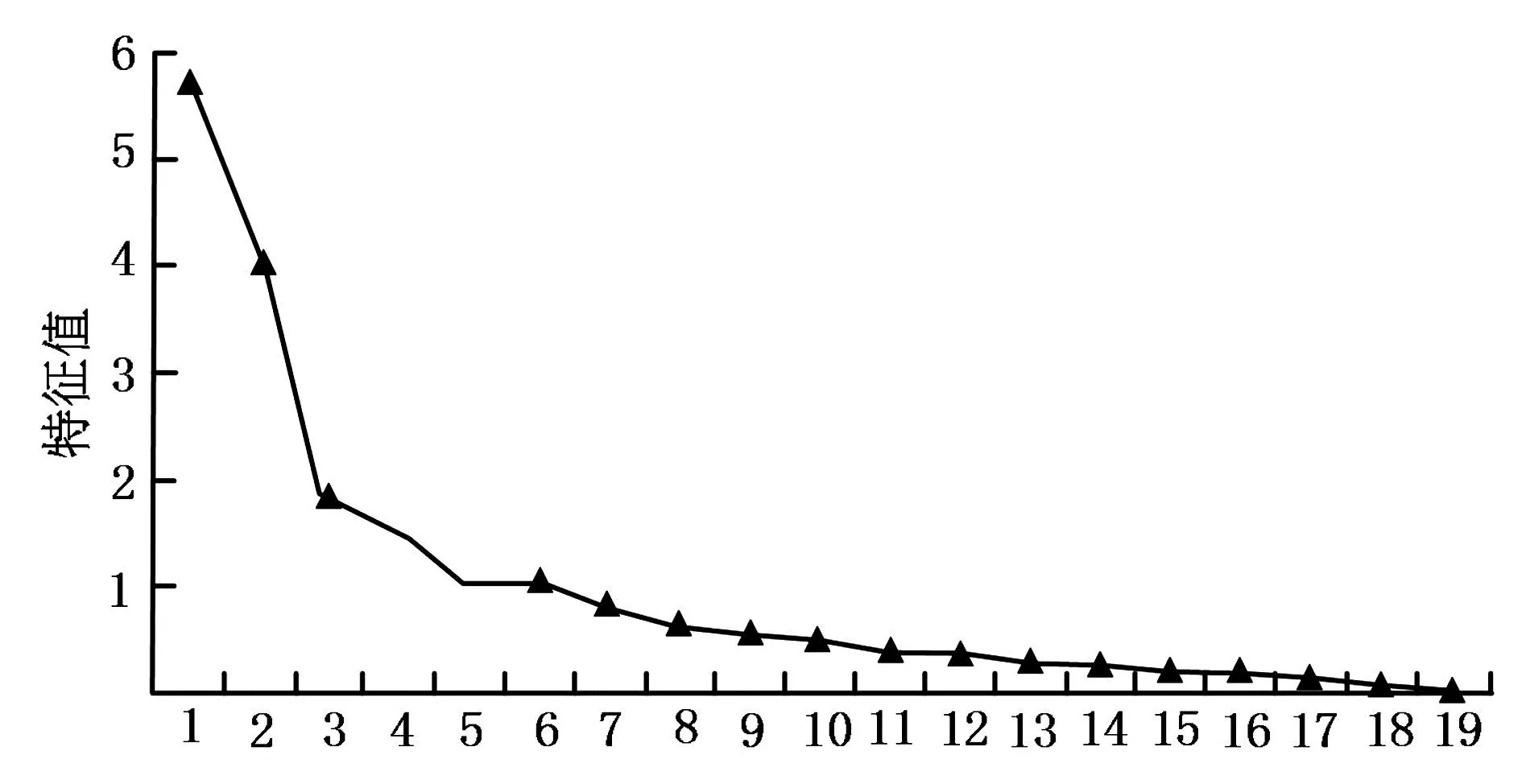
图2 造价数据碎石图

图2中，在第8个数据因子中出现较为明显的拐点，对前8个数据提取满足实际分析需求。

1.3分析灰色关联

在非线性以及多因素的分析问题中，灰色关联的方式应用广泛。灰色关联主要通过对序列曲线对应的集合相似度来进行不同序列关联度的判断，序列关联度越大，序列曲线的形状越相似。灰色关联是一种有序的相关性分析方式，其计算公式如公式(2)。

ξ0，1(k)=

(2)

式(2)中，分辨系数用ρ表示，对应的参考序列用x0(k)表示，指标个数用m表示，对象个数用n表示。其中i=1，2，…，n，k=1，2，…，m。

对应的关联序通过公式(3)进行计算。

(3)

通过DPS分析39个项目案例与数据因子的灰色关联，分析时分辨系数的值设定为0.5，得到的关联度如表5所示。

表5 因子与工程造价之间的关联度

表5中，结合工程造价中实际的重要影响因素以及关联度排序数据，从中选择X18、X17、X15、X12、X4、X6、X5、X2、X19共9项数据因子作为预测模型的输入集。

2算法处理

对预测模型性能的进一步提高，通过结合BP神经网络、SVM支持向量机以及BP神经网络完成。

2.1 BP神经网络

BP神经网络包括输出层、隐含层以及输入层，实际运行时，误差进行反向反馈。模型设置的BP神经网络为3层，对连续函数进行拟合，其经验公式如公式(4)。

p=1bd

(4)

其中，p应满足公式(5)的约束条件。

(5)

式(4)、式(5)中，隐含层对应的节点数用p表示，输入层对应的节点数用d表示，输出层对应的节点数用f表示。a为常数，a∈[1，10]。

2.2 SVM支持向量机

SVM支持向量机的应用主要针对非线性的分类与回归。其原理主要是在高维特征空间当中进行数据因子的非线性映射，将待求解问题进行向二次优化的问题转化，提高对应的鲁棒性。

2.3算法优化

算法优化主要结合粒子群算法、遗传算法以及交叉验证法，从而进行参数的最小化寻优，以提高模型的精确度。粒子群算法能够通过更少的参数实现结果寻优，但更新迭代仅通过内部速度完成。遗传算法可以结合环境进行个体适应度的选择，需要确定种群规模、遗传迭代次数以及对应的变异概率。模型在对于交叉验证方式的选择上，采用K-CV的方式，该种方式计算效率更高，更加适合SVM支持向量机的参数优化。

3结果分析

3.1主成分预测模型分析

3.1.1 BP神经网络模型预测 BP神经网络模型中，选择正切S性tansig函数未对应的传递函数，选取trainlm为对应的训练函数。设定训练速度的值0.1，训练目标的值0.01，训练补偿的值为100，通过公式(4)进行隐含层的确定，不同隐含层对应的决定系数如表6所示。

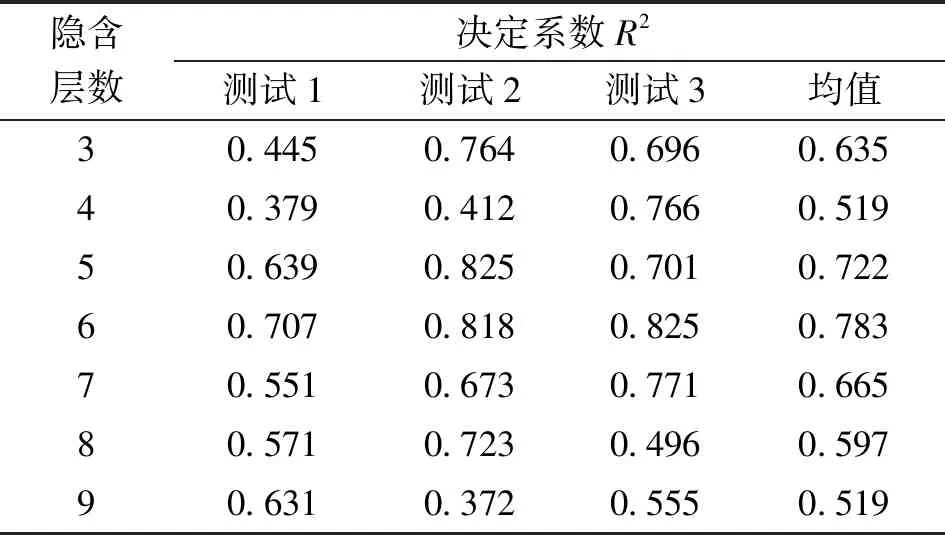
表6 隐含层数决定系数

表6中，当隐含层数为6时，决定系数的均值最大，选择隐含层数为6。模型预测通过GA-BP模型以及PSO-BP模型进行预测。对39组样本数据进行随机抽取，其中测试样本数量为7，训练样本数量为32。输入变量为提取到的8个数据因子，输出为对应的建筑工程造价，各模型运行11次，以准确率第6的结果为最终结果。

通过GA-BP模型预测的适应度曲线以及预测结果如图(3)及图(4)所示。

图3与图4的GA-BP模型中，输入层的神经元个数为8，输出层的神经元个数为1，隐含层的神经元个数为6。初始值设定上，迭代为50次，变异率为0.1，对应的种群数为20。通过PSO-BP模型预测所得的适应度曲线以及预测结果如图(5)及图(6)所示。

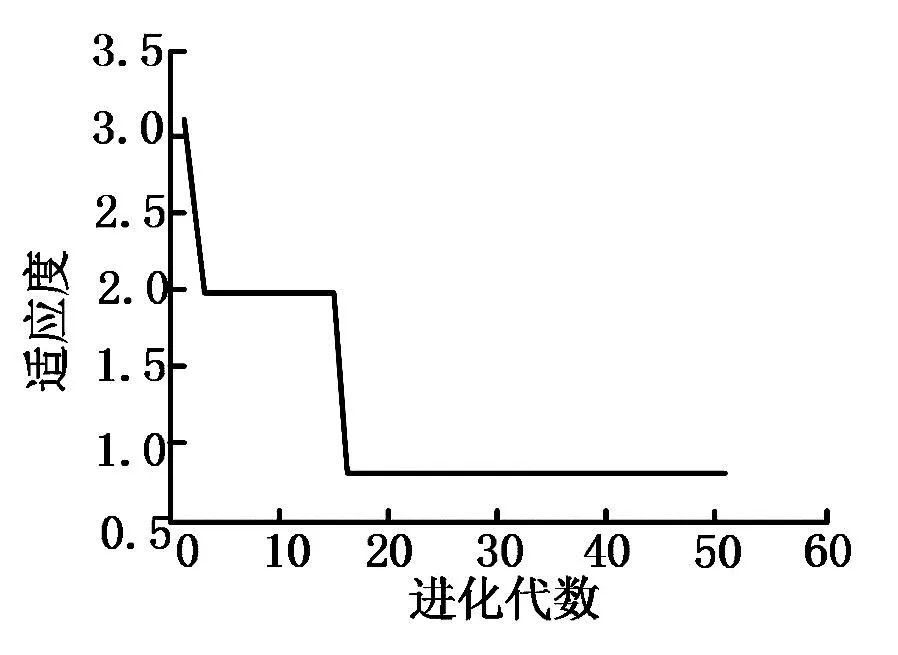
图3 GA-BP适应度曲线

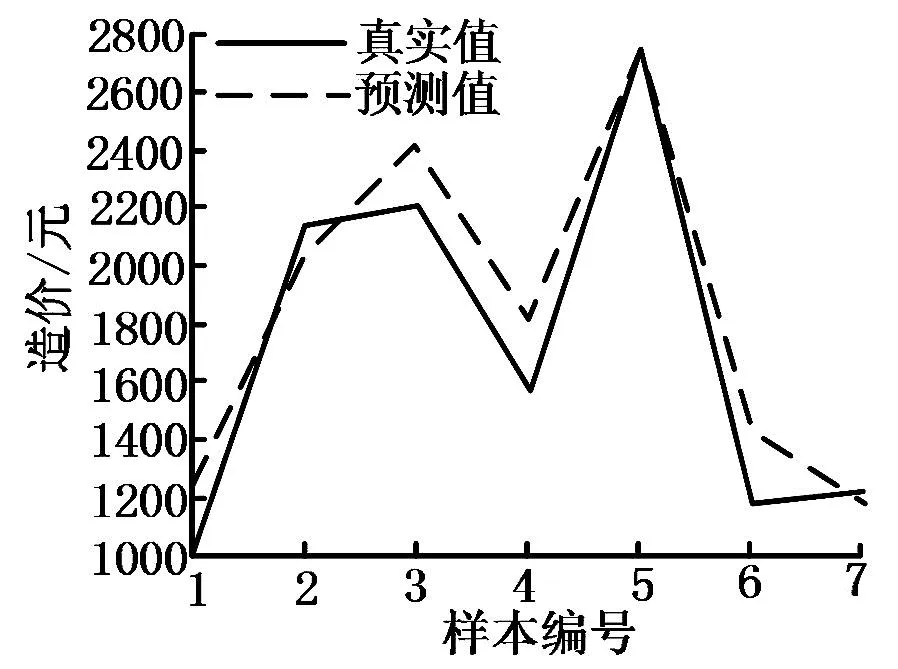
图4 GA-BP模型预测结果

图5 PSO-BP适应度曲线

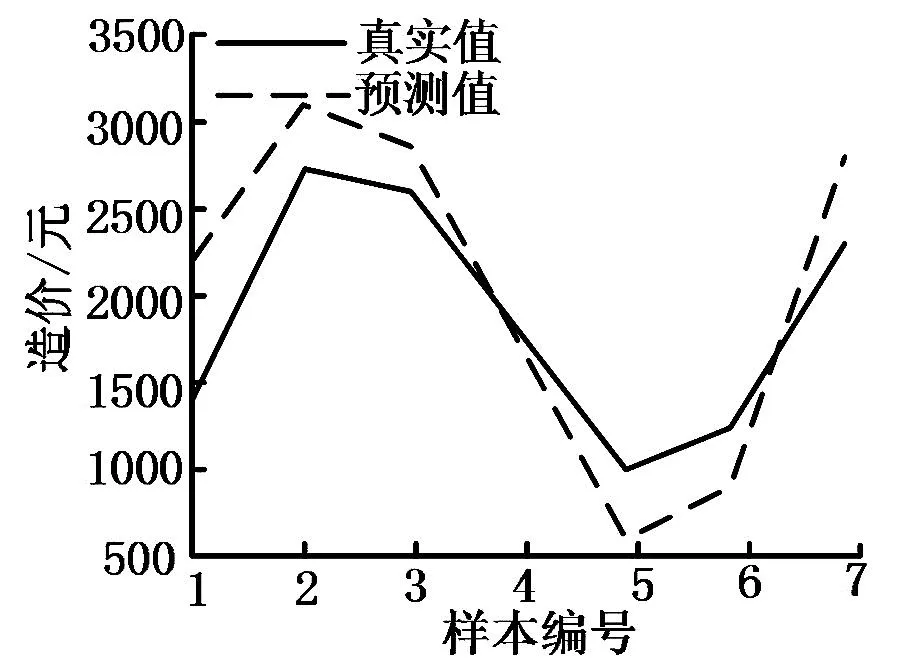
图6 PSO-BP模型预测结果

神经网络的网络结构设定为8-6-1，初始化设定上，迭代为80次，学习因子均设置为2，PSO规模设定为30。

3.1.2支持向量机模型预测 通过交叉算法对支持向量机进行优化，所得的最终预测结果图形如图7所示。图7中，惩罚参数c设定为eh，核函数的参数g设定为eb。回归参数粗选时设定步长1，h=[-8，8]、b=[-8，8]，最终惩罚参数的值为16，核函数参数的值为0.1184。由粗选结果进行精选时，设定步长为0.5，h=[-5，5]、b=[-5，5]，求得的惩罚因子为4，核函数的参数为0.0625。

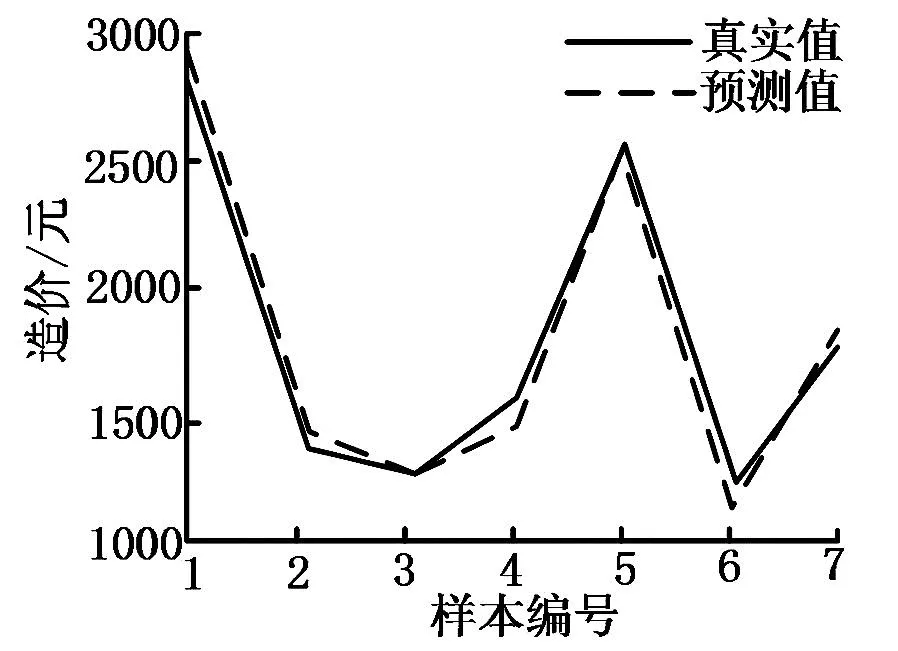
图7 交叉算法优化向量机预测结果

通过GA-BP对向量机进行优化，得到的测试预测结果如图8所示。

图8 GA-BP优化向量机预测结果

图8中，设定种群规模120，进化代数最大为200，最终得到的惩罚因子为23.6388，核函数参数的值为20.8472。通过PSO-BP对向量机进行优化，得到的测试结果如图9。图9中，设定种群规模120，进化代数最大为200，最终得到的惩罚因子为2.9405，核函数的参数为1.9617。

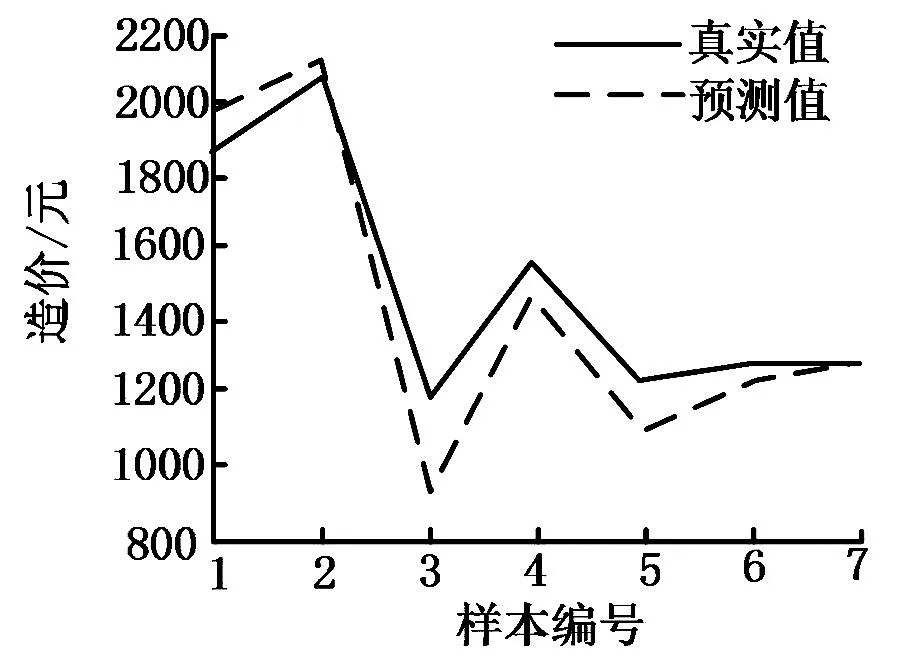
图9 PSO-BP优化向量机预测结果

3.2灰色关联模型

通过GA-BP对灰色关联模型优化后的预测结果如图10所示。

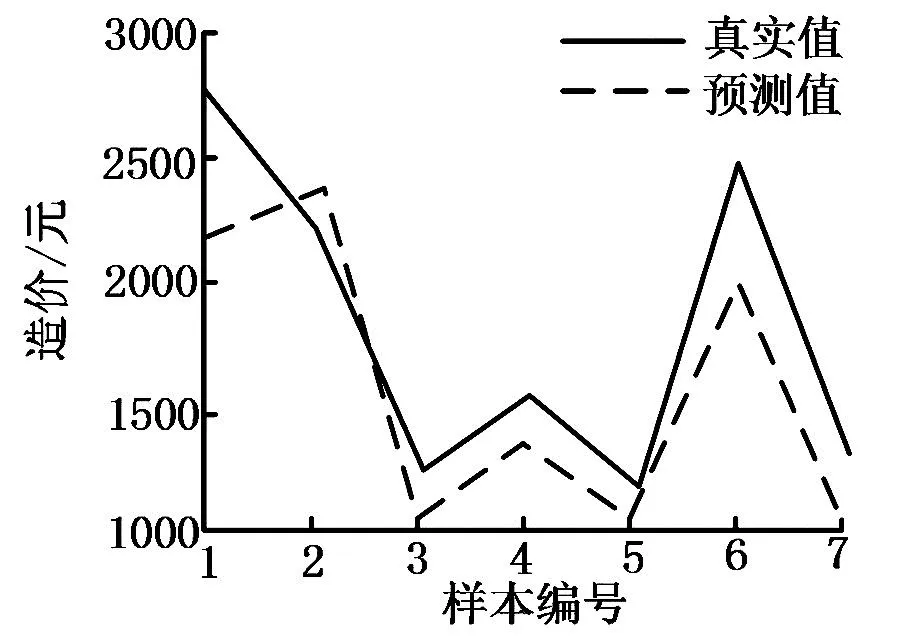
图10 GA-BP优化灰色关联预测结果

图10中，种群数初始值设定为20，迭代设定为80次，变异率设定为0.1。通过PSO-BP对灰色关联模型优化后的预测结果如图11。图11中种群规模设定为30，迭代设定为80次。通过交叉算法对灰色关联模型进行优化，并结合SVW支持向量机，得到的预测结果如图12所示。

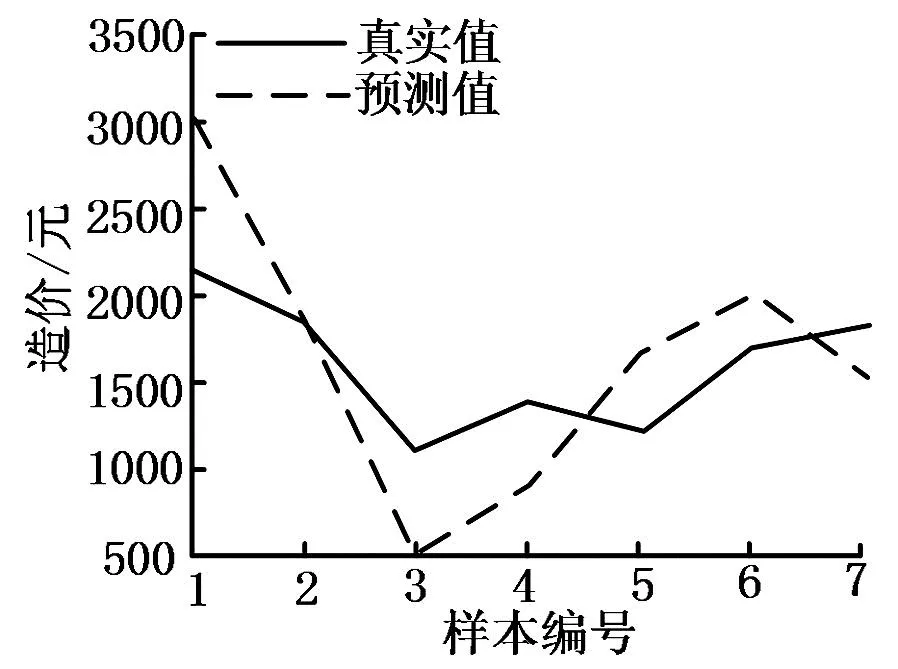
图11 PSO-BP优化灰色关联预测结果

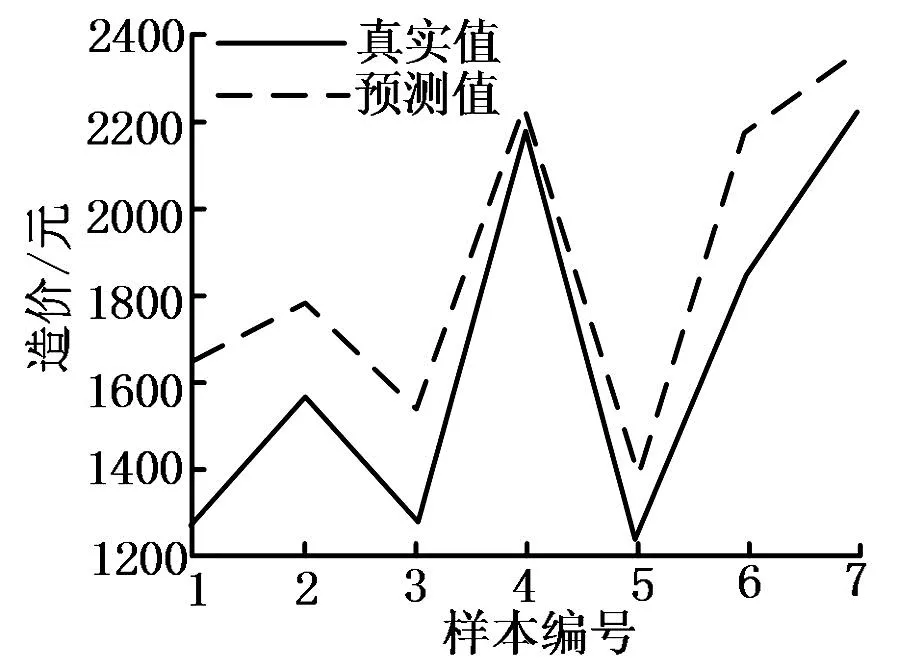
图12 交叉算法优化灰色关联-SVW预测结果

图12中，交叉算法参数设置与前文相同，求得惩罚因子的值为2，核函数参数的值为0.0442。

通过GA-BP优化灰色关联并结合SVW向量机的预测结果如图13所示。图13中，最终求得的惩罚因子数值为84.1303，核函数参数的值为35.3061。通过PSO-BP优化灰色关联并结合SVW向量机的预测结果如图14所示。

图13 GA-BP优化灰色关联-SVW预测结果

图14 PSO-BP优化灰色关联-SVW预测结果

图14中，最终求得的惩罚因子的值为0.9966，核函数参数的值为5.7113。

3.3预测模型结果对比

对应预测模型所得结果进行汇总，详见表7。

表7 预测模型结果汇总

表7中，R2为对应的决定系数，其值越高则代表由越高的精确度。通过整体对比，主成分分析(PCA)的方式进行预测的精确度要优于灰色关联分析(GRA)的精确度。同时，通过算法对支持向量机进行优化相对误差均在10%，优于单纯算法预测模型的结果。综上，通过交叉算法(CV)优化向量机进行主成分分析的结果最优。通过该办法预测后的效果对比如表8所示。

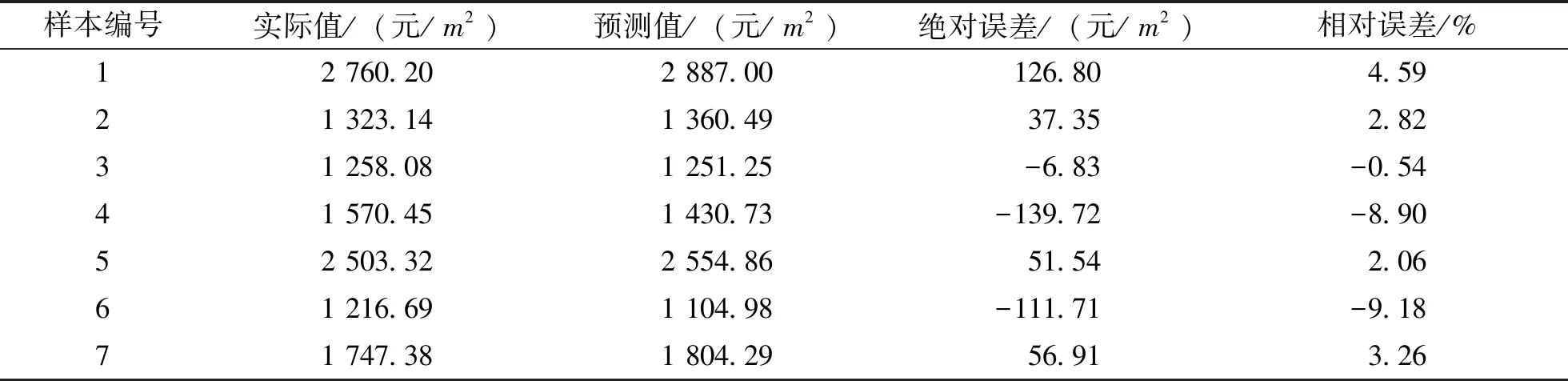
表8 交叉算法优化向量机主成分分析结果

表8中，预测的相对误差均在10%之内，整体预测结果接近实际数值，符合实际环境中工程造价预测需求。

4结语

传统的工程造价预测模型同场存在误差较大、适用性有效以及计算繁琐等问题。通过交叉算法对支持向量机进行优化，结合主成分分析的方式，进行建筑工程造价预测，能够最大化简化计算步骤，提高造价预测的精确度。同时，该办法广泛适用于各类建筑工程造价预测。经过实验验证，方法切实可行，能够应用于实际生产工作中。