改进粒子群算法优化支持向量机的螺旋CT电气故障诊断研究*
汤德荣
(安徽机电职业技术学院 安徽芜湖 241002)
CT技术的医学价值在医学领域发挥的作用一直不容小觑[1]。传统CT设备在进行医学扫描时经常出现间断扫描情况,加之扫描的速度比较慢,常常无法将所需的医学信息完整地提取出来。近年来,在医学领域主要应用螺旋CT取代普通CT在临床方面协助医生对患者的病情进行有效诊断。
螺旋CT可实现螺旋式的连续不间断永久扫描,与普通的CT相比,扫描的效率与信息提取的精度以及提取信息的完整程度均较高。但是在使用螺旋CT进行病人病情诊断时,由于操作者对设备使用不当、硬件部分损坏以及一些环境因素常会导致在使用螺旋CT协助医生进行病情诊断时出现CT电气故障现象,故障现象的出现,给病情的诊断带来了巨大阻碍,遇到一些紧急状况,由于延误病情诊断时间,甚至可能会危害患者的生命安全。为了有效降低或避免此种状况的发生,国内外诸多学者针对螺旋CT可能发生故障的诊断方法进行了大量研究。在诸多故障诊断方法中,比较受欢迎的有谢锋云等人研究的基于多特征提取和LSSVM的故障诊断方法[2]、石志标等人研究的基于CEEMDAN与CBBO-SVM的故障诊断方法[3]。这些方法能够较好实现对螺旋CT电气故障的诊断,但是其泛化以及故障诊断时的迭代能力较差,使得螺旋CT电气故障诊断具有一定的局限性,并且诊断效率较低[4]。
最小二乘支持向量机(LSSVM)作为一种基于大样本数据分类算法,可实现大样本数据有效分类。改进粒子群算法(PSO)在进行问题求解时,具有较强的迭代与优化参数能力。将改进粒子群算法与最小二乘支持向量机结合起来用于螺旋CT电气故障的诊断过程中,可大大提高故障诊断的泛化能力与诊断效率[5]。为此,文章研究改进粒子群算法优化支持向量机的螺旋CT电气故障诊断方法,螺旋CT电气故障诊断效率与诊断精度更高,可更好满足实际螺旋CT电气故障诊断工作需要。
1结合改进PSO和LSSVM的螺旋CT电气故障诊断
1.1基于LSSVM的螺旋CT电气故障诊断
在进行螺旋CT电气故障诊断时,将最小二乘支持向量机算法(lest squares support vector machines,LSSVM)应用于螺旋CT的故障诊断中,因其具有很强大的分类能力与学习能力,可有效区分螺旋CT的故障类型,完成对螺旋CT电气故障的有效诊断[5]。最小二乘支持向量机的工作原理具体可表述如下:
(1)将螺旋CT电气故障样本数据的非线性映射用公式定义为Z=Φ(。)。
(2)选取n维输入螺旋CT电气故障样本向量,1维输出螺旋CT电气故障诊断结果向量。
(3)执行样本向量从原空间到高维特征空间的映射操作。
(4)在高维特征空间中构建最优函数。
(5)通过最优函数拟合螺旋CT电气故障样本数据。
用公式可将最优函数表示为:
f(x)=ωTφ(x)+b
(1)
对高维特征空间存在的点积运算执行替换操作,将其替换成原空间的核函数,设结构风险与正规化因子表示为R(ω)与C,容许误差与非线性变换函数表示为ξ与φ,则关于式(1)有:
(2)
将螺旋CT电气故障诊断最优解的求解转换为高维空间最优分类面的求解可通过非线性变换函数φ实现。为使最优分类面的求解即螺旋CT电气故障诊断结果更准确与便捷,将拉格朗日函数用于最优分类面的求解过程中,具体的求解过程用公式可表述为:
(3)
式(3)中,拉格朗日乘子用αi代表。
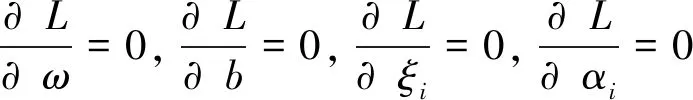
则有:
(4)
其中,i=1,2,…,N。
对式(4)执行ω与ξ消除操作,则有:
(5)
式(5)中,I∈R(N×N),并且Z、Y、1v、ξ与α分别满足:
(6)
Y=[y1,…,yN]
(7)
1v=[1,…,1]T
(8)
ξ=[ξ1,…,ξN]T
(9)
α=[α1,…,αN]T
(10)
设定Q=ZZT=(qij)N×N,核函数表示为:
K(xi,xj)=φ(xi)。φ(xj)
(11)
根据Mercer原则,有:
qij=yiyjK(xi,xj)
(12)
径向基函数RBF在解决问题时的运算复杂度较低,并且整个运算过程只存在唯一的参数σ。因而文章将其作为核函数对相关问题进行求解。其用公式表示为[6]:
K(xi,xj)=exp(-‖xi-xj‖/σ2)
(13)
通过对以上问题进行求解可将最优分类函数用公式表示为:
(14)
通过式(14)便可获取螺旋CT电气故障诊断结果
1.2改进PSO的LSSVM模型参数优化
利用LSSVM模型进行螺旋CT电气故障诊断的过程中,模型核函数是否呈现最优状态,关系到整个螺旋CT电气故障诊断的优劣,因而根据交叉验证的相关论述,应用改进粒子群(PSO)算法优化最小二乘向量机(LSSVM)的参数-核函数,更好完成螺旋CT电气故障的有效诊断。
定义一个粒子数量为S的种群X,用公式将其表示为X={X1,…,Xs,…,XS},将其在d维的搜索空间内的飞行速度用公式表示为νs=[νs1,νs2,…,νsd]H,满足s=(1,2,…,S)。如果将第s个粒子执行最优位置搜索操作得到的最优位置用公式表示为Ps=[Ps1,Ps2,…,Psd]H,其中Psd代表在d维的搜索空间内由s粒子进行最优搜索得到的最优解,则根据粒子历史行为动态调整与靠近最优搜索位置的特性,可将粒子群(PSO)算法用公式表示为:
νsd(h+1)=νsd(h)+c1(h)r1(h)(Psd(h)-xsd(h))+c2(h)r2(h)(Pgd(h)-xsd(h))
(15)
xsd(h+1)=xsd(h)+νsd(h+1)
(16)
上述公式中,进化代数用h代表;r1(h)与r2(h)代表随机变量,在h(0,1)间的分布呈均匀状态;加速常数用c1(h)与c2(h)代表;h代内第s个粒子的位置与群内各个粒子执行搜索操作得到的最优位置分别用xsd(h)与Pgd(h)代表。
在应用粒子群算法求解一些实际问题时,尽管其具有较好的收敛性能,但是常常在寻求最优解的过程中,呈现局部最优状态,无法使算法达到全局最优,为此将惯性权重引入到粒子群算法中,达到控制与改善粒子群算法寻优性能的目的。引入惯性权重以后,可将粒子权算法用公式表示为:
νsd(h+1)=ω(h)νsd(h)+c1(h)r1(h)(Psd(h)-xsd(h))+c2(h)r2(h)(Pgd(h)-xsd(h))
(17)
xsd(h+1)=xsd(h)+νsd(h+1)
(18)
ω(h)代表惯性权重,将初始惯性权重表示为ω1,终止惯性权重表示为ω1。则ω(h)的迭代过程用公式可表示为:
(19)
式(19)中,最大进化代数为H。
当进化代数的值等于t时,用公式可将加速常数c1(h)与c2(h)表示为:
(20)
式(20)中,c1(h)执行从c1i到c1f的连续减少操作;c2(h)执行从c2i到c2f的连续增加操作。
通过上述改进完成的PSO算法对LSSVM模型的核函数进行最佳寻优,提升LSSVM模型螺旋CT电气故障诊断效果
1.3螺旋CT电气故障诊断流程
粒子Xs表示为一个集合{ C,σ},想要验证经改进粒子群算法优化最小二乘向量机参数后,支持向量机的性能是否达到理想性能,可以通过与改进粒子群算法适应度函数相关的平均分类准确率反映出来。为此,用lTq代表第q个验证集中正确分类螺旋CT电气故障数据数量,则可将适应度为p折CV时的平均分类准确率用公式表示为:
(21)
式(21)中,lq表示验证集的螺旋CT电气故障样本数量。螺旋CT电气故障诊断流程如图1所示。
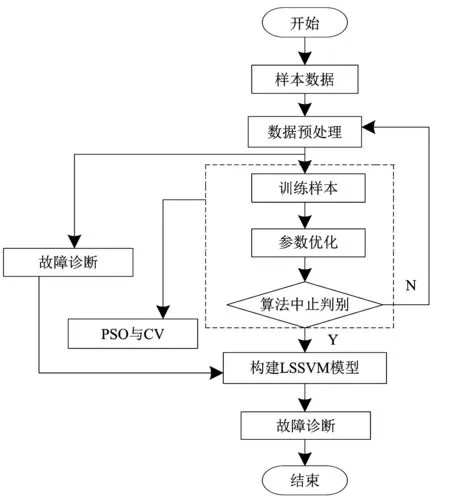
图1 螺旋CT电气故障诊断流程图
螺旋CT电气故障诊断的主要步骤可归结如下:
(1)采集有效的螺旋CT电气故障诊断数据。
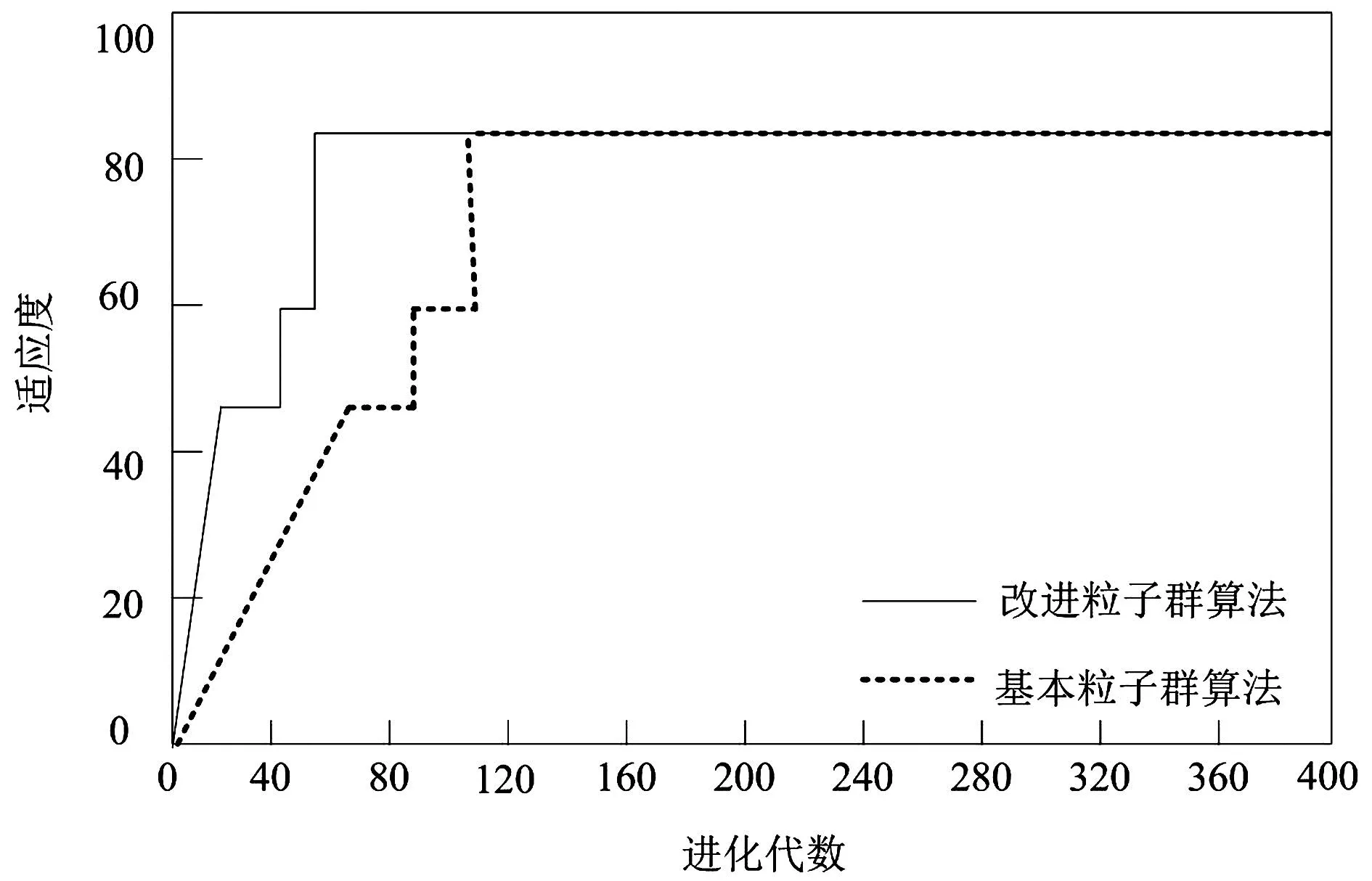
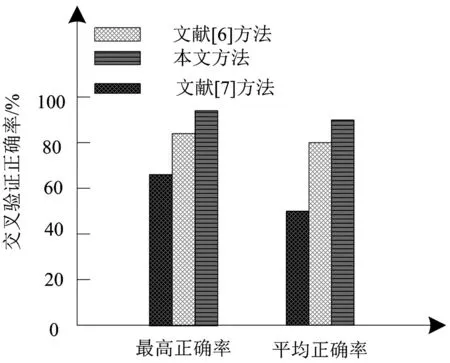
(2)对采集到的螺旋CT电气故障数据执行尺度变换操作。如果用公式将变换的范围表示成[a,b],满足a (22) 式(22)中,螺旋CT原始故障数据样本里的最大与最小样本值分别用xmax与xmin代表。 (3)在尺度变换后的螺旋CT电气故障数据样本中选取两部分数据,分别作为螺旋CT电气故障诊断的训练样本与测试样本。 (4)根据CV理论的阐述,将改进粒子群算法与最小二乘向量机相结合,构建螺旋CT电气故障诊断模型。 (5)得到螺旋CT电气故障类型,完成螺旋CT电气故障诊断。 为验证文章方法在进行螺旋CT电气故障诊断中的性能,以B市某三级甲等医院的螺旋CT机为实验对象。选取该院在2020年间螺旋CT机运行记录中的120组数据作为螺旋CT电气故障诊断的数据样本,60组数据为螺旋CT电气故障诊断的测试样本,其中共包括13种故障类型。 表1为应用文章方法与文献[2]、文献[3]方法分别对含有不同螺旋CT电气故障的CT电气故障诊断数据样本进行螺旋CT电气故障诊断得到的螺旋CT电气故障诊断结果与实际的螺旋CT电气故障识别组数对比表。由表1可知,应用文章方法进行螺旋CT电气故障诊断时得到的诊断结果与实际故障类别组数基本一致,只有在检查程序故障、DAS数据变换故障的诊断结果中,出现了诊断组别个数与实际结果不一致的状况,而另外两种方法难以准确将所有组别的故障类型诊断出来,特别是文献[3]方法的螺旋CT电气故障识别结果最差。由此说明应用文章方法可有效诊断螺旋CT电气故障,更好地满足实际螺旋CT电气故障诊断需求,并且诊断的可靠性较高,误差较低。 表1 螺旋CT电气故障诊断识别组数结果对比表 为验证应用文章方法在进行螺旋CT电气故障诊断时的准确性,分别使用核函数优化前的最小二乘支持向量机与核函数优化后的最小二乘支持向量机对50个螺旋CT电气故障诊断预测样本进行故障诊断分类预测,并将其与实际的测试集故障诊断分类结果进行对比,得到的对比图如图3。在图2中,核函数优化前得到的测试集分类结果与实际测试集分类结果相比,有4项与实际测试集分类不符,对测试集进行正确分类的准确率为60%,对核函数进行优化后得到的测试集分类结果中,只有1项与实际测试集分类结果不符,准确率高达90%。实验说明:应用文章方法进行螺旋CT电气故障诊断具有较高的故障诊断准确率,故障诊断性能良好。 (a)核函数优化前分类效果 为验证应用文章方法进行螺旋CT电气故障诊断时参数优化性能的优劣,绘制应用基本粒子群算法进行参数优化与应用改进粒子群算法进行参数优化时在不同进化代数下的适应度曲线,结果如图4。分析图4可知,应用基本粒子群算法对最小二乘向量机进行参数优化得到的适应度曲线,在约前100次的进化周期内,曲线波动较明显,在此之后曲线呈现平缓状态,参数在此后实现了优化。而应用改进粒子群算法对最小二乘向量机进行参数优化得到的适应度曲线,在约前50次的进化周期内,曲线波动较明显,在此之后曲线呈现平缓状态。实验证明:应用改进粒子群算法在较短的进化周期内便可实现参数优化,在进行参数优化方面的优势更明显,文章方法应用改进粒子群算法进行参数优化后,可使螺旋CT电气故障诊断的效率得到提升,更好满足螺旋CT电气故障诊断需要。 图4 参数优化适应度曲线 交叉验证率是反映螺旋CT电气故障诊断准确率的重要指标。图5是应用文章方法与文献[2]方法、文献[3]方法在进行螺旋CT电气故障诊断时得到交叉验证率。由图5可知,文献[2]方法的最高正确率与平均正确率为85%与80%,文献[3]方法的最高正确率与平均正确率仅为65%与55%;而应用文章方法的最高正确率与平均正确率可达95%与90%。实验说明:应用文章方法进行螺旋CT电气故障诊断时的交叉验证正确率更高,在对螺旋CT电气故障进行诊断时更具优势。 图5 不同方法螺旋CT电气故障诊断交叉验证率 应用文章方法可有效诊断螺旋CT电气故障,满足实际螺旋CT电气故障诊断需要。但该方法在进行螺旋CT电气故障诊断时,尽管迭代能力很强,但在每一次迭代时的运算时间却相应地有所增加。下一阶段将会对如何在诊断CT电气故障时,通过降低每一次迭代时的运算复杂度,进一步提高螺旋CT的故障诊断效率的方法进行研究。2实验与分析
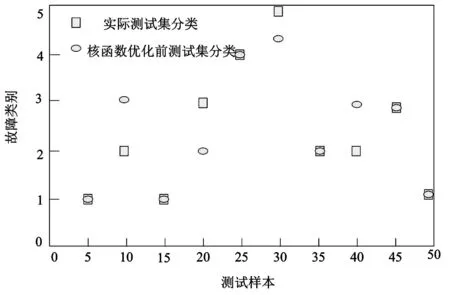
3结语

