回焊炉炉温曲线设计与优化

罗皓洋, 龚海林, 余美奇, 熊静妍

(1.江西师范大学 物理与通信电子学院,南昌 330022; 2.江西师范大学 数学与统计学院,南昌 330022; 3.江西师范大学 国际教育学院,南昌 330022)

0 引 言

在电子产品生产过程中,将电子元件自动焊接至电路板上的方式是将电路板放置在回焊炉中加热.生产过程中为保证较高产品质量,需要回焊炉的各部分保持工艺要求的温度.目前,该领域相关工作需要通过实验测试来进行控制和调整,本文以2020年“高教杯”全国大学生数学建模竞赛A题“炉温曲线”为例进行研究[1].

该赛题设定了生产工艺中的一些参数条件(具体内容可参见文献[1]),要求参赛选手得出对应的炉温曲线,并进行优化研究.根据全国大学生数学建模竞赛组委会发布的优秀论文展示[2]:编号A195的文章对炉温曲线的优化采用双目标非线性规划进行求解,考虑了不同目标的优先级,改进了规划求解算法.但忽略了热辐射对炉温曲线的影响,在刻画峰值温度时容易产生偏差.编号A212的文章采用了多重搜索法与模拟退火算法进行求解,避免搜索结果陷入局部最优.虽然降低了一定的运算量,但是所采用模拟退火算法耗时较长,所得最优解存在较大误差.编号A147的文章在对炉温曲线优化求解时,采用了爬山、A*等人工智能算法,使得结果更加精确,但是遍历空间过大,容易导致程序运行缓慢.

本文在充分考虑热辐射对炉温曲线影响的基础上,综合考虑各种传热方式,并设定合理的边界条件,构建了改进的热传导方程,模型求解模拟所得温度分布曲线与根据实验所测数据所得曲线基本重合,拟合优度高,所得模型结果能很好地用于炉内温度分布的预测,为实际生产工作提供了可靠的现实依据.同时,模型求解简单直观,程序运行也较快.

1 非线性瞬态传热数学模型的建立

1.1 基本理论

① 热传递基本方式

在热力学过程中,有三种基本的热传递方式:热传导、热对流和热辐射.

(i) 热传导:因导体内部存在的温差或温度梯度引起自由电子发生移动进而实现热量传递.固、液、气三相均存在此种传热方式.主要以傅里叶定律为依据计算[3].

(ii) 热对流:流体质点因运动发生相对位移而导致热量传递.主要以牛顿冷却定律为依据计算.

(iii) 热辐射:受热物体内部原子振动形成的电磁波能量传递,任何物体均可发生.

② 边界条件

对于导热问题,为确保其具有唯一解,往往需附加一定的边界条件和初始条件,此类问题一般来说有三类边界条件.以T(x,y,z,t)作为温度分布函数,Γ作为物体边界进行以下说明.

(i) 第一类边界条件:规定边界上的温度值为

T(x,y,z,t)|(x,y,z)∈Γ=f(x,y,z,t);

(ii) 第二类边界条件:规定边界上的热流密度为

(iii) 第三类边界条件:规定边界上物体同其相接触流体介质间的对流传热系数与温度为

1.2 模型假设

(i) 假设开始加工时炉内空气稳定;

(ii) 假设传热过程中产生的耗散热忽略不计;

(iii) 假设题目附件中所给的统计数据信息真实可靠;

(iv) 不考虑电子元件材料种类、质量等指标对温度传感器及焊接效率的影响;

(v) 假设温区间隙处温度是恒定的,同时不考虑回焊炉系统内部热源的影响;

(vi) 假设电子元件进入回焊炉的过程中,内部热源的影响可以忽略,y,z方向上各状态参数稳定不变,即只需要考虑电子元件沿传送带运动方向(x方向)上的温度变化.

1.3 模型建立

1.3.1 吸热过程分析

以焊板为研究对象,以其类型下的印制电路板组装件(Printed Circuit Board Assembly, 简称PCBA)为例,分析其吸热过程.在回流焊接过程中,PCBA吸收的热量可由式(1)表示[4]:

QPCBA=mcp(T(t)-T(i)),

(1)

式中,m为组件质量(单位kg),cp为质量定压热容(单位J/(kg·K)).

PCBA在回焊炉中存在三种热量传递方式,分别为:热传导、热对流和热辐射.

对于PCBA,因其在传送导轨上通过时仅吸收极少的热量,所以可以认为热传导过程对其传热影响可忽略不计[5].对其对流与辐射传热两个过程,基于牛顿冷却定律,可由式(2)-(3)表征:

Qc=hcAPCBA(Tair-TPCBA),

(2)

式中,Tair为热风温度(K),TPCBA为PCBA(含元器件)温度(K).

Qr=hcAPCBA(Tair-TPCBA),

(3)

同时,对流传热还受到热风温度、与PCBA的接触面积等因素影响.

1.3.3 PCBA瞬间受热过程分析

对单位时间内的焊接过程,有[6]

QPCBA=Qc+Qe.

(4)

由式(1)～(4)可得

mc(T(t)-T(i))=[hc+hr]APCBA(Tair-TPCBA).

(5)

对于瞬间传热有[7]:

患儿进行内科介入治疗/外科手术前，SPE组成员首先评估患儿及家属的心理状态和应对情况，有针对性地给予围术期健康教育和心理辅导，同时将相关信息及时反馈给介入中心/手术室的责任护士，有利于医务人员更好地从生理、心理和社会等方面连续性照护患儿。

(6)

变换为积分式:

(7)

1.4 模型求解

1.4.1 参数的选取

对回焊炉系统,建立了单温区炉腔模型,如图1所示.

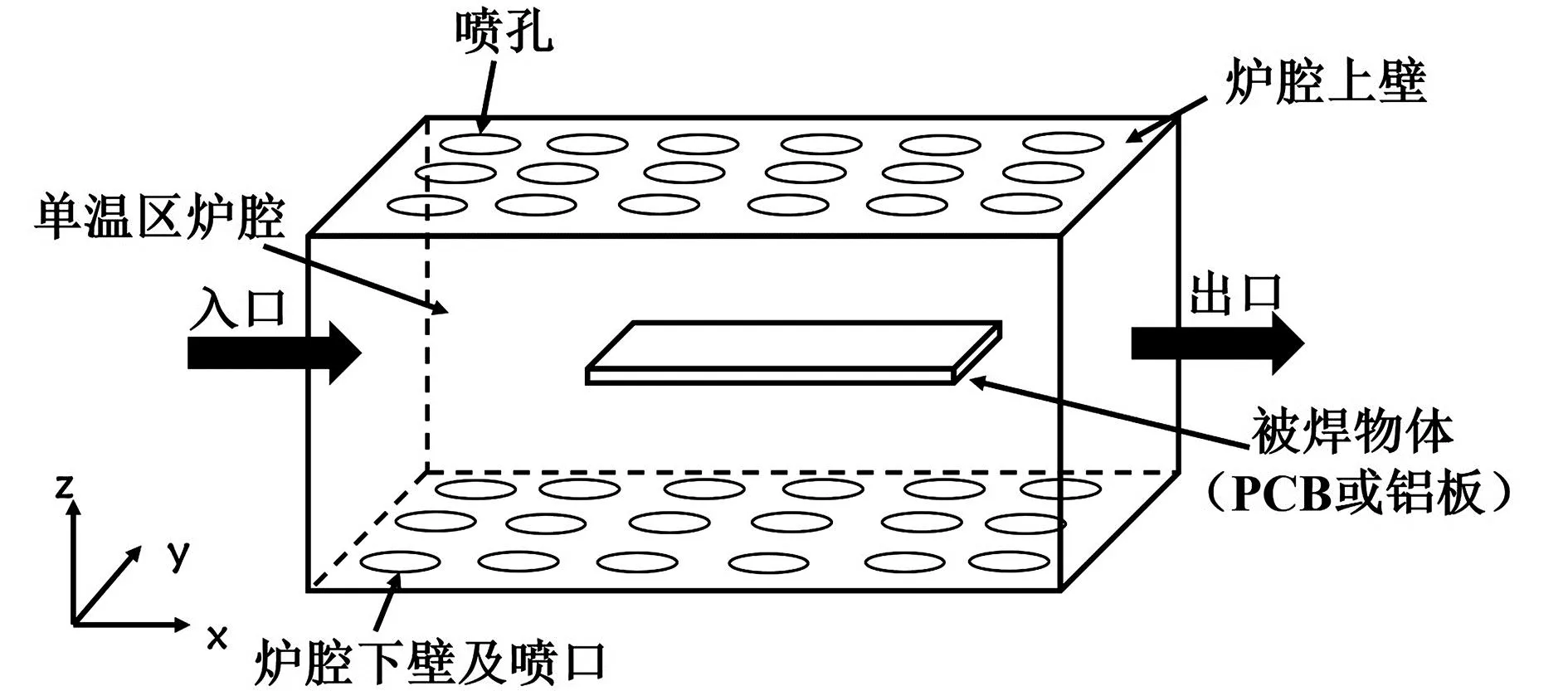
图1 单温区炉腔模型

为不失一般性,分别取单温区长度L=300mm,高度G=2H=200mm,宽度W=300mm,喷孔直径D=10mm,喷孔间距S=50mm,炉腔上下壁具有相同的喷孔分布.以下是参考文献[4-7]后选定的各温区参数计算表.

1.4.2 方程的求解与实现

基于表1中给出的参数计算表,同时对式(6),为利于编程求解,将其转换为差分方程:

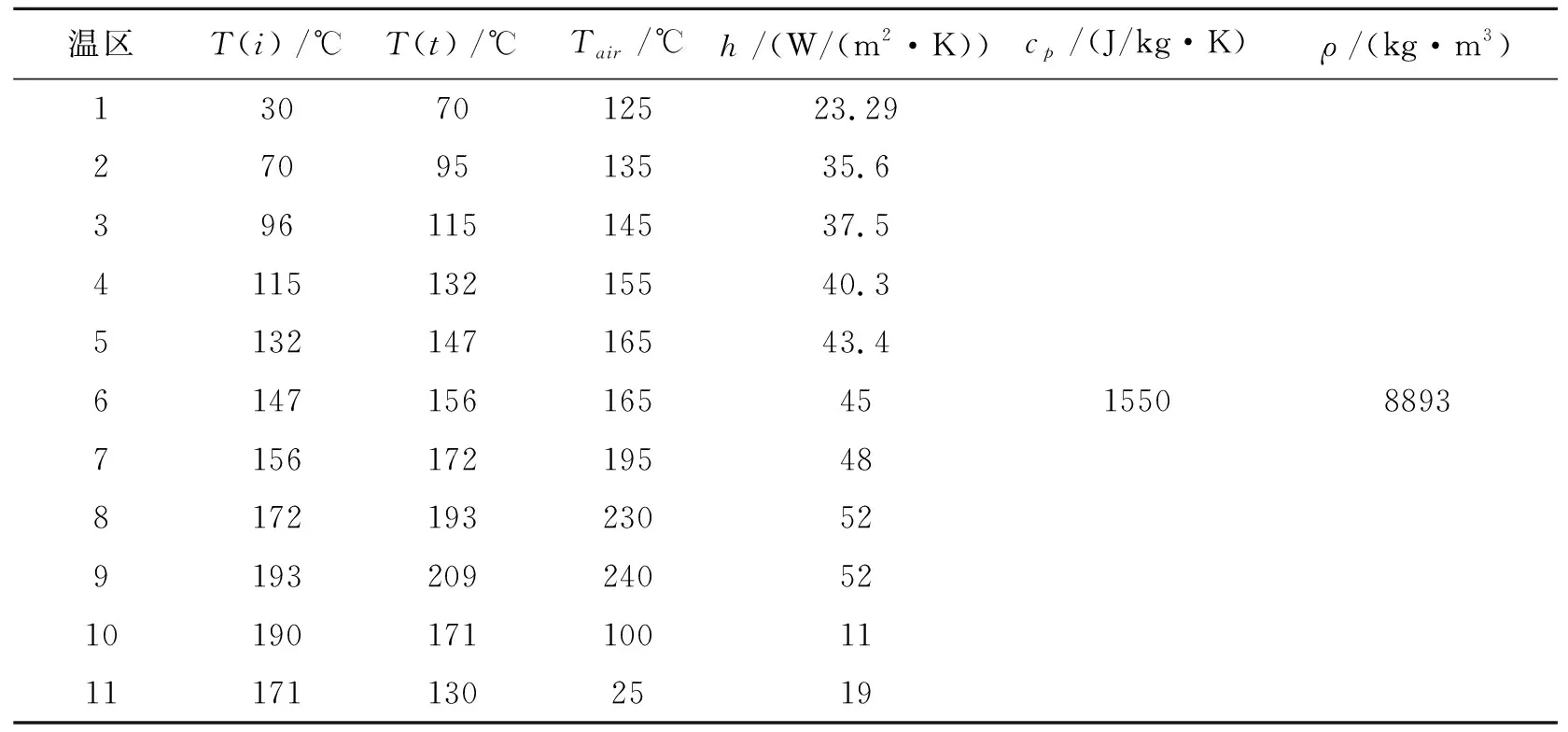
表1 各温区参数计算表

(8)

1.4.3 模型的结果与分析

通过相关参数的选取配合MATLAB的编程实现,得到了以下结果:

t3=66.3462℃,t6=148.2692℃,t7=175.5769℃,t8=214.6154℃.

其中t3,t6,t7,t8分别对应小温区3,6,7中点及小温区8结束处焊接区域中心的温度.同时得到了初步模拟的炉温曲线与不同时间下的温度曲线,如图2所示.

图2 (a) 初步模拟得到的炉温曲线;(b) 温度求解曲线

同时,考虑模型方程中一些参数存在的波动,对此进行了优化并同经实验测得后所绘制的炉温曲线进行比对,如图3所示,发现模拟所得曲线与根据实验所测数据所得曲线基本重合.引入拟合优度R2对模拟结果的拟合效果优劣程度进行定量刻画[8],计算得到R2=0.9056,证明了所建立模型具有较强的合理性与准确性.

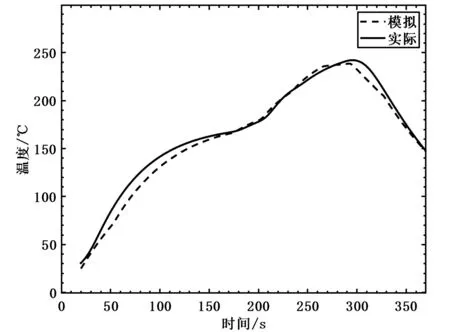
图3 优化模拟得到的炉温曲线

2 传输带速度模型建立

2.1 穷举法的思想

穷举法是通过在可能的解空间中穷举出每一种可能的解,并对每一个可能解进行判断,从中得到问题的答案的一种算法.该算法思想简单,易于实现,在解决一些规模适中的问题而无须过多考虑求解速度时,使用穷举法不失为一种很好的选择.

2.2 模型的限制条件

回焊炉加热过程需要考虑印制电路板(Printed Circuit Board,简称PCB)板材料特性和焊接元器件的耐热性,所以在实际生产中存在诸多的限制条件,见表1[1].

2.3 模型的建立

以最大传送带过炉速度作为优化目标,选取表2中提供的制程界限中的相关参数及回焊炉系统中一般性物理原理的限制作为限制条件,传送带的过炉速度作为控制变量,列出如下模型方程组:

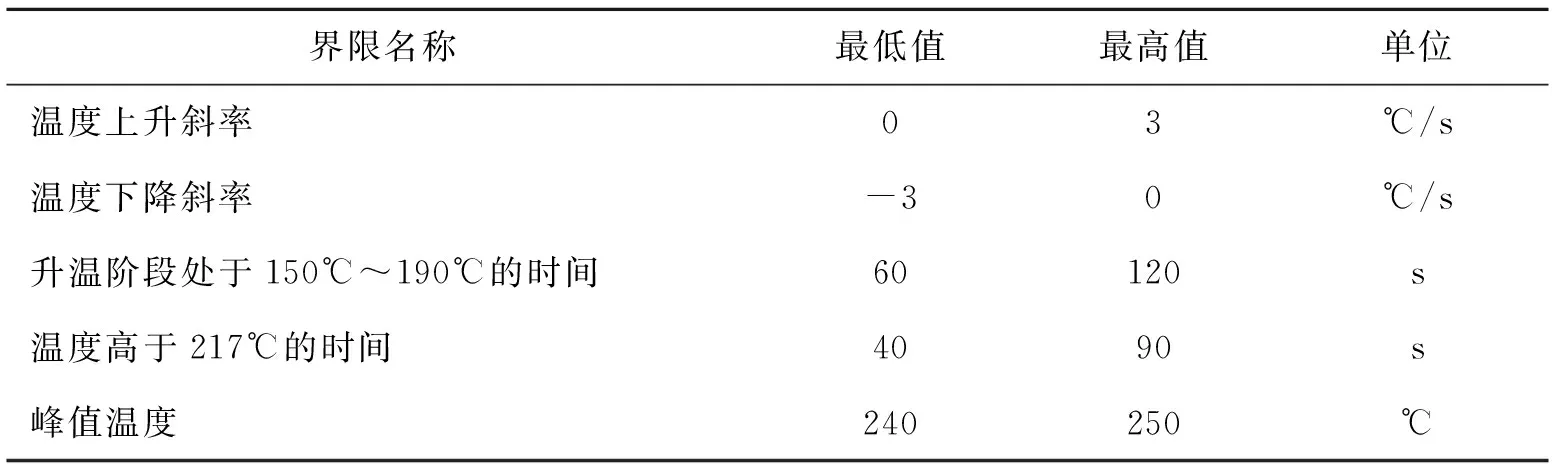
表2 制程界限

(9)

2.4 模型的结果与分析

2.4.1 模型的结果

利用MATLAB编程[9],进行穷举算法,经过多次的循环,得到了基于前文所述条件下的最大传送带过炉速度:

v=69.700cm/min.

(10)

2.4.2 模型的分析

接下来,对构建的优化模型进行灵敏度分析.

根据式(10),对于回焊炉系统,其传送带过炉速度主要由制程界限中的温度限制量决定.下面分析具有时间限制的温度上升区间和峰值温度的区间变动对模型结果的影响.已知温度上升与下降的斜率区间和超值温度时限区间一定,对于峰值温度的区间,选取[217,240]为温度下界变动区间,[250,265]作为温度上界变动区间;对于具有时间限制的温度上升区间,选取[30,150]作为下界的波动区间,[190,217]作为上界的波动区间.通过MATLAB绘制见图4.

(a) 时间限制下的温度上升区间上界变动影响;(b) 时间限制下的温度上升区间下界变动影响;(c) 峰值温度区间上界变动影响;(d) 峰值温度区间下界变动影响图4 峰值温度区间上下界与时间限制下的温度上升区间上下界变动影响

由图4中的(a)-(d),发现二者温度上界稳定,故其均对速度的影响不大;而对于二者下界,其中峰值温度下界在238℃发生突变,时间限制下的温度上升区间下界在102℃发生突变,由此有理由认为,制程界限中温度区间给定是合理的,任意调换温度区间的下界值将会影响实际回流焊接工程中对传送带过炉速度的调控.

3 阴影面积寻优模型的建立

3.1 极限思想

用极限概念分析和解决问题的一种数学思想.其一般步骤可概括为:对于某一未知量,先假设一个同它有关的变量,并且该变量通过无限过程的结果就是所求的未知量,最后利用极限计算来得到这结果.

3.2 模型建立

采取与上述的优化模型类似的思想构建阴影面积寻优模型.选取最小阴影面积作为优化目标,选取表2提供的制程界限中的相关参数及回焊炉系统中一般性物理原理的限制作为限制条件,各温区设定的温度值与传送带速度作为控制变量,建立了如下优化方程组:

(11)

3.3 阴影面积寻优模型求解

对于曲线的阴影面积,理论上可以采用积分进行求解,如图5所示,列式如下:

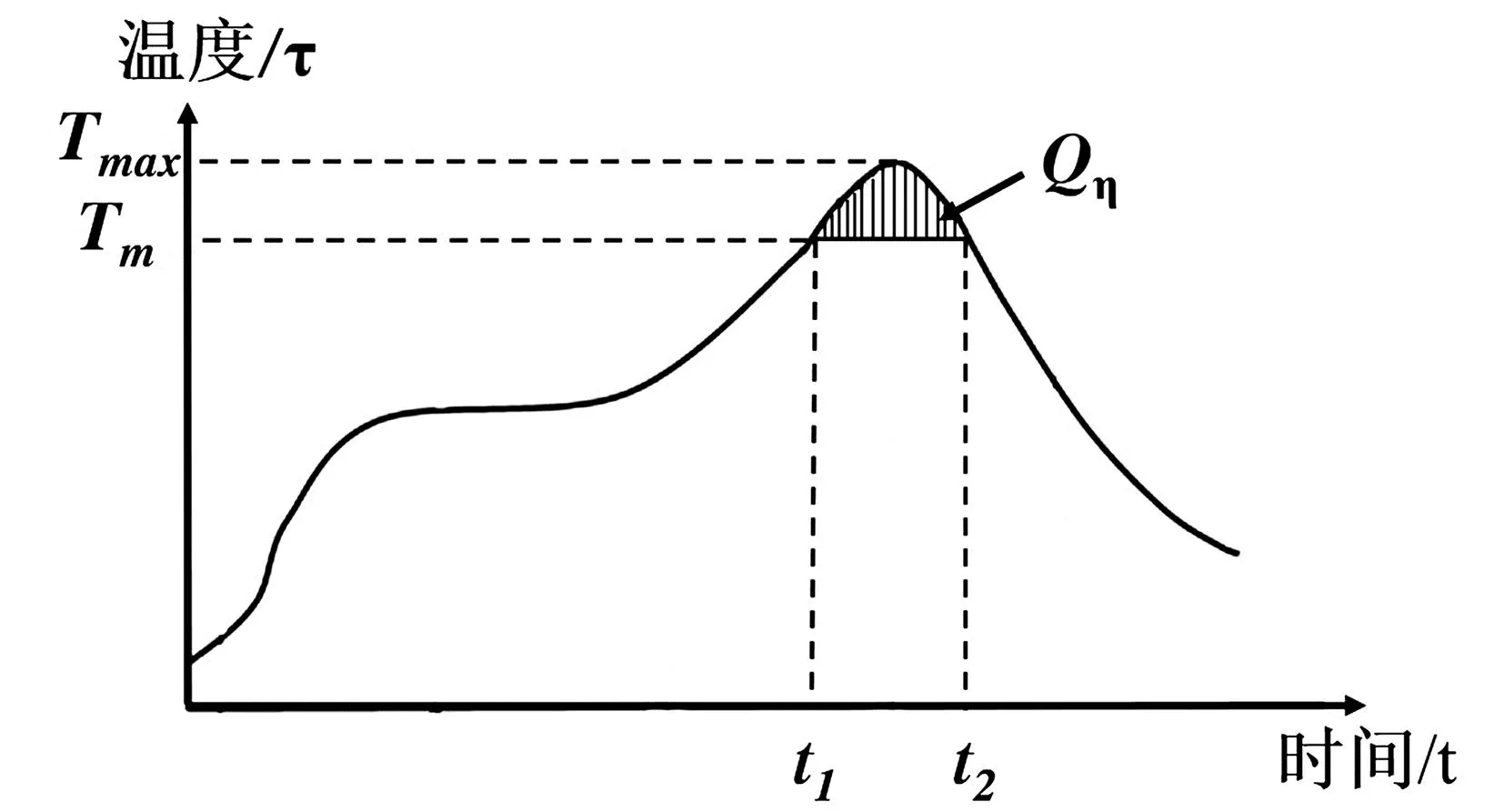
图5 炉温曲线阴影面积求解图示

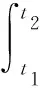
(12)

考虑用一条从t1-t2、高为ΔT的正弦曲线对原曲线进行近似模拟以简化求解,这样一来S就可以简化为

(13)

考虑极限思想,温度曲线的最小值应为一个三角形,由温度大于217℃的时间和峰值温度两个界限,可以求出理论边界值为460,以此值作为下边界对阴影面积进行近似估算,最后通过MATLAB进行仿真,采用双重for循环枚举遍历,得到最优炉温曲线与各温区温度参数及速度同最小阴影面积关系曲线,如图6、图7所示.其中,最优速度为v=93cm/min,最优温度分别为183℃, 185℃, 243℃, 265℃,最小面积为613.6508cm2.

图6 最优炉温曲线

图7 各温区温度参数及速度同最小阴影面积关系

下图展示了各温区温度参数及速度同最小阴影面积关系.由图7可以看出,在恒温7区其同最小阴影面积呈线性上升关系,回流区呈非线性下降关系,速度呈线性下降关系.由此通过逐步定长迭代寻优得到阴影面积最小解.

4 结 论

本文分析了PCB板在回焊炉进行回流焊接过程中的受热情况,使用物理知识对整个过程进行分析,之后结合数学建模思想对PCB板的受热过程进行了模拟,得出结论如下:

(i) 基于传热学原理,结合PCB在回焊炉中加热的实际物理过程,建立了非线性瞬态传热模型,使用有限差分方法完成求解,得到了温度分布及随时间演化曲线,有效取代了针对回焊炉炉温曲线传统研究中仿真困难的问题.

(ii) 根据PCB板经过不同温度的受热情况,结合设备参数,建立了传输带速度和阴影面积寻优模型,实现了对得到的炉温曲线的优化.

(iii) 本文所建立模型旨在为相关领域研究学者提供可能的优选思路,专业科研工作者可以考虑利用ANSYS软件对再流焊各炉区的加载温度进行仿真研究,以获得各组件优化加载温度条件下的动态温度场,进一步验证本文所采用的几何模型和材料参数,同时评估再流焊的仿真的工艺参数是否可以用来指导生产.

致谢非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见!同时,在对本文模型结果进行可视化的过程中,FigureBest插件帮助极大,在此对其创作者致以由衷感谢!