案例剖析问题主导式的假设检验基本概念的教学设计

付芳芳, 许道军, 夏梦雪

(陆军炮兵防空兵学院 基础部,合肥 230031)

0 引 言

本节位于假设检验这一章的第一节,其特点是概念多、内容杂、较抽象、难理解.共涉及8个新概念,传统的授课方式先介绍所有抽象概念再讲解例题,大多数学生会有种囫囵吞枣的感觉,对假设检验的思想和原理还是理解不透彻,只知道有若干公式和程式化的解题步骤,只会生搬硬套,遇到实际问题时却不知道如何利用假设检验进行统计推断.

目前,针对本科生“假设检验基本概念”章节的教学设计能查阅到的文献较少,有的侧重翻转课堂的使用[1],有的侧重思政元素的融入[2],有的侧重部分知识点的探讨[3],文献[4]中也对本节内容进行了重新设计,但没有充分利用离散型案例揭示的检验思想去解决后面的连续型案例,而是继续沿用传统教材的解决方法,没有将前后案例有效衔接,没有将离散型和连续型案例充分联系.本文是在基于学为主体充分体现、思政元素有效融入、前后案例紧密衔接等原则下,提出的案例分析问题主导式的教学设计,力争做到知识传授、能力培养、价值引领三者有机融合.

1 内容设计

1.1 检验思想

上课开始,先提问同学们,香甜可口的奶茶是否都喝过?喝奶茶的时候是否能鉴别出所喝的奶茶是由先倒茶后倒牛奶还是由先倒牛奶后倒茶制作出来的? 进而引入统计学历史故事——女士品茶问题.

引例1Fisher的女士品茶问题:一种饮料由牛奶和茶按照一定比例混合而成,可以先倒茶后倒牛奶(TM)或者反过来(MT).某女士称,她可以鉴别是TM还是MT.

Fisher的试验设计 准备8杯以两种方式冲泡的奶茶,TM和MT各半,把它们随机的排成一列请该女士品尝,并告诉她TM和MT各半,然后请她说出哪4杯是TM,结果她全说对了.

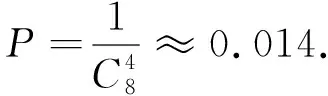
与学生共同分析该案例,由于此试验结果是一个小概率事件,故由小概率原理,得出此试验结果为推翻H0提供了足够充分的证据,因此判定该女士有鉴别能力.

介绍女士品茶试验设计在统计学中的重要意义,带领学生一起提炼Fisher检验方法的基本思想(如图1所示),同时引入概念1原假设H0和备择假设H1.

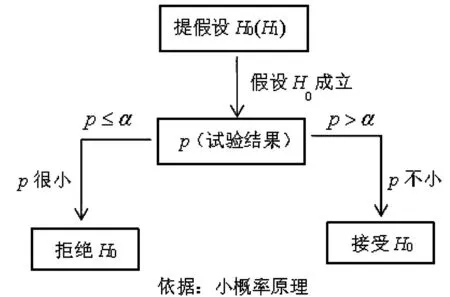
图1 假设检验基本思想分支图

利用Fisher这一实验的设计过程融入思政元素.

课程思政1在生活中要善于发现问题并勤于思考,生活处处皆学问,作为未来的指挥军官,同学们更应具备这种素质.

问题1如果该女士说对三杯,则情况怎样?

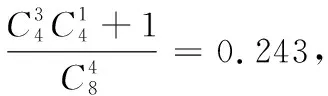
问题2概率到底多小才算是小概率呢?有没有一个衡量标准?进而引入概念2显著性水平α.

问题3指出军事和生活领域的判定问题比女士品茶的复杂之处.提问如何进行假设检验,引入例1,学生通过求解例1理解假设检验的方法步骤.

1.2 检验方法

例1弹药经过长期储存其质量是否会发生变化?现上级主管部门对某后方弹药库中的弹药进行随机抽样检验,共随机抽取9发炮弹进行发射试验,测得数据如下,801,790,798,792,799,797,799,797,801,已知炮弹总体初速X～N(μ,σ2), 根据这些数据能否判断出这批弹炮弹的初速是否符合表定初速800m/s?(给定α=0.05)

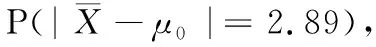
解H0:μ=μ0,H1:μ≠μ0.

若H0成立,

查表得C′=t0.025(8)=2.3060,而P(|t|≥2.306)=0.05,因为2.288<2.306,所以P(|t|≥2.288)>0.05,说明这样的试验结果不构成一个小概率事件,故由图1,接受H0,即根据此次抽样结果判定这批炮弹的初速仍然符合表定初速.

在和学生共同求解例1的过程中引入概念3检验统计量和概念4拒绝域,并融入思政元素.

课程思政2透过现象看本质.

通过例1让学生总结假设检验的方法步骤:提假设,构造小概率事件,选择检验统计量,查表计算,比大小作决策.

虽然例1解决了,但还有更多的细节问题没有考虑,进而请学生分组讨论以下问题.

问题4类似引例和例1这种判决问题在做判决时还有可能犯哪些错误?

问题5假设H0和H1可以调换吗?女士品茶问题中,可以事先假定该女士有鉴别能力吗?炮弹初速检验问题中,可以将炮弹初速不符合表定初速作为原假设H0吗?

问题6例1中的样本均值经过计算为797.11m/s,是小于表定初速的.由于实际中,通常关心的是炮弹经过长期储存,其初速是否会明显降低,所以将问题“是否符合”表定初速修改为“是否小于”表定初速,检验过程会有哪些变化?

第一课时结束,在例1的基础上留给学员问题4和5,引入下一课时的教学内容,两类错误和提假设的原则等其它概念.

1.3 两类错误、提假设的原则

为了解决问题4,先查看学生课前讨论题的回答情况.

课前讨论题无罪推定原则中,在现有证据下,法官作判决时有可能会犯哪些错误?

学生普遍给出以下两类错误,错误1,嫌疑人实际无罪,但法官根据现有证据做出了有罪的判决;错误2,嫌疑人实际有罪,但法官认为现有证据不够充分做出了无罪的判决.

问题7可以同时避免犯这两类错误吗?可以同时降低犯这两类错误发生的可能性吗?在样本容量一定的情况下,能同时降低这两类错误发生的概率吗?

分析 在样本容量一定时,想要降低弃真错误,就会减少拒绝H0而增加接受H0的决策,故又增加了取伪错误.

结论 只能采取一个折中的办法.进而引入概念6奈曼和皮尔逊原则和概念7显著性假设检验.

通过分析奈曼和皮尔逊原则得出H0和H1的地位并不是对等的,H0不能轻易被拒绝,是受保护的,进而引入概念8提假设的原则 .

原则1(弃真后果更严重原则)发生弃真错误所带来的后果远大于发生取伪错误所带来的后果,则将该结论作为原假设H0,其对立面为备择假设H1.例如,防空预警系统中的目标探测问题,H0:“目标存在”;H1:“目标不存在”.2021年新冠病毒感染期间,一旦出现高烧,H0:被感染;H1:未被感染.

原则2(无改变原则)一般将维持现状的结论作为原假设H0,而将改变现状的结论作为备择假设H1.例如,炮弹初速检验问题,H0:初速均值μ=μ0;H1:初速均值μ≠μ0.

概率统计中一般将貌似正确的结论(仅通过计算样本值形成的直观结论)作为备择假设H1,其对立面为原假设H0,并融入思政元素.

课程思政3有时眼见不一定为实,需要进一步验证.

解决了问题4,再利用以上知识详细讲解问题5和问题6.

问题5解答女士品茶问题中,正常人是无鉴别能力,故依据无改变原则,应将“无鉴别能力”作为原假设H0. 炮弹初速检验问题中,由于炮弹初速原本是符合表定初速的,故依据无改变原则,将“符合表定初速”作为原假设H0.

问题6解答H0:μ≥μ0,H1:μ<μ0.

而P{t≤-t0.05(8)}=0.05,查表得-t0.05(8)=-1.86,因为-2.288<-1.86,所以P{t≤-2.288}<0.05,故由图1,拒绝H0,即根据此次抽样结果判定这批炮弹的实际初速是小于表定初速的.

课程思政4仅仅是两个字的不同,但结论截然不同,所以对待问题一定要有一个科学严谨的态度.

课后思考题1为何问法不同,结论截然不同,引起这一不同的原因是什么?这给了在用假设检验作判决时哪些启示?

课后思考题2例1中的两种不同问法,它们的求解过程有哪些共同点与不同点?

2 教学效果评价

课程组成员在对2020级15个教学班学情分析的基础上,选取了6个学情相当的教学班进行课堂教学随堂测试,其中3个教学班采用传统设计教学,3个教学班采用本设计教学.针对学生在知识点的基本理解、简单运用、综合分析三个认知层次共设计了10道题,根据爱课堂平台反馈的数据,将测试结果分别统计到表1和表2中,其中定义掌握程度=平均答题率×平均正确率[7].

表1 传统设计讲解随堂测试结果统计

表2 本设计讲解随堂测试结果统计

对于本设计还在3个教学班共195人进行了问卷调查(见表3),满意度分布如图2所示,学生的评价和建议见表4,听课的校级督导专家、教研室同行也给出了很高的评价,在基础部共126名教员中教学评价综合排名始终位于部系前10名,学习效果和学员评教得分均位于数学教研室共32名教员中前列,见表5.

表3 调查问卷

表4 随机抽取部分学生评价及建议

表5 2020和2021学院教学评价结果

案例剖析问题主导式的教学设计是学院进行课程体系化改造中的重要一项,以此为基础的实际课堂教学竞赛在2021年6月的首届全国数学课程创新示范交流活动中获得军队赛区第二名,在2021年10月的陆军教坛之星教学比武中获得陆军第四名,2022年1月全国职业院校技能大赛教学能力比赛中获全国三等奖.

3 结 论

整个教学设计主要在以下两个方面进行了有效尝试并取得了良好的教学效果:(i)以案例分析为主线,提炼知识点.精选军事案例、层层剖析,注重启发引导、强化知识生成,使教学过程更加符合学生认知规律.(ii)以思维创新为导向,设计问题链.在导入新课、讲授新课及新课小结时均设置了相关问题,引导学生思考、探究,成为分析问题、解决问题的主角,有效提升他们的思维创新能力.

案例剖析问题主导式的教学设计,可以帮助学生提高对实际问题的分析探究能力,对思想方法的总结归纳能力,和对抽象概念的类比简化能力.融入的课程思政元素能够瞄准军事问题,帮助学生增强学习动力,体验数学之重,同时通过探索数据规律,帮助学生强化理性决策,感受数学之威.

致谢特别感谢陆军炮兵防空兵学院王金山教授给出的设计思路,以及与丁玲、张云帆教员的有益讨论,同时非常感谢审稿专家提出的宝贵意见以及参考文献对本文工作的启发.