意愿调查设计导致离散选择模型参数估计偏差的实证分析

陈 林,黄奕慧

(1.蜀道投资集团有限责任公司,四川 成都 610000;2.西南交通大学交通与物流学院,四川 成都 610000)

研究意愿调查问卷的目的就是希望通过科学的实验设计方法设计精细的选择情景,获取出行者意愿偏好数据,进而预测出行者的交通选择行为。常用的实验设计方法包括随机部分因子设计法、正交设计法(Orthogonal Design,OD)以及D-efficient(D-e)设计法。随机部分因子设计法是从全因子组合中随机挑选部分实验组合作为调查问卷内容,该方法能够有效减少实验组合数量,但是该方法无法避免选择枝属性之间存在相关性,一旦相关性达到一定程度将会导致模型参数估计误差[1]。正交设计法以选择枝属性相互正交为准则挑选实验组合,从而避免由于属性间的相关性造成模型参数估计误差。正交设计法由于受到正交性的约束,一旦选择枝属性与属性水平设置过多,采用正交设计法得到的实验组合数量也非常大,这样造成调查工作量与投入非常大[1]。D-efficient设计法以Logit模型渐进协方差矩阵行列式值最小为目标反推实验组合,该方法能够降低模型参数估计的标准差,提高模型参数估计结果的显著度[2-5]。这些实验设计方法具有不同的理论基础且各具优势与不足,在实证研究中有着丰富的应用[6-9]。

理论上无论采用何种实验设计方法,都能得到无偏的模型参数估计结果。事实上,基于不同实验设计方法得到的模型参数结果存在一定程度的差异,尤其是在小样本量情况下。一些学者推测造成此结果的原因是调查问卷存在含有主导项的选择情景[10-13]。主导项是指选择情景中存在某个选择枝的属性水平都优于其他选择枝[5]。一旦选择情景中存在明显的主导项,主导项被选择的概率将远大于情景内的其他选择枝,该情景将无法有效捕捉出行者决策过程中的意愿偏好信息,从而导致模型参数估计结果产生偏差[11-12]。采用效用均衡法检测调查问卷中是否存在包含主导项的选择情景,标定Nested Logit Trick(NLT)模型,对比分析不同效用均衡值的两种实验设计法对效用函数误差项方差、尺度参数与参数估计结果的影响,进而证明是否由于主导项的存在引起误差项方差变化,从而导致模型参数估计结果产生偏差。

1 效用均衡法

效用均衡主要应用于经济学领域,它要求调查问卷的选择情景中每个选择枝具备相似的效用或者选择概率[14]。若选择情景中存在主导项,则主导项被选择的概率将远大于情景内的其他选择枝,那么该选择情景的效用均衡值将较小。效用均衡值通常采用百分比作为衡量标准,某一选择情景的效用均衡值的计算方式,如公式(1)所示[14]

(1)

式中:BS为选择情景S的效用均衡值;J为选择枝数量;PjS为选择情景S中选择枝j被选择的概率。

若调查问卷中存在多个选择情景,则全部选择情景的效用均衡值如公式(2)所示。

(2)

式中:BS为选择情景S的效用均衡值;s为选择情景数量。

2 误差项方差与尺度参数

根据随机效用理论,效用函数U分为可以观测的固定项V和不可观测的误差项ε,并假设它们呈线性关系[1]。因此,交通方式i对出行者n的效用函数可以表示为

Uni=Vni+εni

(3)

Logit模型中,εni独立同Gamble分布时,其概率分布函数和概率密度函数分别为

F(y)=exp[-exp(-λy)]

f(y)=λF(y)exp(-by)]

(4)

式中:λ>0为尺度参数,尺度参数λ的平方与误差项方差D(ε)呈反比的关系,如公式(5)所示:

(5)

根据随机效用理论,出行者n选择交通方式i的选择概率为

(6)

式中:Cn为选择枝集合;Xnjk为选择枝j中的属性k;θk为未知参数;λ为尺度参数。

实证研究中,用极大似然函数法得到未知参数λθk的值,将λ标准化为1(即误差项方差D(ε)=π2/6),从而得到θk的值。根据公式(5),尺度参数的平方与效用函数误差项方差呈现倒数关系。如果误差项方差发生变化,则尺度参数的大小也会发生变化,最终模型参数估计值λθk与真实值θk将存在显著差异。

应用NLT模型,分析不同实验设计法对误差项方差、尺度参数与参数估计结果影响[1]。NLT模型与NL模型(Nested Logit,NL)模型的区别在于层次结构树的划分原理。NL模型将具有相关性的选择枝划分到同一个树枝结构内,而NLT模型则可以按照研究者需要来划分层次树枝结构[1],本文将按照实验设计方法的不同来划分层次树枝结构。

3 意愿调查问卷与调查数据说明

3.1 选择枝属性与属性水平定义

以成都市主城区与卫星城龙泉驿区之间的新增地铁为研究背景,开展意愿调查获取出行者在新增地铁方式情况下交通方式选择行为偏好。通道内的选择枝集合包含地铁、地面公交、出租车、私家车以及客运大巴;选择枝属性包括到站时间、候车时间、费用、车内时间以及下车到目的地时间。选择枝属性水平是在现状水平的基础上相应地增加或者减少相同比例得到[1],如表1所示。

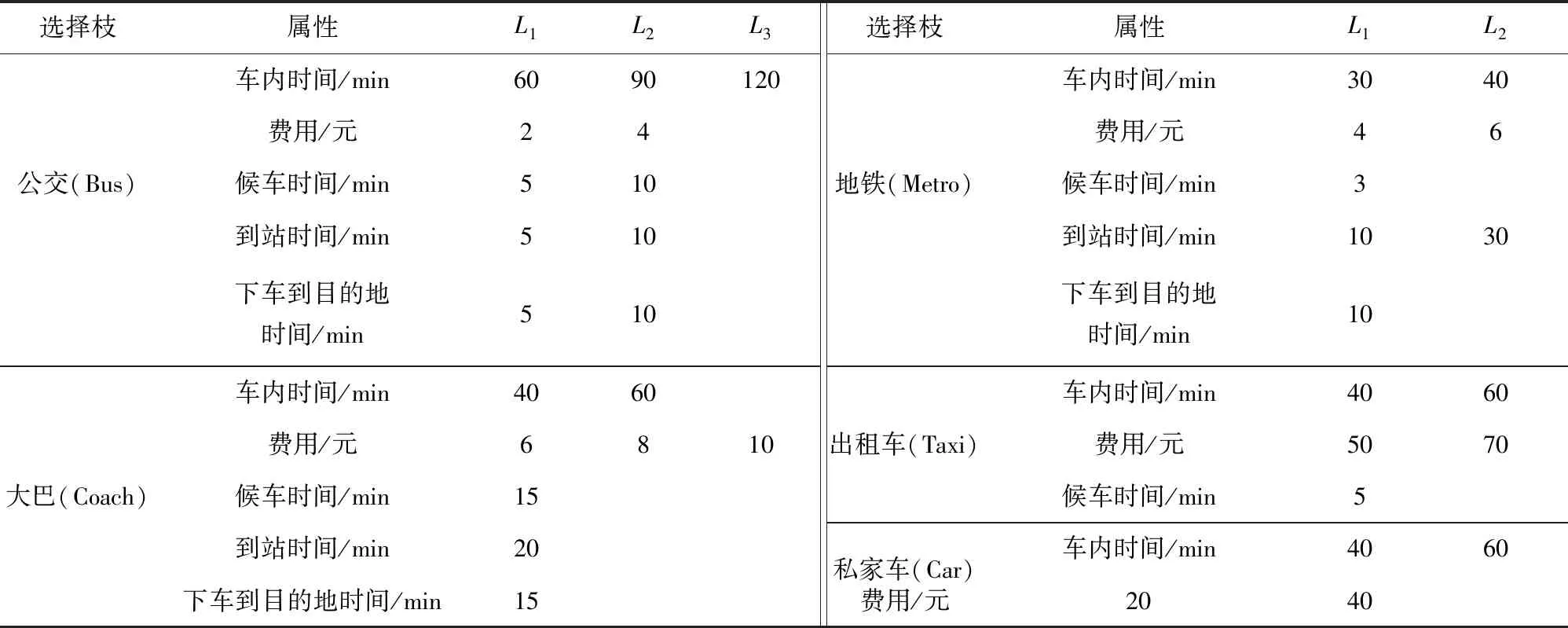
表1 选择枝属性水平定义

3.2 基于正交设计法的意愿调查问卷

按照表1所示的选择枝属性及属性水平,得到全因子组合648个。采用正交设计法挑选属性水平相互正交的组合,最终得到32个组合。正交实验设计法受到正交性条件的限制,不能够按照研究需要确定实验组合数量。所以,将32个组合全部纳入到意愿调查问卷中。为了减轻被调查者的工作量,采用分块实验设计法(Blocking Experiment)在保证正交性的前提下,将32个组合划分为8组,一个被调查者随机完成其中1组。最后,辅助以调查说明、填写说明、选择枝组合相关问题以及被调查者个人属性,形成完整的正交意愿调查问卷。一式完整的调查问卷中包含了8份问卷。

3.3 基于D-efficient的意愿调查问卷

D-efficient实验设计法是以模型渐进协方差矩阵行列式值最小为目标,降低模型参数估计的标准差,获得更加显著的模型参数估计结果[5,10,11]。通常,模型渐进协方差矩阵行列式值采用D-error来表示,D-efficient设计法的数学推导式如下

D-error=det(Ω)1/K

(8)

式中:Ω为离散选择模型的渐进协方差矩阵;K为模型参数估计个数。

渐进协方差矩阵等于费歇尔信息矩阵的逆矩阵,如公式(9)

Ω=I-1

(9)

式中:I为费歇尔信息矩阵。

费歇尔信息矩阵的计算方法,如下公式(10)所示

(10)

式中:L(x,β)为离散选择模型的极大似然函数;Xnjk代表选择枝j的第k个属性;βjk代表选择枝j的第k个属性在效用函数中未知参数。

离散选择模型的极大似然函数,如公式(11)所示

(11)

式中:yni表示决策者n的选择结果;Pni表示决策者n的选择选择枝i的概率。

首先实施预调查采集数据,标定MNL模型,将参数标定结果作为D-efficient实验设计法的参数预先值,如表2所示。得到预先值后,根据上述原理完成实验组合设计。为了同正交设计法进行对比,将实验组合数量设置为32个,最终得到D-error值最小情况下的32个组合方案。同样,为了减轻被调查者的工作量,也采用分块实验设计法(Blocking Experiment)将32个组合划分到8组,一个被调查者随机完成其中1组。最后,将这些组合分别辅助以调查说明、填写说明以及被调查者个人属性问题,形成完整的D-efficient意愿调查问卷,一式完整的调查问卷中包含了8份问卷。

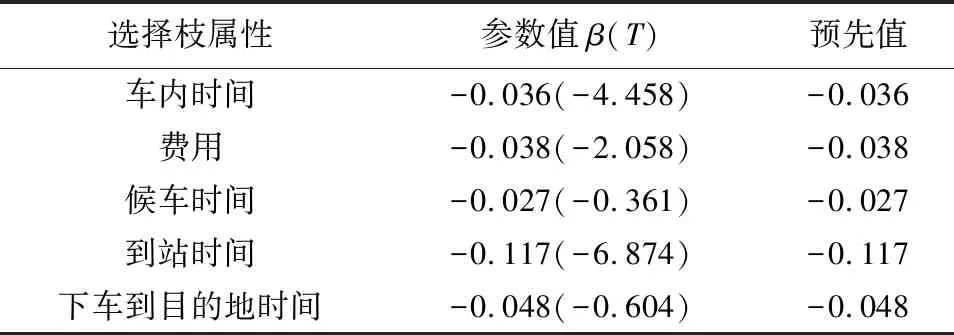
表2 选择枝属性参数预先值

3.4 调查数据分析

所有的问卷调查都采用面对面访问式的调查方式。调查获取出行者在不同选择情景下的偏好数据,同时被调查者还需要提供年龄、收入、性别等个人信息,最终分别得到1 272组有效数据。调查问卷通过设置了4个年龄区间来衡量调查样本的年龄情况,同样设置了5个收入区间来呈现被调查者的收入分布情况,每种问卷对应调查样本的总体属性统计情况如表3所示。根据表3可以看出,两组调查样本的总体特征基本符合该城市人口的总体特征,两组调查样本的总体特征之间不存在显著差异,说明调查样本的总体特征不会对模型参数估计结果存在显著的影响。

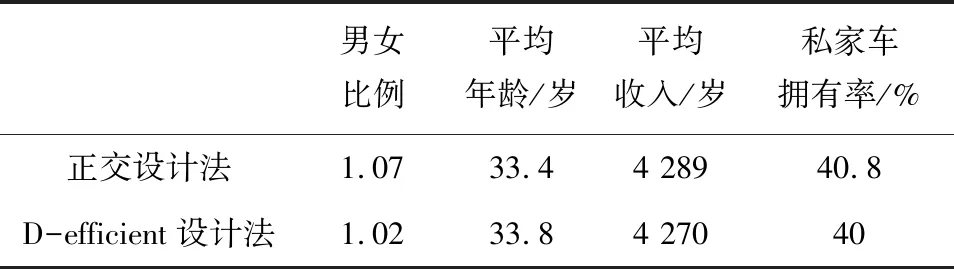
表3 调查样本总体特征表

4 实证结果分析

NLT模型与MNL模型的参数标定结果如表4所示。模型参数结果符号正确且显著,模型拟合度较好。对比两组MNL模型结果发现,两者存在明显的差异,尤其是费用与到站时间等变量,表明不同实验设计方法会导致参数估计偏差。

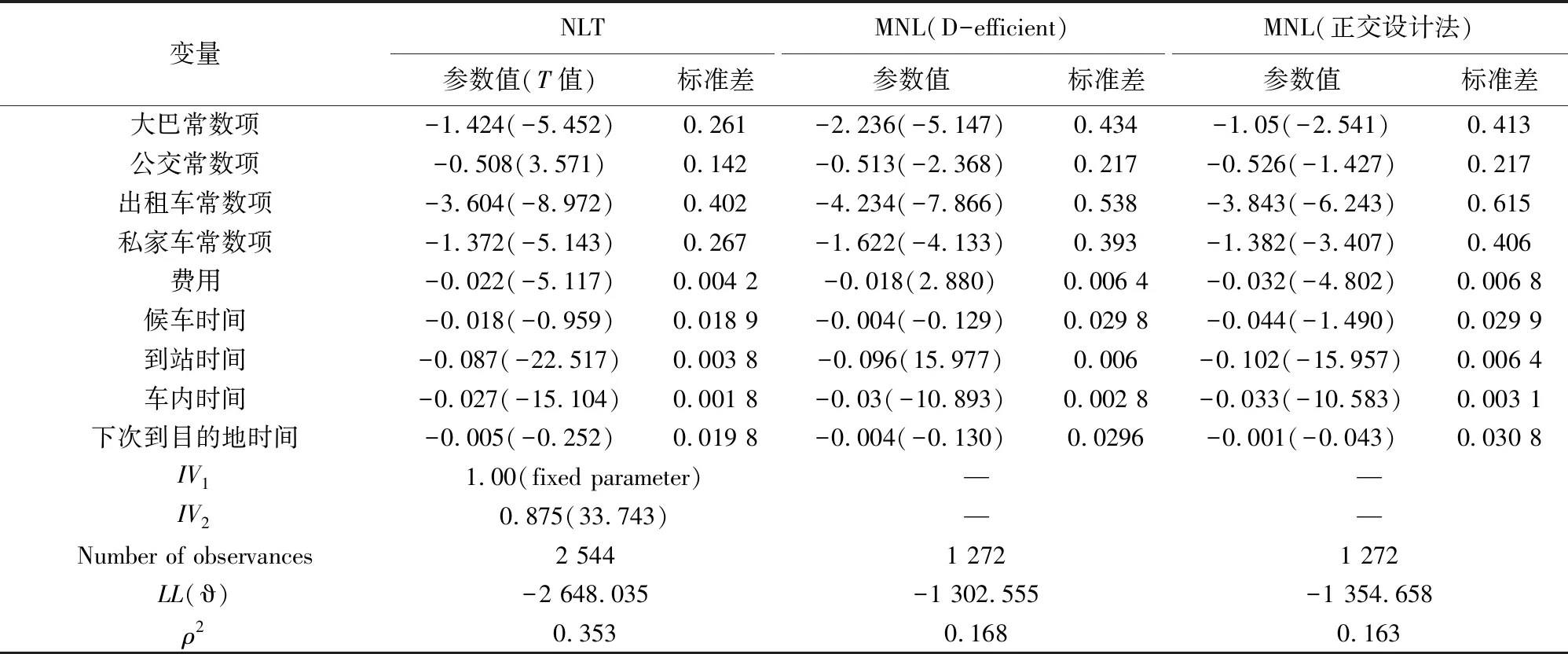
表4 不同实验设计法的模型结果

NLT模型中按照实验设计法的不同划为两个结构树,如图1所示。不同树枝结构间选择枝效用函数误差项相互独立,并且每个树枝结构都有对应的IV参数(IV1,IV2)。IV参数与尺度参数的关系,如公式(12)所示

(12)

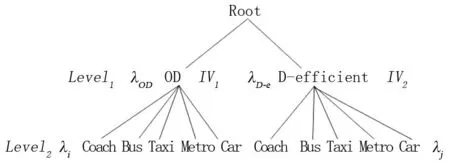
图1 NLT模型的层次结构划分

式中:λOD表示树枝结构OD内Level1层的尺度参数;λi表示树枝结构OD内Level2层的尺度参数。

为了验证基于不同实验设计法得到的模型结果中,效用函数误差项方差是否存在显著差异。将Level1层中的尺度参数标准化为1,即λOD=λD-e=1。如表4所示,NLT模型结果中IV值显著(|T|=33.7>1.96),表明基于两种实验设计法的尺度参数存在显著差异。

根据公式(12)计算得到Level2中尺度参数(λi,λj)的值分别为1与1.14。同时,利用公式(1)、(2)以及(5)计算得到两组调查问卷的效用均衡值以及误差项方差,如表5所示。计算结果表明正交设计法与D-efficient设计法都没有保持良好的效用均衡,即调查问卷中存在一些包含主导项的选择情景。

表5 误差项方差与尺度参数值

根据表5所示,相比于正交设计法,D-efficient设计法的效用均衡值(9.1%)更小,误差项方差更小,尺度参数值更大。表明D-efficient调查问卷中含有主导项的选择情景数量更多,导致其效用均衡值较小。由于主导项的存在,选择情景无法有效获取被调查者决策过程中的意愿偏好信息,造成误差项方差变小,尺度参数值变大,则模型参数估计值(λθk)与真实值(θk)之间的偏差更为显著。

进一步对比了设计D-efficient调查问卷时采用的预先值与MNL模型结果,发现两者间存在明显的差异,表明D-efficient设计法的设计效能有所损失。认为造成D-efficient设计法参数估计偏差大于正交设计法的原因就在于较差的预先值,较差的预先值无法有效的避免选择情景中出现主导项。

5 结 论

分别使用正交设计方法和D-efficient设计法设计了两组出行意愿调查问卷,获取出行者在通道内新增地铁情况下的交通方式选择偏好数据。利用效用均衡法分别计算两组调查问卷的效用均衡值,定量化评估了调查问卷中是否含有主导项的选择情景。根据NLT模型与MNL模型标定结果,对比分析了不同实验设计法对误差项方差、尺度参数以及模型参数估计结果的影响。

(1)通过效用均衡分析发现D-efficient调查问卷的效用均衡值(9.1%)小于正交设计法(11.9%),表明D-efficient调查问卷中存在主导项的选择情景多于正交设计法。NLT模型结果则证实基于D-efficient设计法的效用函数误差项方差比正交设计法小,尺度参数值则更大,模型参数估计值与真实值之间的偏差则更显著。表明由于问卷中存在包含主导项的选择情景,导致效用函数误差项的方差较小,尺度参数值变大,模型参数估计值与真实值之间的偏差更为显著。

(2)D-efficient调查问卷中存在较多包含主导项的选择情景的原因在于较差的预先值,较差的预先值降低了D-efficient设计法的设计效能,无法有效避免选择情景中主导项的存在。

(3)效用均衡在意愿调查问卷实验设计过程将是非常重要的一个过程,它能够有效降低参数估计结果的偏差。