基于ARIMA-Kalman滤波混合算法的铁路进站客流预测方法
郭晓彤,王绮静,劳晶晶,余彦翘,周少婷
(五邑大学,广东 江门 529020)
0 前 言
轨道交通建设的快速发展,使其日益成为新时代旅客的主要出行方式。轨道交通车站客流预测,是优化车站客运组织、提高运营安全和运输效率的有效途径。但车站客流变化会受到诸如天气、季节、节假日等多种因素的随机影响,具有一定的随机性和非线性特征,因此,如何提高客流预测精度具有重要的现实意义。
目前,国内外针对交通客流预测的研究方法主要包括时间序列、灰色模型、神经网络等。赵鹏等[1]针对城市轨道交通进站客流建立ARIMA预测模型。郝勇等[2]以日为单位的客流预测问题建立ARIMA模型;武腾飞等[3]构建ARIMA模型预测公交站上下车客流量。熊杰等[4]用Kalman滤波预测地铁换乘客流。由于上述单一模型在客流预测精度上存在一定误差,部分学者提出混合算法进行改进。李洁等[5]将时间序列与LSTM方法相结合,建立了高铁客流预测的组合模型,并对模型进行了精细调参,此组合模型与其他模型相比,具有更高的预报准确率。王菲华等[6]利用BP神经网络和灰色模型对湖北省公路交通流量进行了预测,预测结果表明,该方法具有较高的精确度。求森[7]采用小波分析法对原始客流数据进行去噪处理后,将时间序列与神经网络相组合后对客流量进行预测,以此提高模型精度。
ARIMA模型机理是对大量的历史数据进行训练后对未来的值进行预测,但由于数据本身易受到外界因素的随机性的影响,预测得到的数据依据会存在误差。Kalman滤波具有的自适应降噪特性,通过对原始数据进行迭代训练,从而达到提高预测精确度的目的。可以发现,在传统ARIMA预测模型中融合Kalman滤波自适应性矫正数据和降噪性能达到有效降低预测误差的效果。但是目前ARIMA-Kalman滤波混合预测算法主要用于产量、网络负载等领域,在城市轨道交通客流预测方面的应用较少。基于此采用ARIMA-Kalman滤波混合算法来预测铁路进站客流,以江门东站实际的进站客流数据为研究样本,通过Python软件建立ARIMA模型,结合自适应Kalman滤波对模型进行修正,得到最优的ARIMA-Kalman滤波混合预测算法,达到提高进站客流预测精确度的目的。
1 模型基本原理
1.1 ARIMA模型
时间序列分析根据系统观测得到的时间序列数据,采用曲线拟合和参数估计的方法来建立数学模型。时间序列分析方法思想主要是利用历史数据对未来数据进行预测。在研究中,时间序列分析法会依据自身的变化规律,利用外推机制来描述时间序列的变化。
在运用时间序列分析法之前要先对数据进行差分平稳化处理、对白噪声进行判断,再进行预测分析。ARIMA模型也叫自回归积分滑动平均模型,该模型由两种模型构成,一种为p阶自回归(AR)模型,其计算方法如公式(1)所示。
Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p+αt,
t∈Z
(1)
式中:φ0,φ1,…,φp(φp≠0)为实数;p为自回归阶数;Xt为零均值平稳序列;αt为随机误差项,为白噪声。
另一种为q阶滑动平均(MA)模型的公式,定义如公式(2)所示,此方程的单变量时序数据(yt,t=1,2,3,…)一般满足下面的关系
Xt=αt-θ1αt-1-…-θqαt-q
(2)
式中:θ1,θ2,…,θq(θq≠0)为移动平均系数;q为移动平均阶数;αt为随机误差项,为白噪声。
ARIMA模型的预测公式如公式(3)所示。
Xt=φ0+φ1Xt-1+…+φp(t)Xt-p+
αt-θ1αt-1-…-θqαt-q
(3)
式中:φ0,φ1,…,φp(φp≠0)为自回归系数;p为自回归阶数;q为移动平均阶数;θ1,θ2,…,θq(θq≠0)为移动平均系数;αt为随机误差项,为白噪声;Xt为零均值平稳序列。
时间序列预测模型的建立,需要通过不断地调整参数来确定最终的模型。据此,一般需要固定的评价指标来衡量,通常会以AIC、BIC、HQIC来判断建立模型的良好性。常用的AIC准则公式如公式(4)所示,BIC准则公式如公式(5)所示,HQIC准则公式如公式(6)所示。
AIC=2×N-2ln(m)
(4)
BIC=ln(n)×N-2ln(m)
(5)
HQIC=ln[ln(n)]×N-2ln(m)
(6)
式中:N为模型参数个数,个;m为模型的最大似然函数;n为样本容量,个。
时间序列预测模型的方法步骤主要分为四步:模型识别和定阶、参数估计以及模型检验。
1.2 Kalman滤波模型
Kalman滤波在已知测量方程方差的基础上,以最小均方差作为估计准则,通过公式基于前一个数据和对应的协方差来预测后一个数据,根据存在测量噪声的数据,对线性系统的状态方程、观测数据、系统噪声等进行一系列变换,预估动态系统方程,得到最优估计的算法。
Kalman滤波模型主要包括状态方程(7)和预测方程(8)。
Xk+1=AXk+Wk
(7)
Zk=CXk+Vk
(8)
式中:Xk+1为k时刻的状态值;Zk为k时刻的系统测量值;A为状态转移矩阵;Wk为白噪声;C为观测矩阵;Vk为观测噪声。
Kalman滤波模型根据空间状态方程来调整Kalman滤波方程,主要包含有五条基本公式。Kalman滤波的基本思想是:用最小均方差误差作为最优的估计准则。建立模型主要有两个步骤:迭代和预测。
假设引入了一个离散控制过程的系统,一般先用一个线性方程公式(9)来表示,而它的系统观察值公式可以用公式(10)来表示。当要预测某一状态时,假设其状态为k,那么状态方程可以表示为公式(11),预测方程为公式(12)[8]。
X(k)=AX(k-1)+BU(k)+W(k)
(9)
Z(k)=HX(k)+V(k)
(10)
x(k|k-1)=Ax(k-1|k-1)+BU(k)
(11)
P(k|k-1)=AP(k-1|k-1)AT+Q
(12)
式中:A为转移矩阵;B为控制矩阵;X(k)为k时刻的状态向量;Z(k)是k时刻的观测向量;V(k)是观测噪声随机向量;x(k|k-1)为在k-1时刻预测k时刻的进站客流值;x(k-1|k-1)为k-1时刻的进站客流客流值;P为协方差矩阵;Q为观测噪声方程的协方差矩阵;公式(10)为系统的测量值方程;公式(11)是为当前状态的预测值,这是由一矩阵的最优值和控制矩阵共同求得;公式(12)为协方差矩阵;U(k)为k时刻的控制变量。
接着计算此系统的Kalman增益如公式(13)所示,结合实际的测量结果用来修正系统状态方程,如公式(14)所示,误差协方差如公式(15)所示[9]。
K(k)=P(k|k-1)HT
×[H×P(k|k-1)HT+R]-1
(13)
x(k|k)=x(k|k-1)+K(k)×[z(k)-H×
(k|k-1)]
(14)
P(k|k)=[I-K(k)]×P(k|k-1)
(15)
式中:K为Kalman增益矩阵;P为k-l时刻的状态协方差矩阵;H为模型状态矩阵;R为测量噪声的协方矩阵。
Kalman滤波的设计方法便捷,通过计算机编程即可实现。也正是这种便捷性,让Kalman滤波在预测方面得以被广泛使用。另外,它的运用依赖于递归的方法和模型的自适应性,与历史数据无较大的联系。
2 混合预测模型
由于存在天气、日期等因素的影响,预测结果与理想值仍有差距。Kalman滤波运用系统状态进行最优估计,根据自身模型的自适应性对数据进行预测,提高结果的精确度。
因此提出一种ARIMA-Kalman滤波混合算法的预测方法来预测进站客流,先构建ARIMA模型,根据模型参数和Kalman滤波方程,得到混合算法。
假设ARIMA模型写成公式,调整其为矩阵的形式,即
(16)
结合Kalman滤波五个主要公式(9)~公式(15)、状态方程(7)和预测方程(8),得到混合算法的预测进站客流预测方程即公式(17)。
Z=C×X
(17)
式中:Z为观测向量;X为状态向量。
3 实例分析
3.1 实验数据
采用江门东站2019年的进站客流数据对前文所述方法进行实例验证。把2019年全年的进站客流数据作为研究的样本,对数据进行预处理后建立客流时间序列,所建立的客流时间序列如图1所示。
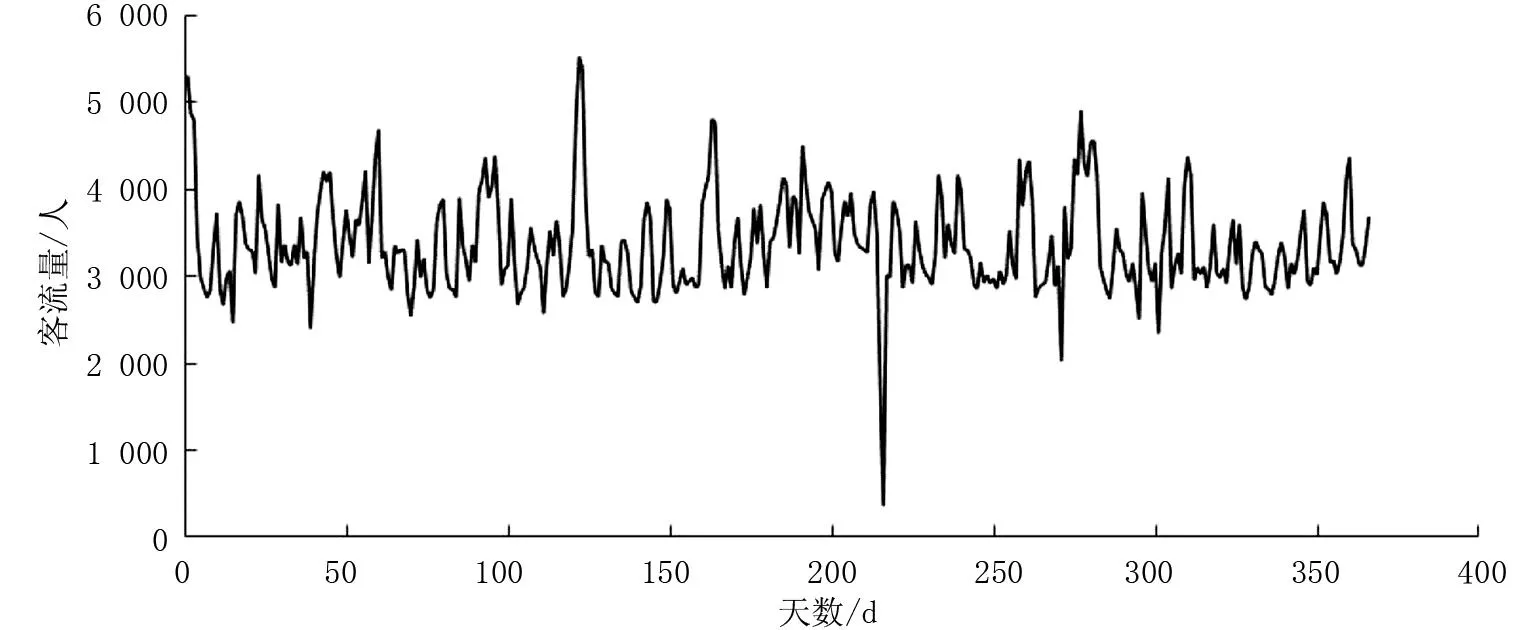
图1 车站原始数据时间序列
对客流数据进行平稳化处理后,确定模型种类和阶数。通过建立ARIMA预测模型,结合Kalman滤波构建状态空间方程,实现用Kalman滤波对客流量进行预测。在此基础上,将江门东站2019年前359 d的数据应用到建立的模型上,预测后7 d的数据;再用前351 d的数据应用到模型上,预测后15 d的数据以及用前331 d的数据应用到模型上,预测后30 d的数据;对比三种预测情况,检验所建立模型的良好性。研究依托大量样本数据,数据支持力度充足,具有一定的可靠性。
3.2 预测性能度量
采用均方根误差(Root Mean Squared Error,RMSE)、平均绝对误差(Mean Absolute Deviation,MAE)和平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)作为客流预测的性能度量指标,它们能反映与实际值的差距,也能反映反映测量的可信程度。因此,利用这三种判断标准来衡量ARIMA模型和ARIMA-Kalman混合算法的良好性。比较预测得到的客流数据与实际的进站客流数据之间的误差,单一算法和混合算法对预测数据的检验提高度,评判标准如下所示。
(18)
(19)
(20)
式中:m为客流预测日期;y为实际客流值;yi为预测得到的客流量。
对所建立的时间序列进行单元根检验。分析检验结果得,P检验值为1.650×10-9小于显著值0.05,说明建立的时间序列是平稳的。因此在本研究中未对数据进行差分处理,即d=0。
为确定模型种类,对客流时间序列前30个自相关系数和偏自相关系数进行计算,结果如图2、图3所示。由图2、图3可以看出,前30个自相关图和偏自相关图都是拖尾的,由此可确定模型为ARIMA(p,d,q)且所建序列是平稳的。
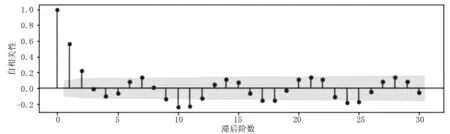
图2 自相关系数
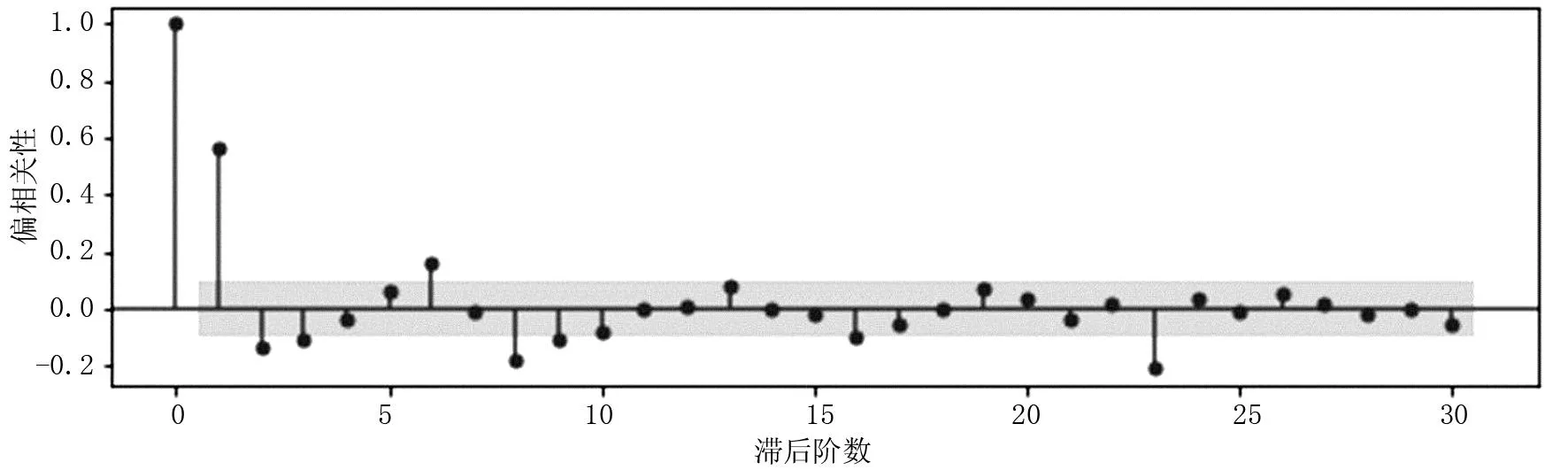
图3 偏自相关系数
仅仅从自相关图和偏自相关图确定模型阶数是比较困难的,所以采用AIC、BIC和HQIC准则来确定模型阶数,定阶结果如表1所示。当p=3,d=0,q=2时,AIC、BIC和HQIC的值皆为最小值,确定模型为ARIMA(3,0,2)。对客流时间序列进行训练,训练结果如图4所示。

表1 模型定阶结果
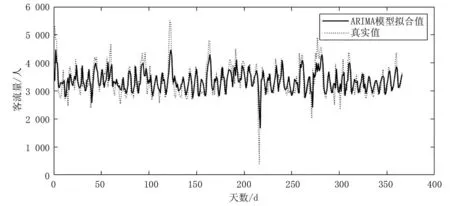
图4 ARIMA模型训练
将建立得到的ARIMA(3,0,2)模型与Kalman滤波结合起来。通过ARIMA-Kalman混合算法对客流量进行预测,得到ARIMA-Kalman模型与ARIMA模型预测结果对比如图5所示。
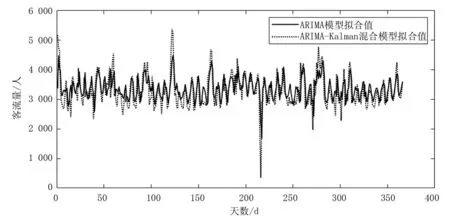
图5 ARIMA-Kalman模型与ARIMA模型对比
ARIMA模型和ARIMA-Kalman模型预测的绝对误差对比图如图6所示。对比图6可得知,ARIMA模型预测得到的进站客流数据误差波动较大、误差值也大,而ARIMA-Kalman混合算法得到的进站客流预测误差波动较小,变化范围基本在0~100左右。相较于ARIMA模型,ARIMA-Kalman滤波混合算法的误差值更小。
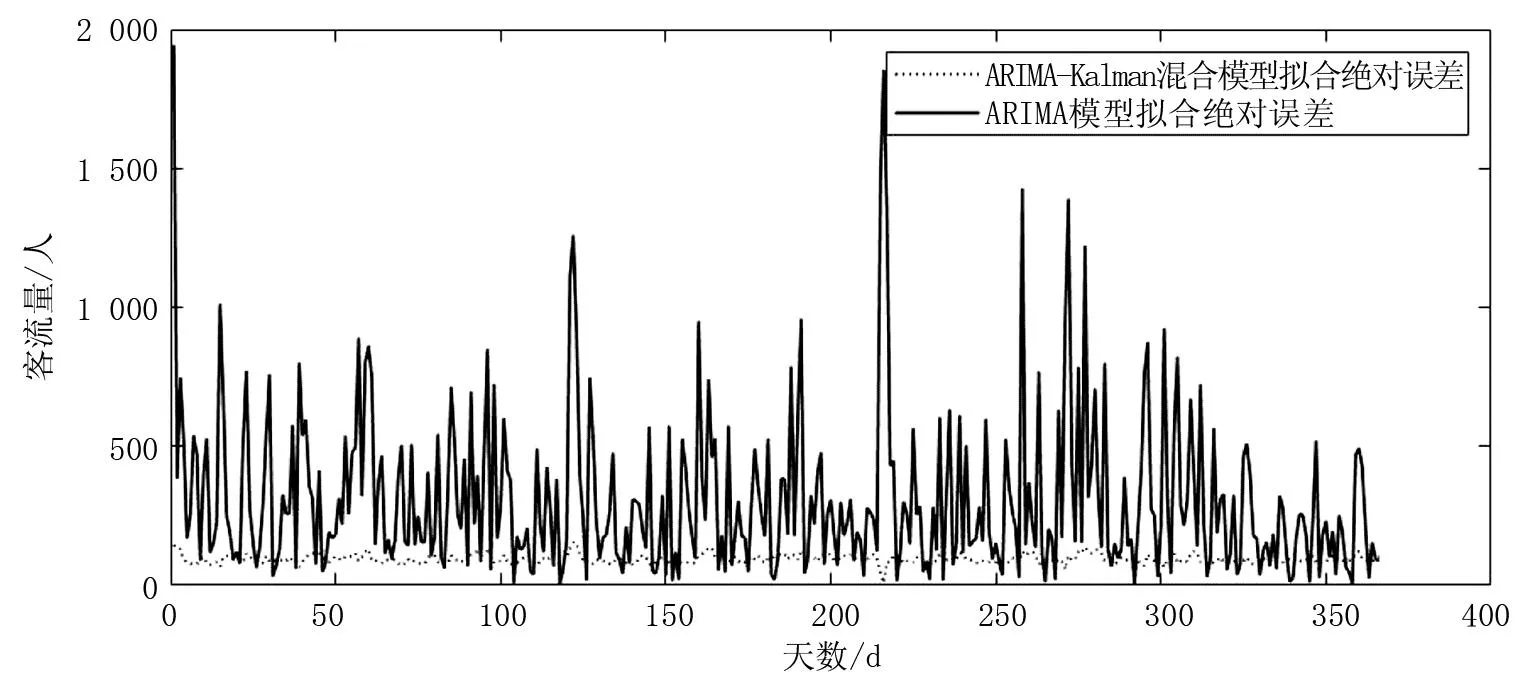
图6 两种模型绝对误差对比
计算ARIMA模型和ARIMA-Kalman模型的预测结果误差,结果如表2所示。其均方根误差由ARIMA模型的425.582下降至ARIMA-Kalman的168.476,降低了257.106;平均绝对误差由ARIMA模型的311.944下降至ARIMA-Kalman的166.269,降低了145.675;平均绝对误差百分比由ARIMA模型的10.610%下降至ARIMA-Kalman的4.955%,降低了5.655%,从表中ARIMA-Kalman混合算法三种误差值均比ARIMA模型要小,证明了混合算法得到的预测值精确度更高。
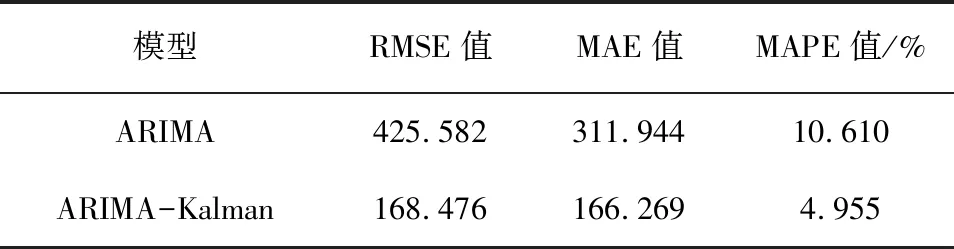
表2 两种模型的误差分析结果
为检验模型建立的良好性,选择江门东站2019年前359 d的数据来运用ARIMA(3,0,2)模型,预测得到未来7 d的进站客流值;选择江门东站2019年前351 d的数据来运用ARIMA(3,0,2)模型,预测未来15 d进站客流值;同理,选择江门东站2019年前336 d的数据来运用ARIMA(3,0,2)模型,预测得到未来30 d的进站客流值,得到的预测结果,如图7所示。可以看出,两种模型预测得到的进站客流变化与实际客流走势基本一致。但相较于单一ARIMA模型,ARIMA-Kalman滤波混合模型预测值更贴近实际值,精确度更优。
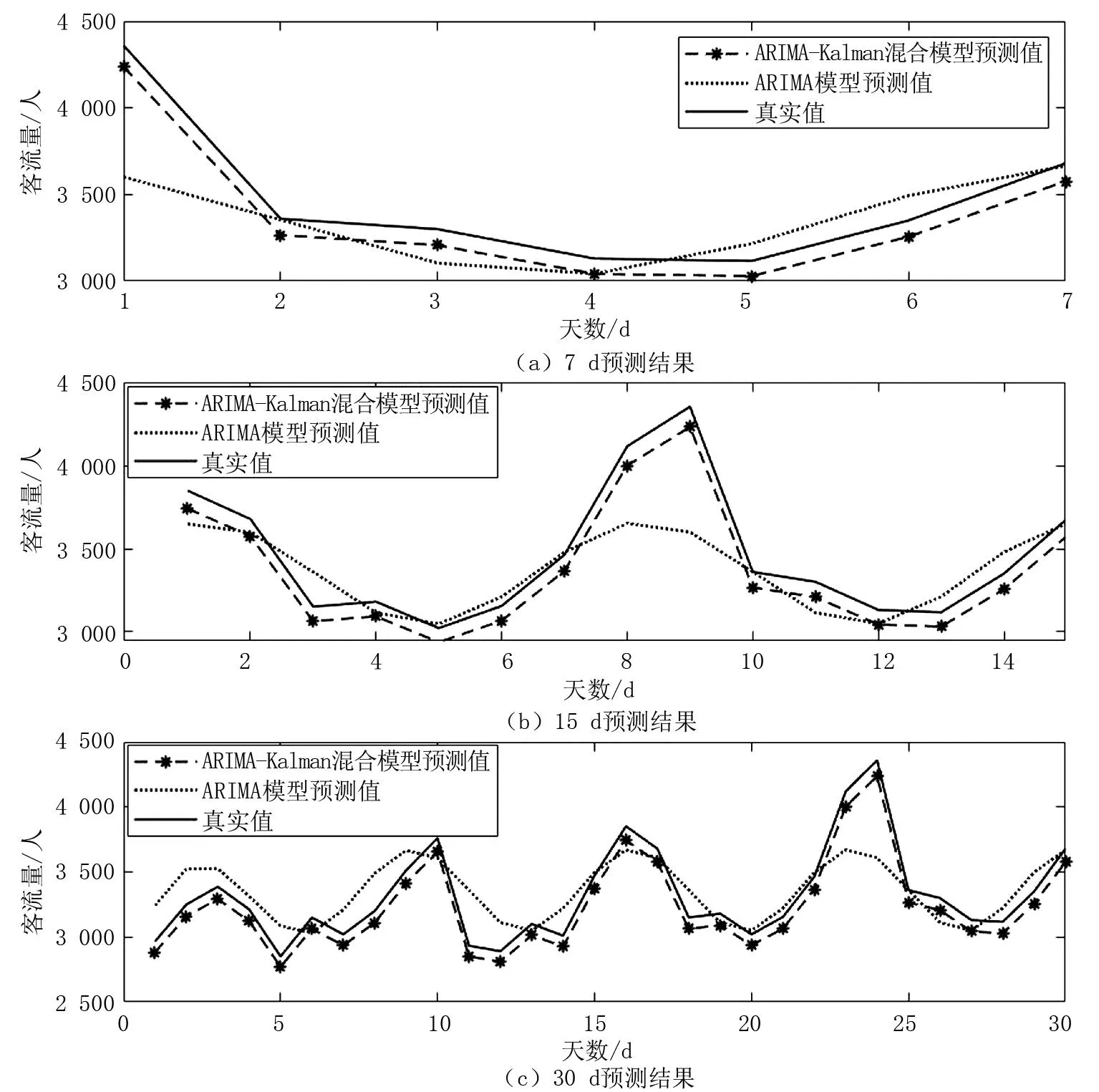
图7 预测结果对比
再分别对比两种模型分别预测未来7 d、15 d和30 d客流量的误差值,如表3所示。表3展示的评判标准对两种方法的比较,均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)能很好地反映出预测值的精确度。由表3可以看出,ARIMA-Kalman滤波混合模型在三种情况下的三种误差值都比单一ARIMA模型的误差值要小。由此证明混合模型能在一定程度上提高预测的精确度,且预测性能比单一ARIMA模型高。
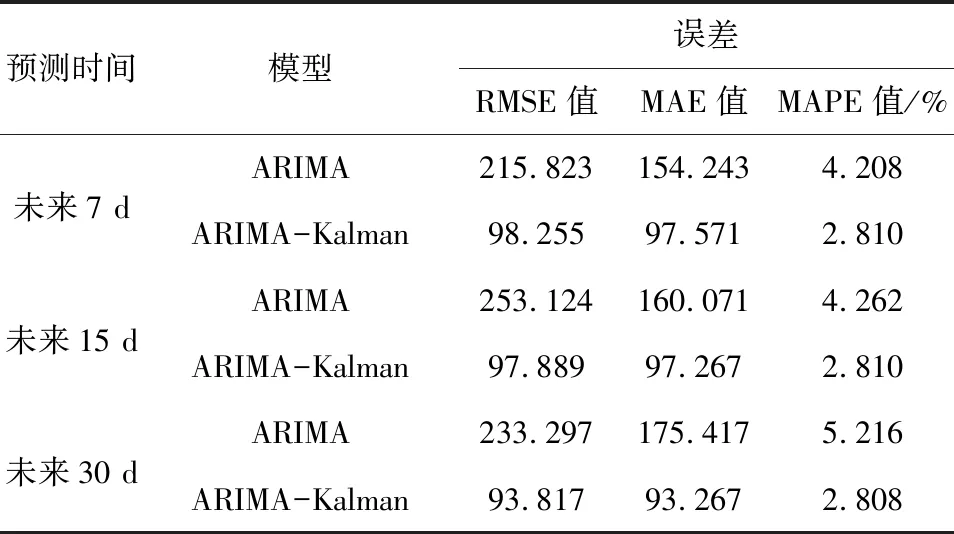
表3 两种模型的三种预测情况的误差值
4 结 语
准确的客流预测有效的保证了运营安全,提高了运输效率,但客流预测过程受到多种因素的影响,有时难以得到精确的预测结果。为了提高客流预测效果,在ARIMA模型基础上引入Kalman滤波降噪机理,提出了一种ARIMA-Kalman滤波混合算法。并通过江门东站2019年全年进站客流数据对模型进行验证,实例结果分析表明,相较于单一ARIMA模型,ARIMA-Kalman滤波混合算法具有更好的预测性能,可用于进站客流预测。

