双馈感应电机最大功率追踪控制

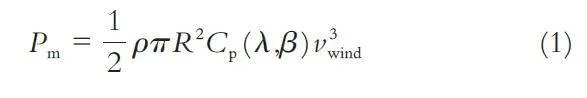
摘 要：为了解决双馈感应电机最大功率追踪困难问题、提高其最大功率追踪效率，提出一种用于双馈感应电机最大功率追踪的多输入多输出二阶滑动模态控制方法. 对双馈感应电机进行建模分析，引入多输入多输出二阶滑膜控制设计过程，简化为含有m 个变量的单输入单输出二阶滑膜控制，进而给出双馈感应电机单输入单输出二阶滑膜控制方法；在阶跃风速、随机风速、低电压穿越三种工况下进行仿真分析，验证了控制方法的有效性和鲁棒性.

关键词：双馈感应电机；最大功率追踪；滑动模态控制；强鲁棒性

中图分类号：TM315

DOI： 10.19504/j.cnki.issn1671-5365.2024.06.08

能源是整个世界发展和经济增长最基本的驱动力，是人类赖以生存和发展的基础. 世界各国能源消费以石油、天然气、煤炭等常规能源为主，2011 年我国能源消费占全球的21.29%，其中常规能源比重达93.31%. 常规能源的大量消耗带来了严重的环境污染，开发利用绿色能源已经成为保护环境、促进可持续发展的有效途径，风能即是一种绿色环保的能源，因此风力发电具有广阔的发展前景.

采用先进的电力电子技术，双馈感应电机（dou⁃bly⁃fed induction generator， DFIG）得到迅速发展. 与带有额定功率换流器的同步感应发电机相比，DFIG具有变速恒频运行、有功功率和无功功率解耦控制、风能向电能的高效率转化等优点. 风速不确定下的最大功率追踪（maximum power point tracking，MPPT）[1]以及电网发生故障时的低电压穿越[2]是其控制设计的主要目标和重要任务. 经典比例-积分（proportional-integral， PI）控制具有结构简单、可靠性高等优点，广泛应用在工业控制领域[3]. PI 控制参数的确定一般来自对被控系统某一运行点的线性化. 然而，风力发电系统具有很强的非线性、不确定性，故双馈感应风力发电机采用PI 控制不能达到理想的效果. 一些启发式算法被提出以进行PI 控制参数的优化：文献[4]提出了群灰狼优化器（groupedgrey wolf optimizer， GGWO）对不同运行场景下的双馈感应电机PI 控制参数进行综合优化，从而实现最大功率追踪；基于知识迁移的细菌觅食强化学习优化（transfer bacteria foraging optimization， TBFO）算法已成功应用到电力系统风险调度中[5]；文献[6]采用综合自适应控制方法以提高电力系统频率稳定性；文献[7]设计了一款基于扰动观测器的滑模控制来实现MPPT，将扰动观测器和滑模控制相结合，从而大幅提高双馈感应电机的鲁棒性；文献[8]提出一种基于扰动观察器的同步发电机变桨距鲁棒控制设计，用来提高风力发电机最大功率追踪能力.

非线性控制、鲁棒控制等先进控制理论的迅速发展，为双馈感应电机的控制提供了一种新的解决思路. 文献[9]设计了一款基于连续时间模型预测控制（continuous-time model predictive control）的双馈感应电机直接功率控制器；文献[10]提出了基于非线性自抗扰控制（nonlinear adaptive disturbance rejec⁃tion control）的双馈感应电机电流控制器，用来提高DFIG 最大功率追踪性能.

本文提出一种二阶滑动模态控制（second ordersliding modes control， SOSMC），利用二阶滑动模态控制结构简单、可靠性高、鲁棒性强等优点，基于Matlab/Simulink 搭建双馈感应电机的系统模型，在随机风速、阶跃风速、低电压穿越三种工况下进行仿真分析，并与PI 控制进行对比，验证控制策略的有效性和鲁棒性.

1 双馈感应电机建模

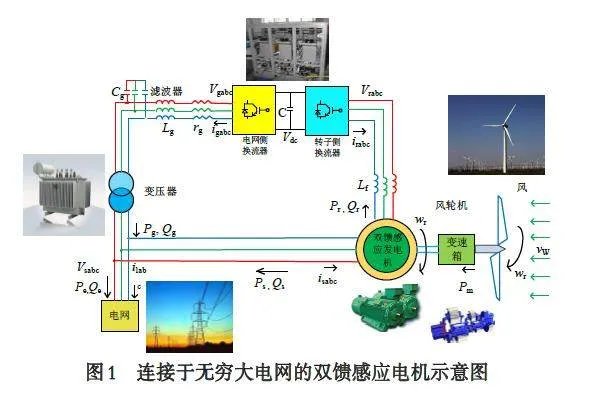
DFIG 的系统结构如图1 所示. 其中，风轮机通过机械轴系统与发电机相连接，同时定子与无穷大电网直接相连，而转子与背靠背换流器相连. 在此，转子侧换流器（rotor-side converter， RSC）旨在对转子角速度和无功功率进行控制，而电网侧换流器（grid-side converter， GSC）的目标则是在无功功率幅值和方向改变的情况下维持直流电压恒定. 由于本文目的在于实现最大功率追踪，因此，仅考虑转子侧换流器的控制设计而忽略电网侧换流器的动态[4].

风轮机所能捕获的机械功率如下所示：

式中ρ 表示空气密度，R 表示风轮机半径，v wind 表示风速. Cp （λ，β ） 为与叶尖速比（tip-speed ratio） λ 和桨距角（blade pitch angle） β 相关的功率因数（power coeffi⁃cient）. β = 0 时功率系数Cp 与λ 关系如图2 所示.

如果风速低于额定值，风轮机将工作于变速模式（variable-speed mode），从而维持Cp （λ，β ） 在C maxp点. 在该工作模式下，风机桨距角控制处于禁用状态，即桨距角β 保持恒定，因此不考虑桨距角控制，即β ≡ 0. 叶尖速比定义如下：

式中各系数ci 分别为： c1 = 0.5176， c2 = 116， c3 =0.4， c4 = 5， c5 = 21， c6 = 0.0068[4].

双馈感应电机完整的动态描述通常由五个非线性微分方程（称Park 模式）得到，其中四个方程描述了在d - q 坐标系下定子和转子的电动力学间的关系，另一个方程描述了机械动力学间的关系.

忽略定子电阻，简化的DFIG 三阶动态方程表示如下[11]：

5 算例分析

5.1 随机风速

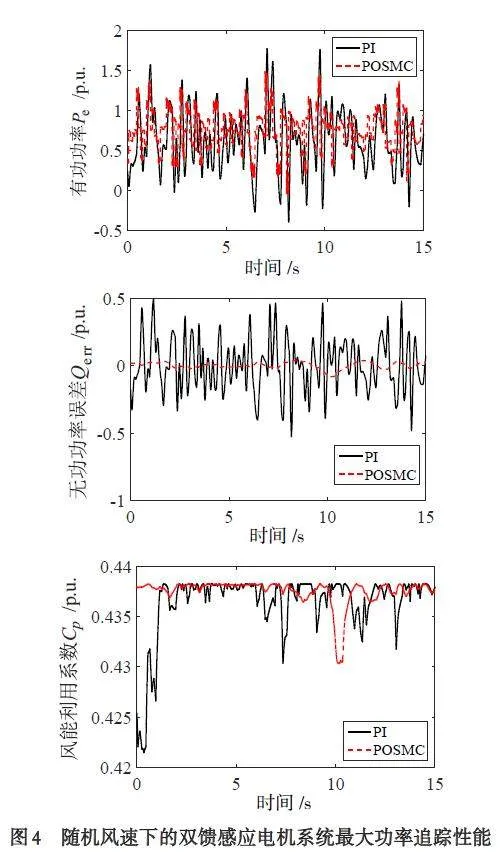
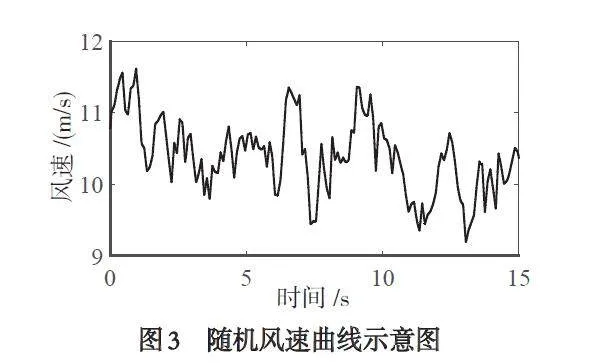
图3 模拟了一个持续时间为15 s、风速变化范围在9 ～ 12 m/s 之间的随机风速，系统响应如图4 所示. 由图4 可见SOSMC 控制比传统的PI 控制具有更小的转子角速度误差和无功功率误差. 另外，采用SOSMC 控制，其功率因数相较于PI 控制更接近于最优值，有功功率波动更小，风能利用系数更加平稳，能在随机风速下捕获更多风能.

5.2 阶跃风速

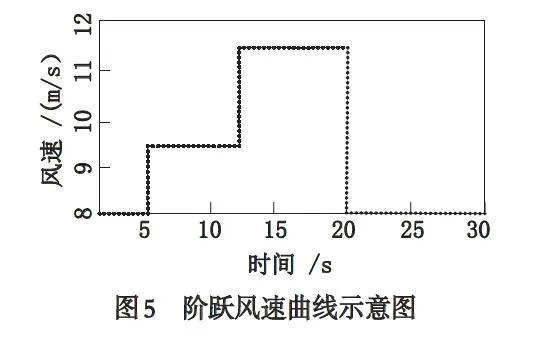
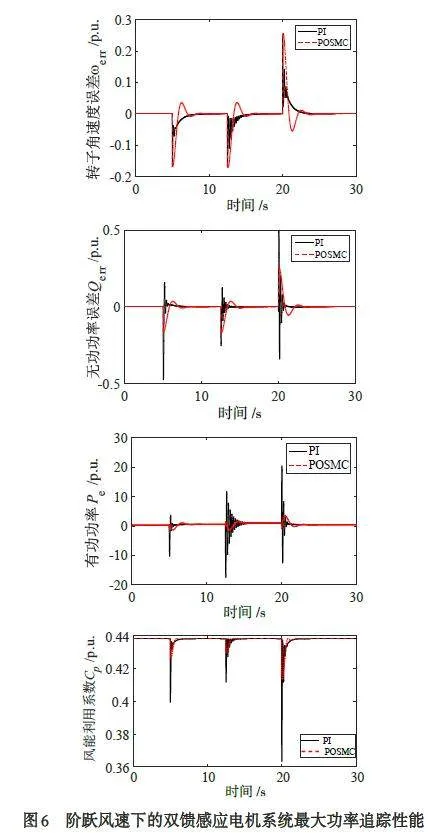
采用阶跃变化信号模拟风速的阶跃变化，对SOSMC 进行仿真测试. 阶跃风速信号如图5 所示，起始风速为8 m/s，在t = 5 s 时刻风速突变为9.5m/s，随后在t = 13 s 时刻风速突变为11.5 m/s，并在t = 20 s 时刻变为初始值8 m/s. 图6 给出了双馈感应电机在SOSMC 控制和PI 控制下的最大功率追踪性能对比，由图6 可见，与PI 控制相比，SOSMC 控制能够更快速地获取最大风能并快速调节有功功率和无功功率，且能够以更短的时间追踪到风能利用系数稳定值.

5.3 低电压穿越

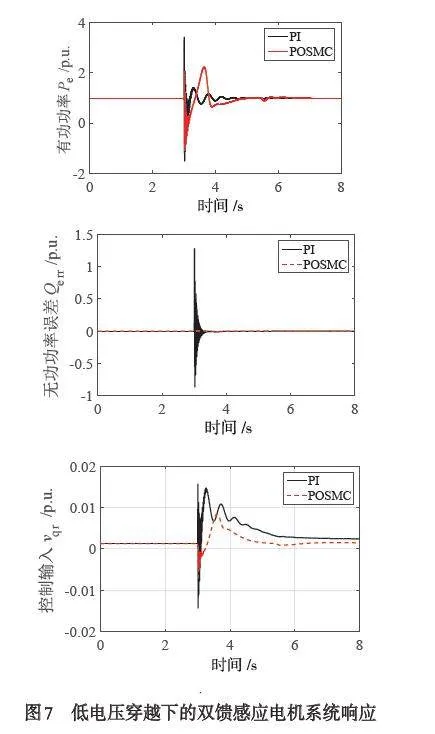
当电网发生故障，或发生大扰动而引起风电场并网点的电压跌落时，在电压跌落的范围内，通常要求风电机组能够不间断地并网运行，称之为低电压穿越. 为测试SOSMC 的低电压穿越能力，模拟一个持续时间为625 ms 的电压跌落. 当t = 3 s 时，电压从从额定值跌落至0.45 p.u.，持续时间为625 ms，随后恢复到0.9 p.u.. 双馈感应电机系统响应如图7 所示，可见电网发生故障时，双馈感应电机采用SOSMC 控制时，其有功功率可以更快速恢复，无功功率误差更小. 可快速恢复双馈感应电机的功率波动，且仅需要更小的控制成本.

6 总结

本文提出了一种二阶滑动模态控制方法，用以实现双馈感应电机最大功率追踪，可总结如下结论：

（1）SOSMC 不依赖于双馈感应电机的精确模型. （2）随机风速、阶跃风速、低电压穿越三种工况下仿真结果表明SOSMC 能够在不同工况下平滑、快速地获取最大风能. （3）在低电压穿越时，SOSMC能够快速调节受扰动的双馈感应电机系统，同时，SOSMC 具有更小的控制成本.

下一步的工作是在实时数字仿真系统RTDS 上搭建双馈风机模型，并应用SOSMC 方法进行仿真，以验证其有效性.

参考文献：

[1] 李鹏， 信鹏飞， 窦鹏冲， 等. 计及光伏发电最大功率追踪的光储微电网功率协调控制方法[J]. 电力系统自动化， 2014，38（4）： 8-13.

[2] 刘淳， 张兴， 周宏林， 等. 含无刷 DFIG 的风电系统低电压穿越极限控制能力分析[J]. 电力系统自动化， 2016， 40（17）：122-128.

[3] LI S H， HASKEW T A， WILLIAMS K A， et al. Control ofDFIG Wind turbine with direct-current vector control con⁃figuration[J]. IEEE Transactions on Sustainable Energy， 2012，3（1）： 1-11. doi：10.1109/TSTE.2011.2167001.

[4] YANG B， ZHANG X S， YU T， et al. Grouped grey wolf op⁃timizer for maximum power point tracking of doubly-fed in⁃duction generator based wind turbine[J]. Energy Conversionand Management， 2017， 133： 427-443. doi：10.1016/j.encon⁃man.2016.10.062.

[5] 韩传家， 张孝顺， 余涛， 等. 风险调度中引入知识迁移的细菌觅食强化学习优化算法[J]. 电力系统自动化， 2017， 41（8）： 69-77.

[6] 金皓纯， 葛敏辉， 徐波. 基于极限学习机的双馈感应风力发电机综合自适应调频参数优化方法[J]. 上海交通大学学报，2021， 55（2）：42-50.

[7] 张维奇， 李富盛， 余涛. 双馈感应电机最大功率跟踪鲁棒滑模控制设计[J]. 电力系统保护与控制， 2020， 48（4）： 47-56.

[8] HU Y L， XIE Y， LI B. Robust variable-pitch control designof PMSG via perturbation observer[J]， Energy Engineering，2021， 118（4）： 911-929. doi：10.32604/EE.2021.014759.

[9] ERROUISSI R， Al-Durra A， MUYEEN S M， et al. Offsetfreedirect power control of DFIG under continuous-timemodel predictive control[J]. IEEE Transactions on PowerElectronics， 2017， 32（3）： 2265-2277. doi： 10.1109/tpel.2016.2557964.

[10] GAO S H， MAO C X， WANG D， et al. Dynamic perfor⁃mance improvement of DFIG-based WT using NADRCcurrent regulators[J]. International Journal of Electrical Powerand Energy Systems， 2016（82）： 363-372. doi： 10.1016/j. ij⁃epes.2016.03.026.

[11] VALENCIAGA F， EVANGELISTA C A. 2-Sliding activeand reactive power control of a wind energy conversion sys⁃tem[J]. IET Control Theory amp; Applications， 2010， 4（11）：2479-2409. doi：10.1049/iet-cta.2009.0437.

[12] PERRUQUETTI W， BARBOT J-P. Sliding Mode Controlin Engineering[M]. Boca Raton： CRC Press， 2002： 53-101.doi：10.1201/9780203910856.

【编校：王露】

基金项目：宜宾学院培育项目（2021PY58）；四川省大学生创新创业训练计划项目（S202310641195，S202310641116）