结合密度峰值和集成过滤器的自训练算法

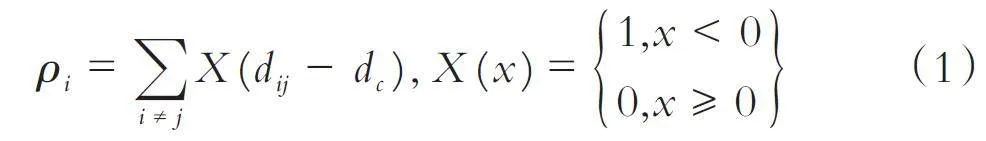
摘 要：准确选取高置信度样本是提升自训练算法分类性能的关键. 针对自训练迭代过程中的误分类样本，提出一种结合密度峰值和集成过滤器的自训练算法：利用密度峰值聚类计算样本的密度和峰值，构建初始高置信度样本集；为了过滤自训练迭代过程中的误分类样本，设计一个集成过滤器，从初始高置信度样本集进一步选择高置信度样本，将其添加进有标签样本集中迭代训练. 在9 个数据集上与4 个相关的自训练算法进行对比实验，结果表明，算法的平均准确率和F 分数分别为67.90% 和65.54%，其分类性能显著优于对比算法.

关键词：自训练；无标签样本；高置信度样本；密度峰值；集成过滤器

中图分类号：TP181

DOI： 10.19504/j.cnki.issn1671-5365.2024.06.03

自训练算法[1]是一种经典的半监督学习算法.半监督学习（Semi-supervised learning， SSL）[2]能够充分利用大量无标签数据和少量有标签数据完成分类任务. 相比较于传统有监督分类利用获取困难、成本高昂的有标签数据进行分类，SSL 降低了数据标签要求，能够以较少的标签成本获得较高的学习性能[3]. SSL 算法主要包括生成式模型[4]、协同训练[5]、基于图的方法[6]和自训练算法等. 其中，自训练算法因其简单、高效且无需考虑数据集的初始假设得到了广泛的讨论和应用[7].

自训练算法在迭代过程中，利用少量有标签样本训练一个基分类器，再利用基分类器从无标签样本中选取出高置信度样本及其预测标签，将选取的样本和标签加入有标签样本集中进行再训练，不断优化直到将所有无标签样本打上标签[8]，其中高置信度样本表示自训练迭代过程中选择的更高概率加入有标签集的样本. 如果样本在迭代过程中被预测为错误标签加进了有标签样本集，即误选取高置信度样本，此错误将会在训练过程中不断加深，因此选取高置信度样本的准确度是影响自训练算法性能的关键因素.

为提升自训练算法分类性能，研究者们提出了不同的高置信度样本的选取方法[9]. Li[10]和Wang[11]等提出了编辑自训练算法（Self⁃training with editing，SETRED）和使用割边的最近邻自训练算法（Self⁃training nearest rule using cut edges， SNNRCE），两个算法使用割边权重统计方法（Cut edge weight statis⁃tic， CEWS）[12]来选取高置信度点，但当割边权重不平衡时，训练效果不佳. Gan 等[13]提出了半监督模糊C 均值聚类的自训练算法（Self⁃training with semi⁃su⁃pervised fuzzy C⁃means， STSFCM），在自训练迭代过程中使用模糊C 均值聚类发现局部数据空间结构，将类簇隶属度大于设定阈值的样本作为高置信度样本，但是当样本类别数较多时阈值的设定较为困难，同时由于未考虑到数据的全局结构信息，难以处理非球形数据样本. 为此，Wu 等[14]提出了一种基于密度峰值的自训练算法（Self⁃training method based ondensity peaks， STDP）.密度峰值聚类（Density peaksclustering， DPC）[15]使用密度峰值构建二维空间中数据间层次关系，能更好地表达样本的整体空间结构，并对任意形状的数据样本有良好的适应性，是一种简单、快速、有效的聚类算法. STDP 算法使用DPC算法发现数据的全局空间结构，解决了非球形分布的数据分类问题.

虽然STDP 算法能够快速有效地发现高置信度无标签样本，且迭代优化速度非常快，但在迭代过程中容易产生错误标记的样本. 一些研究者通过使用局部噪声过滤技术过滤误分类样本来改进自训练算法，如多标签编辑自训练算法、编辑最近邻居和切割边最近邻自训练算法[16]等，在一定程度上解决了错误标记的问题，但是这些过滤技术大多是基于单一分类器进行过滤，过滤效果不够稳定. 为了进一步解决自训练迭代过程中的误分类问题，本文提出一种基于密度峰值和集成过滤器的自训练算法（Self⁃training algorithms based on density peaks and inte⁃grated filters， STDPIF）.STDPIF 构造了一个新颖的集成过滤器，由K 近邻[17]（K⁃nearest neighbor，KNN）、支持向量机[18]（Support vector machine，SVM）、决策树[19]（Classification and regression tree，CRAT）三个分类器组成. 当三个分类器的标签预测结果不一致时，集成过滤器会过滤掉该无标签样本，其预测能力相对于单个过滤器更加稳定. 算法利用DPC 算法发现样本空间结构，将有标签样本的前置和后置无标签样本结点定义为初始高置信度样本，集成过滤器对初始高置信度样本进行过滤，判断样本是否被正确标记，将正确标记的样本组合成为最终的高置信度样本集，从而提高高置信度样本的选取准确度，减少迭代过程中的误分类问题.

1 相关算法

1.1 自训练算法

自训练算法是一种高效而简单的半监督学习方法，能够有效地利用无标签样本对数据进行分类.算法可以采用不同的基分类器和多种选取高置信度样本的方法对模型进行分类. 自训练算法的分类性能主要依赖于高置信度样本选取准确度以及基分类器性能.

定义L 和U 分别为数据集中所有有标签样本集合和无标签样本集合，算法一般流程如下：

Step1： 将L 作为训练集训练得到分类器，使用分类器对U 进行预测；

Step2： 从U 中选取一部分置信度高的样本，用分类器给它们打上伪标签；

Step3： 将赋予伪标签的数据加入训练集，同时将它们从U 中删除，用新的训练集继续训练分类器；

Step4： 返回Step1，直到U 中没有样本时停止.

由于L 会随着高置信度样本的加入而不断扩充，如果在迭代过程中出现样本标签误分类，并将其加入训练集，可能会导致L 中的噪声不断累积，最终使得算法的分类性能下降. 因此更加准确的选取高置信度样本是提升自训练算法分类性能的关键.

1.2 DPC 算法

DPC 算法是由Rodriguez 等人提出的一种基于局部密度和峰值确定类簇中心的聚类算法，它假设每一个类簇中心被密度低于它的样本点包围并与密度较高的样本点之间的距离相对较远[20]，通过计算每一个样本的局部密度和相对距离确定出样本的类簇中心.

DPC 算法中有截断核和高斯核两种计算样本局部密度的方法，本文使用截断核方法，样本xi 局部密度定义为：

其中，d ij 为样本xi 到xj 的欧氏距离，dc 为样本xi 的邻域截断距离，局部密度ρi 即为分布在样本xi 的邻域截断距离范围内的样本个数.

相对距离是指样本xi 与周围最近的密度更大的样本之间的最小距离，样本xi 的相对距离定义为：

δi = minj：ρj gt; ρidij （2）

而对于最高局部密度的样本，其相对距离为：

δi = maxi ≠ jδj， ∀j， ρi gt; ρj （3）

通过计算出它们的类簇中心权值来确定类簇中心，中心权值的定义为：

γi = ρi ⋅ δi （4）

γi 的值越大，xi 越可能成为类簇中心；γi 值相对较小，则xi 一定不是类簇中心点. 即选取局部密度大，峰值高的样本点为可能的类簇中心. 确定类簇中心后，DPC 算法由计算得到的相对距离将其余样本分配到与它们最接近的中心点，完成类簇划分.

1.3 STDP 算法

STDP 算法在自训练迭代过程中加入密度峰值聚类思想，利用密度和峰值揭示数据空间结构，能够更快速地找到置信度高的无标签样本.

STDP 首先使用DPC 算法计算每一个样本的密度和峰值，找到可能的类簇中心，得到每个样本点与最近的类簇中心之间的距离. 然后在L 上训练分类器，在U 中通过DPC 算法揭示的空间结构选择置信度高的无标签样本，由分类器赋予其标签构成高置信度样本集，添加进L 中，并在U 中删除这些样本，重新训练分类器；再从U 中重新选取置信度高的无标签样本由新训练的分类器赋予其标签构成新的高置信度样本集，继续添加进L 中，并在U 中删除这些样本，重复以上步骤，直到没有无标签样本为止.STDP 算法的优点是迭代速度非常快，能有效地发现高置信度无标签样本，但STDP 算法在构建高置信度样本集时存在错误分类且未被去除，错误标签影响算法的分类性能.

2 本文算法

为选取更加准确的高置信度样本，提高自训练算法分类性能，本文将DPC 算法用于无标签初始高置信度样本集的构建，使用集成过滤器对初始集进行重新分类预测，组成准确率更高的高置信度样本集.

2.1 密度峰值选取初始高置信度样本集

算法利用DPC 算法发现样本空间结构，构建样本标记顺序，找出无标签初始高置信度样本集. 首先使用DPC 算法计算出样本xi 的局部密度ρi 和峰值δi，找到距离样本xi 最近且有更大局部密度的样本xj，将xi 指向xj，把被指向的样本xj 称为前置结点，样本xi 称为被指向样本xj 的后置结点.

定义1 样本xi 的前置结点Pxi 为：

Pxi = xj s.t. j，δj = minj：ρj gt; ρidij （5）

计算出每个样本的前置和后置结点即可构建完成样本的标记顺序，样本中密度最高的样本点，其前置结点为自身. 由得到的标记顺序选取高置信度样本点，定义无标签初始高置信度样本.

定义2 样本xi 的无标签初始高置信度样本为：

Sxi = {x } k|xk = Pxi ∨ xi = Pxk ，i ≠ k （6）

由定义1 和定义2 可知，样本xi 的无标签初始高置信度样本由其自身的前置结点和后置结点组成.找到所有有标签样本的后置无标签结点和前置无标签结点，即可组成样本的无标签初始高置信度样本集.

2.2 集成过滤器

本文设计的集成过滤器由KNN、SVM、CRAT三个分类器组成. 利用有标签数据集训练三个分类器，将得到的集成过滤器用于无标签初始高置信度样本集预测筛选. 为利用集成过滤器分类结果选取准确的高置信度样本点，定义最终高置信度样本集.

定义3 最终高置信度样本集S 为：

S = { Sx - si |KNN （si ） ≠ SVM （si ） ∨ SVM （si ）≠ CRAT（si ） } （8）

其中Sx 为无标签初始高置信度样本集，s i 为Sx 中的样本.

由定义3 可知，训练过的集成过滤器对无标签初始高置信度样本集进行分类并打上标签，去除集成过滤器中KNN、SVM、CRAT 三个分类器分类标签不一致的样本，由此组成带有伪标签的最终高置信度样本集.

2.3 基于密度峰值和集成过滤器的自训练算法（STDPIF）

STDPIF 算法在迭代过程中由定义1 和定义2 选取出无标签初始高置信度样本集，再利用集成过滤器对初始集进行预测，将分类标签一致的高置信度样本重新组成准确率更高的高置信度样本集，将其加入有标签样本集中进行分类预测. 重复进行，直到无标签样本集中没有样本为止. 算法的伪代码如下：

算法1 STDPIF 算法

输入：有标签数据集L ，无标签数据集U

输出：分类器H

初始化高置信度样本集S = ∅

利用公式（1）和（2）求出样本的局部密度ρ 和峰值δ

While U ≠ ∅ DO

for x i ∈ L

根据定义1 确认样本x i的无标签初始高置信度样本S xi

S = S ⋃ S xi

End for

利用L 训练KNN、SVM 和CART

for s i ∈ S

if K N N （s i ） ≠ S V M （s i ） or C A R T （s i ） ≠ S V M （s i ）

S = S -s i

End if

End for

L = L ⋃ S ， U = U -S

End while

使用L 训练KNN

Return H

3 实验结果与分析

本文实验环境为Windows 10 64 位操作系统、Intel Core i7 处理器、16 GB 内存、MATLAB R2019b编程环境.

3.1 实验设置

为验证本文算法的有效性，选取SETRED[12]、STSFCM[15]、STDP[16]、STDPCEW[20]这4 个算法与本文STDPIF 算法进行对比实验. 所有算法的参数根据算法的原文进行设置. 为了与STDP 和STDPCEW 算法保持一致，本文STDPIF 算法的截断距离设置为α = 2. 参数设置如表1 所示.

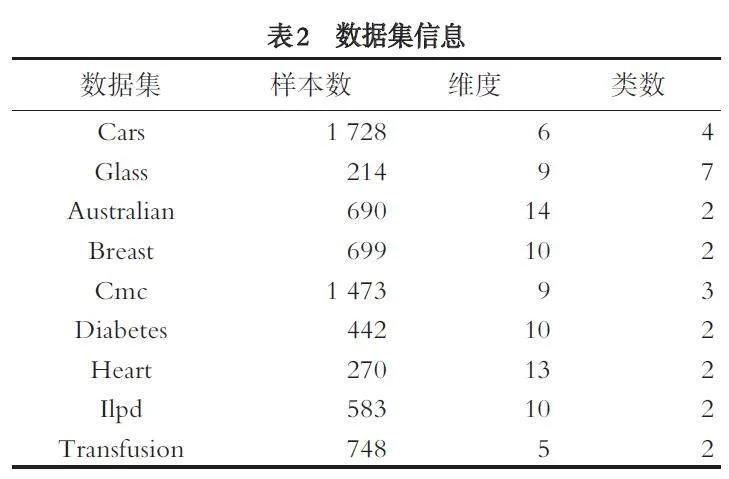
选取Cars、Glass、Australian、Breast、CMC、Diabe⁃tes、Heart、Ilpd、Transfuion 这9 个数据集进行实验，数据集的相关信息如表2 所示，9 个数据集均来源于公开的UCI 数据库.

3.2 实验结果及分析

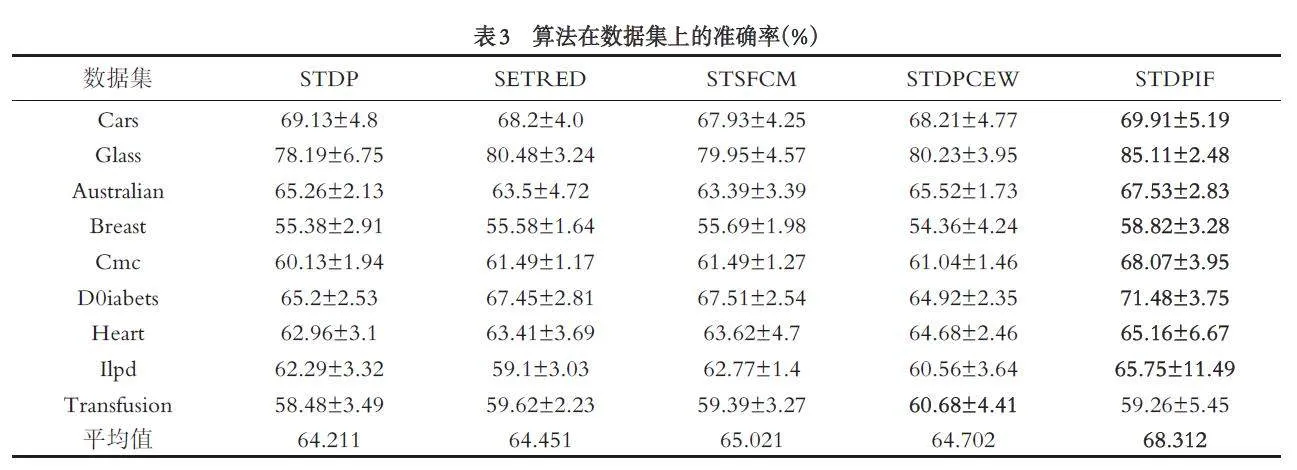
将初始有标签样本比例设为10%，在每一次试验中随机选取，其余的90% 作为无标签样本，将准确率（Accuracy）和 F 分数（F-score）作为算法分类性能的评价标准. 5 个算法按照表1 设定参数分别在9 个数据集上运行50 次，计算每个算法50 次实验结果后的两种评价指标的平均值与标准差，实验结果如表3 和表4 所示，为直观显示，对5 个算法在每个数据集上的最佳性能加粗显示.

表3 的结果表明，对所选取的9 个数据集，本文算法在8 个数据集上的准确率要优于4 个对比算法，仅在Transfusion 数据集上，本文算法的准确率低于SETRED、STSFCM、STDPCEW 这三个对比算法，但要高于STDP 算法. 在Cmc 数据集上，STDPIF 算法的准确率与第二名STSFCM 算法的差距最大，高出了6.58 个百分点；在Heart 数据集上，STDPIF 算法的准确率与第二名STDPCEW 算法的差距最小，仅高出0.48 个百分点.

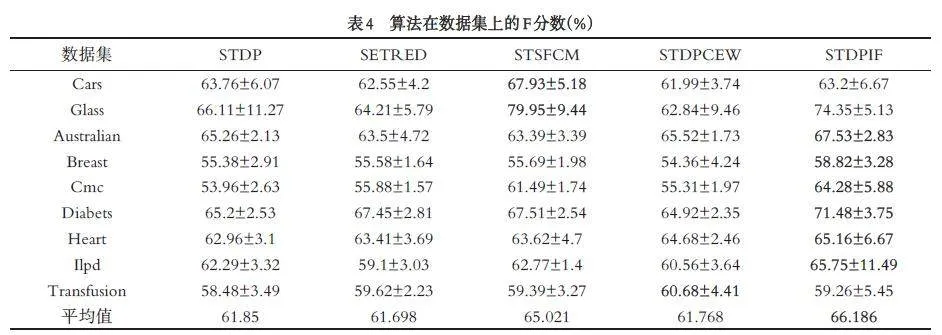
表4 的结果表明，在多数数据集上本文算法的F分数也取得最高. 在Cars 数据集上，STDPIF 算法的F 分数低于STSFCM、STDP 算法，但要高于SETRED 和STDPCEW 算法；在Glass 数据集上，STDPIF 算法的F 分数低于STSFCM 算法，但高于其他3 个对比算法. 在其他6 个数据集上，STDPIF 算法的F 分数均为最高. 从表4 和表5 可知， 4 个对比算法在不同数据集上的性能差异很大，仅在个别数据集上的准确率和F 分数超过本文算法，本文算法在多数数据集上的分类性能均取得最优. 实验结果表明，本文算法利用DPC 和集成过滤器能够有效地提升选取高置信度样本的准确率，降低误分类风险，提高自训练算法的分类性能.

3.3 有标签样本比例对算法性能的影响

自训练算法的高效在于可以利用少量有标签样本进行训练，但有标签的比例过低会导致获取到的信息太少，难以进行训练；而过多的有标签数据不一定会增加有用信息，还会影响其高效性能. 因此，本文设置了不同比例的有标签样本进行实验，分析其对算法分类性能的影响.

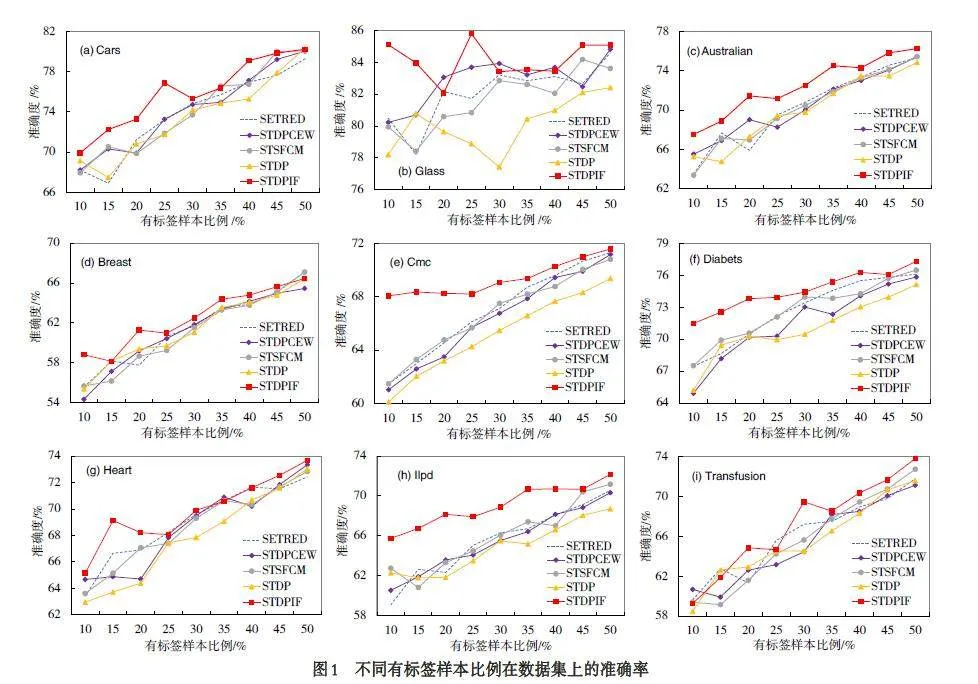
将初始有标签样本比例最低设置为10%，最高设置为50%，每次实验比例增加5%. 记录5 个算法在每个数据集上运行50 次的准确率平均值，实验结果如图1 所示.

结果表明，随着有标签样本比例的增加，5 个算法的准确率也会逐渐增加，在Glass 数据集上5 个算法的性能表现波动比较大，这是因为Glass 数据集的类别数较多，每个类的初始有标记样本较少，5 个算法在每次实验中都无法有效地训练出良好的分类器，导致了实验结果的不稳定. 由图1 整体可知，当有标签样本的比例较低时，本文算法的性能优于其他对比算法，这表明本文算法能够在有标签样本较少的情况下，利用集成过滤器更好的选取无标签高置信度样本进行训练.

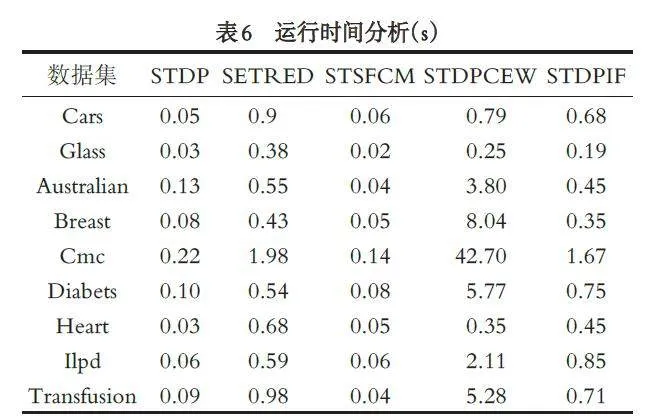
3.4 实验运行时间分析

表6 为5 个算法在9 个数据集上的平均运行时间，各算法按表3 设定的参数以10% 的初始有标签样本比例运行10 次. 由表6 可知， STSFCM 和STDP的耗时远低于另外3 个算法，这是因为两个算法的复杂度都为O （n2 ），SETRED、STDPDCEW 的耗时高是因为其复杂度都为O （n3 ）. STDPIF 在7 个数据集上的耗时只高于STDP 和STSFCM，因为STDPIF与STDP 的复杂度相同. 由上述分析可知，STDPIF能够以较短的训练时间得到更高的分类性能.

4 结语

针对自训练迭代过程中选取的高置信度样本可能被误分类的问题，提出一种基于密度峰值和集成过滤器的自训练算法（STDPIF）.算法首先利用密度峰值计算得到初始高置信度样本集，再构建集成过滤器对初始集进行过滤得到最终高置信度样本集，降低了样本被误分类的风险. 在9 个数据集上和4个对比算法进行了大量的实验并选取准确率和F 分数作为评价指标，结果表明STDPIF 算法的平均准确率和F 分数高于4 个对比算法. 同时对有标签样本比例对算法的性能影响进行了实验分析，实验结果表明在初始有标签样本比例较低的情况下，本文算法的性能与对比算法相比有较大的提升. 后续的工作将继续研究提高选取高置信度样本准确度的方法，尤其是在有标签样本较少的情况下选取无标签高置信度样本的方法，构建更加准确的高置信度样本集.

参考文献：

[1] LI B， WANG J K， YANG Z G， et al. Fast semi-supervised selftrainingalgorithm based on data editing[J]. Information Sciences，2023（626）： 293-314. doi：10.1016/J.INS.2023.01.029.

[2] Yoon H， Kim H. Label-noise robust deep generative modelfor semi-supervised learning[J]. Technometrics， 2023， 65（1）：83-95. doi：10.1080/00401706.2022.2078413.

[3] 刘学文， 王继奎， 杨正国， 等. 近亲结点图编辑的Self-Training 算法[J]. 计算机工程与应用，2022，58（14）：144-152.

[4] 曹卫东，许志香，王静. 基于深度生成模型的半监督入侵检测算法[J]. 计算机科学，2019，46（3）：197-201.

[5] 龚彦鹭，吕佳. 结合主动学习和密度峰值聚类的协同训练算法[J]. 计算机应用，2019，39（8）：2297-2301.

[6] CHONG Y， DING Y， YAN Q， et al. Graph-based semisupervised learning： A review[J]. Neurocomputing， 2020（408）：216-230. doi：10.1016/j.neucom.2019.12.130.

[7] 吕佳，刘强，李帅军. 结合密度峰值和改进自然邻居的自训练算法[J]. 南京大学学报（自然科学），2022，58（5）：805-815.

[8] 卫丹妮，杨有龙，仇海全. 结合密度峰值和切边权值的自训练算法[J]. 计算机工程与应用，2021，57（2）：70-76.

[9] 刘学文，王继奎，杨正国，等. 密度峰值隶属度优化的半监督Self-Training 算法[J]. 计算机科学与探索，2022，16（9）：2078-2088.

[10] LI M， ZHOU Z H. SETRED： Self-training with editing[C]//Ho T B， Cheung D， Liu H. Advances in KnowledgeDiscovery and Data Mining. Berlin， Heidelberg： Springer，2005： 611-621. doi：10.1007/11430919_71.

[11] WEI Z H， WANG H L， RU Z. Semi-supervised multilabelimage classification based on nearest neighbor editing[J].Neurocomputing， 2013（119）： 462-468. doi： 10.1016/j. neu⁃com.2013.03.011.

[12] 孙彩锋. 基于密度峰值聚类和无参数滤波器的自训练方法[J]. 计算机应用与软件，2022，39（12）：318-327.

[13] GAN H， TONG X， JIANG Q， et al. Discussion of FCM al⁃gorithm with partial supervision[C]//Proceedings of the 8thInternational Symposium on Distributed Computing and Ap⁃plications to Business， Engineering and Science. Beijing： Pub⁃lishing House of Electronics Industry， 2009： 27-31.

[14] WU D， SHANG M， LUO X， et al. Self-training semisupervisedclassification based on density peaks of data[J].Neurocomputing， 2018（275）： 180-191. doi： 10.1016/j. neu⁃com.2017.05.072.

[15] RODRIGUEZ A， LAIO A. Clustering by fast search andfind of density peaks[J]. Science， 2014，344（6191）： 1492-1496.doi：10.1126/science.1242072.

[16] 李帅军，吕佳. 结合合成实例与adaboostENN 密度峰值自训练算法[J]. 重庆师范大学学报（ 自然科学版）， 2022， 39（4）：105-113.

[17] 吴强. 基于局部均值k 近邻和密度峰值的实例约简[J]. 统计与决策，2022，38（24）：10-16.

[18] 李福祥，王雪，张驰，等. 基于边界点的支持向量机分类算法[J]. 陕西理工大学学报（自然科学版），2022，38（3）：30-38.

[19] 张亮，宁芊.CART 决策树的两种改进及应用[J]. 计算机工程与设计，2015，36（5）：1209-1213.

[20] 徐鑫，曹原. 基于加权直觉模糊兰氏距离的密度峰值聚类算法[J]. 陕西师范大学学报（自然科学版），2023，51（1）： 101-110.

【编校：王露】

基金项目：甘肃省自然科学基金项目“深度学习在高原夏菜质量分级中的应用研究”（21JR1RA283）