高机动履带车辆行驶啮合稳定性影响机理及仿真分析

摘 要：本文在重点分析履带车辆推进装置啮合稳定性影响因素的基础上，通过履带车辆多体动力学仿真分析模型对其推进装置的啮合稳定性进行仿真分析，所得结果有助于履带推进装置的优化设计，为进一步提高履带车辆行驶系统的啮合稳定性奠定了基础。

关键词：履带车辆；啮合稳定性；仿真分析

On the Meshing Stability Influence Mechanism

and Simulation Analysis of High Mobility Tracked Vehicles

Wu Juan1 Hao Kui1 Xie Yanchao1 Gao Junfeng Liu Dan2

（1.Vehicle Engineering Department，Baotou Vocational amp; Technical College，Baotou，Inner Mongolia 014035;

2.Scientific Research Institute，Inner Mongolia First Machinery Group Co.，Ltd.，Baotou，Inner Mongolia 014032）

Abstract：Based on the analysis of meshing stability influence factors of tracked vehicles，the meshing stability of the propulsion device of tracked vehicle is simulated and analyzed by the multi-body dynamics simulation analysis model.The results obtained are helpful to the optimal design of the tracked propulsion device and lay a foundation for further improving the meshing stability of the tracked vehicle driving system.

Key words：tracked vehicles;meshing stability;simulation analysis

1 引言

履带推进装置由于其卓越的通过能力和越障能力而被广泛应用在军用、矿业、林业等领域。高速履带车辆的高速化是提升车辆反应能力、执行能力和快速部署能力的关键。近年来，随着发动机和电机性能的快速发展，各国均将提升履带车辆的越野速度及行驶性能作为发展目标。然而，仅有高性能的动力系统并不能很好地实现履带车辆的高速化，因为随着车辆行驶速度的增加，履带推进装置与地面间的相对速度也随之增加，致使地面对履带推进装置的冲击速度增加，同时履带推进装置各零部件间的磨损增加，导致整个推进装置推进效率下降。［1］如美国的M1坦克装甲车辆，在动力1500马力的推动下其理论最高车速可达100km/h，但受传动、振动、牵引和机械效率等因素的影响，最终时速上限为72km/h。［2］因此，研究履带推进装置的啮合稳定性及功率损耗机理，对实现履带车辆的高速化非常重要。

履带车辆行动系统由推进装置和悬挂装置组成，其中推进装置由驱动轮、支重轮、诱导轮、托带轮和履带板等组成，［3］是实现履带车辆高速化的关键装置之一。本文在重点分析履带车辆推进装置啮合稳定性影响因素的基础上，通过履带车辆多体动力学仿真分析模型对其推进装置的啮合稳定性进行仿真分析，根据仿真结果对推进装置的啮合稳定性进行评估，为工程实践提供理论支撑。

2 履带车辆推进装置啮合稳定性影响因素分析

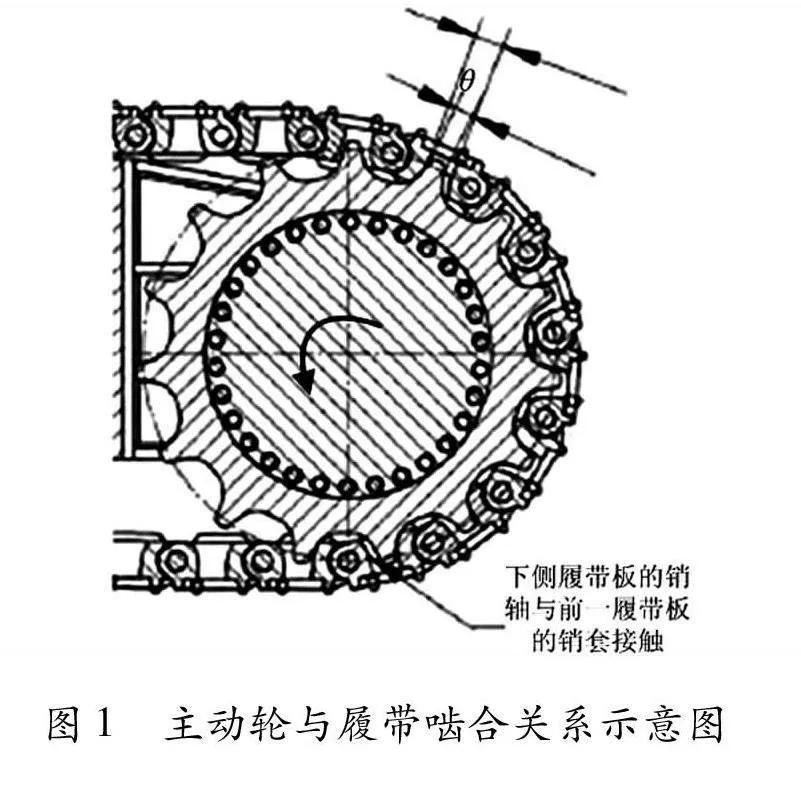
履带车辆推进装置啮合稳定性指履带车辆主动轮轮齿和履带板稳定、平稳啮合进入并啮合退出的性能，对于减小振动噪声，延长主动轮轮齿和履带板的使用寿命，提高设备性能具有非常重要的作用。军用式履带车辆一般采用后置后驱行驶，主动轮和履带啮合关系如图1所示。

从图1可以看出，当履带车辆前进时，动力后置后驱，主动轮是逆时针旋转的，主动轮和履带板之间的啮合过程如下：主动轮下侧履带板的销轴与前一块履带板的销套接触，下侧履带板随主动轮转过某一角度θ并进入啮合，此时主动轮齿面与已经进入主动轮上的销套无相对运动，下侧履带板的销轴与前一块履带板的销套铰接处存在相对运动，将产生摩擦力。因此，主动轮与履带啮合过程中的冲击速度和冲击力将影响到履带车辆的啮合稳定性。

2.1 冲击速度对啮合稳定性的影响

履带板通过销轴和端联器连接成履带环，车辆行驶过程中，主动轮齿通过拨动端联器带动履带环的运动，端联器与主动轮啮入冲击的大小与其法向冲击速度有关，将端联器假设成圆截面，则端联器啮入主动轮产生冲击的情况如图2所示。

从图2可以看出，端联器啮入时前一瞬间在K点速度与整条履带的速度相同，当端联器与主动轮开始接触，则端联器上K点的速度在瞬间变为K点位于主动轮上的线速度，端联器的速度由Vdk变为Vik时，使得端联器与主动轮齿面产生斜冲击，设其冲击速度为Vk。

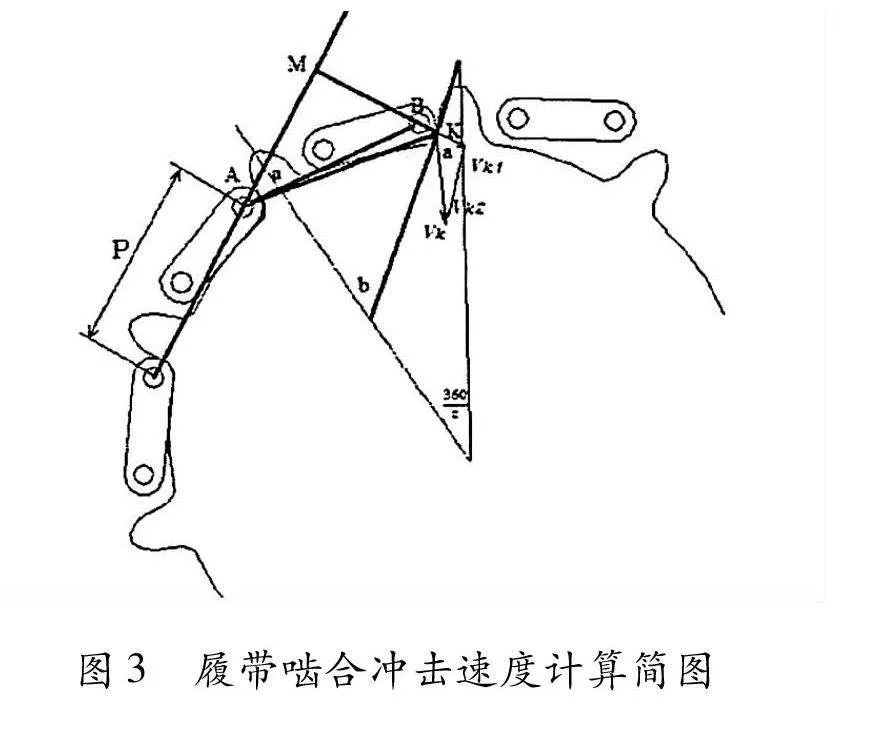
根据物体运动原理，将啮合模型等效为主动轮固定，履带相对于主动轮以角速度ω啮入，则建立端联器和主动轮齿啮合时的冲击速度模型如图3所示。

根据图3得到啮合时的冲击速度为：

Vk=LKA·ωkA=AM[]cosα·ωKA

=Psin360[]z+r[]2[]cosα·ωKA（1）

式中，

P——主动轮节距；

r——齿形角；

α——线段AM与AK之间的夹角；

ωKA——K点相对于A点的角速度。

通过上式可以看出，履带车辆在行驶过程中，履带和主动轮齿之间的啮合稳定性除了与履带张紧力有关，主动轮节距、齿数、齿形角和端联器与主动轮之间的相对速度等都是影响其稳定性的主要因素。

2.2 啮合冲击力对啮合稳定性的影响

根据运动的相对性原理，整个履带板和主动轮的啮合过程在啮入瞬间可以等效为质量为m的端联器以冲击速度Vk在啮合点K以一定的角度与主动轮齿发生冲击，在主动轮扭矩的作用下，将端联器与主动轮的接触可简化为圆柱体与凹型圆柱面在压力下的接触，如图4所示。

由赫兹应力公式可得长方形接触区域的宽度b如公式（2）所示：

（2）

端联器和主动轮的变形深度如式（3）和式（4）所示：

h1=ρ1-ρ21-b2（3）

h2=ρ2-ρ22-b2（4）

则端联器和主动轮齿之间的接触刚度为：

k=p[]h1+h2（5）

式中，

p——端联器和主动轮间单位接触压力；

l——主动轮齿宽；

μ1、μ2——端联器和主动轮材料的泊松比；

ρ1、ρ2——端联器和主动轮在接触点K处的曲率半径；

E1、E2——端联器和主动轮材料的弹性模量。

根据公式（2）～（5），建立端联器与主动轮接触时的动力学模型为：

mx+cx·[]+kx¨[]=0（6）

式中，

c——端联器和主动轮接触阻尼系数；

x、x·[]、x¨[]——端联器与主动轮接触位移、速度和加速度。

初始条件：

x（0）=0，x（0）=Vksinα（7）

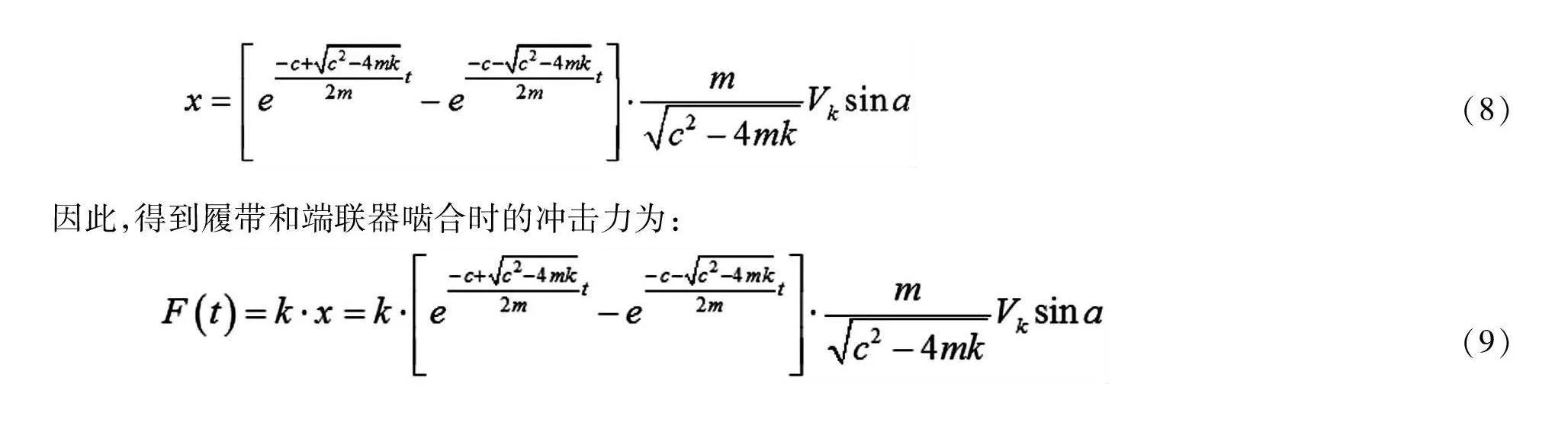
将式（7）带入式（6），积分求解得

（8）

因此，得到履带和端联器啮合时的冲击力为：

（9）

从式（9）可以看出，履带和主动齿轮之间的啮合稳定性除了与冲击速度有关，其履带板端联器和主动轮的材料属性、端联器和主动轮接触部位的曲率半径、端联器质量和主动轮的齿宽也是影响啮合稳定性的重要因素。

3 履带车辆行动系统动力学模型的建立

履带车辆多体动力学模型的建立实际就是通过定义刚体、弹性体、约束、力以及接触等来确定车辆的各组成部件之间的特性与连接关系，进而形成一系列多体动力学控制方程并进行求解的过程。［4］本文以某履带车辆行动系统为研究对象，根据其总体布置、质量、惯量和重心等属性，基于RecurDyn软件建立履带车辆的行动系统动力学仿真模型，在建模过程中将复杂的履带车辆底盘系统简化为车体及各重要组件、履带推进装置、悬挂装置等子系统，其中履带推进装置由履带环、负重轮、主动轮、拖带轮、诱导轮及履带调整器等组成，悬挂装置主要由扭杆弹簧、减振器和弹性限位器等组成，其他模块都以质量块进行代替，多体动力学模型如图5所示。

如图5所示，该动力学模型由车体及重要组件、履带推进装置和行驶路面组成，其中履带推进装置由主动轮前置和诱导轮后置的行驶组成，单侧履带系统包括1个主动轮、1个诱导轮、6个负重轮、3个拖带轮一机履带板。各部件之间通过球较和力元连接在一起，车体和动力及传动装置分别通过多点悬置进行连接，车体和其他组件通过固定副进行连接。车体和主动轮、拖带轮、诱导轮之间采用旋转副进行连接，系统拓扑结构如图6所示。

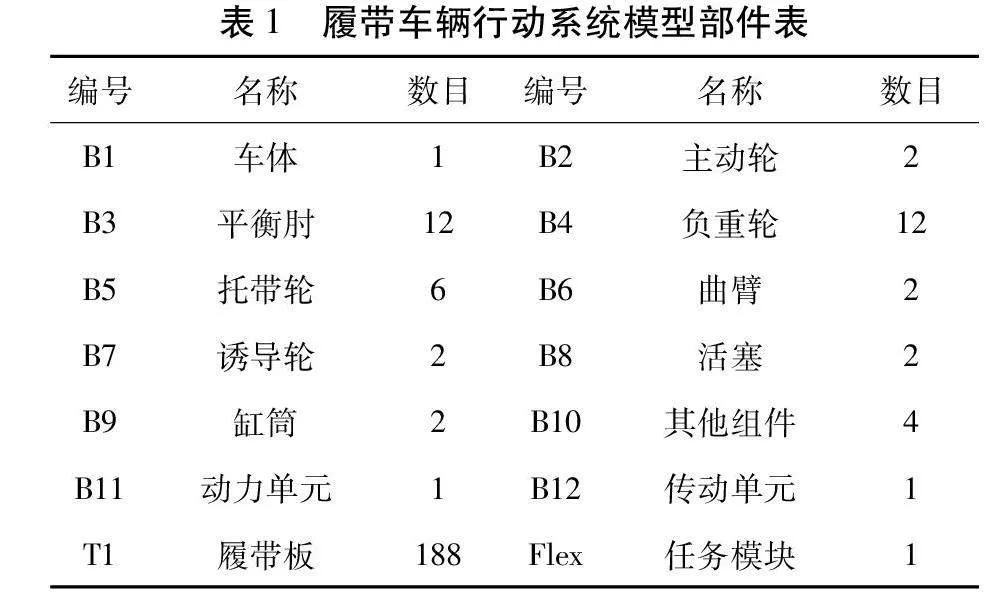
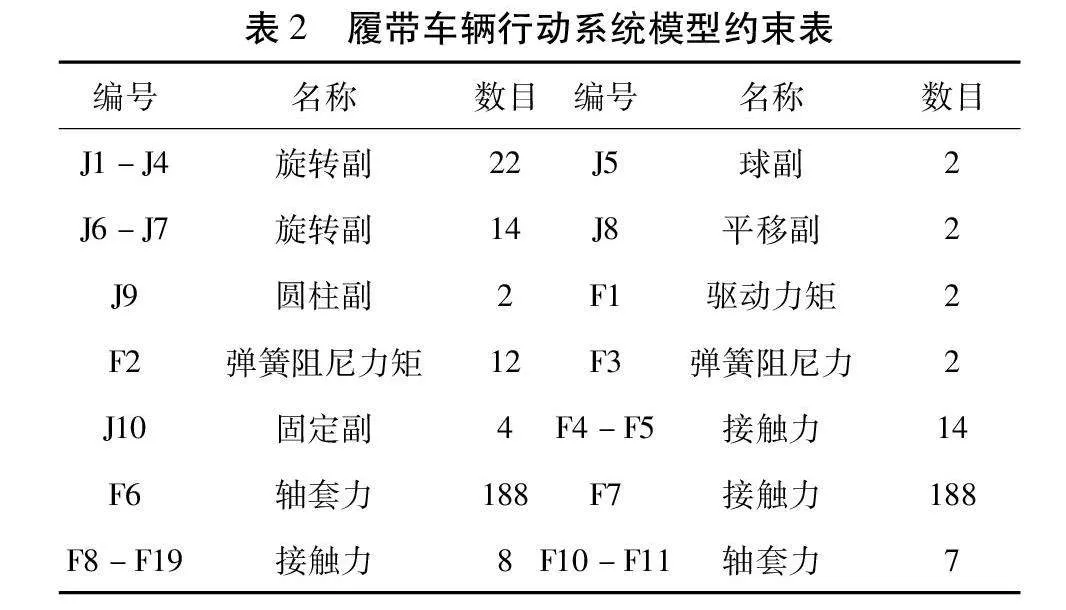
拓扑结构模型部件表如表1所示。

在建模过程中，由于整车采用扭杆弹簧，因此悬挂系统采用转动弹簧阻尼驱动器来模拟，作用扭矩为：［5］

T=T0-KTθ-CTθ·[]（10）

其中，

θ、θ·[]——扭杆弹簧扭转角（deg）和扭转角速度（deg/s）;

T0——静平衡位置，平衡肘预扭矩，N/m；

KT、CT——弹簧刚度和阻尼系数。

根据整车布置及结构尺寸、重心、部件参数等情况，定义履带与主动轮、履带与负重轮及负重轮与地面之间的接触关系，得到重载履带车辆多体动力学模型。

4 履带车辆行驶啮合稳定性仿真分析

根据前面履带啮合稳定性影响因素的分析，本文基于所建立的重载履带车辆行动系统多体动力学模型进行不同预紧力和不同速度情况下的履带车辆直驶工况仿真分析计算，分析履带预紧力和车辆行驶速度对履带行动系统啮合稳定性的影响。

4.1 不同车速对履带行驶啮合稳定性的仿真分析

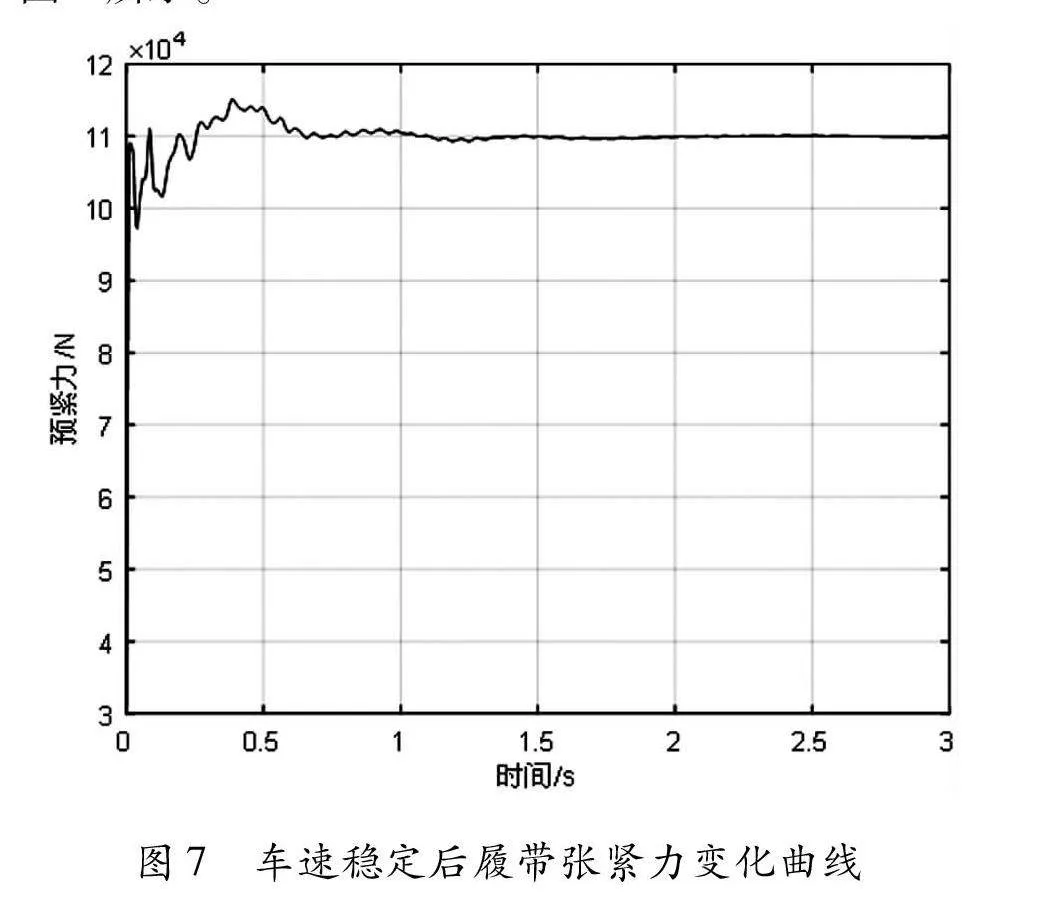
在建立的多体动力学模型中，将履带预紧力设定为固定值110kN，设定车辆行驶速度为20km/h、30km/h、40km/h和50km/h，行驶路面为砂石路面，进行啮合稳定性仿真分析，则不同行驶车速在砂石路面行驶时，车速稳定后履带张紧力的变化曲线如图7所示。

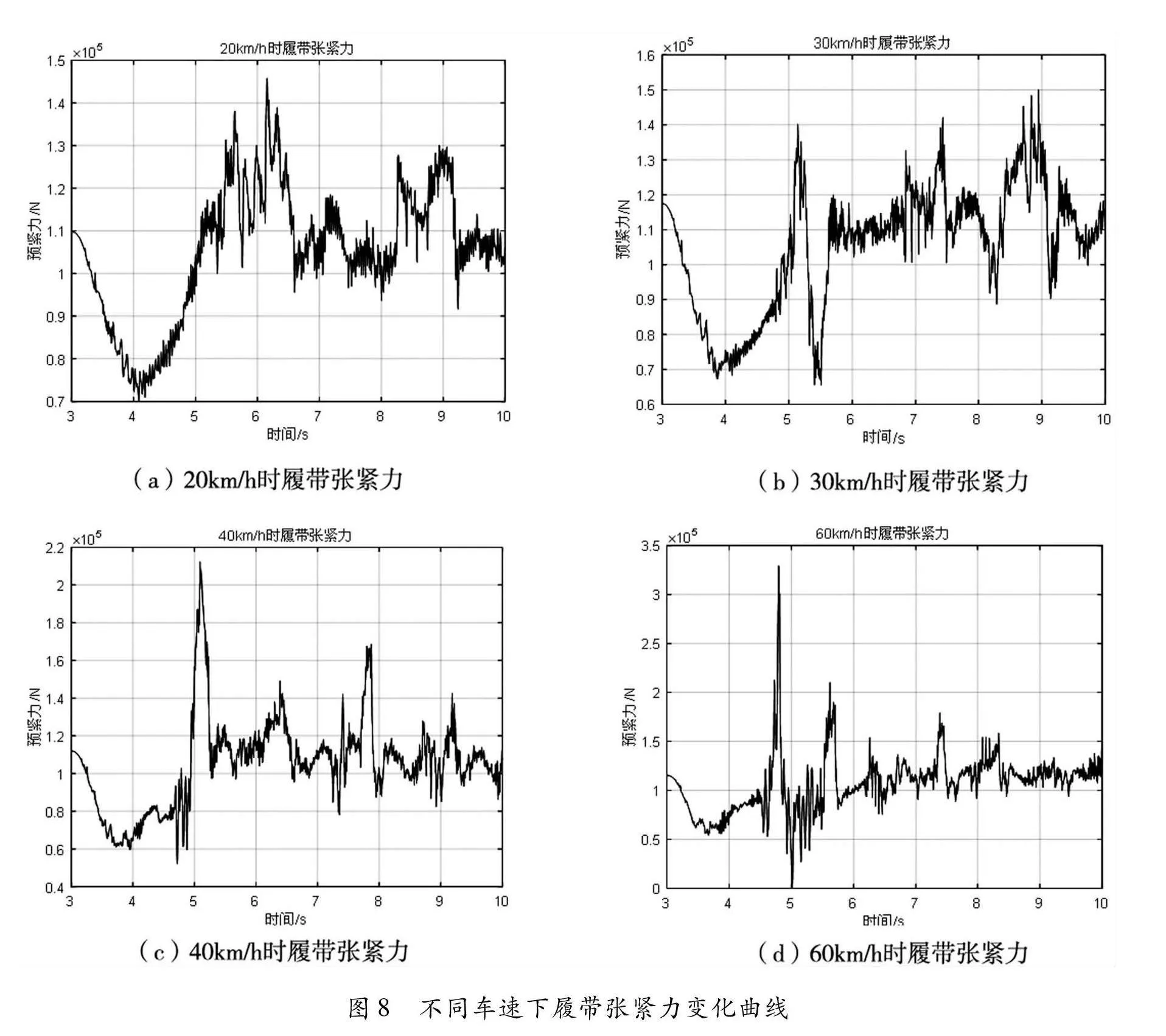
不同车速下履带张紧力的变化情况如图8所示。

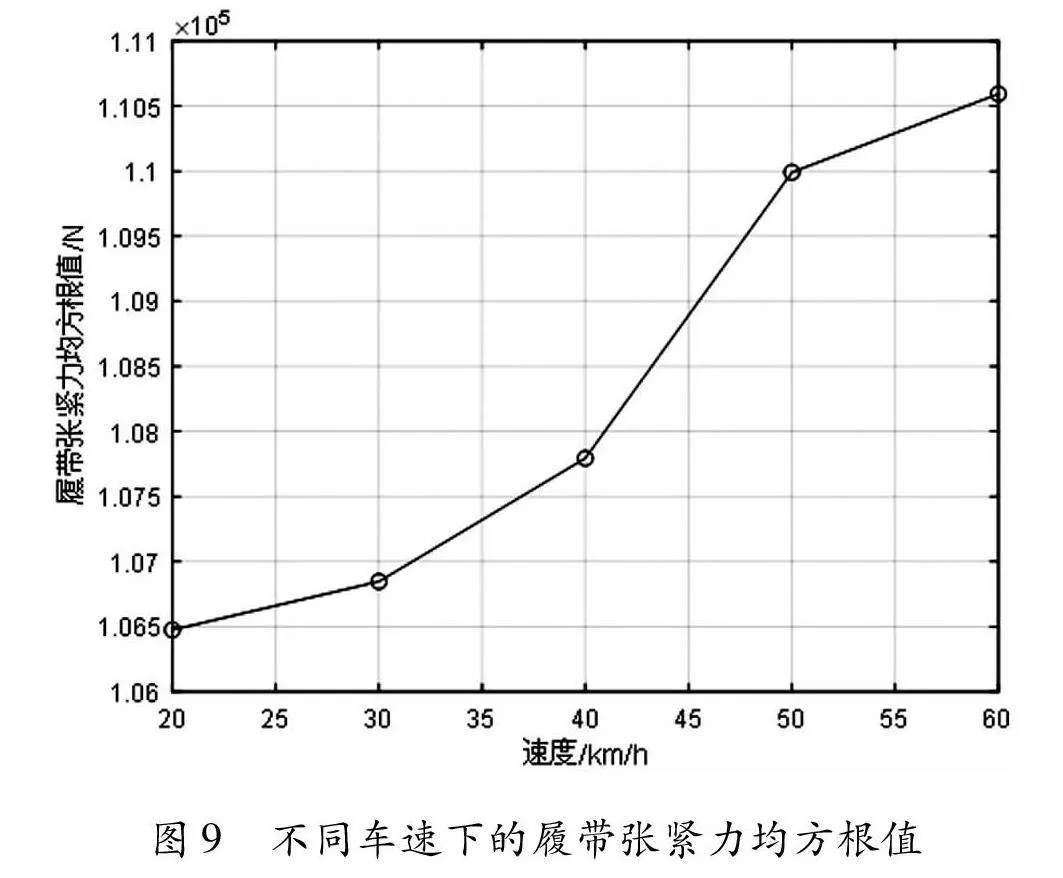
从图8可以看出，履带车辆行驶过程中，不同车速下履带张紧力围绕其预张紧力（110kN）上下波动，并且从幅值上可以看出，履带张紧力随着车速的增大有所增加。以履带张紧力的均方根值作为评价指标，计算不同车速下履带张紧力的均方根值，得到履带张紧力均方根值随车速的变化曲线如图9所示。

从图9可知，在预紧力相同的情况下，随着车速的增大，履带的张紧力也随之增加。

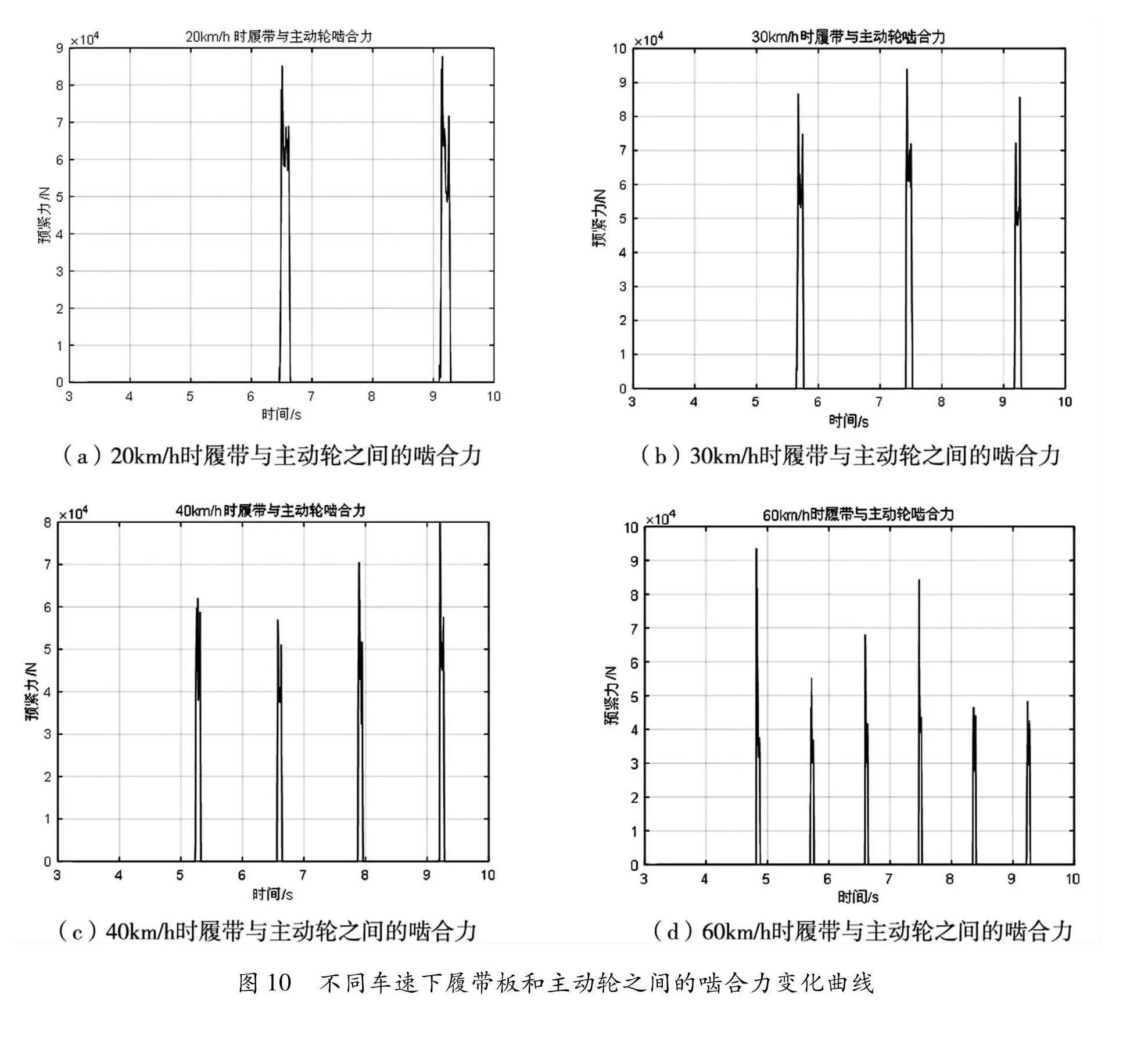
通过不同行驶车速下的履带车辆动力学仿真，测得某履带板与主动轮之间啮合力的变化曲线如图10所示。

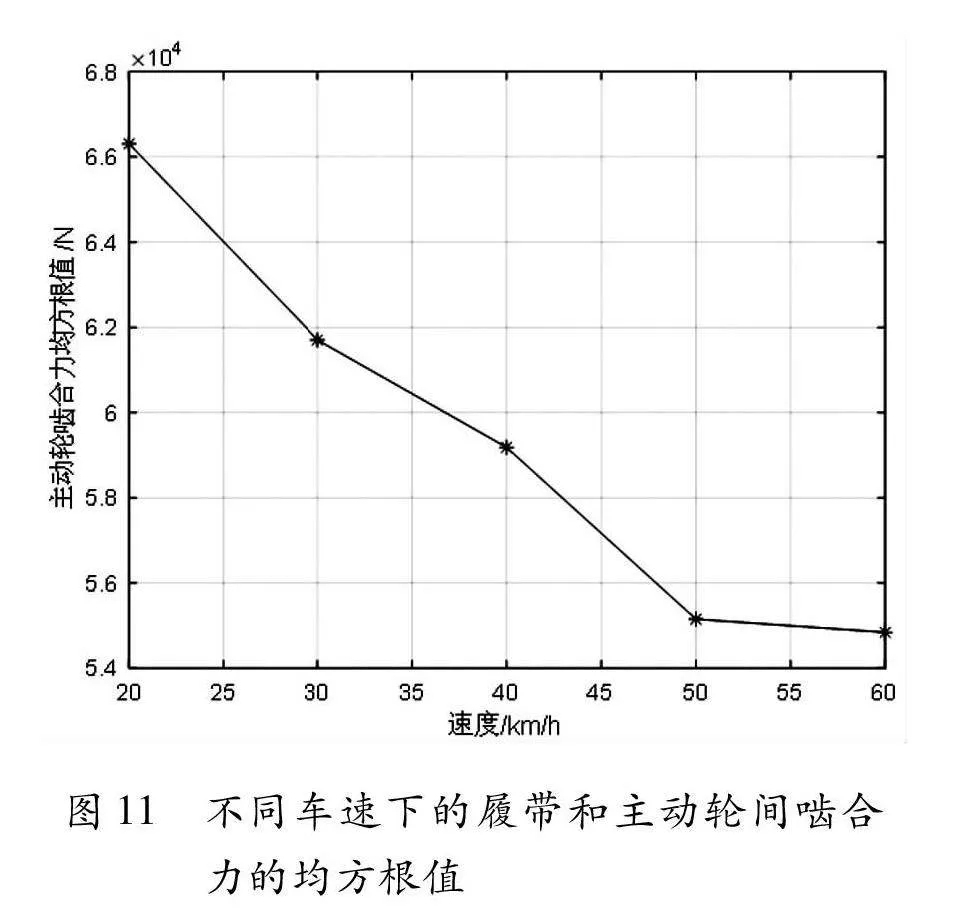
从图10可以看出，不同行驶车速下履带板与主动轮啮合力随着车速的增加，其啮合频次不断增加，啮合力幅值有一定程度的减小。以啮合力变化曲线的有效均方根值（不考虑曲线中的零值）作为评价指标，得到不同车速下某履带板与主动轮之间啮合力有效均方根值变化曲线如图11所示。

从图11中可知，在一定的履带预张紧力情况下，履带板与主动轮间的啮合力随着行驶车速的增加而减小，这与车辆在高速情况下发动机输出的扭矩减少有关。

4.2 不同预紧力对履带行驶啮合稳定性的仿真分析

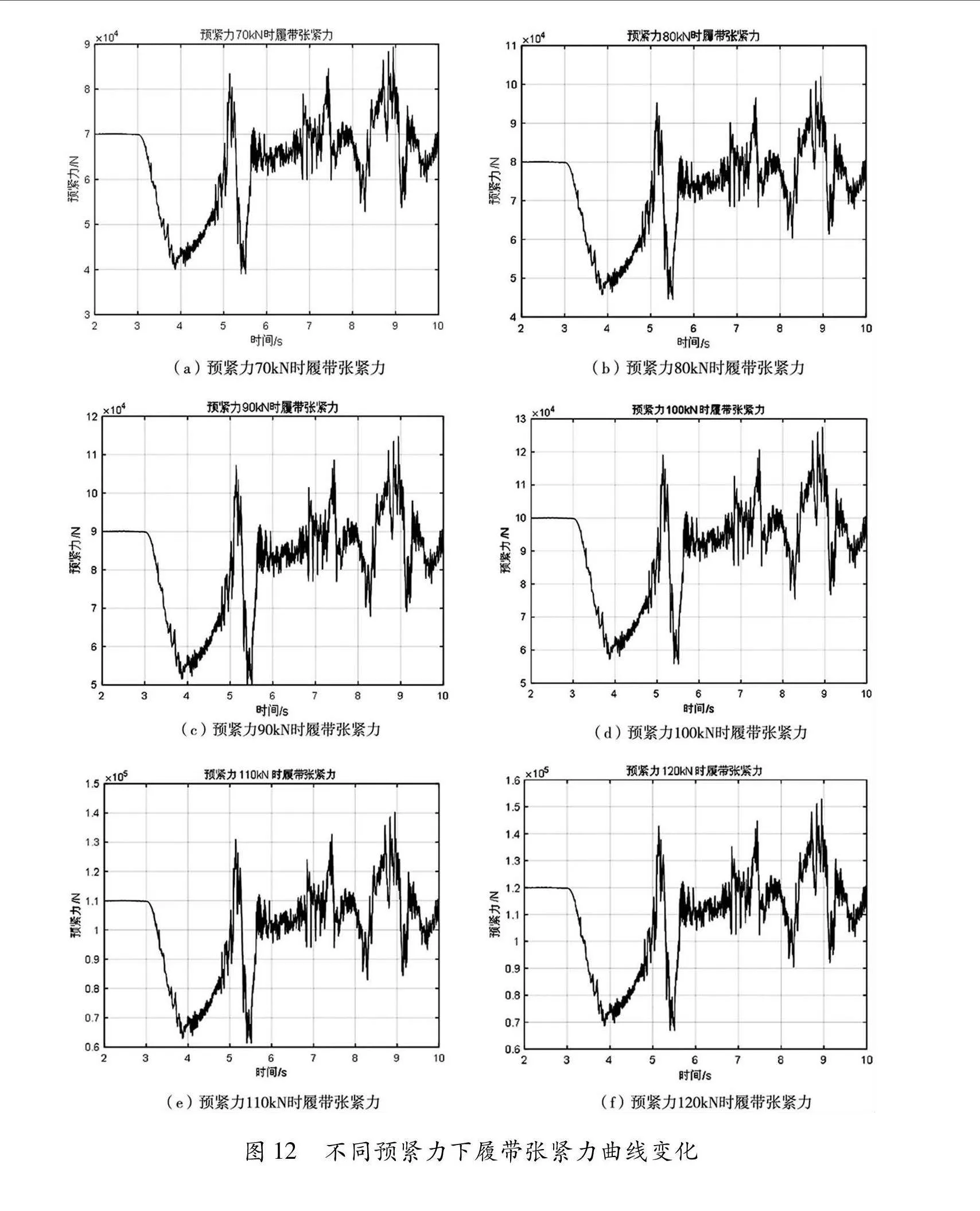
前面对一定预紧力下不同速度对履带行驶啮合稳定性进行了仿真，本节研究一定速度下不同预紧力对履带行驶啮合稳定性的影响。设定重载履带车辆行驶速度一定为30km/h，调整履带车辆行驶系统预张紧力分别为70kN、80kN、90kN、100kN、110kN和120kN，基于前面建立的重载履带车辆整车动力学仿真分析模型分别进行计算分析，以履带行进间张紧力和履带板与主动轮间啮合力作为评价指标，仿真结果如图12所示。

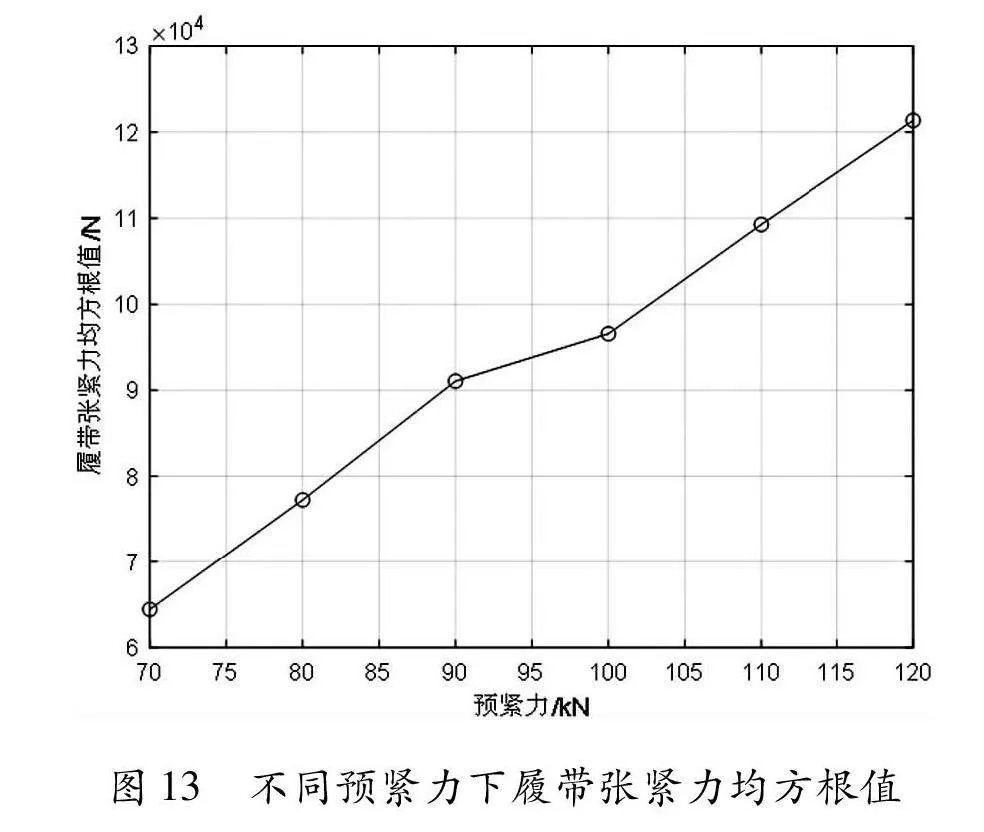
从图12可以看出，履带不同预紧力下实际履带张紧力在车速稳定之后，始终围绕预张紧力上下波动。以在车速稳定后的实际履带张紧力曲线段的均方根值作为评价指标，如图13所示。

从图13可以看出，实际张紧力的均方根值与履带预紧力密切相关，随着预紧力的增大而增大。

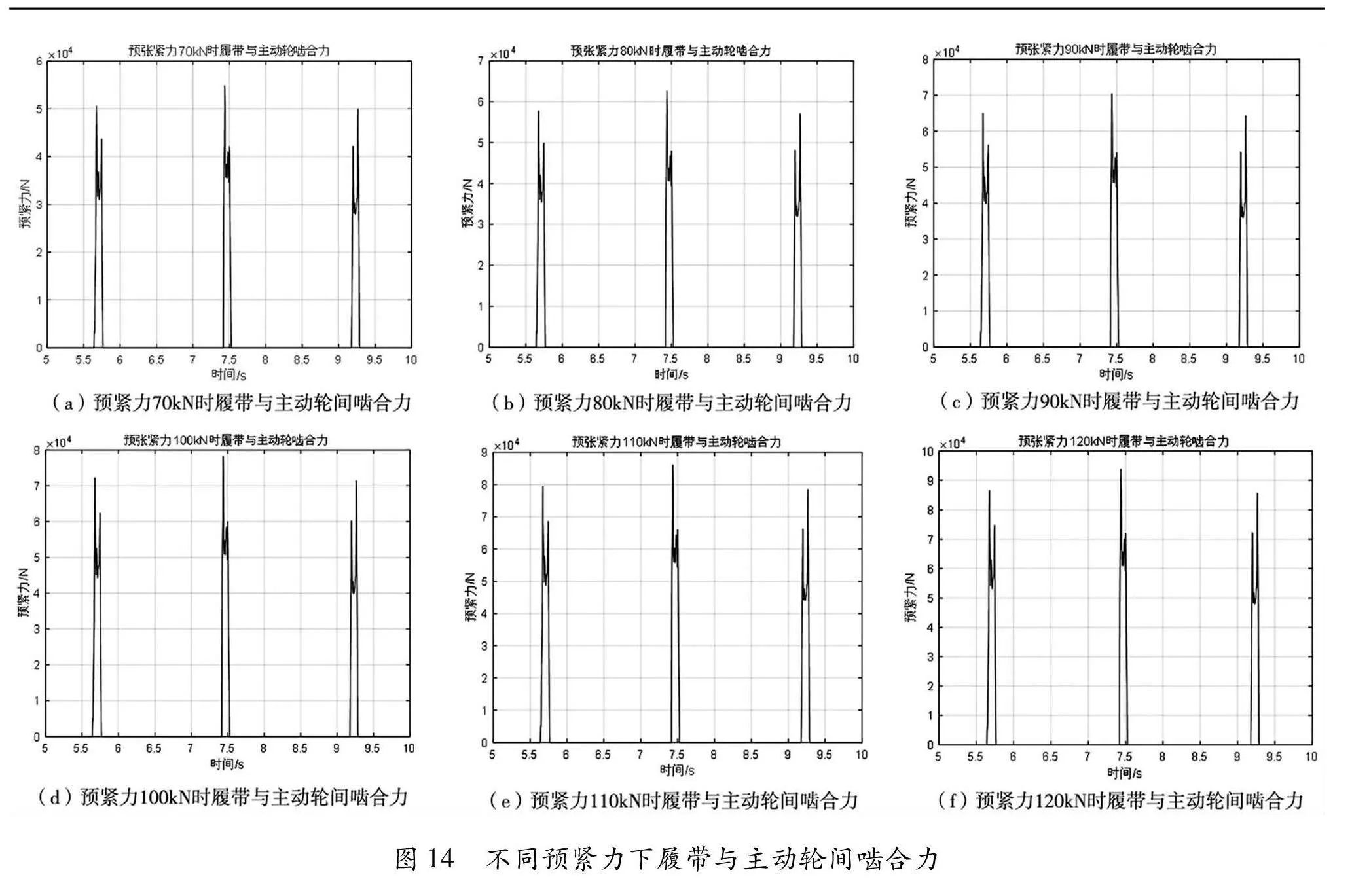
设定车速30km/h时在砂石道路上进行仿真分析，待车速稳定后，得到履带不同预紧力下某履带板与主动轮之间啮合力的变化曲线，如图14所示。

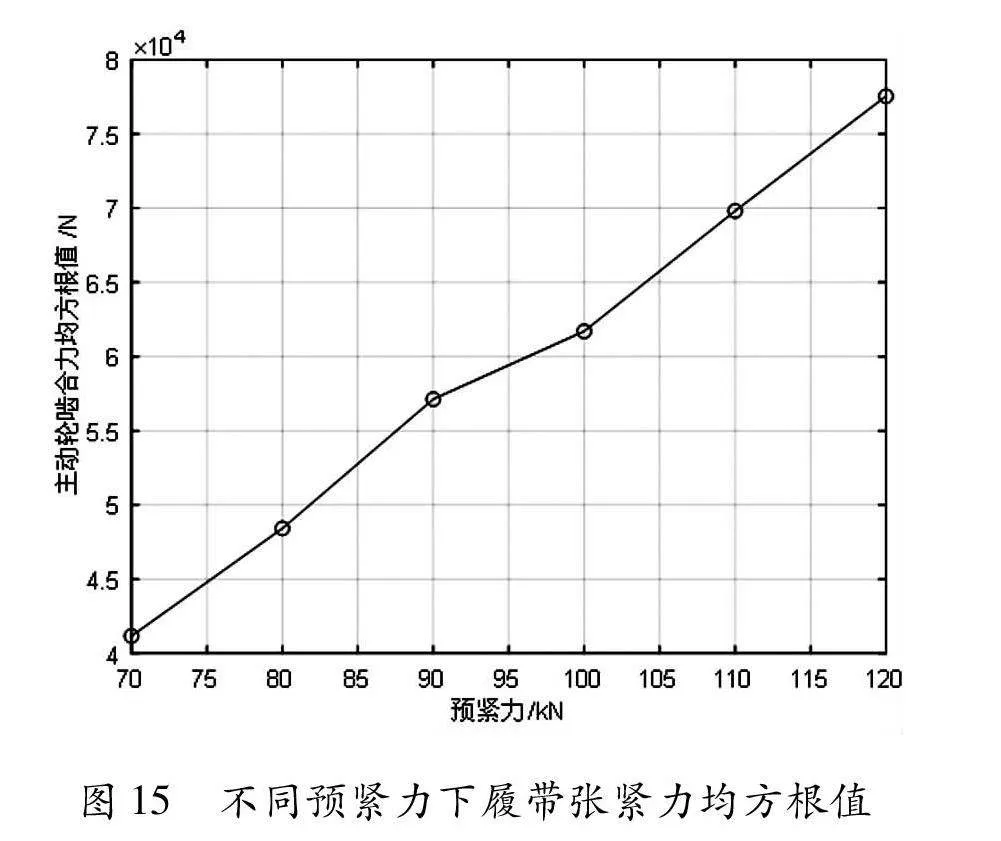
从图14可以看出，给履带设定不同预紧力时，某履带板与主动轮间啮合力在车速确定后，该履带板与主动轮间啮合力出现间隔一致，履带板与主动轮间的啮合力随预紧力的不同而不同。以该履带板与主动轮间啮合力的有效均方根值（不考虑曲线中零值）为评价指标，得到不同预紧力和啮合力之间的关系如图15所示。

从图15可知，履带板与主动轮间的啮合力随着预紧力的增大而增加。

5 结论

履带车辆行驶啮合稳定性主要是指履带与主动轮的啮合匹配特性，主要评价指标为履带啮合力幅

值及统计均方根值，履带张力对履带啮合力的影响等。本文以某重载履带车辆结构布局和参数为依据，基于RecurDyn软件建立了整车行驶系统动力学模型，对行驶系统不同车速和不同预紧力下的履带实际张紧力和履带板与主动轮间的啮合力变化进行了仿真分析，通过分析可知，在履带预紧力一定的情况下，履带的实际动态张紧力随着车速的增加而增加，履带板与主动轮间的啮合力随着行驶车速的增加而减小，这与车辆在高速情况下发动机输出的扭矩减少有关；在履带车辆行驶速度一定的情况下，实际张紧力的均方根值随预紧力的增大而增大，履带板与主动轮间的啮合力也随预紧力的增大而增大。所得结论有助于履带车辆行动系统的优化设计，为进一步完善行动系统推进效率和提高车辆的行驶稳定性奠定了基础。

参考文献：

［1］陈轶杰，张亚峰，徐龙，等.高机动履带车辆动力学建模与悬挂特性优化研究［J］.中国科学.2023（9）：1545-1555.

［2］Mahalingam I，Padmanabhan C.Planar multi-body dynamics of a tracked vehicle using imaginary wheel model for tracks［J］.Defence Sci J，2017（67）：460.

［3］吴锐，于会龙，董昊天，等.履带式特种车辆精细化动力学建模与仿真［J］.兵工学报，2023（7）：1-17.

［4］沁凌云，杨书仪，陈哲吾，等.路面激励下履带车辆负重轮动载荷研究［J］.振动、测试与诊断，2021（4）：652-659.

［5］谢欢，王红岩，郝丙飞，等.履带车辆动力学建模及模型试验验证［J］.农业装备与车辆工程.2018（6）：44-48.

（责任编辑 郭晓勇）